Pochodne 2
Pochodna funkcji odwrotnej
Niech będzie dana w przedziale [math][a,b]\;[/math] funkcja różniczkowalna i różnowartościowa [math]y=f(x)\;[/math]. Wiadomo, że istnieje wówczas funkcja odwrotna [math]f^{-1}\;[/math] (którą oznaczymy tu [math]g\;[/math] : [math]x=g(y)\;[/math] ), ciągła w przedziale [math][f(a), f(b)]\;[/math] (lub [math][f(b), f(a)]\;[/math] — zależnie od tego, czy [math]f\;[/math] jest rosnąca czy malejąca). Pokażemy, że w tym przedziale funkcja [math]g\;[/math] też jest różniczkowalna, a przy okazji wyprowadzimy wzór na pochodną funkcji odwrotnej. Mianowicie mamy
Twierdzenie
Jeśli [math]f(x)=y\;[/math] tzn. [math]x=g(y)\;[/math], to
przy założeniu że [math]f'(x)\ne 0\;[/math].
Dowód
Przy zadanym [math]x\;[/math] weźmy [math]k= f(x+h)-f(x)\;[/math]. Mamy więc [math]f(x+h)=y+k\;[/math], tzn. [math]x+h=g(y+k)\;[/math], skąd [math]h=g(y+k)-g(y)\;[/math]. Możemy więc traktować [math]h\;[/math] jako funkcję [math]k\;[/math]. Ze względu na ciągłość funkcji [math]g\;[/math], mamy [math]\lim_{h \to 0} h(k)=0\;[/math], a ponadto dla [math]k\ne 0\;[/math] mamy [math]h\ne 0\;[/math], ponieważ funkcja [math]g\;[/math] jest różnowartościowa. Mamy więc:
Przy drugiej równości powyżej korzystaliśmy z faktu, iż dla funkcji ciągłych [math]F(x)\;[/math], [math]G(y)\;[/math] mamy: Jeśli [math]y_0 = F(x_0)\;[/math], to [math]\lim_{x\to x_0} G(F(x)) = \displaystyle\mathop{\lim}_{y \to y_0} G(y)\;[/math].
CBDO
Uwaga
Twierdzenie powyższe ma ilustrację/interpretację geometryczną. Rozpatrzmy krzywą daną równaniem [math]y=f(x)\;[/math]. Poprowadźmy w jakimś punkcie [math](x_0,y_0\;[/math] (tu [math]y_0=f(x_0)\;[/math]) styczną do tej krzywej i znaczmy przez [math]\alpha\;[/math] kąt utworzony przez styczną z osią [math]OX\;[/math], a przez [math]\beta;[/math] — kąt utworzony przez styczną z osią [math]OY\;[/math]. Oczywiście [math]\alpha=\frac{\pi}{2}-\beta\;[/math]. Wówczas [math]\tg\; \beta = \ctg\; \alpha\;[/math] czyli [math]\tg\;\beta=\frac{1}{\tg\;\alpha}\;[/math] — zgodnie z wzorem (1). Za pomocą powyższego twierdzenia policzymy pochodne kolejnych funkcji elementarnych.
Twierdzenie
[math](e^x)'=e^x\;[/math] i, ogólniej, [math](a^x)'= a^x \ln a\;[/math].
Dowód
Weźmy [math]y=f(x)=e^x\;[/math] ; wtedy [math]x=f^{-1}(y)\equiv g(y)=\ln y\;[/math]. Mamy: [math]g'(y)=\frac{1}{y}=\frac{1}{e^x}=\frac{1}{f'(x)}\;[/math], a ostatnia równość to właśnie [math]f'(x)=(e^x)' =e^x\;[/math].
W ogólniejszym przypadku [math](a^x)'\;[/math], bierzemy [math]y=f(x)=a^x\;[/math], a dla funkcji odwrotnej [math]x=g(y)=\log_a y\;[/math]. Pamiętamy, że [math]g'(y)=\frac{1}{y\ln a}=\frac{1}{f'(x)}\Longrightarrow f'(x)=a^x\ln a\;[/math].
CBDO
Twierdzenie
- [math](\arcsin x)'=\frac{1}{\sqrt{1-x^2}}\;[/math]
- [math](\arccos x)'=-\frac{1}{\sqrt{1-x^2}}\;[/math].
Dowód
- Weźmy [math]y=f(x)=\arcsin x\;[/math] i wtedy [math]x=g(y)=\sin\; y\;[/math]. Mamy: [math]g'(y)=\cos\; y =\sqrt{1-\sin\;^2 y}=\sqrt{1-x^2}=\frac{1}{f'(x)}\;[/math], (znak pierwiastka to plus, bo [math]x\in[-\frac{\pi}{2},+\frac{\pi}{2}]\;[/math] ), a ostatnia równość to [math]f'(x)=(\arcsin x)'= \frac{1}{\sqrt{1-x^2}}\;[/math].
- Rozważania są analogiczne: [math]y=f(x)=\arccos x\;[/math], [math]x=g(y)= \cos\; y\;[/math] ; jedyna różnica jest w znaku, bo [math]g'(y)=-\sin\; y\;[/math] i dalej jak w a), z wynikiem końcowym [math](\arccos x)'=-\frac{1}{\sqrt{1-x^2}}\;[/math].
CBDO
Twierdzenie
[math](arctg x)' = \frac{1}{1+x^2}\;[/math].
Dowód
Dla [math]y=f(x)=arctg x\;[/math] jest [math]x=g(y)=\tg\; y\;[/math], [math]g'(y)=\frac{1}{\cos\;^2 y}\;[/math] ; stąd [math]f'(x)=\cos\;^2 y=\frac{1}{1+\tg\;^2 y}=\frac{1}{1+(\tg\;(arctg(x))^2}= \frac{1}{1+x^2}\;[/math].
Ekstrema funkcji. Twierdzenie Rolle'a
Maksimum i minimum
Niech funkcja [math]f\;[/math] będzie określona w otoczeniu punktu [math]a\;[/math] (tzn. w jakimś przedziale otwartym, zawierającym [math]a\;[/math] ). Jeśli istnieje takie [math]\delta\gt 0\;[/math], że
to mówimy, że funkcja [math]f(x)\;[/math] ma maksimum w punkcie [math]a\;[/math]. Jeśli zaś przy analogicznych założeniach mamy nierówność:
to mówimy, że funkcja [math]f(x)\;[/math] ma minimum w punkcie [math]a\;[/math].
Innymi słowy, w punkcie [math]a\;[/math] występuje maksimum (minimum), jeśli istnieje takie otoczenie [math]U\;[/math] punktu [math]a\;[/math], że [math]f(a)\;[/math] jest największą (najmniejszą) liczbą w zbiorze wartości, jakie funkcja [math]f\;[/math] przyjmuje na [math]U\;[/math].
Jeśli we wzorach (2) i (3) zastąpić znaki [math]\geq\;[/math] ([math]\leq\;[/math] ) przez [math]\gt \;[/math] ([math]\lt \;[/math] ), to mamy do czynienia z maksimum (minimum) właściwym.
Przykłady
- Funkcja [math]x^2\;[/math] posiada minimum w punkcie [math]x=0\;[/math] ;
- funkcja [math]\cos\; x\;[/math] posiada maksima w punktach [math]2 k \pi\;[/math], [math]k\in \mathbb Z \; \;[/math] oraz minima w punktach [math](2k+1)\pi\;[/math], [math]k\in \mathbb Z \; \;[/math].
- funkcja [math]|x|\;[/math] posiada minimum w [math]x=0\;[/math].
Esktrema
Maksima i minima obejmujemy wspólną nazwą ekstremów funkcji [math]f\;[/math]. Z pojęciem ekstremum ściśle jest związane (ale różne) pojęcie kresów wartości funkcji na zbiorze. Ekstrema są pojęciami lokalnymi: Aby stwierdzić, czy funkcja posiada ekstremum w danym punkcie [math]a\;[/math], wystarczy znać wartości funkcji w dowolnie małym otoczeniu punktu [math]a\;[/math]. Natomiast wyznaczenie kresów zbioru wartości funkcji na zbiorze [math]X\;[/math] wymaga znajomości funkcji na całym [math]X\;[/math].
Z definicji maksimum wynika natychmiast
Twierdzenie
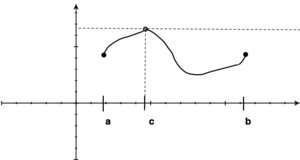
Jeśli funkcja [math]f\;[/math] określona w przedziale [math][a,b]\;[/math] osiąga kres górny w punkcie [math]c\;[/math] należącym do wnętrza tego przedziału (tzn. [math]a\lt c\lt b\;[/math] ), to funkcja posiada maksimum w [math]c\;[/math]. (analogicznie dla kresu dolnego i minimum).
CBDO
Kresy
Jeśli okaże się, że kres górny funkcji jest osiągany w jednym z końców przedziału [math][a,b]\;[/math] (np. w [math]a\;[/math] ), to nie mówimy, iż w tym punkcie funkcja posiada maksimum, ponieważ funkcja nie jest określona w otoczeniu [math]a\;[/math]. Np. funkcja [math]y=x\;[/math] na zbiorze [math]X=[0,1]\;[/math] posiada kres górny równy 1; nie nazywamy go jednak maksimum.
Twierdzenie
Jeśli funkcja [math]f\;[/math] jest różniczkowalna w punkcie [math]c\;[/math] i posiada w tym punkcie ekstremum, to [math]f'(c)=0\;[/math].
Dowód
Załóżmy, że [math]f\;[/math] posiada w punkcie [math]c\;[/math] maksimum (jeśli minimum, to rozumowanie jest analogiczne). Weźmy więc takie [math]\delta\gt 0\;[/math], aby dla dowolnego [math]h\;[/math] takiego, że[math]|h|\lt \delta\;[/math], zachodziła nierówność [math]f(c+h)-f(c)\leq 0\;[/math]. Dzieląc przez [math]h\;[/math], otrzymujemy
Ponieważ z założenia istnieje pochodna [math]f'(c)\;[/math], to
Z poprzednich nierówności wynika jednak, że [math]f'_+(c)\leq 0\leq f'_-(c)\;[/math]. Musi więc być
CBDO
Uwaga
Twierdzenie odwrotne nie zachodzi: Równość [math]f'(c)=0\;[/math] może być spełniona, mimo iż funkcja [math]f\;[/math] nie posiada ekstremum w [math]c\;[/math]. Jest tak np. dla funkcji [math]f(x)=x^3\;[/math] w punkcie [math]x=0\;[/math].
Punkt krytyczny
Jeśli funkcja jest różniczkowalna w [math]x=a\;[/math] i [math]f'(a)=0\;[/math], to punkt [math]x=a\;[/math] nazywamy punktem krytycznym funkcji [math]f\;[/math].
Uwaga
Istnienie ekstremum funkcji różniczkowalnej w punkcie [math]c\;[/math] oznacza, że styczna do krzywej [math]y=f(x)\;[/math] w punkcie [math](c,f(c)\;[/math] jest równoległa do osi [math]OX\;[/math] (z możliwością, że się z tą osią pokrywa).
Twierdzenie (Rolle'a)
Niech funkcja [math]f\;[/math] będzie ciągła w przedziale domkniętym [math][a,b]\;[/math] i różniczkowalna wewnątrz tego przedziału. Jeśli [math]f(a)=f(b)\;[/math], to istnieje takie [math]c\;[/math], że [math]a\lt c\lt b\;[/math] oraz [math]f'(c)=0\;[/math].
Dowód
Jeśli funkcja [math]f\;[/math] jest stała, to [math]\forall_{x\in[a,b]} f'(x)=0\;[/math]. Można wtedy wziąć dowolny [math]x\in]a,b[\;[/math] i teza tw. Rolle'a będzie spełniona.
Załóżmy więc, że funkcja [math]f\;[/math] nie jest stała; np. niech przyjmuje wartości większe od [math]f(a)\;[/math]. Oznaczając przez [math]M\;[/math] kres górny zbioru wartości funkcji na przedziale [math][a,b]\;[/math], mamy: [math]M\gt f(a)\;[/math]. Zatem, z tw. Weierstrassa, istnieje takie [math]c\in[a,b]\;[/math], że [math]f(c)=M\;[/math]. Przy tym [math]a\ne c\ne b\;[/math], ponieważ z założenia [math]f(a)=f(b)\;[/math] ; zatem [math]a\lt c\lt b\;[/math]. To znaczy, że funkcja [math]f\;[/math] osiąga kres górny w punkcjie [math]c\;[/math] położonym wewnątrz przedziału [math][a,b]\;[/math]. Zgodnie z twierdzeniem niedawno udowodnionym funkcja [math]f\;[/math] posiada w punkcie [math]c\;[/math] maksimum, co z kolei implikuje (pamiętając o różniczkowalności [math]f\;[/math] wewnątrz przedziału), że [math]f'(c)=0\;[/math].
CBDO
Uwaga
Twierdzenie Rolle'a można sformułować w następujący sposób:
Jeśli [math]f(x)=f(x+h)\;[/math], to istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że
przy tych samych założeniach, tzn. funkcja [math]f\;[/math] ma być różniczkowalna wewnątrz przedziału [math][x,x+h]\;[/math] (lub [math][x+h,x]\;[/math], jeśli [math]h\lt 0\;[/math] ; nie zakładamy tu, że [math]h\gt 0\;[/math] lecz jedynie że [math]h\ne 0\;[/math] ) i ciągła w [math]x\;[/math] oraz [math]x+h\;[/math].
Twierdzenie Lagrange'a i Cauchy'ego
Twierdzenie (Lagrange'a)
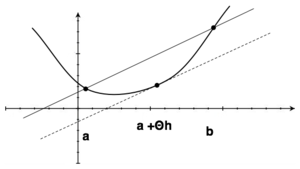
Załóżmy (podobnie jak w tw. Rolle'a), że funkcja [math]f\;[/math] jest ciągła w przedziale [math][a,b]\;[/math] i różniczkowalna wewnątrz tego przedziału. Zachodzi wówczas wzór
gdzie [math]h=b-a\;[/math] oraz [math]\theta\in]0,1[\;[/math].
Uwaga
Wzór ten nazywany jest też wzorem Lagrange'a na wartość średnią, lub twierdzeniem o przyrostach skończonych. Widać, że szczególnym przypadkiem (gdy [math]f(a)=f(b)\;[/math] ) jest tw. Rolle'a. Okazuje się, że dowód tw. Lagrange'a można sprowadzić do tw. Rolle'a.
Dowód
Weźmy mianowicie funkcję [math] g(x)=f(a)-f(x)+(x-a)\frac{f(b)-f(a)}{b-a} \;[/math] i ponadto [math]g(x)\;[/math] jest ciągła na [math][a,b]\;[/math] i różniczkowalna w [math]]a,b[\;[/math] ; jej pochodna jest
Ponadto [math]g(b)=0=g(a)\;[/math], zatem [math]g(x)\;[/math] spełnia założenia tw. Rolle'a. Skoro tak, to pochodna [math]g'(x)\;[/math] znika w pewnym punkcie między [math]a\;[/math] i [math]b\;[/math]. Możemy to wypowiedzieć tak, że istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że
czyli zachodzi wzór z tezy tw. Lagrange'a.
CBDO
Uwaga
W sposób podobny, jak wzór (4) przy tw. Rolle'a, można tezę tw. Lagrange'a sformułować w następujący sposób:
Dla funkcji [math]f\;[/math] różniczkowalnej wewnątrz przedziału [math][x,x+h]\;[/math] i ciągłej na [math][x,x+h]\;[/math] (to dla [math]h\gt 0\;[/math] ; dla [math]h\lt 0\;[/math] jest to przedział [math][x+h,x]\;[/math] ) istnieje takie [math]\theta: 0\lt \theta\lt 1\;[/math], że
Wnioski wypływające z twierdzenia Lagrange'a
Z tw. Lagrange'a wypływają dwa wnioski, bardzo ważne dla rachunku całkowego:
Twierdzenie
Jeśli [math]\forall_{x\in ]a,b[}\;[/math] zachodzi [math]f'(x)=0\;[/math], to funkcja w tym przedziale jest stała.
Dowód
Na mocy udowodnionego dopiero co wzoru (6), mamy bowiem dla każdego [math]x\;[/math] i [math]h\;[/math]: [math]f(x)=f(x+h)\;[/math], co oznacza, że [math]f(x)=\;[/math] const.
CBDO
Twierdzenie
Jeśli [math]\forall_{x\in ]a,b[}\;[/math] zachodzi [math]f'(x)=g'(x)\;[/math], to [math]f(x)=g(x)+\;[/math] const.
Dowód
Mamy: [math](f(x)-g(x))'= f'(x)-g'(x)=0\;[/math], czyli funkcja [math]f(x)-g(x)\;[/math] ma pochodną równą zeru. Na mocy dopiero co udowodnionego twierdzenia znaczy to, że [math]f(x)-g(x)\;[/math] jest stała, tzn. [math]f(x)=g(x)+\;[/math] const.
CBDO
Twierdzenie (Cauchy'ego; (czasem z przydomkiem: O wartości średniej))
Jeśli funkcje [math]f\;[/math] i [math]g\;[/math] są ciągłe na przedziale [math][a,b]\;[/math] i różniczkowalne wewnątrz oraz jeśli [math]\forall_{x\in ]a,b[}\;[/math] jest [math]g'(x)\ne 0\;[/math], to istnieje takie [math]\theta\in]0,1[\;[/math], że
gdzie [math]h=b-a\;[/math].
Przed dowodem
Uwaga
Twierdzenie Lagrange'a otrzymuje się z tw. Cauchy'ego, jeśli podstawić [math]g(x)=x\;[/math]. Okazuje się, że także tw. Cauchy'ego wynika z tw. Lagrange'a, ale tu trzeba zaargumentować następująco:
Dowód
Weżmy funkcję
(mianownik [math]g(b)-g(a)\;[/math] jest różny od zera ze względu na założenie, że wszędzie w przedziale [math]]a,b[\;[/math] mamy [math]g'(x)\ne 0\;[/math] i tw. Rolle'a).
Funkcja [math]G(x)\;[/math] spełnia założenia tw. Rolle'a: Jest różniczkowalna i ciągła jak trzeba, oraz [math]G(a)=0=G(b)\;[/math]. Pochodna funkcji [math]G(x)\;[/math] jest
zatem (z tw. Rolle'a) istnieje takie [math]\theta\in]a,b[\;[/math], że [math]G'(a+\theta h)=0\;[/math]. Podstawiając [math]x=a+\theta h\;[/math] we wzorze (8), otrzymujemy (7).
Analogicznie do sposobu, w jaki tw. Rolle'a i Lagrange'a były wyrażane wzorami (4) i (6), można tw. Cauchy'ego sformułować tak: Istnieje [math]\theta\in]0,1[\;[/math] takie, że
Uwaga
W powyższym wzorze [math]\theta\;[/math] jest TO SAMO w liczniku i mianowniku.
Różniczkowanie funkcji złożonych
Niech [math]y=f(x)\;[/math], [math]z=g(y)\;[/math], przy tym funkcja [math]g\;[/math] jest określona na zbiorze wartości funkcji [math]f\;[/math] ; ponadto niech [math]f\;[/math] i [math]g\;[/math] będą różniczkowalne, a pochodna [math]g'\;[/math] niech będzie ciągła. Następujący wzór wyraża pochodną funkcji złożonej [math]g(f(x))\;[/math] przez pochodne [math]f'\;[/math] i [math]g'\;[/math].
Twierdzenie
Dowód
Przy danych [math]x\;[/math] i [math]h\ne 0\;[/math] weźmy [math]k=f(x+h)-f(x)\;[/math], tzn. [math]f(x+h)=y+k\;[/math]. Zastosujmy teraz wzór Lagrange'a na wartość średnią w wersji (6) do funkcji [math]g\;[/math] ; otrzymamy
dla pewnego [math]\theta \in ]0,1[\;[/math] (pamiętajmy, że [math]\theta\;[/math] jest pewną funkcją [math]h\;[/math] ). Co stanie się z powyższym wyrażeniem, gdy weźmiemy jego granicę przy [math]h\to 0\;[/math]? Otóż ze względu na ciągłość funkcji [math]g\;[/math], mamy [math]\displaystyle\mathop{\lim}_{h\to 0} k =0\;[/math], a ponieważ [math]0\lt \theta\lt 1\;[/math], to również [math] \displaystyle\mathop{\lim}_{h\to 0} \theta k =0\;[/math]. Skoro tak, to [math]\displaystyle\mathop{\lim}_{h\to 0} (y+\theta k)=y\;[/math], co — w połączeniu z ciągłością funkcji [math]g'\;[/math] — daje
Mamy więc:
Przykłady
- [math](\sin\;^2 x)'\;[/math] na dwa sposoby:
- [math](\sin^2(x))'=(\sin(x) \sin(x))'=\sin(x) \cos(x) + \cos(x) \sin(x) = 2\sin(x) \cos(x) \;[/math]
- (różniczkowanie funkcji złożonej) [math](\sin^2(x))' = (\sin(x))' 2(\sin(x)) = 2\sin(x) \cos(x)\;[/math]
- [math](e^{\sin(x)})'=(\sin(x))'e^{\sin(x)} = \cos(x) e^{\sin(x)}\;[/math]
- Udowodnimy teraz anonsowany wcześniej wzór
[math] (x^a)'=a x^{a-1}\;\;\;{\rm dla}\;\;\; a\in\mathbb R \; . \;[/math] Dow. Napiszmy [math]x^a\;[/math] w postaci: [math]x^a=e^{a\ln x}\;[/math] i ze wzoru na pochodną funkcji złożonej
[math] (x^a)'=(e^{a\ln x})' =\frac{d e^{a\ln x}}{d x}=\frac{d a \ln x}{d x} \cdot \left. \frac{d e^y}{d y}\right|_{y=a\ln x}=a\frac{1}{x} e^y|_{y=a\ln x}= a x^{-1}x^a =a x^{a-1} [/math] CBDO
Niejednokrotnie trzeba kilkakrotnie zastosować twierdzenie o pochodnej funkcji złożonej. Mamy np. pochodną funkcji trzykrotnie złożonej:
Sztuczka mnemoteczniczna
Wzór powyższy można zapamiętać np. w następujący sposób:
Oznaczmy: [math]y=f(x)\;[/math], [math]z=g(y)\;[/math], [math]w=h(z)\;[/math], oraz [math]W(x)=h(g(f(x)))\;[/math]. Można wtedy napisać
pamiętając,w jakich punktach są liczone wszystkie pochodne.
W powyższym wzorze pochodne zachowują się jak ułamki. Ale UWAGA! Jest to zbieżność przypadkowa; inne pochodne (zwł. cząstkowe) już siętak nie zachowują!
Uwaga — wzór na pochodną funkcji odwrotnej
ze wzoru na pochodną funkcji złożonej: [math]f^{-1}(f(x))=x,\;[/math] biorąc pochodną: [math]f'(x)(f^{-1})' (f(x))'=1\;[/math] i [math](f^{-1})'(f(x))=\frac{1}{f'(x)}[/math] lub [math](f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))}\;[/math]
Związek między znakiem pochodnej a monotonicznością funkcji
Z tw. Lagrange'a wynika następujący związek pomiędzy znakiem pochodnej a tym, czy funkcja rośnie, czy maleje.
Twierdzenie *
Jeśli [math]\forall_{x\in [a,b]}\;[/math] zachodzi nierówność [math]f'(x)\gt 0\;[/math], to funkcja [math]f\;[/math] jest w tym przedziale ściśle rosnąca. Jeśli mamy [math]f'(x)\lt 0\;[/math], to funkcja [math]f\;[/math] jest ściśle malejąca.
Dowód
Ze wzoru (6) mamy, dla [math]h\gt 0\;[/math] : [math]f(x+h)\gt f(x)\;[/math] jeśli w przedziale [math][x,x+h]\;[/math] pochodna jest stale dodatnia, bądź [math]f(x+h)\lt f(x)\;[/math], jeśli pochodna jest stale ujemna. Czyli funkcja jest ściśle rosnąca w pierwszym przypadku, a ściśle malejąca w drugim.
CBDO
Uwaga
Jeśli założyć, że zachodzi nierówność nieostra [math]f'(x)\geq 0\;[/math] ([math]f'(x)\leq 0\;[/math] ), to w tezie mamy, że funkcja jest rosnąca (malejąca).
Zachodzi również twierdzenie odwrotne do powyższego:
Twierdzenie
Jeśli funkcja [math]f\;[/math] jest różniczkowalna w punkcie [math]c\;[/math] i rośnie (maleje) w jakimś przedziale [math]]a,b[\;[/math] zawierającym ten punkt, to [math]f'(c)\geq 0\;[/math] (odpowiednio [math]f'(c)\leq 0\;[/math] ).
Dowód
Jeśli [math]f\;[/math] rośnie, to dla [math]h\gt 0\;[/math] mamy
i przechodząc do granicy [math]\displaystyle\mathop{\lim}_{h\to 0}\;[/math] otrzymujemy [math]f'(c)\geq 0\;[/math].
Jeśli funkcja [math]f\;[/math] maleje, to rozumowanie jest analogiczne.
CBDO
Z tw. *(https://brain.fuw.edu.pl/edu/Matematyka:Pochodne1#Twierdzenie_.2A) wynika
Twierdzenie (wynikające z tw. *)
Jeśli [math]f'(c)\gt 0\;[/math] i pochodna [math]f'(x)\;[/math] jest ciągła w punkcie [math]c\;[/math], to funkcja [math]f\;[/math] jest ściśle rosnąca w pewnym otoczeniu punktu [math]c\;[/math].
Analogicznie: Jeśli [math]f'(c)\lt 0\;[/math] i pochodna [math]f'(x)\;[/math] jest ciągła w punkcie [math]c\;[/math],to funkcja [math]f\;[/math] jest ściśle malejąca w pewnym otoczeniu punktu [math]c\;[/math].
Dowód
Ponieważ funkcja [math]f'(x)\;[/math] jest ciągła w [math]c\;[/math], to nierówność [math]f'(c)\gt 0\;[/math] mówi, że w pewnym otoczeniu punktu [math]c\;[/math] funkcja [math]f'(x)\;[/math] jest dodatnia: [math]\exists_{\delta\gt 0}: \forall_{h\lt \delta}: f'(c+h)\gt 0\;[/math]. Znaczy to, że pochodna [math]f'\;[/math] jest dodatnia [math]\forall_x: c-h\lt x\lt c+h\;[/math]. Na mocy https://brain.fuw.edu.pl/edu/Matematyka:Pochodne1#Twierdzenie_.2A, funkcja [math]f\;[/math] jest rosnąca w tym przedziale.
CBDO
Uwaga
Powyższe twierdzenie można przeformułować w następujący sposób:
- Jeśli [math]f'(c)\ne 0\;[/math], to (przy założeniu ciągłości pochodnej) funkcja [math]f\;[/math] jest różnowartościowa w pewnym otoczeniu punktu [math]c\;[/math], tzn. dla [math]]c-\delta, c+\delta[\;[/math] ([math]\delta \gt 0\;[/math] ). Skoro tak, to funkcja [math]f\;[/math] posiada w tym przedziale funkcję odwrotną [math]x=g(y)\;[/math], czyli równanie: [math]y=f(x)\;[/math] posiada w tym przedziale dokładnie jedno rozwiązanie..
- Jak wiemy, pochodna tejże funkcji odwrotnej [math]g'(y)\;[/math] jest odwrotnością pochodnej funkcji [math]f'(x)\;[/math].
- Powyższe fakty: Przy założeniu [math]f'(c)\ne 0\;[/math] istnieje w otoczeniu punktu [math]f(c) \;[/math] funkcja odwrotna, lub że równanie: [math]y=f(x)\;[/math] ma dokładnie jedno rozwiązanie w otoczeniu punktu [math]c\;[/math] — przenoszą się na wyższe wymiary, tzn. zachodzą dla odwzorowań [math]\mathbb R \; ^n \to \mathbb R \; ^n\;[/math]. Oczywiście konieczne jest stosowne uogólnienie pojęć. Będzie o tym mowa w semestrze II.
Wyrażenia nieoznaczone i reguła de l'Hospitala
Często zdarza się konieczność obliczania granic postaci następującej: [math]\displaystyle\mathop{\lim}_{x\to a} \frac{f(x)}{g(x)}, \;\;\;\; {\rm gdzie}\;\;\; f(a)=0=g(a).\;[/math] Wyrażenia tego rodzaju noszą nazwę wyrażeń nieoznaczonych typu [math]\frac{0}{0}\;[/math].
Twierdzenie
Jeśli funkcje [math]f\;[/math] i [math]g\;[/math] są ciągłe w przedziale domkniętym [math][a,b]\;[/math] i są różniczkowalne wewnątrz tego przedziału i jeśli [math]f(a)=0=g(a)\;[/math], to
przy założeniu, że ta ostatnia granica istnieje.
Dowód
Kluczem do dowodu jest twierdzenie Cauchy'ego o wartości średniej.
Oznaczmy: [math]x=a+h\;[/math]. Należy dowieść, że [math] \lim_{h\to 0^+} \frac{f(a+h)}{g(a+h)} =\lim_{h \to 0^+} \frac{f'(a+h)}{g'(a+h)}.\;[/math] Ale: Równości: [math]f(a)=0=g(a)\;[/math] i wzór Cauchy'ego (7) dają:
dla pewnego [math]\theta\in]0,1[\;[/math].
Oznaczmy [math]F(x)=\frac{f'(x)}{g'(x)}\;[/math]. Z założenia [math]\displaystyle\mathop{\lim}_{h\to 0^+} F(a+h)\;[/math] istnieje.
Ponieważ zaś [math]\displaystyle\mathop{\lim}_{h\to 0^+} x= 0 \;[/math], to też [math]\displaystyle\mathop{\lim}_{h\to 0^+} x\theta= 0 \;[/math] i, co za tym idzie, [math]\displaystyle\mathop{\lim}_{x\to 0^+} F(a+\theta h)\;[/math] też istnieje i jest równe [math]\displaystyle\mathop{\lim}_{x\to 0^+} F(a+ h)\;[/math]; mamy więc
skąd otrzymujemy wzór (de l'Hospitala).
CBDO
Analogiczne twierdzenie mamy w przypadku granicy lewostronnej.
Wzór de l'Hospitala
W przypadku, gdy pochodne [math]f'\;[/math] i [math]g'\;[/math] są ciągłe w punkcie [math]a\;[/math], a ponadto [math]g'(a)\ne 0\;[/math], ze wzoru (10) (plus jego odpowiednika dla granicy lewostronnej) natychmiast wynika wzór de l'Hospitala:
Uwaga
Po prawej stronie powyższego wzoru nie ma granicy!
Analogiczne wzory mamy w przypadku granic jednostronnych i pochodnych jednostronnych.
Przykład
Uwaga
Jeśli zdarzy się, że po prawej stronie wyrażenia (12) mamy [math]f'(a)=g'(a)=0\;[/math], to tegoż wzoru nie daje się stosować. Ale można postępować rekurencyjnie! tzn. badać wyższe pochodne.
Uwaga
Powyższe twierdzenia dotyczyły wyrażeń typu [math]\frac{0}{0}\;[/math]. Przez sztuczki z zamianą zmiennych i inne, można też liczyć inne wyrażenia nieoznaczone: [math]\frac{\infty}{\infty}\;[/math] ; [math]\infty-\infty\;[/math] ; [math]1^\infty\;[/math] ; [math]0^0\;[/math] ; [math]\infty^0\;[/math].