Fizyka I OO/Wykład XIII

Prawo Ohma

Natężenie prądu płynącego przez przewodnik jest wprost proporcjonalne do napięcia przyłożonego do jego końców.

[math]I=\frac{U}{R}[/math]

Współczynnikiem proporcjonalności pomiędzy tymi wielkościami jest odwrotność oporu elektrycznego.

Opór elektryczny

jest wielkością charakteryzującą przewodnik, zależy od jego rozmiarów, materiału, z jakiego jest wykonany i temperatury. Dla przewodnika o długości l, polu przekroju S, wielkość oporu oblicza się, korzystając z zależności:

[math]R=\rho \frac{l}{S}[/math]

gdzie [math]\rho[/math] jest oporem właściwym przewodnika — wielkość ta zależy od temperatury.

Prawa Kirchoffa

I prawo

Suma prądów wpływających do węzła obwodu elektrycznego jest równa sumie prądów wypływających.

II prawo

Suma sił elektromotorycznych w prostym obwodzie jest równa sumie napięć na poszczególnych opornikach.

Szczególny przypadek II prawa Kirchhoffa

[math] \frac{I_1}{I_2}= \frac{R_2}{R_1}[/math]

Łączenie oporników z prądem

Równoległe

[math]\frac 1 R = \frac 1 {R_1} +\frac 1 {R_2} +\frac 1 {R_3}[/math]

Szeregowe

[math] R = R_1+R_2+R_3[/math]

Gdy łączy się równolegle n jednakowych ogniw o sile elektromotorycznej E i oporze wewnętrznym r_w, opór wewnętrzny n-krotnie maleje, a siła elektromotoryczna nie zmienia się. Natomiast połączenie szeregowe takich samych ogniw powoduje, że siła elektromotoryczna i opór baterii jest wówczas n-krotnie większy niż pojedynczego ogniwa.

Prąd

Metale są dobrymi przewodnikami prądu. Tę cechę zawdzięczają budowie wewnętrznej. Ich atomy tworzą regularną, uporządkowaną strukturę, w której można wyróżnić elementy symetrii. Ich regularne ułożenie przypomina sieć i dlatego nazywa się ją siecią krystaliczną. Elektrony najbardziej zewnętrznych powłok atomowych są luźno związane z atomami; można powiedzieć, że tworzą rodzaj kleju wypełniającego przestrzeń. Tak więc stwierdzenie, że atomy tworzą sieć krystaliczną, nie jest bardzo ścisłe. Należałoby raczej powiedzieć, że tworzą ją jony. Kryształ metalu jest oczywiście elektrycznie obojętny. Jony sieci krystalicznej poruszają się ruchem drgającym wokół położenia równo­wagi. Z drgającym ruchem wiąże się energia. Im większa jest amplituda tych drgań, mówiąc prościej, im większe są te drgania, tym większa jest energia wewnętrzna metalu. Przypomnę Ci, że energia wewnętrzna ciała jest sumą wszystkich energii atomów i cząsteczek tego ciała, a temperatura jest wielkością fizyczną, która zależy od średniej energii kinetycznej ruchu cząsteczek. Jeśli energia kinetyczna się zwiększy, to wskaźnikiem będzie wzrost temperatury.

Jeśli końce opornika połączymy z biegunami źródła napięcia, to w oporniku powstanie pole elektryczne. Pole to natychmiast zmusza swobodne elektrony do wędrówki w kierunku dodatniego potencjału. Nie jest to jednak łatwa droga. Elektrony napotykają drgające jony i zderzają się z nimi. Zderzają się także między sobą. Wobec tego ruch elektronów wzdłuż przewodnika jest bardzo powolny. Chwilami jest przyspieszony, chwilami opóźniony, elektron przesuwa się do przodu i cofa, jednakże wciąż podąża ku wyższemu potencjałowi.

Analogie

kulka	elektron
Ruch jednostajnie zmienny kulki w jednorodnym polu grawitacyjnym.	Ruch jednostajnie zmienny elektronu w jednorodnym polu elektrycznym.
Ruch jednostajny kulki w słoju z oleistą cieczą.	Ruch elektronu w przewodniku.

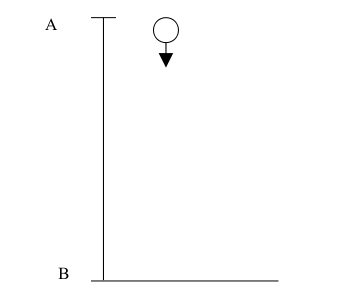
Ruch swobodnego elektronu w jednorodnym polu elektrycznym jest ruchem jednostajnie przyspieszonym, podobnie jak ruch kulki w jednorod­nym polu grawitacyjnym (rys. Figure 1).

Rozważmy tę sytuację dokładniej. W punk­cie A nadajemy kulce prędkość początkową [math]v_0[/math] pionowo w dół. Względem punktu B ma ona energię potencjalną grawitacji i energię kinetyczną. Gdy dotrze do punktu B ruchem jednostajnie przyspieszonym, będzie miała tylko energię kinetyczną równą sumie energii kinetycznej i potencjalnej, jaką miała w punkcie A. Jej prędkość będzie znacznie większa niż w punkcie A. A teraz nieco skomplikujmy tę sytuację. Tę samą kulkę umieścimy w tym samym punkcie A, ale w ośrodku stawiającym duży opór (np. w oleistej cieczy) Nadamy jej, jak poprzednio taką samą prędkość początkową [math]v_0[/math], ale na skutek równowagi sił będzie się ona poruszała ruchem jednostajnym. Kulka dotrze do punktu B i będzie miała tę samą prędkość co w punkcie A, a co za tym idzie, tę samą energię kinetyczną. Co się stało z energią potencjalną, jaką miała kulka w punkcie A? Na skutek tarcia zamieniła się na energię wewnętrzną kulki i ośrodka. Z ruchem elektronu w krysztale rzecz ma się bardzo podobnie. W jednorod­nym polu elektrycznym w próżni byłby to — jak wiesz — ruch jednostajnie przy­spieszony. W przewodniku można przyjąć, że średnia wartość prędkości elektronów w kierunku równoległym do osi przewodnika jest stała.

Praca i moc

Energia potencjalna pola elektrycznego zamienia się w energię wewnętrzną ośrodka, ponieważ elektron brnąc przez sieć krystaliczną metalu, zderza się z jonami i oddaje im część swojej energii, w wyniku czego rośnie amplituda drgań jonów, rośnie również energia wewnętrzna ośrodka. Ten wzrost energii wewnętrznej pociągnie za sobą wzrost temperatury.

W czasie [math]\Delta t[/math] płynął prąd o natężeniu I, a więc przez przewodnik przepłynął ładunek [math]\Delta q=I t\Delta[/math]. Przesuwając ładunek, siły pola elektrycznego wykonały pracę:

[math] W = \Delta q U = IU\Delta t [/math]

Tę wielkość nazywa się pracą prądu elektrycznego.

Jak pamiętasz pracę i energię wyraża się w dżulach i teraz warto podać związek jednostek wielkości mechanicznych z jednostkami wielkości elektrycznych

[math] \unit{l}{ J} =\unit{ 1}{V}\cdot \unit{1}{A} \cdot \unit{1}{s};\ \unit{1}{J}=\unit{ l}{ A^2} \cdot \unit{1}{\Omega} \cdot\unit{1}{ s}.[/math]

1 kilowatogodzina (kWh) jest to jednostka energii elektrycznej i pracy prądu. Odpowiada ona zużyciu energii elektrycznej przez urządzenie o mocy [math]\unit{1000}{W}[/math] pracujące w ciągu 1 godziny. [math]\unit{1}{kWh}= \unit{3,6 \cdot 10^6}{J}[/math].

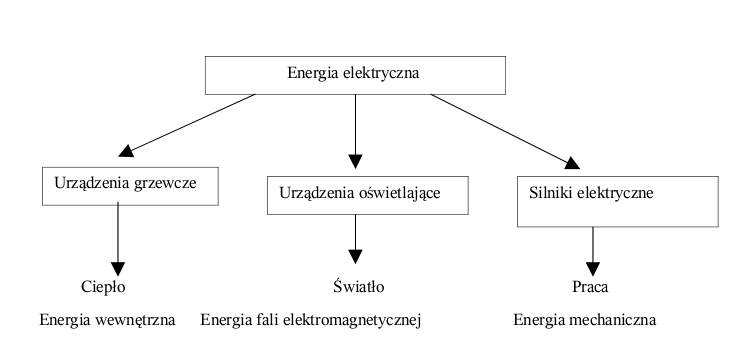
Wytwarzamy energię elektryczną głównie po to, żeby wykorzystywać ją w urządzeniach grzejnych ( kuchnie, grzejniki, suszarki do włosów), do oświetlania i do zasilania silników, które wykonują pracę mechaniczną. To są główne zastosowania prądu elektrycznego.

W urządzeniu grzewczym przepływający prąd rozgrzewa spiralę.

Dokładnie o wartość [math]W=IU \Delta t[/math] wzrosła energia wewnętrzna spirali i przekaże ona ten przyrost w formie ciepła otoczeniu

[math] W=Q[/math]

[math] Q = IU\Delta t[/math]

Ponieważ [math]U=IR[/math], więc

[math] Q = I^2 R\Delta t[/math]

Ciepło wydzielone przez przewodnik jest proporcjonalne do kwadratu natężenia 
przepływającego przezeń prądu oraz do czasu  jego przepływu.

Zależność tę po raz pierwszy odkrył James Prescott Joule. Od nazwiska tego uczonego pochodzi nazwa jednostki energii — dżul (J)

Jedną z charakterystycznych cech urządzeń grzewczych jest ich moc znamionowa.

Moc urządzenia elektrycznego

to szybkość, z jaką urządzenie to pobiera energię elektryczną, by ją przetworzyć na inny rodzaj energii:

[math]P = \frac{W}{\Delta t}[/math]

zatem

[math] P = UI = I^2 R = \frac{U^2}{R}[/math]

Jednostką mocy jest wat.

[math]\unit{1}{W} = \frac{\unit{1}{J}}{\unit{1}{s}}[/math]

[math] \unit{1}{W}=\unit{ l}{ A} \cdot\unit{1}{V};\ \unit{1}{W}=\unit{ l}{ A^2}\cdot\unit{1}{\Omega}[/math]

Każde urządzenie elektryczne charakteryzuje się również sprawnością.

Sprawność

urządzenia elektrycznego [math]\eta[/math] równa jest stosunkowi energii uzyskanej do pracy prądu elektrycznego, który zasila to urządzenie.

Sprawność realnie funkcjonujących urządzeń jest mniejsza od jedności, ponieważ część energii elektrycznej ulega rozproszeniu.