Fizyka III/Oscylator harmoniczny swobodny
Wstęp
Z wszelkiego radzaju drganiami mamy doczyniania w życiu codziennym. Na przykład codziennie korzystamy z prądu. Gdy pobieramy go z sieci miejskiej natężenie prądu zmienia się periodycznie z czasem. Jadąc na wykład dowolnym środkiem lokomocji mamy doczynienia z drganiami związanymi z amortyzatorami. Czasami mamy okazję dostrzec dziecko bujające się na huśtawce. Ruch huśtawki jest też przykładem drgań. Dochodzą do naszego ucha różne dźwięki. Są one źródłem drgań błony bębenkowej. Przykłady te możnaby powielać. Zwykle stykamy się z tzw. drganiami tłumionymi. Jednak na początek naszych rozważań skupmy uwage na drganiach swobodnych. Co zatem kryje się pod terminiem drgania swobodne?
Drganiami swobodnymi nazywamy periodyczną (okresową) w czasie zmianę stanu układu fizycznego, tzn. układ ten powraca do tych samych parametrów opisujących jego stan, co możemy zapisać następująco:
- [math]q_i(t) = q_i(t + T)[/math]
gdzie [math]q_i[/math] są parametrami opisującymi stan układu. Tymi parametrami mogą być różne wielkości fizycznę, np. położenie układu, prędkość, przyśpieszenie, natężenie prądu elektrycznego, ciśnienie, natężenie pola elektromagnetycznego, etc. Wielkość T nosi nazwę okresu. Odwrotność okresu nazywamy częstotliwością: [math]\nu = \frac{1}{T}[/math].
Przykładami ruchów okresowych układów fizycznych są: ruch masy zawieszonej na sprężynie, ruch wahadła matematycznego i fizycznego, drgania kamertonu i strun w instrumentach fizycznych, drgania atomów i cząsteczek, zmiany napięcia, ładunku i natężenia w obwodach elektrycznych LC, zmiany natężenia pola elektromagnetycznego.
Natomiast dowolny ruch chaotyczny, np. ruchy Browna, czy wszelkie postacie ruchu postępowego są przykładami ruchu nie będącego ruchem drgającym.
Jakie warunki musi spełniać układ fizyczny (dla ustalenia uwagi skoncentrujmy sie na układzie mechanicznym), żeby zachodziły w nim drgania swobodne? Warunki te są następujące:
- istnieje położenie równowagi trwałej (tzn. istnieje minimum energii potencjalnej, a więc istnieje siła zwrotna przywracająca stan równowagi),
- układ ma bezwładność (dla układów mechanicznych jest to masa),
- układ nie traci energii (nie ma żadnych sił oporu).
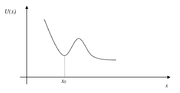
Na rysunku Figure 1 pokazano przykład energii potencjalnej posiadającej dla punktu [math]x=x_0[/math] minimum lokalne. Punkt [math]x_0[/math] jest punkt równowagi trwałej. Z reguły rozpatrujemy tzw. małe drgania, czyli taki ruch układu, że zmiana współrzędnej x jest niewielka w porównaniu z [math]x_0[/math]. W takim przypadku energię potencjalną, U(x) możemy rozwinąć na szereg wokół położenia równowagi:
- [math]U(x) = U(x_0)+(x-x_0)\frac{\mathrm dU}{\mathrm dx}\mid_{x_0}+\frac{1}{2}(x-x_0)^2\frac{\mathrm d^2U}{\mathrm dx^2}\mid_{x0}+\dots[/math]
Drugi składnik wzoru jest równy zeru, ponieważ rozwijamy funkcję [math]U(x)[/math] wokół jej minimum. Natomiast, ze względu na małe drgania pomijamy wyższe wyrazy w rozwinięciu. W takim przypadku energię potencjalną możemy zapisać:
- [math]U(x) = u(x_0)+\frac{1}{2}k(x-x_0)^2[/math]
We wzorze tym wprowadziliśmy oznaczenie noszące nazwę stałej sprężystości:
- [math]k=\frac{\mathrm d^2U}{\mathrm d x^2}\mid_{x_0}[/math]
W tym przybliżeniu zależność energii potencjalnej od odległości od położenia równowagi jest kwadratowa. W takim przypadku mówimy o oscylatorze harmonicznym. Biorąc pod uwagę, że siła jest równa:
- [math]F = -\frac{\mathrm d U}{\mathrm dx}[/math]
otrzymujemy wyrażenie na siłę:
- [math]F=-k(x-x_0)[/math].
Taką postać siły nazywamy siłą harmoniczną. Siła harmoniczna jest proporcjonalna do wychylenia z położenia równowagi, a jest zwrot jest skierowany do punktu równowagi.
Jeśli układ współrzędnych przyjmiemy tak, że [math]x_0 = 0[/math], to postać siły harmonicznej jest bardzo prosta: [math]F(x) = -kx[/math].
Równanie ruchu ma wówczas postać:
- [math]m\ddot{x} = -kx[/math]
gdzie m jest masą. Równanie to możemy przekształcić do formy:
- [math] \ddot{x} = -\frac k m x = -\omega_0^2 x[/math]
Powyższe równanie jest równaniem jednorodnym, liniowym drugiego rzędu o stałych współczynnikach. Rozwiązanie możemy łatwo odgadnąć. Poszukujemy bowiem funkcji [math]x=x(t)[/math], takiej, że dwukrotnie zróżniczkowana daje tę samą funkcję pomnożoną przez stałą ze znakiem ujemnym. Warunek taki spełniają dwie funkcje trygonometryczne: sinus i cosinus. Ogólne rozwiązanie będzie zatem kombinacją liniową obu funkcji:
- [math]x(t) = A \cos(\omega_0 t)+ B \sin(\omega_0 t)[/math]
Stałe A i B są stałymi całkowymi, które wyznaczamy z warunków początkowych, natomiast [math]\omega_0[/math] nosi nazwę częstości kołowej. Częstość ta wyraża się wzorem:
- [math]\omega_0 = \sqrt{\frac k m } = 2\pi \nu = \frac{2\pi} T[/math]
Przyjmijmy następujące warunki początkowe: położenie początkowe [math]x(t=0)= x_0[/math] oraz prędkość początkową [math]v(t=0)=V_0[/math]. Uwzględniając te warunki łatwo wyznaczamy stałe:
- [math]A = x_0\;[/math]
- [math]B = \frac{V_0}{\omega_0}[/math]
Stąd pełne rozwiązanie oscylatora harmonicznego jest postaci:
- [math]x(t) =x_0 \cos(\omega_0 t)+ \frac{V_0}{\omega_0} \sin(\omega_0 t) [/math]
Korzystając z tożsamości trygonometrycznych rozwiązanie to możemy zapisać w równoważny następujący sposób:
- [math] x= \sqrt{x_0^2+\left( \frac{V_0}{\omega_0}\right)^2}\cos(\omega_0 t +\delta)[/math]
gdzie [math]\delta[/math] nosi nazwę fazy, fazy początkowej lub przesunięciem fazowym i wyraża się wzorem:
- [math]\tg \delta =-\frac{V_0}{\omega_0 x_0}[/math]
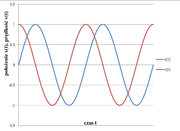
Na rysunku Figure 3 pokazano przykładowe zależności położenia i prędkości od czasu dla oscylatora harmonicznego.
Policzmy energię oscylatora harmonicznego. Przyjmijmy rozwiązanie postaci:
- [math]x(t) = A_0 \cos(\omega_0 t +\delta)[/math]
Prędkość wówczas wynosi:
- [math]v(t) = -\omega_0 A_0 (\omega_0 t +\delta)\sin [/math]
Stąd łatwo możemy policzyć energię kinetyczną:
- [math]E_k = \frac{m v^2}{2} = \frac{1}{2}m \omega_0^2A_0^2\sin^2(\omega_0 t +\delta) [/math]
i energię potencjalną:
- [math]E_p = \frac{kx^2}{2} = \frac{1}{2} k A_0^2\cos^2(\omega_0 t +\delta) [/math]
Energia całkowita jest stała i wynosi:
- [math]E_k + E_p = \frac{1}{2}m \omega_0^2A_0^2\sin^2(\omega_0 t +\delta) + \frac{1}{2} k A_0^2\cos^2(\omega_0 t +\delta) = \frac{1}{2} k A_0^2 \left( \sin^2(\omega_0 t +\delta) +\cos^2(\omega_0 t +\delta) \right) = \frac{1}{2} k A_0^2 [/math]
Na rysunku Figure 3 pokazano dla rozważanego oscylatora zależność energii potencjalnej i kinetycznej od czasu.
Warto zwrócić uwagę, że ruch harmoniczny można powiązać z ruchem po okręgu — taki wniosek wyciągnął Galileusz w roku 1610 obserwując ruch księżyców Jowisza. Ruch harmoniczny jest bowiem ruchem rzutu punktu poruszającego się po okręgu na średnicę okręgu po którym ten ruch się odbywa.
Teraz kilka przykładów układów fizycznych wykonujących ruch harmoniczny.
Przykład 1. Wahadło matematyczne.
Wahadło matematyczne składa się z punktu materialnego o masie m zawieszonego na nieważkiej nici o długości L. Jeśli wahadło wychylimy z położenia równowagi o kąt [math]\theta[/math] (patrz rysunek Figure 4), to spełnione jest równanie:
- [math]I\overrightarrow{\varepsilon} = \overrightarrow{M} = \overrightarrow{r}\times\overrightarrow{F}[/math]
gdzie I jest momentem bezwładności, [math]\overrightarrow{\varepsilon}[/math] przyśpieszeniem kątowym, M momentem siły, r — ramieniem, a F — siłą. Zgodnie z rysunkiem Figure 4 równanie to możemy przekształcić do postaci:
- [math]I\frac{\mathrm d^2\theta}{\mathrm d t^2} = -mgL\sin\theta[/math]
- [math]mL^2\frac{\mathrm d^2\theta}{\mathrm d t^2} = -mgL\sin\theta[/math]
- [math]\frac{\mathrm d^2\theta}{\mathrm d t^2} = -\frac{g}{L}\sin\theta[/math]
Jeśli dalej założymy, że wychylenia z położenia równowagi (kąt [math]\theta[/math]) są małe to wówczas [math]\sin\theta \approx \theta[/math] i otrzymujemy na kąt wychylenia równanie oscylatora harmonicznego:
- [math]\frac{\mathrm d^2\theta}{\mathrm d t^2} = -\frac{g}{L}\theta[/math]
- [math]\omega_0 = \sqrt{\frac{g}{L}}[/math]
Pozostaje pytanie co to znaczy małe wychylenie. Na rysunku Figure 5 pokazano funkcję liniową (linia różowa) oraz funkcję sin(x) (linia niebieska) w funkcji kąta, natomiast w poniżej tabeli zebrano wartości obu tych funkcji.
| stopnie | radiany | sin(x) |
|---|---|---|
| 1 | 0,017452 | 0,017453 |
| 2 | 0,034899 | 0,034907 |
| 3 | 0,052336 | 0,05236 |
| 4 | 0,069756 | 0,069813 |
| 5 | 0,087156 | 0,087266 |
| 6 | 0,104528 | 0,10472 |
| 7 | 0,121869 | 0,122173 |
| 8 | 0,139173 | 0,139626 |
| 9 | 0,156434 | 0,15708 |
| 10 | 0,173648 | 0,174533 |
| 11 | 0,190809 | 0,191986 |
| 12 | 0,207912 | 0,209439 |
| 13 | 0,224951 | 0,226893 |
| 14 | 0,241922 | 0,244346 |
| 15 | 0,258819 | 0,261799 |
| 16 | 0,275637 | 0,279252 |
| 17 | 0,292371 | 0,296706 |
| 18 | 0,309017 | 0,314159 |
| 19 | 0,325568 | 0,331612 |
| 20 | 0,34202 | 0,349066 |
Z rysunku oraz z powyższej tabeli wynika, że dla wychylenia o 10 stopni względny błąd przybliżenia funkcji sinus jej argumentem jest na poziomie 0,5%.
Przykład 2. Wahadło fizyczne
Na rysunku Figure 7 schematycznie pokazano wahadło fizyczne. W tym przypadku siła ciężkości wahadła jest przyłożona w jego środku ciężkości, tj. w punkcie odległym o h od osi obrotu. Równanie ruchu wahadła fizycznego jest bardzo podobne do równania ruchu wahadła matematycznego, tj.:
- [math]I\frac{\mathrm d \theta}{\mathrm d^2 t} = -m g h \sin\theta[/math]
Zakładamy, że amplituda drgań jest mała, tzn. przyjmujemy: [math]\sin(\theta)=\theta[/math] i wówczas otrzymujemy równanie oscylatora harmonicznego:
- [math]I\frac{\mathrm d \theta}{\mathrm d^2 t}= -m g h\theta[/math]
Stąd częstość kołowa i okres drgań wahadła wynoszą odpowiednio:
- [math]\omega_0 = \sqrt{\frac{mg h}{I}}[/math]
- [math]T = 2\pi\sqrt{\frac{I}{mg h}} [/math]
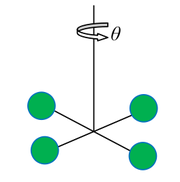
Przykład 3. Wahadło torsyjne.
Dla wahadła torsyjnego (Figure 8) równanie ruchu ma postać:
- [math]I\frac{\mathrm d^2\theta}{\mathrm dt^2}=-\kappa \theta[/math]
Gdzie [math]\kappa[/math] nosi nazwę momentu kierującego. Powyższe równanie jest równaniem oscylatora harmonicznego z częstością kołową:
- [math]\omega_0=\sqrt{\frac{\kappa}{I}}[/math]
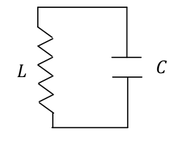
Przykład 4. Drgania w obwodzie LC.
Na rysunku Figure 9 przedstawiono obwód składający się z cewki o indukcyjności L i kondensatora o pojemności C (tzw. obwód LC).
Dla takiego obwodu spełnione jest równanie:
- [math]\mathrm{SEM} - L \frac{\mathrm d I}{\mathrm dt}= \frac{Q}{C}[/math]
gdzie: I jest natężeniem prądu płynącego w obwodzie, Q ładunkiem na kondensatorze, a SEM siłą elektromotoryczną. Powyższy obwód jest obwodem idealnym bo pomijamy wszelkie opory elektryczne. Ponadto: SEM=0, i w takim przypadku równanie na ładunek jest równaniem oscylatora harmonicznego:
- [math]L\frac{\mathrm d^2 Q}{\mathrm dt^2} +\frac 1 C Q = 0[/math]
którego rozwiązaniem jest [math]Q=Q_0\cos(\omega_0 t +\delta)[/math], gdzie [math]\omega_0=\frac 1 \sqrt{LC}[/math].
Energia całkowita układu jest stała i wynosi [math]E=E_L+E_K =\frac 1 2 LI^2 +\frac 1 2 \frac{Q^2} C =\frac{Q_0^2}{2C}[/math]:
Wahadło matematyczne (proste).
Wróćmy do rozważań dotyczących wahadła matematycznego i zastanówmy się jaki jest okres drgań wahadła, jeśli amplituda drgań nie jest mała, tzn. gdy nie jest spełniony warunek [math]\sin(\theta)=\theta[/math]. Z zasady zachowania energii wynika:
- [math]E_k =\frac 1 2 mv^2=\frac 1 2 m \dot{\theta}^2L^2[/math]
- [math]E_p = mgh = mgL(1-\cos\theta)[/math]
Stąd otrzymujemy równanie:
- [math]\dot{\theta}^2=2\omega_0^2\cos\theta+\Gamma[/math]
- [math]\omega_0^2=\frac g L[/math]
gdzie:
- [math]\Gamma=\frac{2E}{mL^2}-\frac{2g}L[/math]
Załóżmy, że maksymalne wychylenie wahadła z położenia równowagi wynosi [math]\theta_0[/math]. Dla tego punktu (tzw. punktu zwrotnego) zachodzi: [math]\dot\theta=0\Longrightarrow \cos\theta_0=-\frac{\Gamma}{2\omega_0^2}[/math]. Stąd otrzymujemy wyrażenie na okres drgań (okres ten jest równy 4 razy czas potrzebny na pokonanie dystansu od położenia równowagi do maksymalnego wychylenia):
- [math]T = 4\int_0^{\theta_0}\frac{\mathrm d\theta}{\sqrt{2\omega_0^2\cos\theta +\Gamma}}=\frac{2}{\sqrt{2\omega_0^2}}\int_0^{\theta_0}\frac{\mathrm d\theta}{\sqrt{\cos\theta-\cos\theta_0}}[/math]
Wprowadzając podstawienie [math]\sin\phi = \frac{\sin\frac\theta 2}{\sin\frac{\theta_0} 2}[/math] otrzymujemy następującą całkę (zwaną całką eliptyczną zupełną pierwszego rodzaju):
- [math]T =\frac{4}{\omega_0}\int_0^{\frac{\pi}{2}}\frac{\mathrm d\phi}{\sqrt{1-\sin^2\frac{\theta_0}{2}\sin^2\phi}}[/math]
Korzystając z tablic całek ostatecznie wyrażenie na okres drgań ma postać:
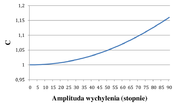
- [math]T=2\pi\sqrt\frac L g\left(1+\frac 1 4 \sin^2\frac{\theta_0}2+ \frac 9 64 \sin^4\frac{\theta_0}2+\ldots\right)=2\pi\sqrt\frac L g C[/math]
Widać, ze w tym przypadku okres drgań zależy od amplitudy drgań (rysunek Figure 10).
Rezonans parametryczny wahadła matematycznego.
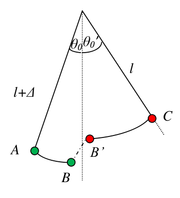
Pewnie wielu z nas miało okazję huśtać się na huśtawce. Na podstawie tego „doświadczenia” wiemy, że istnieje możliwość rozbujania się poprzez wyciąganie i podciąganie nóg. Takie „zjawisko” nazywamy rezonansem parametrycznym. Przeanalizujmy rezonans parametryczny na przykładzie wahadła matematycznego pokazanego na rysunku Figure 11.
Ruch wahadła odbywa się najpierw od punktu zwrotnego A (wychylenie o kąt [math]\theta_0[/math]) do punktu B. Podczas tego ruchu długość wahadła wynosi [math]l+\Delta[/math]. W punkcie równowagi zmienia się długość wahadła z [math]l+\Delta[/math] na l (przejście z punktu B do punktu B’). Następnie wahadło porusza się do punktu zwrotnego C (wychylenie o kąt [math]\theta_0'[/math]). Energia kinetyczna wahadła w punkcie B jest równa zmianie energii potencjalnej z punktu A do punktu B:
- [math]\Delta E= E_A-E_B=mg(l+\Delta)(1-\cos\theta_0)=E_{\mathrm{kin}B}=\frac m2 \left(\frac{\mathrm d\theta}{\mathrm dt}\right)^2(l+\Delta)^2[/math]
Stąd kwadrat prędkości kątowej w punkcie B: .
- [math]\left(\frac{\mathrm d\theta}{\mathrm dt}\right)^2\mid_B=\frac{2g(1-\cos\theta_0)}{l+\Delta}[/math]
W analogiczny sposób z zasady zachowania energii znajdujemy kwadrat prędkości kątowej w punkcie B’: [math]\left(\frac{\mathrm d\theta}{\mathrm dt}\right)^2\mid_{B'}=\frac{2g(1-\cos\theta_{0'})}{l+\Delta}[/math]. Dalej korzystamy z zasady zachowania momentu pędu gdy wahadło przechodzi przez punkt równowagi [math]I_B\omega_B=I_{B'}\omega_{B'}[/math]: gdzie I jest momentem bezwładności, a [math]\omega[/math] prędkością kątową. Zasadę tę zapisujemy w postaci:
- [math]m(l+\Delta)^2\left(\frac{\mathrm d\theta}{\mathrm dt}\right)\mid_B=ml^2\left(\frac{\mathrm d\theta}{\mathrm dt}\right)\mid_{B'}[/math]
Do tego równania wstawiamy wyliczone wyżej prędkości kątowe i otrzymujemy równość:
- [math](l+\Delta)^3(1-\cos\theta_0)=l^3(1-\cos\theta_{0'})[/math]
Równość ta jest spełniona gdy [math]\cos\theta_0\gt \cos\theta_{0'}[/math], a stąd korzystając z własności funkcji cosinus otrzymujemy: [math]\theta_{'0}\gt \theta_0[/math]. A więc skracając długość wahadła w momencie przechodzenia przez punkt równowagi zwiększyliśmy kąt wychylenia w punkcie zwrotnym. W ten sposób możemy rozbujać huśtawkę zwiększając amplitudę drgań.
Oscylator anharmoniczny
Na początku tego rozdziału zajmowaliśmy się drganiami harmonicznymi, a więc ruchem układu mechanicznego, którego energia potencjalna jest funkcją paraboliczną (kwadratową) wychylenia z położenia równowagi. Zastanówmy się jak zmienia się ruch układu jeśli w rozwinięciu energii potencjalnej wokół położenia równowagi uwzględnimy wyższe wyrazy, a więc gdy zależność energii potencjalnej od położenia jest na przykład postaci:
- [math]U(x)=\frac 1 2 kx^2-\frac 1 3 sk x^3[/math]
Rozpatrujemy przypadek taki, że poprawka [math]-\frac 1 3 sk x^3[/math] jest bardzo mała, tzn. parametr s pomnożony przez amplitudę drgań jest dużo mniejszy od jedynki — [math]sA\ll 1[/math]. Siła wyraża się w takim przypadku wzorem: [math]F = -kx+skx^2 [/math], a stąd otrzymujemy równania:
- [math]\ddot{x}+\omega_0^2x-\omega_0^2 s x^2=0[/math]
Ponieważ poprawka do energii potencjalnej jest mała, to poszukujemy rozwiązania postaci:
- [math]x=A(\cos(\omega t)+ q\cos(2\omega t))+x_1[/math]
Zakładamy więc, że rozwiązanie składa się z rozwiązania oscylatora harmonicznego oraz poprawek: wyrazu zawierającego wielokrotność częstości kołowej podstawowej oraz wyraz stały. Oba te wyrazy powinny być małe, tzn. [math]q\ll1[/math], a [math]x_1\ll A[/math]. Policzmy prędkość i przyśpieszenie, a następnie podstawmy do równania ruchu:
- [math]\dot{x} = -A\omega(\sin(\omega t)+2q\sin(2\omega t))[/math]
- [math]\ddot{x} = -A\omega^2(\cos(\omega t)+4q\cos(2\omega t))[/math]
Wykorzystując tożsamość trygonometryczną:
- [math]\cos^2\alpha =\frac 1 2 + \frac 1 2 \cos(2\alpha)[/math]
otrzymujemy:
- [math]-A\omega^2(\cos\omega t +4q\cos2\omega t) +A\omega_0^2(\cos\omega t +q\cos2\omega t)+\omega_0^2x_1-s\omega_0^2A^2\cos^2\omega t +\ldots = 0[/math]
Z porównania współczynników przy [math]\cos\omega t[/math] wynika:
- [math]\cos(\omega t)A(\omega_0^2-\omega^2)=0\Longrightarrow \omega_0=\omega[/math]
Natomiast z porównania współczynników przy [math]\cos2\omega t[/math]:
- [math]\cos(2\omega t)A(\omega_0^2q-4\omega^2q-\frac 1 2 s\omega^2_0 A)=0[/math]
otrzymujemy:
- [math]q=-\frac 1 6 sA[/math].
Przyrównując wyraz stały do zera znajdujemy: [math]x_1=\frac 1 2 sA^2[/math]. „Pełne” rozwiązanie równania w ramach przyjętego przybliżenia jest następujące:
- [math]x=A\left(\cos\omega_0t -\frac 1 6 sA \cos2\omega_0t\right)+ \frac 1 2 sA^2[/math]
Widzimy więc, ze poprawka do potencjału harmonicznego powoduje, że w rozwiązaniu pojawiają się drgania z częstością kołową będącą wielokrotnością częstości podstawowej (tzw. wyższe harmoniczne) oraz wyraz stały (następuje przesuniecie położenia równowagi).
Warto zwrócić uwagę, że w cząsteczkach (np. H2, CO2, etc.) jądra wykonują drgania, które w przybliżeniu są drganiami harmonicznymi. Jednakże w przybliżeniu harmonicznym nie można zrozumieć np. rozszerzalności (wydłużania się) długości wiązania (odległości miedzy jadrami cząsteczki) ze wzrostem temperatury. To zjawisko można zrozumieć w przybliżeniu rozpatrywanym wyżej oscylatora anharmonicznego. W rozwiązaniu pojawia się bowiem wyraz stały proporcjonalny do kwadratu amplitudy drgań. Średnie położenie oscylatora harmonicznego (a więc np. średnia długość wiązania w cząsteczce) zmienia się liniowo z temperaturą, co jest znanym faktem eksperymentalnym:
- [math]\langle x\rangle=\frac 1 2 sA^2\propto T[/math]
Bardzo wiele zjawisk fizycznych z dobrym przybliżeniem można opisać za pomocą oscylatora harmonicznego. Są jednak i takie zjawiska, jak opisane wyżej, że opis wymaga wyjścia poza to przybliżenie.