Fizyka III/Drgania tłumione
Wstęp
Większość drgań w rzeczywistych układach fizycznych ma charakter tłumiony. Wynika to z faktu, że prawie zawsze występują opory, np. opór powietrza podczas drgań sprężyny lub ruchu wahadła albo opór elektryczny w obwodach elektrycznych. W przypadku oporu powietrza, siła oporu działająca na kulkę o promieniu R wyraża się wzorem Stokesa:
- [math]\vec F = - 6\pi \eta r \vec v[/math]
gdzie v jest prędkością kulki a [math]\eta[/math] współczynnikiem lepkości. Dla powietrza [math]\eta= \unit{1,8\times 10^5}{\frac{kg}{ms}}[/math]. W przypadku obwodów elektrycznych spadek napięcia spowodowany oporem elektrycznym R wynosi:
- [math]U=-IR = -R \ddot Q[/math]
W obu przypadkach pojawia się siła oporu proporcjonalna do pochodnej po czasie zmiennej opisującej ruch. Nasze rozważania dotyczące drgań tłumionych ograniczymy do rozważań układów w których występuje siła harmoniczna oraz siła oporu postaci [math]F_{op} = -b \frac{\mathrm d x}{\mathrm d t} = -b v[/math]. W takim przypadku równanie opisujące ruch układu jest następujące:
- [math]m\ddot x = -kx -b\dot x[/math]
Po prostych przekształceniach i wprowadzeniu oznaczeń: [math]2\beta = \frac b m,\ \omega_0^2 = \frac k m[/math], otrzymujemy równanie różniczkowe:
- [math]\ddot x +2\beta \dot x +\omega_0^2 x=0 [/math]
Jest to równanie różniczkowe jednorodne drugiego rzędu o stałych współczynnikach. Tego typu równania rozwiązujemy poszukując rozwiązania postaci: [math]x = Ae^\lambda[/math]. Po podstawieniu do równania postulowanego rozwiązania otrzymujemy równanie kwadratowe na parametr [math]\lambda[/math]:
- [math]\lambda^2+2\beta\lambda+\omega_0^2=0[/math]
W zależności od wielkości parametru tłumienia [math]\beta[/math] względem częstości kołowej ruchu swobodnego [math]\omega_0[/math] pierwiastki równania kwadratowego przyjmują różne wartości.
Przypadek 1 [math](\beta \lt \omega_0)[/math]
W tym przypadku otrzymujemy dwa pierwiastki o wartościach zespolonych: [math]\lambda_{1,2}=-\beta\pm i\omega[/math], gdzie [math]\omega=\sqrt{\omega_0^2-\beta^2}[/math]. Rozwiązanie równania ruchu jest następujące:
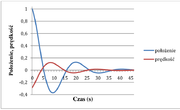
Stałe [math]A_0[/math] i [math]\delta[/math] wyznaczamy z warunków początkowych. Ten przypadek nazywamy oscylatorem słabo tłumionym. Rozwiązanie ma postać czynnika oscylacyjnego [math]\cos(\omega t +\delta)[/math] oraz amplitudy [math]A(t)=A_0e^{-\beta t}[/math] która maleje z czasem. Postać zależności [math]x(t)[/math] pokazano na rysunku Figure 1. Zwróćmy uwagę, że obecność siły oporu powoduje zmniejszanie się z czasem amplitudy drgań oraz zmniejszenie się częstości drgań (zwiększenie okresu). Im większa wartość parametru oporu tym szybciej maleje amplituda drgań i tym większy okres drgań: [math]T=\frac{2\pi}{\sqrt{\omega_0^2-\beta^2}}[/math]. Dla oscylatora harmonicznego słabo tłumionego wprowadzamy następujące wielkości charakteryzujące jego ruch:
- Czas relaksacji [math]\tau[/math] zdefiniowany: [math]\frac{A(t)}{A(t+\tau)}=e[/math], stąd: [math]\tau=\nicefrac 1 \beta[/math].
- Logarytmiczny dekrement tłumienia: [math]\Lambda = \ln \frac{A(t)}{A(t+\tau)}=\beta T = \frac b {2m}T[/math].
- Dobroć układu drgającego: [math]Q=2\pi\frac{E}{\Delta E(t,t+T)} = \frac\pi\Lambda=\frac \pi{\beta T} = \frac{\pi\tau}T [/math].
Dla oscylatora harmonicznego swobodnego energia układu jest stała. W przypadku oscylatora tłumionego energia układu musi maleć, ze względu na występowanie siły oporu. Policzmy zatem średnią energię oscylatora tłumionego. Przyjmijmy, że położenie opisane jest funkcją: . Po prostych przekształceniach otrzymujemy prędkość: , gdzie przesunięcie fazowe prędkości względem położenia wynosi: . Na rysunku Figure 1 pokazano dla tego przypadku przykład zależności położenia i prędkości od czasu.
Teraz przystępujemy do policzenia średniej energii układu:
- [math]\langle E_p\rangle=\langle\frac 1 2 k A^2e^{-2\beta t }\cos^2 \omega t\rangle\approx \frac 1 4 k A^2 e^{-2\beta t}[/math]
- [math]\langle E_k\rangle=\langle \frac 1 2 m A^2\omega_0^2e^{-2\beta t }\cos^2( \omega t-\Phi)\rangle\approx \frac 1 4 k A^2 e^{-2\beta t}[/math]
Przy uśrednianiu założyliśmy, że tłumienie jest bardzo słabe, tzn. amplituda drgań w czasie jednego okresu „prawie” się nie zmienia, co matematycznie oznacza wyłączenie czynnika [math]e^{-2\beta t}[/math] przed całkę. Stąd otrzymujemy średnią energię całkowitą układu:[math]\langle E\rangle = \frac 1 2 kA^2 e^{-2\beta t}[/math] oraz średnią moc traconą przez układ: [math]\langle P\rangle = \frac{\mathrm \langle E\rangle}{\mathrm dt} = -k\beta A^2e^{-2\beta t}[/math].
Moc traconą przez układ możemy policzyć również w sposób następujący:
- [math]\langle P\rangle = \langle F_{op} v\rangle =\langle bv\cdot v\rangle = \langle -2\beta m A^2 e^{-2\beta t}\omega_0^2\cos^2(\omega t -\Phi)\rangle\approx -\beta k A^2 e^{-2\beta t}[/math]
Wyprowadziwszy wzory na energie i moc możemy łatwo policzyć dobroć układu:
- [math]Q = 2\pi \frac{\langle E\rangle}{\langle P\rangle T}=2\pi \frac{\frac 1 2 k A^2 e^{-2\beta t}}{\beta kA^2e^{-2\beta t} T}=\frac{2\pi}{2\beta T}= \frac{\omega}{2\beta}[/math]
Kilka typowych wartości dobroci Q:
- Ziemia dla fal sejsmicznych 250-1400
- Struna fortepianu lub skrzypiec 103
- Rezonator mikrofal z wnęką miedzianą 104
- Atom wzbudzony 107
- Jądro wzbudzone 1012
Przypadek 2 ([math]\beta=\omega_0[/math])
Ten przypadek nosi nazwę tłumienia krytycznego, gdyż dla tego przypadku układ wraca najszybciej do stanu równowagi.
Rozwiązanie ma postać:
- [math]x= (A+Bt)e^{-\beta t}[/math]
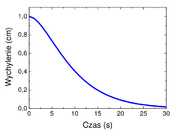
Stałe A i B wyznaczamy z warunków początkowych. Np. jeśli warunki początkowe są następujące: [math]x(t=0)=x_0,\ v(t=0)=0[/math], to rozwiązanie ma postać (rysunek Figure 2):
- [math]x=x_0(1+\beta t)e^{-\beta t}[/math]
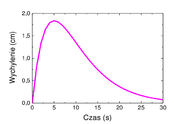
Natomiast jeśli układ w chwili początkowej był w położeniu równowagi [math](x(t=0)=0)[/math] i nadano mu pewną prędkość to rozwiązanie jest następujące (rysunek Figure 3):
- [math]x=V_0te^{-\beta t}[/math]
Przypadek 3 [math](\beta\gt \omega_0)[/math]
Ten przypadek nosi nazwę tłumienia silnego. Rozwiązanie jest sumą dwóch funkcji wykładniczych:
- [math]x(t)=A_1e^{\lambda_1t}+A_2e^{\lambda_2t}[/math]
gdzie [math]\lambda_{1,2} = -\beta \pm\sqrt{\beta^2-\omega_0^2}[/math].
Obwód RLC
Identyczne równania (i przypadki) otrzymujemy dla obwodów elektrycznych składających się z połączonych szeregowo: opornika o oporze R, kondensatora o pojemności C i cewki o indukcyjności L:
- [math]\frac{\mathrm d^2Q}{\mathrm dt^2} + \frac RL +\frac 1{LC} Q = 0[/math]
Dla przypadku [math]\frac1{LC}\gt \frac{R^2}{4L^2}[/math] (oscylator słabo tłumiony) rozwiązanie jest następujące:
- [math]Q=Q_0e^{-\beta t}\cos(\omega t+\delta)\;[/math]
gdzie:
- [math]\omega = \sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}[/math].