Fizyka III/Fale na powierzchni wody

Pewnie każdy z nas nie raz miał okazję przyglądać się falom na powierzchni wody. Jak wspominaliśmy na początku rozważań o falach, fale na powierzchni wody nie są falami ani podłużnymi ani poprzecznymi. Cząsteczki wody mogą wykonywać dość skomplikowany ruch. Funkcja falowa opisująca te fale nie spełnia klasycznego równania falowego. Prędkość rozchodzenia się fal na wodzie zależy od długości fal. To są zasadnicze różnice w porównaniu do fal na strunie czy fal dźwiękowych. W niniejszych rozważaniach ograniczymy się do najprostszego opisu pomijając niektóre własności wody, np. nie będziemy uwzględniać lepkości, która jest przyczyną powstawania wirów. Zainteresowanych bardziej zaawansowanym opisem fal na wodzie (w cieczach) odsyłamy do literatury specjalistycznej.

W naszym najprostszym opisie przyjmijmy następujące założenia (patrz rysunek Figure 1):

1. Woda znajduje się w długim kanale o prostokątnym przekroju i głębokości h.
2. Ruch fali wzdłuż współrzędnych z i y jest niezależny od współrzędnej x.
3. Woda jest nieściśliwa (w fali 1 m wzrost gęstości o około 0.05%).

Zbiornik wody o głębokości h.

Przyjmujemy, że wychylenie cząsteczek z położenia równowagi opisane jest funkcjami:

[math]\Psi_y(y,z,t)=A_y(y)\cos(\omega t -kz)\;[/math]

[math]\Psi_z(y,z,t)=A_z(y)\cos(\omega t -kz)\;[/math]

Zakładamy również następujące warunki brzegowe:

1. Na powierzchni wody [math](y=0):\ \Psi_y(0,z,t) =A\cos(\omega t-kz) [/math].
2. Na dnie nie ma ruchu pionowego cząsteczek wody: [math]A_y(-h)=0\;[/math]

Przyjęte założenia prowadzą do następujących wyrażeń:

[math]A_y(y)=\frac{A\sinh[k(h+y)]}{\sinh kh}[/math]

[math]A_z(y)=\frac{A\cosh[k(h+y)]}{\sinh kh}[/math]

W rozpatrywanym prostym modelu cząsteczki wody poruszają się po elipsach:

[math]\left(\frac{\Psi_y}{A_y}\right)^2+\left(\frac{\Psi_z}{A_z}\right)^2=1[/math].

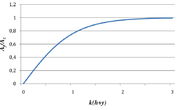
Na rysunku Figure 2. pokazano jak zmienia się stosunek [math]\nicefrac{A_y}{A_z}[/math] ze zmianą głębokości.

Stosunek amplitud [math]\nicefrac{A_y}{A_z}[/math] w funkcji głębokości.

Widzimy, ze im głębiej, tym oś pozioma dłuższa, czyli elipsa bardziej płaska, aż do prostej na dnie. Pozioma oś też ulega skróceniu, ale wolniej niż pionowa. Ruch cząsteczek wody jest zgodny z ruchem wskazówek zegara dla fali biegnącej w prawo. Cząsteczka wody na grzbiecie fali porusza się tylko do przodu, w dolinie — tylko do tyłu (patrz rysunek Figure 3).

Ruch cząsteczek wody.

Gdy rozpatrujemy ruch cząsteczek na głębokiej wodzie, tzn. gdy spełnione są warunki: [math]|y|\ll h,\ kh\gg 1\Rightarrow \lambda\ll h[/math], to funkcje falowe mają postać:

[math]\Psi_y(y,z,t)\approx Ae^{ky}\cos(\omega t -kz)[/math]

[math]\Psi_z(y,z,t)\approx Ae^{ky}\sin(\omega t -kz)[/math]

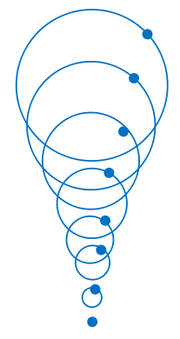
Na głębokiej wodzie orbity po których poruszają się cząsteczki wody są okręgami, których promień maleje wykładniczo z głębokością i na głębokości większej niż [math]\frac 1{|k|}[/math] ruch praktycznie zanika (patrz rysunek Figure 4). Z tego powodu np. pływaki platform wiertniczych są zanurzone głęboko, a więc tam gdzie ruch falowy jest niewielki.

Ruch cząsteczek wody na głębokiej wodzie.

Z kolei na płytkiej wodzie, a wiec gdy spełniony jest warunek: funkcje falowe przyjmują postać:

[math]\Psi_y(y,z,t)\approx A\left(1+\frac yh\right)\cos(\omega t -kz)[/math]

[math]\Psi_z(y,z,t)\approx A\left(\frac 1{kh}\right)\cos(\omega t -kz)[/math]

W tym przypadku amplituda pozioma praktycznie nie zależy od głębokości i jest bardzo duża, fala jest głównie podłużna. Natomiast amplituda pionowa maleje prawie liniowo z głębokością (do zera na dnie). Woda przelewa się „tam i z powrotem”.

Dla fal na strunie oraz fal dźwiękowych związek łączący częstość kołową i wartość wektora falowego jest bardzo prosty: [math]\omega=vk\;[/math], gdzie prędkość fali jest stała [math](v=const)\;[/math] i nie zależy od długości fali. Dla fal na wodzie związek ten jest bardziej skomplikowany. Wyprowadza się go korzystając z prawa Bernouliego. Całkowita energia na jednostkę masy W wynosi:

[math]W=\frac p\rho +\frac 12 v^2 +V[/math],

gdzie: p — ciśnienie, [math]\rho[/math] — gęstość, v — prędkość płynu, V — energia potencjalna na jednostkę masy. Energia [math]V=g\Psi\;[/math] (g — przyśpieszenie ziemskie, [math]\Psi\;[/math] — funkcja falowa), natomiast ciśnienie: [math]p=p_0-\sigma\frac{\partial^2\Psi}{\partial z^2}[/math], gdzie: [math]\sigma[/math] — napięcie powierzchniowe ([math]\sigma = \unit{0,073}{\frac{N}{m}}[/math] dla granicy woda/powietrze w 20°C), a [math]p_0[/math] — ciśnienie atmosferyczne.

Związek dyspersyjny dla fal na wodzie jest następujący: [math]\omega^2=\left(\frac gk+\frac{\sigma k^2}{h\rho}\right)[/math]. W oparciu o ten związek często podaje się przybliżony wzór na prędkość fazową fal na wodzie:

[math]v_f=\sqrt{\frac{\lambda g}{2\pi}+\frac{2\pi \sigma}{\lambda \rho}}[/math].

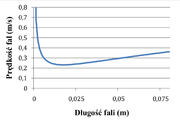
W zależności dyspersyjnej są dwa składniki: grawitacyjny (opadanie wody) i kapilarny („prostowanie” powierzchni wywołane siłą napięcia powierzchniowego). Powyższa zależność jest pokazana na rysunku Figure 5.

Prędkość fazowa fal na wodzie.

Zwróćmy uwagę, że dla fal krótkich prędkość fali maleje wraz z długością fali. Ten zakres fal nazywamy zakresem dyspersji anomalnej. Dla fal krótkich decydującym czynnikiem są siły napięcia powierzchniowego, natomiast dla fal długich decydujące znaczenie ma czynnik grawitacyjny. Równość obu wkładów (grawitacyjnego i kapilarnego) daje graniczną długość fali: dla wody [math]\lambda_0=2\pi\sqrt{\frac\sigma{g\rho}}[/math] w 20°C. Dla fal dużo krótszych (powierzchnia mocniej pozakrzywiana) decyduje napięcie powierzchniowe, wkład grawitacyjny można zaniedbać. W takim przypadku mówimy o falach kapilarnych („zmarszczkach na wodzie”). Na płytkiej wodzie dla fal kapilarnych związek dyspersyjny przyjmuje postać: [math]\omega = \sqrt{\frac{\sigma k^3}\rho}[/math], a prędkość fali: [math]v_f=\frac{\omega}{k}\approx \sqrt{\frac{2\pi\sigma}{\rho\lambda}}[/math]. Na przykład dla [math]\lambda=\unit 1{mm}[/math] prędkość fali wynosi: [math]v_f=\unit{0,68}{\frac ms}[/math]. Dla fal kapilarnych najkrótsze fale poruszają się najszybciej.

Z kolei na głębokiej wodzie związek dyspersyjny jest następujący: [math]\omega =\sqrt{\frac{\sigma}{h\rho}}[/math], co oznacza, ze prędkość fal kapilarnych jest stała: [math]v_s=\sqrt{\frac\sigma{h\rho}}[/math].

Dla fal spełniających warunek [math]\lambda \gg \unit{17}{mm}[/math] można zaniedbać wpływ napięcia powierzchniowego i wówczas mówimy o falach grawitacyjnych. W przypadku tego rodzaju fal na głębokiej wodzie związek dyspersyjny jest następujący: [math]\omega =\sqrt{gk}[/math], a stąd prędkość fazowa fali [math]v_f\cong \sqrt \frac gk=\sqrt{\frac{g\lambda}{2\pi}}[/math]. Widzimy, że dłuższe fale grawitacyjne poruszają się szybciej niż krótsze, a więc jeśli fale są wywołane daleko to pierwsze dotrą do brzegu fale najdłuższe. Dla płytkiej wody: [math]\omega =\sqrt{gh}k[/math] i w takim przypadku oczywiście prędkość fazowa jest stała [math]v_f=\sqrt{gh}[/math] i np. dla zbiornika o głębokości [math]\unit{6100}{m}[/math] wynosi: [math]v_f=\unit{245}{\frac ms}=\unit{881}{\frac{km}{h}}[/math].

Czasami gdy źródłem fal są trzęsienia Ziemi na dnie oceanu lub meteoryty, powstają fale o bardzo dużej długości λ — nawet do 500 km (zwykłe fale na Oceanie około 100 m) i osiągają prędkości nawet do 900 km/h. Fale te nazywamy tsunami. Są one dużym zagrożeniem dla osiedli ludzkich znajdujących się na brzegu do którego dociera tsunami.

Pewnie wielokrotnie mieliśmy okazję obserwować fale docierające do brzegu morza. Jeśli fale są duże ulegają załamaniu tak jak na poniższym zdjęciu:

Załamywanie się fal.

W dużym uproszczeniu w ramach rozpatrywanego przez nas wyżej modelu dla płytkiej wody funkcję falowa możemy przedstawić w postaci: [math]\Psi_y(y,z,t)\approx A\left(1+\frac yh\right)\cos(\omega t -kz)[/math], oraz jej prędkość (w kierunku rozchodzenia się fali): [math]v_z(y,z,t)\approx A\left(\frac 1{kh}\right)\omega\cos(\omega t -kz)[/math]. Łącząc oba wyrażenia oraz korzystając ze związku dyspersyjnego dla tego przypadku ([math]\omega =\sqrt{gh}k[/math] otrzymujemy:

[math]v_z\approx \frac{A\omega}{kh}\cos(\omega t -kz)=\frac{\omega}{kh}\Psi_y(0,z,t)=\sqrt\frac gh \Psi[/math]

Widzimy więc, że prędkość cząsteczek wody wzdłuż osi z zależy od ich wychylenia położenia równowagi. Cząsteczki znajdujące się na szczycie fali są bardziej wychylone niż cząsteczki znajdujące się poniżej (mają większą wartość funkcji falowej [math]\Psi_y\;[/math]) a więc mają też większą prędkość. Dlatego wyprzedzają cząsteczki znajdujące się niżej i fale załamuje się.

Na koniec rozważań do tyczących fal na wodzie należy zwrócić uwagę na bardzo ważny fakt, że prędkość fali zależy od jej długości. Dlatego miedzy innymi używaliśmy nazwy prędkość fazowa fali. Do tego zagadnienia wrócimy szerzej w następnym rozdziale.