Pracownia EEG/EEG wlasnosci EEG spoczynkowego
Spis treści
Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.
Wstęp
Z funkcjami tymi spotkaliśmy się już na zajęciach z analizy sygnałów.
Funkcja autokowariancji sygnału charakteryzuje liniową zależność wartości tego sygnału w danej określonej chwili czasu od wartości (tego samego sygnału) w innej chwili. W przypadku stacjonarnych procesów stochastycznych, przebieg tej funkcji nie zależy od czasu. Oznacza to, że obliczając funkcję autokorelacji sygnału pomiędzy chwilą czasu [math]x(t)[/math] i [math]x(t+\tau )[/math] otrzymamy tę samą wartość, jak dla przypadku obliczania funkcji autokorelacji pomiędzy momentami [math]x(t + T)[/math] i [math]x(t + T+\tau )[/math], gdzie [math]T[/math] to dowolny przedział czasu. Innymi słowy, funkcja autokorelacji procesu stacjonarnego zależy tylko od odstępu czasu pomiędzy próbkami [math]\tau[/math], dla którego jest wyznaczana, a nie od konkretnej chwili czasu. Odrębną klasę sygnałów stanowią procesy niestacjonarne, w przypadku których funkcja autokorelacji będzie zależeć od czasu [math]t[/math] w którym jest obliczana. Estymator funkcji autokowariancji uzyskuje się poprzez obliczanie iloczynów wartości sygnału [math]x[/math] w chwilach czasu [math]t[/math] czyli [math]x(t)[/math] i wartości sygnału [math]x[/math] w chwili czasu t+τ czyli [math]x(t+\tau)[/math] i uśredniając wartości iloczynów po czasie [math]T[/math]:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
gdzie:
Funkcja autokowariancji może osiągać dowolne wartości, dlatego aby można było porównać przebieg tej funkcji np. pomiędzy dwoma sygnałami, wprowadzono wersję znormalizowaną tej funkcji - funkcję autokorelacji. Normalizacja ta wygląda następująco:
gdzie:
Wariancję sygnału ([math]\gamma (0)=\sigma ^2[/math]) można wyrazić przez funkcję autokowariancji dla przesunięcia [math]\tau =0[/math]. Wynika z tego, że funkcja korelacji przyjmuje wartości z zakresu [math][-1, \, 1][/math]. Ostatecznie estymator funkcji autokorelacji można zapisać jak poniżej:
Funkcję autokorelacji estymuje się w celu określenia, w jakim stopniu wartości sygnału w danej chwili czasu wpływają na wartości sygnału w kolejnych chwilach czasu. Ma to kluczowe znaczenie przy rozpoznawaniu rodzaju procesów fizycznych odpowiedzialnego za generowanie sygnału. Funkcja ta zawsze mam maksimum dla przesunięcia [math]\tau =0[/math].
Cechą charakterystyczną funkcji autokorelacji jest to, iż w przypadku sygnałów harmonicznych, przebieg funkcji ma charakter okresowy, z okresem takim samym jak okres badanego sygnału. W przypadku szumu, funkcja autokorelacji ma kształt funkcji delta Diraca.
Polecenie:
Zaimplementuj funkcję do obliczania funkcji korelacji zgodnie ze wzorem (4). Funkcja powinna przyjmować dwa wektory i maksymalne przesunięcie wzajemne tych wektorów, natomiast zwracać powinna wektor zawierający funkcję autokorelacji. Wywołanie przykładowe:
a = np.array([1,2,3])
print koreluj(a,a,2)
powinno dać wynik:
[-0.5 0. 1. 0. -0.5]
Zadanie 1: Funkcje autokowariancji i autokorelacji
W tym zadaniu posłużymy się sygnałami zarejestrowanymi w punkcie 3. poprzedniego ćwiczenia. Zaobserwuj, na którym kanale rytm alfa osiąga najwyższą wartość. Następnie zaimplementuj w Pythonie następujące kroki:
- Wczytaj dane z wybranego kanału.
- Oblicz funkcję autokorelacji dla sygnału zarejestrowanego w warunkach, gdy osoba badana siedziała z otwartymi oczami. Narysuj autokorelogram, to jest wykres wartości funkcji autokorelacji względem przesunięcia [math]\tau [/math]. Oś [math]\tau [/math] wyskaluj w sekundach.
- Powtórz krok 2, tym razem za sygnału zebranego w warunkach czuwania z zamkniętymi oczami.
- Porównaj autokorelogramy.
Związek autokorelacji z widmem sygnału
Wstęp
Zgodnie z twierdzeniem Chinczyna, z którym zapoznaliśmy się na wykładzie z Analizy Sygnałów, widmową gęstość mocy sygnału można policzyć jako transformatę Fouriera funkcji autokowariancji:
gdzie:
- [math]f[/math] — częstość
- [math]S(f)[/math] — gęstość widmowa mocy
Polecenie 1
Zaimplementuj funkcję obliczającą transformatę Fouriera dyskretyzując wzór (9) dla zadanego wektora częstości f i zadanej częstości próbkowania sygnału (tutaj 10.0):
Wywołanie przykładowe:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,1)
X,f = fourier(x,f,10.0)
print X
Powinno dać:
[ 3.15975012e-16 +5.19678720e-16j 1.05325004e-16 +3.51083347e-16j -4.56408351e-16 -2.10650008e-16j 4.91516686e-16 +1.58113883e+00j -1.40433339e-16 -7.02166694e-17j 0.00000000e+00 +0.00000000e+00j -1.40433339e-16 +7.02166694e-17j 4.91516686e-16 -1.58113883e+00j -4.56408351e-16 +2.10650008e-16j 1.05325004e-16 -3.51083347e-16j]
Natomiast wywołanie:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,0.01)
X = fourier(x,f,10.0)
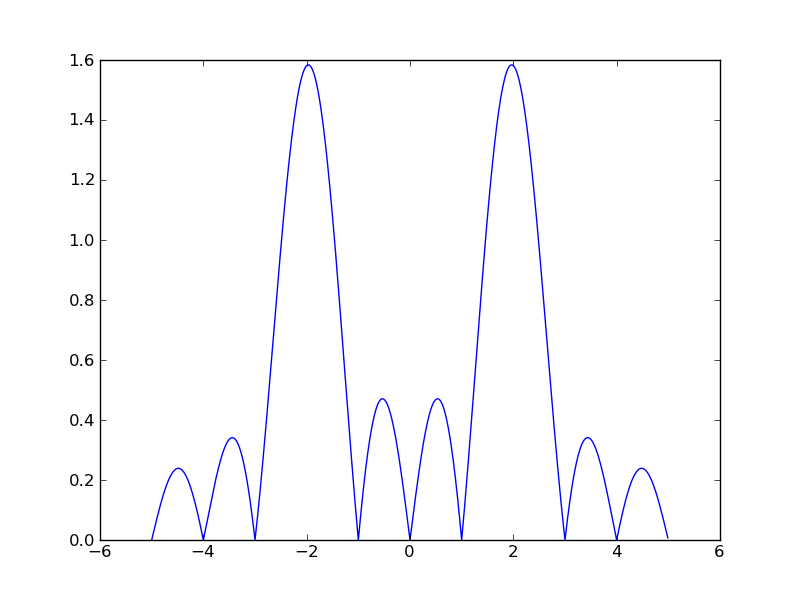
py.plot(f,np.abs(X))
py.show()
Powinno wytworzyć rysunek:
Zadanie 2: Związek autokorelacji z widmem sygnału
Oblicz gęstość widmową mocy sygnału zarejestrowanego w trakcie czuwania z zamkniętymi oczami, korzystając z twierdzenia Chinczyna oraz metodą Welcha. Znajdź częstość rytmu [math]\alpha[/math] dla osoby, która była badana.
Wzajemna gęstość widmowa sygnałów i koherencja
Zadanie 4: Wzajemna gęstość widmowa sygnałów i koherencja
Wstęp
Podobnie jak w przypadku twierdzenia Chinczyna dla pojedynczego sygnału, możliwe jest policzenie transformaty Fouriera funkcji kowariancji. Uzyskana w ten sposób wielkość nazywa się funkcją wzajemnej gęstości mocy widmowej sygnału:
W celu dalszego omówienia własności funkcji wzajemnej mocy widmowej sygnałów funkcję tę zapiszemy w postaci:
Wartość bezwzględna funkcji wzajemnej gęstości mocy widmowej osiąga największą wartość dla częstości, w których sygnały [math]x(t)[/math] i [math]y(t)[/math] są ze sobą skorelowane. Funkcja wzajemnej mocy widmowej sygnałów pozbawiona jest zatem wady, która charakteryzowała funkcję korelacji, to jest problemu z wyznaczeniem czasu transmisji sygnału, w przypadku gdy czas ten zależał od częstości. Przy pomocy funkcji wzajemnej mocy widmowej, czas ten można oszacować przy pomocy fazy tej funkcji — [math]\phi _{xy}(f)[/math]. Jeśli funkcja wzajemnej mocy widmowej została wyznaczona pomiędzy sygnałami na wejściu i wyjściu układu liniowego, to faza ta reprezentuje przesunięcie fazowe sygnału przy przejściu przez układ. Czas tego przejścia można oszacować za pomocą następującej wyrażenia:
Podobnie jak w przypadku funkcji autokorelacji i korelacji wzajemnej, funkcję wzajemnej gęstości mocy widmowej można znormalizować:
Znormalizowaną postać funkcji wzajemnej gęstości mocy widmowej nazywamy funkcją koherencji. Koherencja jest wielkością zespoloną. Faza koherencji odzwierciedla różnicę faz pomiędzy dwoma sygnałami. Moduł koherencji reprezentuje stopień synchronizacji sygnałów i zawiera się w przedziale od 0.0 do 1.0. Moduł tej funkcji zawiera się w przedziale od 0 do 1. Wartości 0 odpowiada brak synchronizacji pomiędzy sygnałami, zaś wartości 1 pełna synchronizacja dwóch przebiegów czasowych. Należy również zwrócić uwagę na nazewnictwo - często sam moduł koherencji określany jest jako koherencja, w literaturze anglojęzycznej moduł koherencji posiada jednak odrębną nazwę: Magnitude Square Coherence (MSC). Istotny jest również sposób estymacji modułu koherencji, który wyprowadzono w następnym rozdziale, zaś sam estymator reprezentuje wzór (36).
Kilka słów o koherencji
Wzór (Equation 13), definiujący ilościową miarę koherencji, nie uwzględnia stochastycznego charakteru sygnałów. Łatwo zauważyć, że bezpośrednie zastosowanie tego wzoru do obliczenia koherencji dwóch sygnałów o tej samej częstości i różniących się jedynie amplitudą oraz fazą, zawsze da wynik równy 1. Prześledźmy to na następującym przykładzie.
Dane są dwa sygnały harmoniczne [math]x(t) = A\cos(\Omega t + \phi_x)[/math] oraz [math]y(t) = B\cos(\Omega t + \phi_y)[/math].
Widmo tych sygnałów, wyrażone za pomocą transformaty Fouriera, będzie miało następującą postać:
[math]X(f)=Ae^{-j\phi_x}[/math]
[math]Y(f)=Be^{-j\phi_y}[/math],
zaś ich widmo wzajemne:
[math]X(f)\cdot Y^*(f) = A\cdot Be^{-j(\phi_x - \phi_y)}[/math],
gdzie: [math]j=\sqrt{-1}[/math], a * oznacza sprzężenie liczby zespolonej.
Podstawienie wyrażeń na widmo sygnałów [math]x(t)[/math], [math]y(t)[/math] oraz ich widmo wzajemne do wzoru ??? da koherencję [math]K_{xy}(f) = 1[/math] niezależnie od amplitudy sygnałów [math]A[/math] i [math]B[/math] oraz ich faz [math]\phi_x[/math] i [math]\phi_y[/math].
W praktyce rzadko jednak mamy do czynienia z sygnałami harmonicznymi. Zwykle mierzone przez nas wielkości mają stochastyczny charakter bądź też ich pomiar jest zaburzany przez różne czynniki.
Rozważmy teraz najprostszy model pomiaru sygnału, w którym uwzględniono wpływ zakłóceń w postaci białego szumu. Na wejście układu LTI o funkcji impulsowej opisanej wyrażeniem [math]h(t)[/math] podamy sygnał [math]x(t)[/math] i widmie danym funkcją [math]X(f)[/math]. Układ LTI przetworzy sygnał wejściowy na przebieg [math]y(t)[/math] o widmie [math]Y(f)[/math]. Z uwagi na zaburzenia [math]n(t)[/math] o widmie [math]N(f)[/math] towarzyszące pomiarowi aparatura nie zarejestruje sygnał [math]y(t)[/math] lecz [math]z(t) = y(t) + n(t)[/math]. Opisane zależności możemy opisać za pomocą poniższych wzorów:
[math]y(t) = h(t)*x(t)[/math]
[math]z(t) = y(t) + n(t)[/math]
gdzie: [math]*[/math] - operacja splotu.
Dokonując transformacji powyższych wzorów do dziedziny częstości dostajemy:
[math]Y(f) = H(f)X(f)[/math]
[math]Z(f) = Y(f) + N(f)[/math]
gdzie: [math]H(f) = \textrm{FFT}\left\{h(t)\right\}[/math].
Wzory te można zapisać w postaci jednej zależności:
Załóżmy teraz, że w celu redukcji składowej losowej [math]n(t)[/math] wielokrotnie powtarzamy w tych samych warunkach pomiar sygnału [math]z(t)[/math]. Za każdym razem na wejściu układu LTI występuje ten sam sygnał [math]x(t)[/math]. Układ LTI również przetwarza sygnał wejściowy w ten sam sposób, jednak z uwagi na stochastyczny charakter zakłóceń, otrzymujemy kolejne różniące się do siebie przebiegi [math]z_i(t)[/math]. Niech liczbę powtórzeń pomiaru wynosi [math]K[/math]. Możemy napisać [math]K[/math] równań opisujących relację pomiędzy sygnałem wejściowym, wyjściowym i mierzonym:
Przemnóżmy teraz równania (Equation 15) obustronnie przez sprzężone widmo sygnału rejestrowanego [math]Z(f)[/math]. Dla uproszczenia zapisu operacji dokonamy na jednym, dowolnie wybranym [math]i[/math]-tym równaniu:
Na równaniu (Equation 16) dokonamy kolejno następujących przekształceń:
Dokonajmy teraz uśredniania (Equation 18) po kolejnych powtórzeniach pomiaru.
Zakładamy, że szum [math]N(f)[/math] jest nieskorelowany z sygnałem wejściowym, w związku z czym w wyniku uśredniania dwa ostatnie składniki równania (Equation 19) zostaną zredukowane: [math]\left\langle H(f)X(f)N_i^*(f)\right\rangle \approx 0 [/math], [math]\left\langle N_i(f)H^*(f)X^*(f)\right\rangle \approx 0 [/math]. Założyliśmy również za każdym razem na wejściu układu liniowego pojawia się ten sam sygnał [math]x(t)[/math], sam układ zaś nie zmienia swoich właściwości, w zwiazku z czym: [math]\left\langle|H(f)|^2|X(f)|^2\right\rangle = |H(f)|^2|X(f)|^2 [/math]. Ostatecznie uzyskaliśmy następującą zależność:
Dokonajmy kolejnego przekształcenia równania (Equation 15). tym razem przemnożymy obustronnie każde równanie przez sprzężone widmo sygnału wejściowego. W celu uproszczenia zapisu, operację tę wykonamy tylko na jednym dowolnie wybranym [math]i[/math]-tym równaniu:
,
gdzie: [math]Z_i(f)X^*(f)[/math] - to widmo wzajemne sygnałów [math]x(t)[/math] i [math]y(t)[/math]. Proste przekształcenie równania (Equation 21) prowadzi do następującego wyrażenia:
Uśrednimy teraz równanie (Equation 22) po kolejnych realizacjach pomiaru oraz obliczmy moduł uzyskanego wyniku:
Brak korelacji pomiędzy szumem [math]n(t)[/math] a sygnałem wejściowym [math]x(t)[/math] powoduje, że w wyniku uśredniania zostaje zredukowany drugi składnik równania (Equation 23): [math]\left\langle N_i(f)X^*(f)\right\rangle \approx 0[/math]. Ostatecznie uzyskujemy następującą zależność:
która wraz z równaniem (Equation 20) tworzy układ równań opisujących relacje pomiędzy widmami i widmami mocy sygnałów występujących w naszym modelu:
- [math] \left\langle|Z_i(f)|^2\right\rangle= |H(f)|^2 |X(f)|^2 + \left\langle|N_i(f)|^2\right\rangle [/math]
Z pierwszej zależności równania (Equation 25) wyznaczmy funkcję przejścia [math]|H(f)|[/math]:
[math]|H(f)| = \frac{|\left\langle Z_i(f)X^*(f)\right\rangle|}{|X(f)|^2}[/math]
i podstawy do drugiego równania układu (Equation 25). Otrzymujemy:
Równanie (Equation 26) możemy przekształcić do postaci:
a następnie do zależności:
Wyrażenie:
nazywana jest Magnitude Square Coherence pomiędzy sygnałami [math]x(t)[/math] i [math]z(t)[/math]. W przypadku, gdy wielkość ta jest równa 1 sygnały [math]x(t)[/math] i [math]z(t)[/math] są w pełni zsynchronizowane. Wielkość tę uzyskaliśmy dla sygnału na wejściu układu LTI oraz sygnału mierzonego na wyjściu. Funkcję MSC można jednak stosować do dowolnych dwóch sygnałów stochastycznych [math]x(t)[/math] i [math]y(t)[/math] przy założeniu, że istnieją pomiędzy nimi liniowe zależności:
gdzie: [math]\lt \gt [/math] - oznacza wartość średnia, [math]X_i(f), Y_i(f) [/math] to zespolone widma (policzone np. za pomocą Transformaty Fouriera), wyznaczone odpowiednio dla sygnałów X oraz Y w "i-tej" realizacji eksperymentu lub w "i-tym" oknie czasowym, na który te sygnały zostały podzielone. Wzór (36) reprezentuje estymator wartości bezwzględnej koherencji. Opierając się na podobnym co wyżej rozumowaniu, można wyprowadzić estymator funkcji koherencji, o następującej postaci:
Faza koherencji umożliwia nam estymację przesunięcia fazowego pomiędzy sygnałami X i Y, zaś moduł podniesiony do kwadratu funkcji C to MSC.
Polecenie 2
Zaimplementuj funkcję obliczającą koherencję dla pary kanałów. Oblicz i narysuj funkcję koherencji dla kolejnych par kanałów (tych samych co w zadaniu 3). Wyniki zaprezentuj w postaci kwadratowej macierzy rysunków. Ponieważ koherencja jest funkcją zespoloną, dobrze jest zaprezentować osobno jej wartość i fazę. Uzyskane wartości bezwzględne koherencje narysuj nad przekątną tej macierzy, a fazę pod przekątną. W celu obliczenia modułu koherencji i jej fazy wykorzystaj wzór 36 (wygenerowane sygnały należy podzielić na pewną liczbę odcinków)