STATLAB/Zadanie domowe

Przygotowanie danych

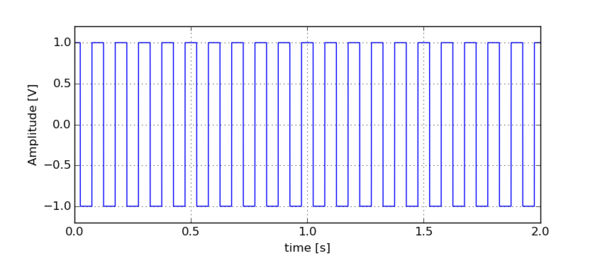
Wygneruj sygnał o długości 2 sekund i przebiegu prostokątnym, zadanym wzorem:

[math] x(t)=sgn( cos (2 \pi⋅f⋅t)) [/math]

gdzie [math]sgn[/math] to funkcja signum, zaś częstośc f jest równa 10 Hz. Sygnał wygeneruj z częstością próbkowania 192 000 Hz. Przebieg takiego sygnału zaprezentowano na rysunku poniżej:

Przepróbkowanie sygnału

Dokonaj przebrókowania sygnału do częstosci 750 Hz (repróbkowanie 256 razy), przeprowadzając je na dwa sposoby:

Metoda A: jednokrotne

Repróbkowania dokonaj w jednym kroku. W tym celu zaprojektuj filtr typu butter rzędu 3. Częstość odcięcia ustaw w częstosci Nyquista docelowej częstości próbkowania. Dobierz maksymalny możliwy rząd, zapewniejacy działanie filtru. Przefiltruj oryginalny sygnal, a następnie wybierz z przefiltrowanego sygnału co 256 próbkę.

Metoda B: Wielokrotne

Repróbkowania dokonaj w następujących krokach:

1. Przefiltruj sygnał filtrem typu butter rzędu 3 i częstości odcięcia czterokrotnie niższej niż biezaca częstości próbkowania (w pierwszym wywołaniu tej procedury częstość próbkowania wynosi 192 000 Hz, częstość odcięcia 48 000).
2. Ustaw w filtrze butter nową częstość próbkowania, która będzie równa częstości odcięcia wybranej w kroku a). Nowa częstość odciecia będzie równa ¼ nowej częstości próbkowania.
3. Powtórz krok B.1) i B.2) z nowymi częstosciami próbkowania i nowymi częstościami odcięcia aż uzyskasz częstość próbkowania 750 Hz.
4. Wybierz z przefiltrowanego na końcu sygnału co 256 próbkę.

Prezentacja wyniku i analiza

Narysuj:

1. Charakterystyki amplitudowe i fazowe zaprojektowanych w metodzie A i B filtrów.
2. Narysuj sygnał oryginalny oraz sygnały repróbkowane metodami A i B.
3. Narysuj widma amplitudowe sygnałów repróbkowanych metodami A i B.
4. Która metoda repróbkowania dała lepszy wynik ? Uzasadnij wybór.