Uczenie maszynowe i sztuczne sieci neuronowe/Wykład Ocena jakości klasyfikacji

Ocena klasyfikatorów binarnych

Klasyfikatory binarne to te, których zadaniem jest przypisanie danemu przykładowi jednej z dwóch możliwych klas. Przykładem takiego klasyfikatora jest znana już nam regresja logistyczna.

Jako przykład roboczy rozważmy problem klasyfikowania kandydatów na studia na przyjętych i nie przyjętych na podstawie wyników z dwóch egzaminów maturalnych (każdy przeskalowany na zakres 0-100%): z matematyki i z biologii. Zakładamy, że mamy dane zawierające zarówno wyniki owych egzaminów {B,M} jak i faktyczny wynik postępowania rekrutacyjnego W dla pewnej grupy osób (W może mieć dwie wartości: przyjęty, nie przyjęty). Mamy też pewien klasyfikator, który realizuje odwzorowanie: [math] G(B,M) \rightarrow K [/math] I tu podobnie, wynik klasyfikatora K może przyjąć jedną z dwóch wartości: przyjęty lub nie przyjęty.

Typy błędów

Porównując wyniki W i K możemy mieś cztery sytuacje:

		Stan faktyczny		Razem
		przyjęty	nie przyjęty
wynik klasyfikacji	przyjęty	TP	FP (błąd: wynik fałszywie pozytywny)	P'
	nie przyjęty	FN (błąd: wynik fałszywie negatywny)	TN	N'
Razem		P	N

Anglojęzyczna nomenklatura często stosowana do opisu tych możliwości to:

• TP: true positive, hit
• TN: true negative, correct rejection
• FP: false positive, false alarm, Type I error
• FN: false negative, with miss, Type II error

Miary oparte na tych definicjach to:

• czułość (inne spotykane nazwy: sensitivity, true positive rate TPR, hit rate, recall)

[math]TPR = TP / P = TP / (TP+FN)[/math]

• częstość fałszywych alarmów ( false positive rate (FPR), fall-out)

[math]FPR = FP / N = FP / (FP + TN)[/math]

• dokładność ( accuracy (ACC))

[math]ACC = (TP + TN) / (P + N)[/math]

• specyficzność: (specificity (SPC), True Negative Rate)

[math]SPC = TN / N = TN / (FP + TN) = 1 - FPR [/math]

• precyzja: (positive predictive value (PPV), precision)

[math]PPV = TP / (TP + FP)[/math]

• negative predictive value (NPV)

[math]NPV = TN / (TN + FN)[/math]

• częstość fałszywych odkryć: (false discovery rate (FDR))

[math]FDR = FP / (FP + TP)[/math]

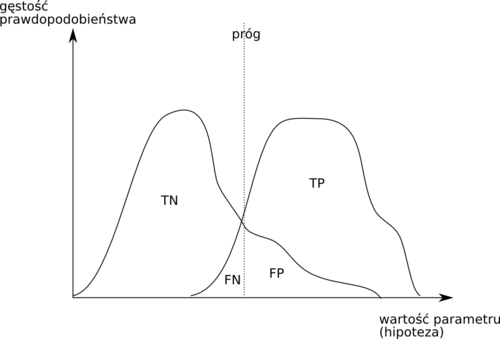
Prawdopodobieństwa podejmowania każdego rodzaju decyzji będą się zmieniały wraz z przesuwaniem progu podejmowania decyzji, czyli wartości hipotezy przy której zaliczamy przypadek do klasy 1.

Krzywe charakterystyki roboczej odbiorcy (ROC)

Krzywa ROC

każdy punkt na tej krzywej otrzymywany jest dla ustalonej wartości progu i ma współrzędne (1−specyficzność, czułość).

Krzywa ROC przydaje się do porównywania różnych klasyfikatorów oraz do wyboru punktu pracy (progu)

Kross-walidacja

Generalizacja: O co tu chodzi?

Schemat ilustrujący koncepcję generalizacji

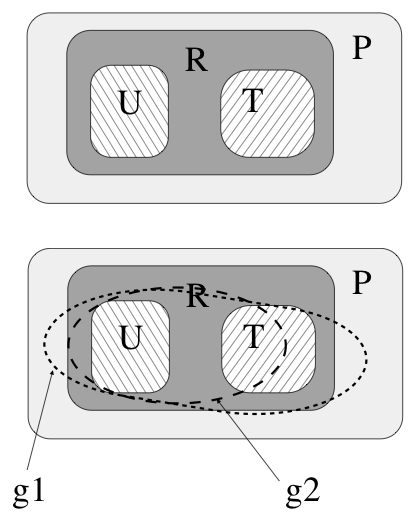
Na rysunku obok przedstawiona jest schematycznie koncepcja generalizacji. Wyobraźmy sobie, że jest pewna przestrzeń P, która zawiera pary, np. liczb {((a,b), c)}. W tym przykładzie jest to przestrzeń wszystkich odwzorowań [math]\mathcal{R}^2 \rightarrow \mathcal{R}[/math]. Niektóre z tych par reprezentują pewną konkretną relację R: np. są to pary spełniające warunek [math]c=\sqrt{a^2 +b^2}[/math]. Wyobraźmy sobie dalej, że mamy dane dwa skończone zestawy par, które tą relację spełniają, ale oczywiście nie są w stanie obejmować wszystkich możliwych par. Jeden z nich oznaczymy U, a drugi T. Załóżmy, że mamy dwie wersje sieci, które uczymy na zbiorze U (mogą się one różnić architekturą, albo punktem startu procedury uczącej, albo ilością iteracji algorytmu uczącego itp.). Po procesie uczenia sieci te mają mały i porównywalny błąd na zbiorze U, ale jedna z nich nauczyła się relacji wskazanej na rys. jako g1 a druga relacji g2. Na podstawie rezultatów odtwarzania przykładów ze zbioru testowego mówimy, że sieć druga ma lepszą generalizację niż sieć pierwsza.

Porównywanie klasyfikatorów na podstawie błędów generalizacji.

Najlepiej byłoby mieć możliwie mały błąd generalizacji — jak go oszacować? Można zastosować następujące techniki:

• wiele zbiorów testowych: trzeba mieć dużo danych, żeby wystarczyło na rozsądny zbiór treningowy i kilka testowych
• kros-walidacja: najprostsza wersja (leave-one-out):
  • wybierz przypadek do odrzucenia
  • trenuj klasyfikator na wszystkich przypadkach oprócz tego jednego — na tym jednym oblicz błąd generalizacji
  • powtarzaj to dla każdego przypadku
    Zaleta — można efektywnie użyć całego zbioru danych do uczenia i testowania,
    Cena — wielokrotne uczenie sieci
• Bootstrapowanie — wielokrotnie losuje się z powtórzeniami z pełnego zbioru dwie próby:
  • do nauki klasyfikatora
  • do testowania.