Uczenie maszynowe i sztuczne sieci neuronowe/Wykład 1

Uczenie maszynowe

Na tych zajęciach zapoznamy się z koncepcjami "uczenia maszynowego". Podejście to jest nieco odmienne od standardowego programowania. Algorytmy, które będziemy omawiać bardziej stanowią "metodologię uczenia" niż sposoby kodowania rozwiązań konkretnych problemów. Zobaczymy jak łącza się pojęcia ze statystyki, algebry z inspiracjami biologicznymi.

Na wstępie warto może wspomnieć, że uczenie może przebiegać z nadzorem lub bez nadzoru. Uczenie z nadzorem przypomina typowe uczenie w szkole, gdzie nauczyciel podaje przykłady dla których znane są prawidłowe odpowiedzi i potrafi uczniowi wskazać błędy. Uczenie bez nadzoru przypomina nieco uczenie się postrzegania świata przez małe dziecko. Bazuje ono głównie na obserwowaniu związków przyczynowo skutkowych - korelacji - pomiędzy różnymi bodźcami.

Uczenie z nadzorem

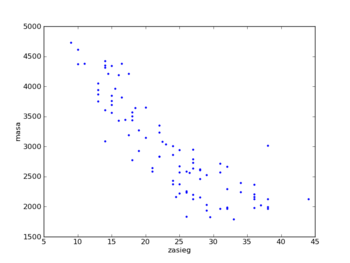
Zaczniemy od najprostszej wersji uczenia z nadzorem jaką jest regresja liniowa. Aby było nam łatwiej ją sobie wyobrażać weźmy konkretny przykład: chcielibyśmy przewidywać zużycie paliwa przez samochody. Załóżmy, że znamy odległość jaką samochód może pokonać i jego masę. Możemy narysować te dane.

Przykładowe dane

Jak na podstawie tych danych można przewidzieć zasięg innych samochodów?

Można potraktować te dane jako punkty reprezentujące pewne odwzorowanie, funkcję. Najprostszą funkcję jaką moglibyśmy zaproponować to odwzorowanie liniowe.

W tym miejscu wprowadzimy kilka ważnych pojęć i notację, z której będziemy korzystać w trakcie dalszych wykładów.

wejście

w naszym przykładzie daną wejściową jest masa samochodu. Oznaczmy ją [math]x[/math]. W kontekście uczenia maszynowego dane wejściowe często nazywane są cechami (ang. features).

przestrzeń wejść

przestrzeń, z której pochodzą dane wejściowe, oznaczymy ją [math]X[/math]

wyjście

w naszym przykładzie zasięg. Oznaczymy go [math]y[/math].

przestrzeń wyjść

przestrzeń, z której pochodzą dane wyjściowe, oznaczymy ją [math]Y[/math]

przykład

para wejścia i odpowiadającego mu wyjścia: [math](x,y)[/math] stanowi pojedynczy przykład.

ciąg uczący

zbiór przykładów [math]\lbrace (x^{(i)}, y^{(i)}), \quad i = 1, \dots ,m\rbrace [/math].

hipoteza

[math]h[/math]: odwzorowanie [math]h: X\rightarrow Y[/math], które "dobrze" pasuje do przykładów ciągu uczącego.

Formalnie proces uczenia z nadzorem polega na tym, żeby mając dany ciąg uczący znaleźć funkcję [math]h[/math] taką, że jest ona dobrym predyktorem [math]y[/math] mając dany [math]x[/math].

Gdy zmiana [math]y[/math] jest ciągła problem nazywamy regresją, gdy zmienna [math]y[/math] jest dyskretna problem nazywamy klasyfikacją.

Regresja liniowa

Aby nasz przykład uczynić bardziej interesującym załóżmy, że oprócz masy pojazdu znamy także jego moc. Aby przeprowadzić uczenie z nadzorem musimy zdecydować się jak będziemy reprezentować funkcję [math]h[/math] w komputerze. Na początek załóżmy, że będzie to funkcja liniowa:

[math]h_{\theta }(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 [/math]

Parametry [math]\theta _i[/math] (zwane także wagami) parametryzują przestrzeń funkcji liniowych [math]X \rightarrow Y[/math]. Tam gdzie nie będzie to powodować niejednoznaczności zamiast [math]h_\theta (x)[/math] będziemy pisać [math]h(x)[/math]. Dla uproszczenia notacji wprowadzimy też "sztuczne" wejście [math]x_0 =1 [/math], zaś parametr [math]\theta _0[/math] nazywać będziemy obciążeniem. Stosując powyższą konwencję możemy napisać:

[math]h(x) = \sum _{i=0}^n \theta _i x_i [/math]

(u nas n = 2). Niektóre rachunki uproszczą się nam jeśli zastosujemy notację wektorową. Oznaczmy: [math]\mathbf {\theta } = [\theta _0, \dots , \theta _n]^T[/math] , [math]\mathbf {x} = [x_0, \dots ,x_n]^T[/math] (zapisaliśmy oba wektory jako transponowane bo [math]\mathbf {\theta }[/math] i [math]\mathbf {x}[/math] są wektorami kolumnowymi). Wówczas:

[math]h(x) = \sum _{i=0}^n \theta _i x_i = \mathbf {\theta }^T \mathbf {x}[/math]

Problem uczenia maszynowego polega na tym: jak mając zbiór uczący znaleźć "dobre" parametry? Aby sformalizować ten problem wyprowadzimy funkcję kosztu.

[math]J(\mathbf {\theta }) = \frac{1}{2} \sum _{i=1}^{m} \left( h_\theta (x^{(i)}) - y^{(i)} \right)^2 [/math]

(Uwaga: [math]^{(i)}[/math] to indeks przykładu a nie potęga. ) Teraz możemy powiedzieć, że "dobre" parametry to takie, które minimalizują funkcję kosztu.

Algorytm najmniejszych kwadratów

Chcemy znaleźć takie parametry aby zminimalizować funkcję kosztów. Zobaczmy czy zadziała następujący pomysł:

Zacznijmy od pewniej "odgadniętej" wartości początkowej. Następnie zmieniamy ją zgodnie z kierunkiem przeciwnym do gradientu funkcji kosztu.

Warto tu przypomnieć, że gradient funkcji to wektor, którego kierunek pokrywa się z kierunkiem, w którym funkcja zmienia się najszybciej, a zwrot wskazuje kierunek, w którym funkcja rośnie. Zatem jeśli wyobrazimy sobie funkcję jako pofałdowany teren, to poruszając się w kierunku przeciwnym do gradientu powinniśmy dotrzeć do niżej położonych partii terenu. Formalnie jeden krok algorytmu minimalizacji gradientowej możemy zapisać:

dla każdego [math]j[/math]: [math]\theta _{j} := \theta _j - \alpha \frac{\partial }{\partial \theta _j } J(\theta ) [/math]

gdzie parametr [math]\alpha [/math] to szybkość uczenia.

Przyjrzyjmy się pochodnej cząstkowej [math]\frac{\partial }{\partial \theta _j } J(\theta ) [/math]:

[math]\begin{matrix} \frac{\partial }{\partial \theta _j } J(\theta ) &=& \frac{\partial }{\partial \theta _j } \frac{1}{2} \sum _{i=1}^{m} \left( h_\theta (x^{(i)}) - y^{(i)} \right)^2 \\ &=&\frac{1}{2} \sum _{i=1}^{m} \frac{\partial }{\partial \theta _j } \left( h_\theta (x^{(i)}) - y^{(i)} \right)^2\\ &=&\frac{1}{2} \sum _{i=1}^{m} 2 \left( h_\theta (x^{(i)}) - y^{(i)} \right)\frac{\partial }{\partial \theta _j }h_\theta (x^{(i)})\\ &=& \sum _{i=1}^{m} \left( h_\theta (x^{(i)}) - y^{(i)} \right)\frac{\partial }{\partial \theta _j } \sum _{j=0}^n \theta _j x_j^{(i)}\\ &=& \sum _{i=1}^{m} \left( h_\theta (x^{(i)}) - y^{(i)} \right) \sum _{j=0}^n \frac{\partial }{\partial \theta _j }\theta _j x_j^{(i)}\\ &=& \sum _{i=1}^{m} \left( h_\theta (x^{(i)}) - y^{(i)} \right) x_j^{(i)} \end{matrix}[/math]

Algorytm najmniejszych kwadratów ma kilka cech, które są intuicyjne i naturalne. Wartość zmiany jest proporcjonalna do błędu. Gdy mamy przykład uczący, dla którego przewidywanie prawie zgadza się z [math]y[/math] to wprowadzane zmiany parametrów są małe. Większa zmiana parametrów będzie dla przykładu, który generuje większy błąd.

Powyższe obliczenia dotyczą sytuacji gdy ciąg uczący zawierają wiele przykładów i poprawki obliczamy biorąc pod uwagę wszystkie przykłady. Jest to tak zwany algorytm gradientowy zbiorczy (ang. batch gradient descent).

Uaktualnianie parametrów funkcji kosztu można też prowadzić po każdej prezentacji elementu ciągu uczącego. Zauważmy, że w pierwszej linijce naszych przekształceń występuje suma po przyczynkach pochodzących od pojedynczych przykładów. Każdy przykład daje przyczynek dodatni. Zatem minimalizując każdy z przyczynków niezależnie również zminimalizujemy funkcję kosztu. Wersja algorytmu, w której zmiany parametrów obliczane są i dla pojedynczych przykładów z ciągu uczącego podawanych w losowej kolejności nosi nazwę stochastycznego algorytmu minimalizacji gradientowej. Ta wersja algorytmu jest zwykle bardziej wydajna obliczeniowo.

Warto w tym miejscu zauważyć, że algorytm gradientowy jest wrażliwy na minima lokalne, tzn. że z danego punktu w przestrzeni parametrów prowadzi do najbliższego minimum lokalnego. Na szczęście w przypadku regresji linowej istnieje tylko jedno minimum i jest to minimum globalne.

Równania normalne

Iteracyjna wersja minimalizacji funkcji kosztu przyda nam się jeszcze przy omawianiu algorytmów uczenia sztucznych sieci neuronowych. W pewnych sytuacjach można wykorzystać nieco bardziej narzędzia algebry i analizy matematycznej i znaleźć optymalne parametry analitycznie. W tym celu trzeba znaleźć pochodna funkcji kosztu po parametrach i przyrównać ją do zera.

Aby rachunki poszły nam sprawniej przypomnijmy kilka wzorów z algebry.

Rachunki macierzowe

Dla danej funkcji [math]f: \mathcal {R}^{n \times m} \rightarrow \mathcal {R}[/math] mapującej macierze [math]n \times m[/math] na liczby rzeczywiste definiujemy pochodną [math]f[/math] względem [math]A[/math] jako:

[math] \nabla _A f(A) = \left[ \begin{array}{ccc} \frac{\partial f}{\partial A_{1,1}} & \dots & \frac{\partial f }{\partial A_{1,n}} \\ \vdots & & \vdots \\ \frac{\partial f}{\partial A_{n,1}}& \dots &\frac{\partial f}{\partial A_{n,n}} \end{array} \right] [/math]

Zatem gradient [math]\nabla _A f(A) [/math] jest macierzą [math]n \times m[/math], której element [math](i,j)[/math] to pochodna cząstkowa [math] \frac{\partial f}{\partial A_{i,j}}[/math].

Jako przykład weźmy macierz

[math]A = \left[ \begin{array}{cc} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \end{array} \right] [/math]

i funkcję [math]f: \mathcal {R}^{n \times m} \rightarrow \mathcal {R}[/math] :

[math] f(A) = \frac{3}{2} A_{1,1} + 5 A_{1,2}^2 + A_{2,1} A_{2,2} [/math]

W tym przypadku otrzymujemy:

[math] \nabla _A f(A) = \left[ \begin{array}{ccc} \frac{3}{2} & 10 A_{1,2} \\ A_{2,2} & A_{2,1} \end{array} \right] [/math]

Dla przypomnienia operator śladu macierzy kwadratowej [math]A[/math] to suma elementów diagonalnych:

[math] \textrm {tr}A = \sum _{i=1}^{n}A_{i,i}[/math]

Operator śladu jest przemienny, tzn.

[math] \textrm {tr}AB = \textrm {tr}BA[/math]

Zachodzi również:

[math]\textrm {tr}A =\textrm {tr}A^T[/math]

[math]\textrm {tr}(A+B) =\textrm {tr}A + \textrm {tr}B[/math]

[math]\textrm {tr}(aA) = a\textrm {tr}A[/math]

Dla pochodnych macierzowych zachodzi:

[math] \nabla _A \textrm {tr}AB = B^T [/math]

[math] \nabla _{A^T} f(A) = (\nabla _A f(A))^T [/math]

[math] \nabla _A \textrm {tr} ABA^TC = CAB +C^TAB^T [/math]

[math] \nabla _A |A| = |A| (A^{-1})^T [/math]

gdzie [math]|A|[/math] to wyznacznik macierzy A.

Minimalizacja funkcji kosztu

Uzbrojeni w powyższe wzory możemy powrócić do minimalizacji funkcji kosztu. Zbudujmy macierz wejść [math]X[/math] w taki sposób, że wejścia z poszczególnych przykładów są jej wierszami.

[math]X = \left[ \begin{array}{ccc} -& ( x^{(1)})^T&- \\ & \vdots & \\ - &(x^{(m)})^T &- \end{array} \right] [/math]

Z wartości wyjściowych zbudujemy wektor kolumnowy

[math]\mathbf {y} = \left[ \begin{array}{c} y^{(1) }\\ \vdots \\ y^{(m)} \end{array} \right] [/math]

Ponieważ [math]h_\theta (x^{(i)} ) = (x^{(i)})^T \theta [/math] możemy zapisać:

[math] X \theta - \mathbf {y} = \left[ \begin{array}{c} ( x^{(1)})^T \theta \\ \vdots \\ (x^{(m)})^T \theta \end{array} \right] - \left[ \begin{array}{c} y^{(1) }\\ \vdots \\ y^{(m)} \end{array} \right] = \left[ \begin{array}{c} h_\theta (x^{(1)}) - y^{(1) }\\ \vdots \\ h_\theta (x^{(m)}) - y^{(m)} \end{array} \right] [/math]

Korzystając z faktu, że dla wektora [math]\mathbf {z}[/math] mamy [math]\mathbf {z}^T\mathbf {z}=\sum _i z_i^2[/math] możemy zapisać funkcję kosztu w następujący sposób:

[math]J(\theta ) = \frac{1}{2} \sum _{i=1}^m \left( h_\theta (x^{(i)} ) - y^{(i)}\right)^2 = \frac{1}{2} (X \theta - \mathbf {y})^T (X \theta - \mathbf {y}) [/math]

Teraz aby zminimalizować funkcję kosztu [math]J[/math] znajdzmy jej pochodną względem [math]\theta [/math]. Korzystając z równań (%i 2) i (%i 3) widzimy, że:

[math] \nabla _{A^T} \textrm {tr}ABA^TC = B^T A^T C^T + B A^T C [/math]

Tak więc:

[math]\begin{matrix} \nabla _\theta J(\theta ) &=& \nabla _\theta \frac{1}{2} (X \theta - \mathbf {y})^T (X \theta - \mathbf {y}) \\ &=& \frac{1}{2} \nabla _\theta ( \theta ^T X ^T X \theta -\theta ^T X^T \mathbf {y} - \mathbf {y}^T X \theta + \mathbf {y}^T \mathbf {y}) \\ &=& \frac{1}{2} \nabla _\theta \textrm {tr}( \theta ^T X ^T X \theta -\theta ^T X^T \mathbf {y} - \mathbf {y}^T X \theta + \mathbf {y}^T \mathbf {y}) \\ &=& \frac{1}{2} \nabla _\theta (\textrm {tr} \theta ^T X ^T X \theta - 2 \textrm {tr} \mathbf {y}^T X \theta ) \\ &=& \frac{1}{2} ( X ^T X \theta +X^T X \theta - 2 X^T \mathbf {y}) \\ &=& X^T X \theta - X^T \mathbf {y} \end{matrix}[/math]

Użyte tricki:

1. w trzecim kroku skorzystaliśmy z tego, że ślad liczby jest tą samą liczbą
2. w czwartym kroku skorzystaliśmy z tego, że [math]\textrm {tr}A = \textrm {tr}A^T[/math]
3. w piątym kroku skorzystaliśmy z równania (%i 5), podstawiając [math]A^T = \theta [/math], [math]B = B^T = X^TX[/math] i [math]C = I[/math] oraz równanie (%i 1)

Aby zminimalizować funkcję kosztu kładziemy jej pochodną równą 0 i otrzymujemy równanie normalne:

[math] X^T X \theta = X^T \mathbf {y}[/math]

Z niego możemy obliczyć parametry minimalizujące funkcję kosztu:

  [math] \theta = (X^T X )^{-1} X^T \mathbf {y}[/math]

Interpretacja probabilistyczna

Dlaczego funkcja kosztu [math]J[/math] w postaci sumy kwadratów błędów dla problemu regresji jest sensowna? W tej sekcji zaprezentuje zestaw założeń probabilistycznych, dla których kwadratowa funkcja błędu jest naturalną konsekwencją.

Załóżmy, że zmienne wejściowe i wyjściowe powiązane są zależnością:

[math] y^{(i)} = \theta ^T x^{(i)} + \epsilon ^{(i)}[/math]

gdzie [math]\epsilon ^{(i)}[/math] jest błędem, który albo pochodzi od pewnych nieuwzględnionych w modelu regresji czynników lub czynnikiem losowym. Załóżmy, że [math]\epsilon ^{(i)}[/math] to zmienne niezależne i podlegające temu samemu rozkładowi (ang. IID - independent and identically distributed) normalnemu o średniej zero i wariancji [math]\sigma ^2[/math]. To założenie zapisujemy krótko: [math] \epsilon ^{(i)} \sim \mathcal {N}(0, \sigma ^2)[/math] . Zatem funkcja gęstości prawdopodobieństwa [math]\epsilon ^{(i)}[/math] dana jest wzorem:

[math] p(\epsilon ^{(i)}) = \frac{1}{\sqrt{2 \pi} \sigma } \exp \left( - \frac{ \left(\epsilon ^{(i)} \right)^2}{2 \sigma ^2} \right) [/math]

Z tego wynika, że:

[math] p(y^{(i)}| x^{(i)}; \theta ) = \frac{1}{\sqrt{2 \pi} \sigma } \exp \left( - \frac{ \left(y^{(i)} - \theta ^Tx^{(i)} \right)^2}{2 \sigma ^2} \right) [/math]

Notacja [math]p(y^{(i)}| x^{(i)}; \theta )[/math] oznacza funkcję gęstości prawdopodobieństwa zmiennej [math]y^{(i)}[/math] mając daną zmienną [math]x^{(i)}[/math] sparametryzowaną przez [math]\theta [/math]. Nie mówimy "mając dane [math]\theta [/math]" bo [math]\theta [/math] nie jest zmienną losową. Prawdopodobieństwo danych (całego ciągu uczącego) określone jest przez rozkład [math]p(\mathbf {y}|X;\theta )[/math]. Ten rozkład zazwyczaj rozumiany jest jako funkcja [math]\mathbf {y}[/math] i [math]X[/math] przy ustalonym [math]\theta [/math]. Możemy jednak spojrzeć na niego inaczej, tzn. jako funkcję [math]\theta [/math] przy ustalonych [math]X[/math] i [math]\mathbf {y}[/math]. Funkcję tą nazywamy funkcją wiarygodności:

[math]L(\theta ) = L(\theta ;X,\mathbf {y}) = p(\mathbf {y}|X;\theta )[/math]

Zauważmy, że dzięki założeniu o niezależności [math]\epsilon ^{(i)}[/math] możemy tą funkcję zapisać jako:

[math]\begin{matrix} L(\theta ) &=& \prod _{i=1}^m p(y^{(i)} | x^{(i)};\theta )\\ &=& \prod _{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma } \exp \left( - \frac{ \left(y^{(i)} - \theta ^Tx^{(i)} \right)^2}{2 \sigma ^2} \right) \end{matrix}[/math]

Teraz, mając nasz model probabilistyczny możemy się zapytać: jakie [math]\theta [/math] są sensowne? Chcielibyśmy, aby były to takie parametry, dla których zaobserwowanie naszego ciągu uczącego jest najbardziej prawdopodobne. Jest to zasada największej wiarygodności. A zatem w myśl tej zasady trzeba znaleźć [math]\theta [/math], które maksymalizuje funkcję wiarygodności [math]L(\theta )[/math]. Tak naprawdę wystarczy jeśli zmaksymalizujemy dowolną ściśle rosnącą funkcję funkcji wiarygodności. Rachunki znacznie się uproszczą jeśli jako tą funkcję wybierzemy [math]\log [/math] (wówczas iloczyn przejdzie w sumę). Ostatecznie chcemy zmaksymalizować:

[math]\begin{matrix} l(\theta ) &=& \log (L(\theta )) \\ &=& \log \prod _{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma } \exp \left( - \frac{ \left(y^{(i)} - \theta ^Tx^{(i)} \right)^2}{2 \sigma ^2} \right)\\ &=& \sum _{i=1}^m \log \frac{1}{\sqrt{2 \pi} \sigma } \exp \left( - \frac{ \left(y^{(i)} - \theta ^Tx^{(i)} \right)^2}{2 \sigma ^2} \right) \\ &=& m \log \frac{1}{\sqrt{2 \pi }\sigma } - \frac{1}{\sigma ^2} \cdot \frac{1}{2} \sum _{i=1}^m \left( y^{(i)} - \theta ^Tx^{(i)} \right)^2 \end{matrix}[/math]

Zauważmy, że aby zmaksymalizować funkcję wiarygodności musimy zminimalizować wyrażenie [math] \frac{1}{2} \sum _{i=1}^m \left( y^{(i)} - \theta ^Tx^{(i)} \right)^2 [/math], czyli wprowadzoną w poprzednim rozdziale funkcję kosztu [math]J(\theta )[/math].

Podsumowując: zakładając konkretny model probabilistyczny ciągu uczącego udało nam się pokazać, że minimalizacja funkcji kosztu jest konsekwencją zastosowania zasady największej wiarygodności. Warto jednak pamiętać, że procedura minimalizacji średniego błędu kwadratowego daje sensowne wyniki dla znacznie szerszej klasy modeli danych.