Uczenie maszynowe i sztuczne sieci neuronowe/Ćwiczenia 4

Algorytm wstecznej propagacji błędu

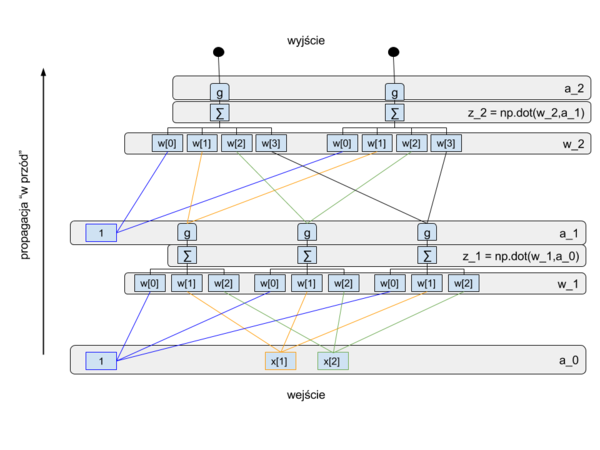
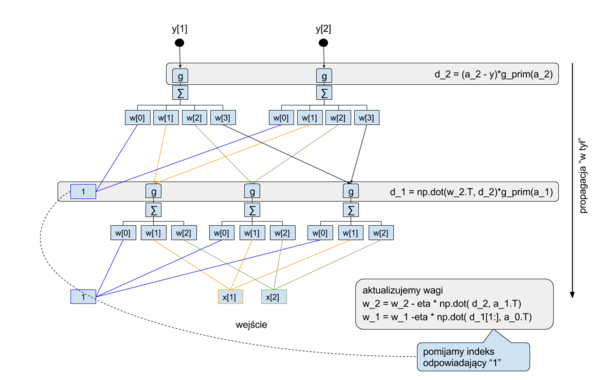
W tym ćwiczeniu zapoznamy się z algorytmem wstecznej propagacji błędu. Zbudujemy sieć złożoną z 3 warstw: wejściowej, ukrytej i wyjściowej. Schemat obliczeń wykonywanych przez tą sieć przedstawiony jest na poniższych rysunkach:

Schemat obliczeń w propagacji wstecznej

Schemat obliczeń w propagacji wstecznej

Warstwy ukryta i wyjściowa będą miały nieliniową funkcję aktywacji w postaci funkcji logistycznej. Dla przypomnienia funkcja logistyczna:

[math]g(x) = \frac{1}{1+exp(-x)}[/math]

zaś jej pochoną to:

[math]g'(x) =g(x)*(1-g(x)) [/math]

Niech nasza sieć uczy się odwzorowania zadanego tabelką:

X	Y
[0,0]	[0,1]
[0,1]	[1,0]
[1,0]	[1,0]
[1,1]	[0,1]

Proszę napisać kod implementujący obliczenia przedstawione na rysunkach i w poniższym opisie:

• zdefiniuj funkcję g(x)
• zdefiniuj funkcję pochodną g_prim(y), zakładając, że jako argument y podawać będziemy wartość g(x)
• przygotuj zbiór uczący zgodnie z powyższą tabelą. Niech przykłady będą ułożone w wierszach tablic X i Y
• zdefiniuj rozmiary sieci:
  • N_wej
  • N_hid
  • N_wyj
• przygotuj tablicę do przechowywania wag w_1, niech w kolejnych wierszach znajdują się wagi kolejnych neuronów, a w konkretnym wierszu w kolumnach kolejne wagi od konkretnego neuronu
  • jakie rozmiary muszą mieć te tablice?
  • zainicjuj je wartościami losowymi z przedziału -1,1
• podobnie przygotuj tablicę dla wag w_2
• w pętli wykonuj kolejne cykle uczenia
  • zainicjuj do zera: licznik błędu wyjściowego bl, oraz tablice akumulujące delty do zmiany wag D_1 i D_2
  • w pętli pobieraj kolejno przykłady. Pobierając przykłady formuj je jako wektory kolumnowe
    • propaguj sygnały od wejścia:
      • uzupełnij wektor wejściowy o "1" na szczycie, wsk. np.vstack)
      • oblicz pobudzenia neuronów z_1,
      • oblicz wartości wyjściowe z warstwy ukrytej
      • uzupełnij wektor wartości wyjściowych warstwy ukrytej o "1"
      • oblicz pobudzenia w warstwie wyjściowej
      • oblicz wartości wyjściowe z tej warstwy
    • propaguj błędy "wstecz"
      • oblicz błąd warstwy wyjściowej ważony przez pochodną funkcji g (im bardziej funkcja g była stroma w miejscu pobudzenia przy propagacji wprzód, tym bardziej błąd pobudzenia przekładał się na błąd wyjścia)
      • zrzutuj ten błąd wstecz poprzez wagi w_2 i pochodną funkcji g
      • akumulujemy poprawki D_1 i D_2 oraz błąd dla tego przykładu
  • uaktualniamy wagi proporcjonalnie do poprawek (z przeciwnym znakiem)
  • wypisujemy info o błędzie

XOR

Jako pierwszy przykład z zastosowania sieci nieliniowych proszę skonstruować sieć z jedną warstwą ukrytą, rozwiązującą problem XOR.

Potrzebne nam będą następujące importy:

from pybrain.datasets.supervised import SupervisedDataSet
from pybrain.tools.shortcuts import buildNetwork
from pybrain.supervised.trainers import BackpropTrainer, RPropMinusTrainer
from pybrain.structure import  LinearLayer,SigmoidLayer

• do stworzenia ciągu uczącego proszę wykorzystać funkcje addSample obiektu SupervisedDataSet:

ZU = SupervisedDataSet(N_wej,N_wyj)
ZU.addSample((0,0),(0.0,))
ZU.addSample((0,1),(1.0,))
ZU.addSample((1,0),(1.0,))
ZU.addSample((1,1),(0.0,))

• W konstrukcji sieci proszę wykorzystać funkcję: buildNetwork, tak aby wszystkie warstwy były sigmoidalne:

siec = buildNetwork(N_wej, N_hid, N_wyj, outclass=SigmoidLayer)

• Proszę zbadać strukturę wytworzonej sieci:

siec['in']
siec['hidden0']
siec['out']

• sieć uczymy metodą wstecznej propagacji błędu, za pomocą funkcji train obiektu BackpropTrainer. Funkcja ta wykonuje jeden cykl uczenia (jednorazowe przejście przez ciąg uczący, przykłady podawane są w losowej kolejności) i zwraca wartość średniego błędu średniokwadratowego w tym cyklu.

• Proszę wykreślić ewolucje wag i błędu. Ewolucję można zilustrować animacją. W tym celu na początku programu należy ustawić backend dla biblioteki matplotlib przed innymi importami i przełączyć grafikę w tryb interaktywny:

import matplotlib
matplotlib.use('TkAgg')
import pylab as py
py.ion()

Następnie animację robimy analogicznie jak w tym przykładzie.

• Proszę zbadać co dzieje się z wagami wraz ze wzrostem ilości jednostek w warstwie ukrytej.
• Proszę zbadać jak zmienia się zbieżność algorytmu przy zmianie moetody uczenia na Elastyczną propagację wsteczna.

Uwaga

w przypadku trenera RPropMinusTrainer należy podać zbiór uczący za pomocą metody setData().

• Proszę powtórzyć analizę dla sieci, której warstwa wyjściowa ma jednostkę liniową.
• Proszę zbadać wpływ regularyzacji (weightdecay w BackpropTrainer) na strukturę sieci.

Przykładowe rozwiązanie: 

import matplotlib
matplotlib.use('TkAgg')

from pybrain.datasets.supervised import SupervisedDataSet
from pybrain.tools.shortcuts import buildNetwork
from pybrain.supervised.trainers import BackpropTrainer
import numpy as np
import pylab as py

N_wej = 2
N_wyj = 1
ZU = SupervisedDataSet(N_wej,N_wyj)
ZU.addSample((0,0),(0.2,))
ZU.addSample(...)
ZU.addSample(...)
ZU.addSample(...)

N_hid = ...
siec = buildNetwork(...)

t = BackpropTrainer(siec, ZU, learningrate=0.05, momentum=0.95, verbose=False)  # dodatkowe parametry sterujące przebiegim uczenia:  lrdecay=1.0, weightdecay=0.0025)

N_krokow = 1000
err = np.zeros(N_krokow)
wagi = np.zeros((N_krokow,len(siec.params)))

py.ion()
py.subplot(2,1,1)
l_err, = py.plot(err)
py.ylim([0,1])
py.subplot(2,1,2)
l_wagi = py.plot(wagi)
py.ylim([-3,3])

for i in range(N_krokow):
    err[i] = t.train()
    wagi[i,:] = ...
    l_err.set_ydata(err)
    for k in range(len(l_wagi)):
        l_wagi[k].set_ydata(wagi[:,k])
    py.draw()

print '0','0','->', str(siec.activate((0,0)))
print '0','1','->', str(siec.activate(...))
print '1','0','->', str(siec.activate(...))
print '1','1','->', str(siec.activate(...))
py.ioff()
py.show()