Laboratorium EEG/Analiza czas-częstość w matlabie

Z Brain-wiki

Laboratorium_EEG/Czas-częstość


Moduł czas-częstość w Matlabie

Zasada nieoznaczoności dla przestrzeni czas-częstość

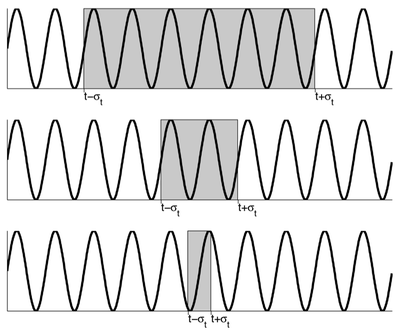
Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość.

Zasada nieoznaczonosci tf.png

Zasadę tą można wyrazić formalnie w następujący sposób. Potraktujmy moc sygnału [math]x(t)[/math] (o skończonej energii) jak rozkład zmiennej losowej. Aby rozkład był unormowany trzeba podzielić go przez energię sygnału: [math]E_x = \int_{-\infty}^{\infty} |x(t)|^2 dt \lt \infty[/math]. Zatem rozkład ten jest postaci: [math]p(t) = \frac{1}{E_x}|x(t)|^2 [/math].

Jako lokalizację występowania sygnału w czasie przyjmujemy średnie położenie jego energii:

[math]t_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}t |x(t)|^2 dt[/math]

zaś jako miarę skupienia energii wokół tego położenia przyjmujemy wariancję:

[math]\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt [/math]

Analogicznie w dziedzinie częstości:

[math]f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df[/math]
[math]\sigma_f^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (f - f_0)^2 |X(f)|^2 df [/math]

Można pokazać (np. Pinsky, 2002), że iloczyn wariancji energii w czasie i w częstości jest ograniczony od dołu:

[math]\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}[/math]

Estymatory gęstości widmowej dla przestrzeni czas-częstość

Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak:

[math] E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}[/math]

i interpretujemy [math]|x(t)|^2[/math] albo [math]|X(f)|^2[/math] jako gęstości energii. Stąd pomysł, żeby rozszerzyć tą koncepcję na obie dziedziny jednocześnie i wprowadzić pojęcie gęstości energii w dziedzinie czas-częstość [math]\rho_x(t,f)[/math]:

[math] E_x=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{\rho_x(t,f) dt df}[/math]

muszą też być spełnione własności brzegowe:

[math] \int_{-\infty}^{\infty}{\rho_x(t,f) dt}=|X(f)|^2[/math]
[math] \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2[/math]

Dystrybucja energii

Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD):

[math] W_x(t,f)=\int_{-\infty}^{\infty}x(t+\tau/2)x^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]

lub

[math] W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi[/math]

Implementacja

Przykładowa implementacja WVD dla sygnału rzeczywistego:

"wersja w matlabie" 

function [Tfr,ts,f]=tf_wvd(x,Fs,varargin)

doplot = true;
switch nargin
    case 0:1
        disp('tf_wvd - not enough input arguments');
        return
    case 2

    otherwise
        doplot=varargin{1};
end

x = hilbert(x);
samples = length(x);
N = floor(samples/2);
t = 0:samples; t(end)= [];
tfr = zeros(N,samples);
for ti=t
    for tau=0:min(ti,samples-ti)-1
        tfr(tau+1,ti+1) = x(ti+tau+1).*conj(x(ti-tau+1));
    end
end

Tfr = fft(tfr,samples,1);
ts = t./Fs;
f = linspace(0,Fs/2,N);

if doplot
    pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;
end

Własności

Własności WVD:

  • zachowanie energii
  • własności brzegowe
  • zachowywanie przesunięcia w czasie i w częstości
[math] y(t) = x(t-t_0) \Rightarrow W_y(t,f) = W_x(t-t_0,f)[/math]
[math] y(t) = x(t)e^{i 2 \pi f_0 t} \Rightarrow W_y(t,f) = W_x(t,f-f_0)[/math]
  • zachowywanie skalowania
[math] y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)[/math]

Wyrazy mieszane

WVD jest reprezentacją kwadratową — dekompozycja sumy sygnałów nie jest sumą ich dekopozycji. Mamy więc:

[math] y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)[/math]

gdzie

[math] W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]

Rozdzielczość

  • idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej):

Wersja w Matlabie 

Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
ch = tf_chirp(5,Fs/2-5,T,Fs);
[Tfr,ts,f] = tf_wvd(ch,Fs,false);
subplot(2,1,1)
plot(t,ch)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;


  • struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności.

Wersja w Matlabie 

Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
s1 = tf_gabor(0.3, 0.05, 1.0, 100, 0, Fs);
s2 = tf_gabor(0.7, 0.05, 1.0, 200, 0, Fs);
s = s1 + s2;
[Tfr,ts,f] = tf_wvd(s,Fs,false);
subplot(2,1,1)
plot(t,s)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;


Klasa Cohena

WVD jest najprostszym elementem klasy Cohena. Ponieważ wyrazy mieszane mają wysoką częstość przestrzenną w płaszczyźnie czas-częstość to można je częściowo zniwelować poprzez zastosowanie odpowiedniego filtra. Koncepcja ta jest wykorzystywana w klasie Cohena. Ogólnie klasę tę można zapisać jako:

[math] C_x(t,f,\Pi) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \Pi(s-t, \xi - f) W_x(s,\xi) ds d\xi[/math]

gdzie

[math] \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df[/math]

Najczęściej [math] \Pi[/math] wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.

Krótkoczasowa transformacja Fouriera i spektrogram

Definicja krótkoczasowej transformacji Fouriera

Krótkoczasowa transformacja Fouriera (ang. short-time Fourier transform, STFT) może być rozumiana jako seria transformacji Fouriera wykonanych na sygnale podzielonym na okienka, przy czym położenie okienka w czasie jest w ramach takiej serii przesuwane monotonicznie. W wersji ciągłej możemy to zapisać tak:

[math]F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} [/math]

Własności

Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej:

[math] x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df [/math]

gdzie [math]E_h=\int_{-\infty}^{\infty}|h(t)|^2\,dt [/math] Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci:

[math]h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}[/math]

Każdy atom uzyskiwany jest przez translację pojedynczego okna [math]h[/math] w czasie i jego modulację częstością [math]f[/math].

Spektrogram

Definicja

Spektrogram: kwadrat modułu STFT jest estymatą gęstości energii w przestrzeni czas-częstość:

[math]S_x(t, f) =\left|\int_{-\infty}^{\infty}{x(u) h^*(u - t) e^{-i 2\pi f u} du}\right|^2[/math]

Implementacja

  • Spektrogram zaiplementowany jest w pythonie w module matplotlib.pyplot jako funkcja specgram (dokumentacja).
  • W matlabie spectrogram jest zaimplementowany w signal procesing toolbox:

dokumentacja

Własności

Przesunięcia

Spektrogram zachowuje przesunięcie:

w czasie

[math]y(t) = x(t - t_0)\Rightarrow S_y(t, f; h) = S_x(t - t_0, f; h)[/math]

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.1;
T     = 4.0;
f     = 10;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
 
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs); 
        % sygnał
sig2 = tf_gabor(t0 + 2, sigma, T, f, phi, Fs); 
        % sygnał przesunięty w czasie
 
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)), sig1, zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;

subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)), sig2, zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;

subplot(2,2,3)
time    = tf_czas(T, Fs);
plot(time,sig1);
  
subplot(2,2,4)
plot(time ,sig2);


i w częstości:

[math]y(t) = x(t) e ^{i 2 \pi f_0 t}\Rightarrow S_y(t, f; h) = S_x(t, f - f_0; h)[/math]

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.1;
T     = 4.0;
f     = 10;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
time    = tf_czas(T, Fs);
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs); 
        % sygnał
sig2 = tf_gabor(t0, sigma, T, f+20, phi, Fs);
        % sygnał przesunięty w częstości
 
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
 
subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
 
subplot(2,2,3)
plot(time,sig1);
 
subplot(2,2,4)
plot(time ,sig2);


Wyrazy mieszane

Spektrogram jest reprezentacją kwadratową. Spektrogram sumy sygnałów nie jest sumą spektrogramów sygnałów składowych, jest tam jeszcze coś:

[math]y(t) = x_1(t)+x_2(t) \Rightarrow S_y(t, f) = S_{x_1}(t, f)+S_{x_2}(t, f)+S_{x_1,x_2}(t, f)+S_{x_2,x_1}(t, f)[/math]

gdzie

[math]S_{x_1,x_2}(t, f) = F_{x_1}(t, f)F^*_{x_2}(t, f)[/math]

Jak mogą wyglądać wyrazy mieszane ilustruje poniższy kod. Kolejne subploty pokazują spektrogramy uzyskane dla sygnału będącego sumą dwóch funkcji Gabora o częstościach różniących się o 2 Hz i położeniach różniących się o kolejne wielokrotności 0,1 s.

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.05;
T     = 2.0;
f0    = 20;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
time  = tf_czas(T, Fs);
 
for i=0:8
    subplot(3,3,i+1)
    sig1  = tf_gabor(t0, sigma, T, f0, phi, Fs); % sygnal
    sig2  = tf_gabor(t0+i*0.1, sigma, T, f0+2, phi, Fs);
        % sygnał przesunięty w częstości o 2 Hz i w czasie o i*0.1 s
    sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
    sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
    P=spectrogram(sig1_padded+sig2_padded,NFFT,NFFT-1,NFFT,Fs);
    pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
end


Wyrazy mieszane występują także w przypadku pojedynczej struktury dla sygnału rzeczywistego. „Mieszające się” obiekty to energia zlokalizowana w dodatniej i ujemnej części widma częstości. Efekt jest stosunkowo słaby i uwidacznia się dopiero na mapach czas-częstość logarytmu gęstości energii. Problem ten można obejść stosując transformację Hilberta, gdyż po tej transformacji cała energia skupiona jest w dodatniej części widma. Własność tę ilustruje poniższy program:


Wersja w Matlabie 

% parametry
t0    = 0.5;
sigma = 0.1;
T     = 1.0;
f     = 30;
phi   = 0;
Fs    = 256.0;
NFFT  = 32;
Fs2   = floor(Fs/2);
 
s = tf_gabor(t0, sigma, T, f, phi, Fs);
t = tf_czas(T, Fs);
f = linspace(-Fs2,Fs2,NFFT+1); f(end) = [];
 
subplot(4,1,1)
plot(t,s);
 
subplot(4,1,2)
P=spectrogram(s,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),abs(P)); shading interp;
 
subplot(4,1,3)
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;
 
subplot(4,1,4)
s_ana = hilbert(s); % sygnał analityczny
P=spectrogram(s_ana,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;

Ćwiczenie:

  • Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek h.
  • Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych.


Ciągła transformata falkowa i skalogram

Ciągłą transformata falkowa

Definicja

Ciągła transformacja falkowa (ang. Continuous Wavelet Transform, CWT) dana jest wzorem:

[math] P_x(t,a;\Psi)= \int_{-\infty}^{\infty}{x(s)\Psi^*_{t,a}(s) ds}[/math]

gdzie

[math] \Psi_{t,a}(s) = \frac{1}{\sqrt{|a|}} \Psi\left(\frac{s-t}{a}\right)[/math]

a jest skalą. Od falki [math]\Psi[/math] wymagamy żeby miała średnią 0.

Transformację tę można interpretować jako rzutowanie sygnału na kolejne wersje falki [math]\Psi[/math] przesunięte o t i przeskalowane o a.

Inne spojrzenie na transformację falkową uwidacznia się gdy połączymy dwa powyższe wzory:

[math]P_x(t,a;\Psi)= \frac{1}{\sqrt{|a|}}\int_{-\infty}^{\infty}{x(s) \Psi^*\left(\frac{s-t}{a}\right) ds} [/math]

Tu widać, że dla ustalonej skali a transformacja falkowa jest splotem sygnału z falką o skali a. Ten sposób myślenia o transformacji falkowej umożliwia zastosowanie szybkiego algorytmu obliczeniowego bazującego na tym, że splot w dziedzinie czasu odpowiada mnożeniu w dziedzinie częstości.

Skalogram

Podobnie jak dla STFT i spektrogramu, możemy dla CWT wprowadzić pojęcie skalogramu, będącego estymatą gęstości energii w przestrzeni czas-skala.

[math]S_x(t,a;\Psi)=\left| P_x(t,a;\Psi)\right|^2[/math]

Dla falek, które są dobrze skupione wokół częstości [math]f_0[/math] dla skali [math]a_0=1[/math] można wprowadzić utożsamienie [math]f=\frac{f_0}{a}[/math]. Utożsamienie to pozwala przekształcić reprezentację czas-skala w reprezentację czas-częstość:

[math]S_x(t,f;\Psi)=\left| P_x(t,f_0/f;\Psi)\right|^2[/math]

Implementacja

Przykładowa implementacja obliczania skalogramu dla falek Morleta przedstawiona jest poniżej. Korzysta ona z własności splotu.

Wersja w Matlabie 

function [P,f,t]=tf_cwt(x,MinF,MaxF,Fs,varargin)

w = 7;
df = 1;
doplot = true;
switch nargin
    case 0:3
        disp('tf_cwt - not enough input arguments');
        return
    case 4

    case 5
        w=varargin{1};
    case 2
        w=varargin{1};
        df=varargin{2};
    otherwise
        w=varargin{1};
        df=varargin{2};
        doplot=varargin{3};
end

T = length(x)/Fs;
M = length(x);
t = 0:1/Fs:T; t(end) = [];
freqs = MinF:df:MaxF; freqs(end) = [];
P = zeros(length(freqs),M);
X = fft(x);

for i=1:length(freqs)
    f = freqs(i);
    s = T*f/(2*w);
    psi = fft(tf_morlet(M,w,s,true));
    psi = psi./sqrt(sum(abs(psi).^2));
    tmp = fftshift(ifft(X.*psi));
    P(i,:) = abs(tmp).^2;
end

if doplot
    pcolor(linspace(0,T,size(P,2)),linspace(MinF,MaxF,size(P,1)),P); shading interp;
end

MP — dopasowanie kroczące

Definicja

Dopasowanie kroczące (ang. matching pursuit, MP) jest procedurą polegającą na rozłożeniu sygnału [math]s(t)[/math] na funkcje składowe [math]g_{\gamma_n}[/math] pochodzące z określonego zbioru funkcji [math]D[/math] (tzw. słownika). Słowniki wykorzystywane w metodach czas-częstość często składają się z funkcji Gabora tj. funkcji sinus modulowanej funkcją Gaussa. MP jest algorytmem iteracyjnym. W pierwszym kroku wybierana jest funkcja dająca największy iloczyn skalarny z sygnałem. W każdym następnym kroku funkcja jest analogicznie dopasowywana do residuum sygnału, pozostałego po odjęciu wyniku poprzedniej iteracji.

Formalnie wygląda to następująco:

[math] \left \{ \begin{array}{l} R^0s = s\\ R^ns = \langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\ g_{\gamma_n} = \arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle| \end{array} \right . [/math]

gdzie: [math]\arg \max_{g_{\gamma_i} \in D }[/math] oznacza tego [math] g_{\gamma_i}[/math], który daje największy iloczyn skalarny z aktualnym residuum: [math]|\langle R^ns, g_{\gamma_i}\rangle|[/math].

Słowniki mogą być dowolne, ale najczęściej składamy je z funkcji Diraca, sinus i Gabora:

[math] g_\gamma (t) = K(\gamma)e^{ -\pi\left( \frac{t-u}{\sigma} \right)^2} \sin\left(2 \pi f (t-u)+\phi\right) [/math]

normalizacja [math] K(\gamma)[/math] jest taka, że [math] ||g_{\gamma}||=1[/math], [math]\gamma=\{ u, f, \sigma, \phi \}[/math] to parametry funkcji w słowniku ([math]u[/math] — translacja w czasie, [math] f[/math] — częstość, [math] \sigma[/math] — szerokość w czasie, [math] \phi[/math] — faza).

Dystrybucja energii

Reprezentację czas-częstość uzyskujemy z dekompozycji MP sumując dystrybucje WVD pojedynczych atomów:

[math] W_{ g_{\gamma_n}}(t, f)=\int g_{\gamma_n} \bigl (t + \frac{\tau}{2} \bigr)\; g_{\gamma_n}^*\left(t- \frac{\tau}{2} \right) e^{- i 2 \pi f \tau } d \tau [/math]
[math] E^{MP} = \sum_{n=0}^M |\langle R^n s, \;g_{\gamma_n} \rangle|^2 \; W_{g_{\gamma_n}} (t, f) [/math]

W wyrażeniu tym nie ma wyrazów mieszanych :-)



Implementacja MP, jest dostępna bezpośrednio w środowisku Matlab, jako plugin do EEGLAB. Program można pobrać ze strony [git.nimitz.pl/mp-eeglab-plugin.git/snapshot/18ad395338572078632297cd071ba5e925b7b22e.tar.gz], jednak wygodniejsze wydaje się bezpośrednie skopiowanie repozytorium. W tym celu należy:

Po ponownym uruchomieniu EEGLABa, MP będzie dostępne w zakładce tools. Wynik działania skryptu zapisywany jest do struktury BOOK. Przed wykonaniem kolejnych obliczeń, należy zapisać wyniki poprzednich. W przeciwnym razie zostaną one nadpisane. Do programu dołączone zostały stosowne narzędzia wizualizujące wyniki.

Ćwiczenia

Zadanie 1

  • Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod.
  • Zbadać własności metod czas-częstość, m.in.:
    • Proszę przyjrzeć się definicjom transformaty falkowej i STFT i opowiedzieć o analogiach i różnicach.
    • Proszę zbadać własności przesunięć w czasie i w częstości dla skalogramu w sposób analogiczny jak było to pokazane dla spektrogramu.
    • Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu.

Zadanie 2

Zbadaj działanie algorytmu MP na samodzielnie wytworzonych sygnałach symulowanych:

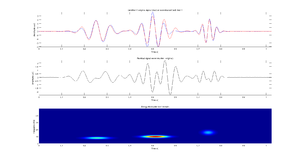
  • Trzech funkcjach Gabora o różnych częstościach, amplitudach i położeniach w czasie i o podobnej rozciągłości w czasie tak, aby zasadniczo nie nachodziły na siebie (patrz rysunek). Wykonaj dopasowanie dla trzech atomów, narysuj sygnał oryginalny i nałożony na niego sygnał zrekonstruowany z wyliczonych atomów, różnicę tych sygnałów (residuum) oraz mapę czas-częstość.
Eeglab gabory3.png
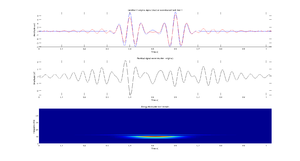
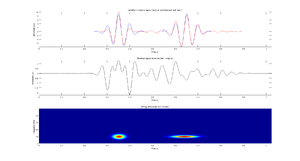
  • Dwóch jednakowych funkcji Gabora położonych w pewnej odległości od siebie w czasie. Zbadaj jakość dopasowania dokonując rekonstrukcji dwoma i trzema atomami na rysunkach podobnych jak w poprzedniej części zadania. Sprawdź co się dzieje przy zwiększaniu odległości w czasie pomiędzy tymi funkcjami Gabora.
Eeglab gabory2.png

Eeglab gabory2 dalej.png

Zadanie 3

Korzystając z danych SSVEP zebranych podczas zajęć w semestrze zimowym:

  • Uśrednić odcinki sygnałów zbierane dla tych samych częstości stymulacji, zostawiając przed i po sygnale okres referencyjny (np. 2 s).
  • Wykonać mapy czas-częstość za pomocą spektrogramu, korzystając z reprezentacji falek Morleta i Wignera-Villa.

Zadanie 4

Pobrać plik z danymi: http://www.fuw.edu.pl/~suffa/LabEEG/Characterize_ch4_F50_G4.mat

Opis danych: dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1 a 2 sekundą.

Analiza zapisów LFP z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca, o częstości 50 Hz. Mapa czas-częstość przedstawia względną gęstość energii (w skali dB) względem okresu referencyjnego 200-50 ms przed początkiem stymulacji. Dane opisane są w pracy: Supratim Ray, Steven S. Hsiao, Nathan E. Crone, Piotr J. Franaszczuk, and Ernst Niebur. Effect of Stimulus Intensity on the Spike—Local Field Potential Relationship in the Secondary Somatosensory Cortex. The Journal of Neuroscience, 2008, 28(29):7334-7343.

Zadania do wykonania:

  • Otrzymać mapy czas-częstość dla pojedynczych realizacji a następnie uśrednić je po realizacjach.
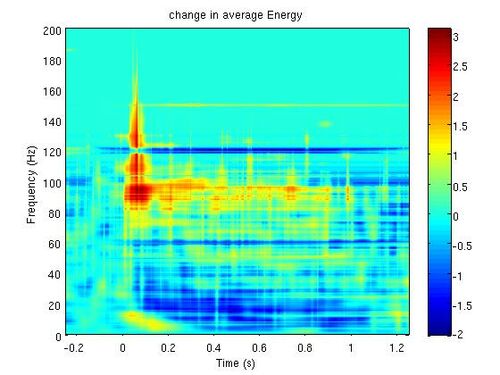
  • Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz).
  • W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje:
    • usunąć częstości sieci (60 Hz i wyższe harmoniczne);
    • zastosować logarytmiczną skalę energii;
    • policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym.

Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na rys. 1.

Zadanie 5

Wykonać analizę metodą MP dla danych z zadania 3.

Literatura

S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415.

Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6


Laboratorium_EEG/Czas-częstość

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Laboratorium_EEG/Analiza_czas-częstość_w_matlabie&oldid=4987”