Metody Biofizyki Molekularnej/Krystalografia białek

Strukturę przestrzenną białek złożonych maksymalnie z ok. 370 aminokwasów możemy uzyskać dzięki badaniom NMR. W przypadku większych białek stosuje się metody krystalograficzne. Odległości między obiektami i ich wielkości nie mogą być wyznaczane z rozdzielczością większą niż długość fali promieniowania za pomocą której oświetlamy układ. Aby uzyskać dane z rozdzielczością atomową potrzebne jest promieniowanie o odpowiednio krótkiej długości fali. Dlatego do określania struktury makromolekuł stosujemy promieniowanie rentgenowskie.

Historia

• W 1840 roku F.L. Hunefeld opisał przypadkowo powstałe kryształy hemoglobiny dżdżownicy.
• W 1912 roku Max von Laue przeprowadził pierwsze doświadczenie ugięcia promieniowania rentgenowskiego na krysztale. *Rok później William Henry Bragg i jego syn William Lawrence Bragg rozwiązali struktury kilku minerałów.
• W 1934 roku Arthur Lindo Patterson wyprowadził nazwaną od jego nazwiska funkcję Pattersona, która umożliwia rozwiązanie problemu fazowego dla struktur zawierających atom ciężkiego pierwiastka.
• Na początku lat 30. XX wieku pojawiły się pierwsze zdjęcia dyfrakcji: na włóknach białek w laboratorium Williama Astbury'ego i na monokryształach w laboratorium Desmonda Bernala.
• W 1951 roku Linus Pauling na podstawie obserwacji krystalograficznych i właściwości wiązań chemicznych zapostulował struktury alfa-helisy i beta-kartki, jako główne motywy w białkach (Nagroda Nobla 1954).
• Pod koniec lat 50. XX wieku John Kendrew opublikował pierwszą w dziejach strukturę białka, mioglobiny wieloryba. *W tym samym czasie Max Perutz opublikował strukturę hemoglobiny.
• W 1953 roku Rosalind Franklin zarejestrowała zdjęcia rentgenowskie włókien DNA.
• W 1965 roku uzyskano pierwszą strukturę lizozymu z białka jaja kurzego. W 1971 roku utworzono Bank Struktur Białkowych (Protein Data Bank, PDB), w którym zdeponowano 7 struktur białek. W roku 1973 w PDB było zdeponowanych 9 struktur białkowych.
• Powolny początkowo rozwój rentgenografii białek wynikał z braku silnych źródeł promieniowania rentgenowskiego. W latach 70-tych nastąpił skok jakościowy związany z zastosowaniem synchrotronów jako źródeł promieniowania rentgenowskiego, wprowadzeniem programowalnych maszyn cyfrowych, oraz rozwojem inżynierii genetycznej i biotechnologii.

Etapy uzyskiwania struktury białka

Do etapów uzyskiwania białka odpowiedniego do badań krystalograficznych, a następnie określania struktury krystalograficznej należą:

1. Oczyszczanie.
2. Krystalizacja (uzyskanie dobrze rozpraszającego monokryształu).
3. Wstępna analiza dyfrakcyjna (grupa przestrzenna, zdolność rozdzielcza, stabilność w wiązce).
4. Zebranie pełnych danych dyfrakcyjnych
5. Rozwiązanie problemu fazowego odpowiednią metodą:
   1. Podstawienia molekularnego
   2. Anomalnego rozpraszania
   3. Podstawienia izomorficznego pochodnych z ciężkimi atomami
6. Utworzenie mapy gęstości elektronowej
7. Interpretacja mapy, udokładnienie struktury
8. Prezentacja graficzna uzyskanej struktury białka

Czynniki wpływające na krystalizacje białek

Diagram fazowy

Na rozpuszczalność białek wpływają „czynniki wytrącające” (precypitanty): np.: sole, glikol polietylenowy. Diagram fazowy zależności stężenia białka od stężenia precypitanta jest przedstawiony na Rys. Figure 1.

Diagram fazowy dla hipotetycznego białka w funkcji stężenia precypitanta.
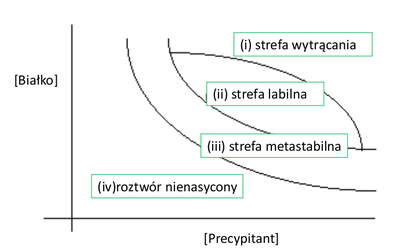
(i)Dla wysokich stężeń białka i precypitanta białko wytrąca się w postaci amorficznych agregatów.
(ii)Dla niższych stężeń mogą tworzyć się jądra krystalizacji, a następnie rozpraszające kryształy.
(iii)Dla jeszcze niższych stężeń, w strefie metastabilnej, nie tworzą się jądra krystalizacji, ale umieszczenie kryształu białka w takim roztworze powoduje jego wzrost.
(iv)Dla najniższych stężeń białka są całkowicie rozpuszczalne.

Jak w sposób kontrolowany przenieść białko do strefy przesycenia?

• Dodać precypitant.
• Suszyć kroplę cieczy zawierającej białko.
• Wymieniać bufor (dializa).
• Czekać i regularnie obserwować eksperyment pod mikroskopem.

Odparowywanie wody

Rozpuszczone białko umieszcza się w kropli (~5 ml) ponad lub obok rezerwuaru z buforem zawierającym większe stężenie czynnika wytrącającego. Kropla i rezerwuar ulegają równoważeniu wymieniając wodę. Osiągany zostaje stan przesycenia, tworzone są zarodzie krystalizacji i następuje wzrost kryształów.

Skład roztworu do krystalizacji (sól, bufor, precypitant) wpływa na rozpuszczalność białek.

• Ze zmiana pH niektóre aminokwasy (np. Asp, Glu, Lys, His, Arg, Try) zmieniają stan naładowania (z obojętnego na naładowany lub odwrotnie).
• Zawartość soli wpływa na ładunek powierzchniowy białka i oddziaływania z cząsteczkami wody. Wsalanie ( dodanie soli zwiększa rozpuszczalność białek) lub wysalanie (dodawanie soli zmniejsza rozpuszczalność białek)
• Rozpuszczalniki polarne np. Glikol polietylenowy (PEG) wiąże cząsteczki wody.

Optymalizacja środowiska krystalizacji

• Zakres krystalizacji białek to przedział 2 – 50 mg/ml .
• Przeprowadzenie testu PCT (Pre-crystallization test, Hampton Research) — pozwala na ustalenie granic stężenie białka zdolnego do krystalizacji pomiędzy precypitatem a przejrzysta kroplą.
• Temperatura i jej fluktuacje: białka zwykle krystalizują w zakresie temperatur 4 – 45°C, ale zdarzają się wyjątki np. glukagon (60°C). Najczęściej dwie równoległe hodowle w temperaturach 4°C i 20°C.
• Pożądana czystość (homogeniczność białka — chemiczna, izomeryczna, konformacyjna, oligomeryczna) testowana z wykorzystaniem m.in. elektroforezy natywnej (obserwuje się korelację pomiędzy heterogenicznością oligomeryczną białka a jego zdolnością do krystalizacji).

Inne czynniki, które wpływają na wzrost kryształów białkowych

• Dodatki — jony metali, ligandy,
• organizm, z którego wyizolowano białko,
• grawitacja, konwekcja, sedymentacja,
• drgania, dźwięki,
• objętość próbki,
• ciśnienie,
• proteoliza,
• lepkość roztworu,
• zanieczyszczenia,
• pole elektryczne i magnetyczne itp…

Należy szukać wielu możliwych warunków krystalizacji (w niektórych uzyskuje się małe kryształy, o kształcie igły, słabo rozpraszające promieniowanie rentgenowskie).

Jeśli nie uzyskamy w pierwszym podejściu kryształów odpowiednich do badań dyfrakcyjnych to należy zanotować obserwowane typy wytrąceń. Mogą to być wytrącenia amorficzne, nieamorficzne lub mikrokryształy. Doświadczony „badacz” może na podstawie typu wytrącenia zaplanować dalsze etapy postępowania w celu uzyskania kryształu.

Techniki uzyskiwania kryształów białek

1. Metoda wiszącej kropli.
   • Najbardziej rozpowszechniona technika.
   • Białko z roztworem zawierającym precypitant jest mieszane w stosunku 1:1.
   • Kropla umieszczana jest na silikonowanej płytce, którą zawiesza się nad zbiornikiem z roztworem.
   • Woda paruje z kropli do wyrównania stężeń precypitanta pomiędzy zbiornikiem a kroplą zawierającą białko.
   • Zwiększanie stężenia białka i precypitanta powoduje wzrost kryształów.
2. Metoda siedzącej kropli.
   • Technika podobna do „wiszącej kropli”.
   • Kropla umieszczana jest na silikonowanej płytce, którą umieszcza się na podstawce w zbiorniku z roztworem.
3. Dializa.
   • Roztwór białka jest oddzielony od roztworu zewnętrznego za pomocą półprzepuszczalnej membrany.
   • Wyrównywanie stężeń precypitanta pomiędzy rozdzielonymi membraną częściami naczynia powoduje wzrost kryształów.
4. Batch crystallization.
   • Krystalizator jest wypełniany roztworem nienasyconym.
   • Przesycenie jest osiągane przez stopniowe ochładzanie roztworu.
   • Kryształy o określonym rozkładzie rozmiarów uzyskuje się dzięki określonemu przebiegowi procesu zmiany temperatury w funkcji czasu.
5. Mikroposiew.
   • Pobranie kryształu z kropli.
   • Mycie kryształu.
   • Posiew w zrównoważonej kropli będącej w fazie metastabilnej.
   • Metoda stosowana dla białek, które krystalizują łatwo, ale mają tendencję do tworzenia małych kryształów.
6. Makroposiew.
   • Technika podobna do mikroposiewu.
   • Różnica — kryształ nie nadający się do badań dyfrakcyjnych jest kruszony.
   • Następnie pobierane są jego fragmenty i umieszczane w kropli będącej w fazie metastabilnej.

Kryształy białkowe

Kryształ to obiekt posiadający symetrię translacyjną.

Symetrie tworów skończonych to tzw. symetrie punktowe zachowujące przynajmniej jeden punkt w przestrzeni (figura przekształca się na siebie). Należą do nich:

• Obroty o kąt [math]\nicefrac{2\pi}n[/math], [math]n[/math] najczęściej równa się 2, 3, 4, lub 6.
• Inwersje względem punktu 0 — przekształcenie, w którym punkt P₁ przechodzi w punkt P₂, takie, że OP₁=-OP₂.
• Obroty inwersyjne — złożenie obrotu i inwersji względem punktu leżącego na osi obrotu. Odbicie zwierciadlane — złożenie obrotu dwukrotnego i inwersji.

Symetrie tworów nieskończonych (figura przekształca się na sąsiednią)

• translacje,
• obroty względem osi śrubowej (złożenie obrotu względem osi symetrii i translacji równoległej do tej osi),
• płaszczyzny ślizgowe (złożenie odbicia względem płaszczyzny symetrii i równoległej do niej translacji.

Białka zbudowane są wyłącznie z aminokwasów typu L ↠

• W wyniku operacji symetrii nie mogą utworzyć innego enancjomeru.
• Możliwe są tylko osie obrotu i osie śrubowe.

Opis struktury kryształu wymaga podania:

• Jednostki asymetrii — najmniejsza część kryształu, z której po zastosowaniu operacji symetrii (obroty, translacje, osie śrubowe) uzyskujemy komórkę elementarną, Jednostka asymetrii może zawierać jedną cząsteczkę aktywną biologicznie, część cząsteczki aktywnej biologicznie lub kilka cząsteczek aktywnych biologicznie.
  Przykład z PDB — struktura hemogloginy (aktywna biologicznie cząsteczka składa się z czterech łańcuchów:
  1. Struktura o ID 2hhb zawiera jedną cząsteczkę aktywnej biologicznie w jednostce asymetrii.
  2. Struktura o ID 1hho zawiera pół cząsteczki aktywnej biologicznie w jednostce asymetrii.
  3. Struktura o ID 1hv4 zawiera dwie cząsteczki aktywnej biologicznie w jednostce asymetrii.
• Komórki elementarnej — czyli najmniejszą powtarzającą się jednostkę w krysztale.
• Sieci Bravais’go — sieć, zgodnie z którą ustawione są elementy składowe w krysztale. Na podstawie symetrii sieci Bravais’go kryształy można podzielić na 7 układów krystalograficznych:
  1. układ trójskośny; P,
  2. układ jednoskośny; P, C,
  3. układ prostokątny (rombowy); P, C, F, I,
  4. układ tetragonalny; P, I,
  5. układ trygonalny; P,
  6. układ heksagonalny; P
  7. układ regularny; P, F, I,
  Gdzie oznaczenia P,C,F i I oznaczają położenia atomów: P oznacza atomy tylko w rogach komórki, I — dodatkowy atom w środku komórki, F — dodatkowy atom na każdej ścianie komórki, C — dodatkowy atom na wybranej ściance.

Fale

Równanie falowe jest najbardziej ogólną formą analitycznej reprezentacji ruchu falowego:

[math]\frac{\partial^2A(\vec r,t)}{\partial^2\vec r^2}=\frac1{v^2}\frac{\partial^2A(\vec r,t)}{\partial^2t}[/math].

Rozwiązanie równania falowego:

[math]A_n(\vec r,t)=A_0\cos(\vec k_n\cdot \vec r -\omega_nt+\phi_n)[/math].

Rozwiązanie ogólne równania falowego:

[math]A(\vec r,t)=\sum_nA_0e^{i\left(\vec k_n\vec r -\omega_n t +\phi_n\right)}[/math].

Zasada superpozycji: każde zaburzenie wywołane przez kilka fal emitowanych przez różne źródła można wyznaczyć dodając te fale i traktując je niezależnie od siebie.

Natężenie fali I jest wielkością rzeczywistą — mierzalną:

[math]I=|A(r,t)|^2\;[/math].

Prawo Braggów

Wzbudzone promieniowaniem protony i elektrony stają się źródłem promieniowania o częstości i długości fali promieniowania wzbudzającego. Mówimy wtedy o rozpraszaniu, którego szczególnym przypadkiem jest dyfrakcja czyli zjawisko rozpraszania w ściśle określonych kierunkach. Protony rozpraszają (1837)² razy słabiej niż elektrony.

Ilustracja prawa Braggów

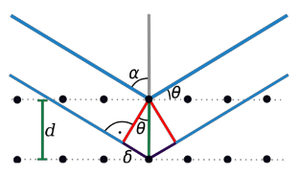
Prawo Braggów (Rys. Figure 2) (geometryczny warunek dyfrakcji promieni rentgenowskich na płaszczyznach krystalicznych o odległościach międzypłaszczyznowych [math]d_{hkl}\;[/math]):

[math]2\delta =2d_{hkl}\sin\theta = n\lambda\;[/math],

[math]\sin\theta = \frac{n\lambda}{2d_{hkl}}\leq 1\;[/math],

[math]\frac{n\lambda}2\leq d_{hkl}\;[/math],

gdzie: n — rząd odbicia lub ugięcia, [math]\theta\;[/math] — kąt odbicia wiązki promieni rentgenowskich od płaszczyzny sieciowej [math]hkl\;[/math].

Transformata Fouriera

Jeśli [math]F(k) = \int_{\vec r}f(r)e^{i\vec k\vec r}\mathrm dr[/math], to [math]F(k)\;[/math] jest transformatą Fouriera funkcji [math]f(r)\;[/math]. [math]f(r)\;[/math] można obliczyć następująco:

[math]f(r)=\int_{\vec k}F(k)e^{-i\vec k \vec r}\mathrm d k[/math].

Obie funkcje zawierają te same informacje, ale dotyczą różnych przestrzeni: rzeczywistej [math]f(r)\;[/math] i odwrotnej [math]F(k)\;[/math].

Splot funkcji

[math]c(u)=f(r)\star g(r)=\int_rf(r)g(u-r)dr\;[/math]

Ważne zależności

[math]T|f(\vec r)\star g(\vec r)|=|Tf(\vec r)|\cdot|Tg(\vec r)|[/math]

[math]T|f(\vec r)\cdot g(\vec r)|=|Tf(\vec r)|\star|Tg(\vec r)|[/math]

[math]Tc(\vec u)=T|l(\vec r)\star u(\vec r)|=|Tl(\vec r)|\cdot|Tu(\vec r)|[/math]

Dyfrakcja

Fale ulegające dyfrakcji na obiekcie zawierają informację o jego strukturze.

Rejestracja i analiza obrazu dyfrakcyjnego kryształu powinna doprowadzić do odtworzenia struktury kryształu.

Strukturę opisujemy za pomocą funkcji [math]f(r)\;[/math] — funkcja amplitudy obiektu, gdzie dla każdego punktu w krysztale możemy ustalić [math]r\;[/math].

Opis dyfrakcji zawiera informację o falach rozproszonych → zawiera funkcję charakterystyczna dla ruchu falowego.

Fala rozproszona przez element obiektu

[math]F(k)=\int_rf(r)e^{i(\vec k\vec r)}\mathrm dr[/math].

Obraz dyfrakcyjny

Obraz dyfrakcyjny dowolnego obiektu jest transformatą Fouriera jego funkcji amplitudy. Znając strukturę obiektu możemy obliczyć jego obraz dyfrakcyjny.

Zarejestrowawszy obraz dyfrakcyjny obiektu [math]F(k)\;[/math] możemy, dokonując odwrotnej transformacji Fouriera, obliczyć funkcję [math]f(r)\;[/math], czyli strukturę interesującego obiektu:

[math]F(k)=\int_rf(r)e^{-i(\vec k\vec r)}\mathrm dr[/math].

Problem: [math]F(k)\;[/math] — funkcja obrazu dyfrakcyjnego — jest funkcją zespoloną:

[math]F(k)=|F(k)|e^{i\phi}[/math]

Rejestrujemy tylko natężenie promieni ugiętych, czyli

[math]|F(k)|\;[/math].

Tracimy natomiast informację o czynniku fazowym [math]\phi\;[/math]. Jest to tzw. problem fazowy. Jego rozwiązanie jest niezbędne w celu obliczenia [math]f(r)\;[/math] i uzyskania struktury obiektu.

W jaki sposób informacja o strukturze obiektu zakodowana jest w jego obrazie dyfrakcyjnym?

Dyfrakcja na układzie szczelin

Rozważmy dwa typy siatek dyfrakcyjnych, jedna złożona z [math]n\;[/math] wąskich szczelin, druga z [math]n\;[/math] szerokich szczelin

1. Siatka dyfrakcyjna złożona z [math]n\;[/math] wąskich szczelin.
   1. Wraz ze wzrostem liczby szczelin główne maksima obrazu dyfrakcyjnego są coraz ostrzejsze.
   2. Wysokość wszystkich maksimów jest taka sama.
   3. Położenie maksimów dyfrakcyjnych jest stałe (odległość zależy od długości fali padającej i odległości pomiędzy szczelinami).
2. Siatka dyfrakcyjna złożona z [math]n\;[/math] szerokich szczelin — splot jednej szerokiej szczeliny i [math]n\;[/math] szczelin wąskich.
   1. Obrazem dyfrakcyjnym jest szereg maksimów o różnej wysokości równooddalonych.
   2. Wysokość tych maksimów nie zależy od liczby szczelin, mieści się w ramach obwiedni, która jest obrazem dyfrakcyjnym jednej szerokiej szczeliny.

Wnioski dla dwuwymiarowego układu szczelin przenoszą się na trójwymiarowy

Sieć przestrzenna kryształu może być reprezentowana przez trójwymiarową siatkę dyfrakcyjną.

Pozycje i sposoby rozmieszczenia w przestrzeni maksimów obrazu dyfrakcyjnego sieci przestrzennej kryształu zależą od odległości między węzłami sieci przestrzennej tego kryształu oraz od długości fali padającego nań promieniowania rentgenowskiego.

Natomiast dokonując pomiaru wysokości maksimów dyfrakcyjnych można odtworzyć kształt obwiedni obrazu dyfrakcyjnego motywu struktury. Dokonując jej transformacji oznaczymy strukturę motywu badanego kryształu.

Intensywność obrazu dyfrakcyjnego kryształu zawiera informacje o strukturze jego motywu — strukturze tworzących go molekuł.

Obraz dyfrakcyjny N szerokich szczelin:

Tf(N szczelin szerokich) = Tf(1 szczelina szeroka) * Tf(N szczelin wąskich)

Stąd:

Tf(struktury kryształu) = Tf(motywu) * Tf(sieci przestrzennej kryształu)

Dyfrakcja w sieci przestrzennej kryształu

Dla nieskończonej sieci przestrzennej:

[math]|F(\Delta \vec k)|=\sum_k\delta(\Delta \vec k\cdot \vec a -2h\pi)\cdot \sum_k\delta(\Delta \vec k\cdot \vec b -2k\pi)\cdot\sum_k\delta(\Delta \vec k\cdot \vec c -2l\pi)[/math].

Równanie jest iloczynem funkcji z których każda jest reprezentowana przez serię równoległych do siebie płaszczyzn.

Ze względu na właściwości delty Diraca funkcja jest różna od zera tylko w punktach przecięcia się wszystkich prostopadłych do siebie płaszczyzn.

Równanie opisuje zbiór węzłów sieci opisanej przez wektor ∆k czyli sieć odwrotną w przestrzeni Fouriera.

Sieć rzeczywista i odwrotna przekształcają się w siebie pod wpływem transformaty Fouriera. Obie są równoważnymi opisami budowy sieciowej kryształu.

Sieć odwrotną opisujemy wektorami bazy [math]a^*,\ b^*,\ c^*[/math]. Równanie jest spełnione, gdy są spełnione równania Laue’go.

[math]\Delta \vec k\cdot \vec a = 2\pi h[/math],

[math]\Delta \vec k\cdot \vec b = 2\pi k[/math],

[math]\Delta \vec k\cdot \vec c = 2\pi l[/math],

[math]H_{hkl} =ha^*+kb^*+lc^*\;[/math].

Wprowadzamy wektor, który wyznacza węzły sieci odwrotnej i odpowiada wartości [math]\Delta k\;[/math] dającej maksimum dyfrakcyjne

Zachodzi:

[math]a^* \bot b^*\ \mathrm i\ c^*[/math],

[math]b^* \bot a^*\ \mathrm i\ c^*[/math],

[math]c^* \bot b^*\ \mathrm i\ a^*[/math].

[math]H_{hkl}\;[/math] jest prostopadły do serii płaszczyzn [math]hkl\;[/math] w rzeczywistej sieci przestrzennej kryształu.

[math]|H_{hkl}|= \frac 1 {d_{hkl}}[/math], [math]d_{hkl}\;[/math] — rzeczywista odległość między płaszczyznami w rzeczywistej sieci przestrzennej kryształu.

[math]2d_{hkl}\sin\theta = n\lambda\;[/math]

Maksimum dyfrakcyjne występuje, gdy różnica dróg promieni odbitych jest równa całkowitej wielokrotności długości fali padającej.

Płaszczyzny [math]hkl\;[/math]

Okrąg (sfera) Ewalda

• Dla punktu P spełnione są równania Laue’go i Bragga.
• [math]\Delta k[/math] jest wektorem [math]H_{hkl}= h a^* + k b^* + l c^*\;[/math] sieci odwrotnej.
• Jeśli węzeł sieci odwrotnej znajdzie się na okregu Ewalda to zajdzie dyfrakcja — zarejestrujemy promień dyfrakcyjny (np. na błonie fotograficznej).
• W stanie statycznym na okręgu Ewalda dla danych warunków są trzy węzły sieci odwrotnej.

Liczba obserwowanych promieni ugiętych zwiększa się gdy obracamy kryształ. Rozszerzenie okręgu Ewalda do 3D — sfera Ewalda.

Plamki dyfrakcyjne na np. błonie światłoczułej są rzutem węzłów sieci odwrotnej, które odpowiadają maksimom dyfrakcyjnym i znalazły się na sferze odbicia podczas pomiaru. Plamki możemy wywskaźnikować przypisując im wskaźniki [math]hkl.\;[/math]

Położenia maksimów dyfrakcyjnych są zdeterminowane przez grupę przestrzenną (stałe sieciowe [math]a,\ b,\ c,\ \alpha,\ \beta,\ \gamma[/math]).

Natężenia maksimów są zdeterminowane rozłożeniami atomów w jednostce asymetrycznej.

Rozpraszanie na kryształach to rozpraszanie.

• Efektywnym źródłem promieniowania są elektrony.
• Obowiązuje zasada superpozycji: całkowita amplituda fali rozproszonej jest równa sumie amplitud fal pochodzących od każdego elektronu.
• Gęstość elektronowa ρ(r) może opisywać rozkład elektronów w komórce elementarnej kryształu – umożliwia lokalizację atomów i opis struktury.

Fala ugięta przez ciągły rozkład elektronów

Dla atomu:

[math]F(\delta k) =\int_{V_\mathrm{atomu}}f_e\rho(r)e^{i\Delta kr}\mathrm dr[/math]

Dla komórki elementarnej (KE) kryształu i stałej wartości [math]f_e\;[/math] (funkcja rozpraszania elektronu):

[math]F(\delta k) =\int_{V_\mathrm{KE}}f_e\rho(r)e^{i\Delta kr}\mathrm dr[/math]

[math]\Delta k =2\pi(ha^*+kb^*+lc^*)\;[/math],

[math]r=xa+yb+zc\;[/math],

[math]\Delta \vec k\cdot \vec r = 2\pi(hx+ky+lz)[/math],

[math]F(hkl)=\int_{\vec r}\rho(r)e^{2\pi i (hx+ky+lz)}[/math],

czynnik struktury (wielkość zespolona):

[math]F(hkl)=|F(hkl)|e^{i\phi}[/math],

[math]I(hkl)=[F(hkl)]^2[/math].

Znając rozkład gęstości ([math]\rho(r)\;[/math] możemy wyznaczyć [math]F(hkl)\;[/math], ale nie odwrotnie, tymczasem zależy nam na wyznaczeniu rozkładu gęstości przy znanym rozkładzie [math]F(hkl)\;[/math].

[math]\rho(\vec r) = \frac 1V \int_{\vec r} \vec F_{hkl}e^{-2\pi i (hx+ky_lz)}\mathrm d \Delta \vec k[/math].

Ze względu na rozkład dyskretny [math]F(hkl)\;[/math]:

[math]\rho(\vec r) = \frac 1V \sum_h\sum_k\sum_l \vec F_{hkl}e^{-2\pi i (hx+ky_lz)}[/math].

Sposoby rozwiązywania problemu fazowego:

1. Metody bezpośrednie
   1. Oparte na zależnościach pomiędzy pewnymi refleksami.
   2. Wymagana wysoka rozdzielczość i niewielkie układy.
   3. Popularna w przypadku badań niewielkich struktur.
2. Funkcja Pattersona.
3. Metoda podstawienia izomorficznego — wprowadzenie ciężkiego atomu do kryształu i obserwacja, które refleksy są z nim związane:
   1. wielokrotnego (Multiple Isomorfous Replacement, MIR),
   2. jednokrotnego, połączona z anomalnym rozpraszaniem (Multiple wavelength Anomalous Dispersion, MAD).
4. Metoda podstawienia molekularnego (Molecular Replacement, MR):
   1. znalezienie podobnej struktury i oparcie na niej pierwszych prób uzyskania rozwiązań,
   2. popularność wzrasta wraz z ilością rozwiązanych struktur.

Funkcja Pattersona

Atomy — obiekty punktowe — funkcja gęstości przyjmuje wartość [math]\rho_0[/math], gdy w położeniach [math]r\;[/math] i [math]r-u\;[/math] znajduje się atom, lub zero, w przeciwnym wypadku. Funkcja Pattersona jest równa wartości niezerowej, gdy wektor względnego położenia u jest równy odległości międzyatomowej. Obrazem funkcji [math]P(u)\;[/math] jest zbiór pików pojawiających się w miejscach odpowiadających odległościom między atomami.

Można wykazać, że:

[math]P(\vec u) = \frac 1V \sum_h\sum_k\sum_l |\vec F(hkl)|^2e^{-2\pi i (hx+ky_lz)}[/math]

Przykład: komórka elementarna jednowymiarowego kryształu złożona z trzech atomów w pozycjach [math]r = \{0; 0,2; 0,3\}\;[/math] — na widmie Pattersona piki w siedmiu pozycjach: [math]r'=\{-0,3; -0,2; -0,1; 0; 0,1; 0,2; 0,3\}\;[/math]. Jeśli [math]r=\{0; 0,1; 0,2\}\;[/math] na widmie Pattersona pięć pików [math]r'=\{-0,2; -0,1; 0; 0,1; 0,2\}\;[/math].

Odległość pomiędzy drugim i trzecim atomem jest równa odległości między pierwszym i drugim: 0,1. Oba te piki w tym samym miejscu, wysokości ich się zsumują, a rozdzielenie nie będzie możliwe.

Trudność w interpretacji mapy Pattersona wynikająca z ograniczeń pomiarowych widma dyfrakcyjnego. Pojedynczy pik jest złożony z piku centralnego i zbioru harmonicznych otaczających go. Zdarza się, że pierwsze harmoniczne (maksima poboczne) nakładają się na sąsiadujące piki. Maksima poboczne zniekształcają informację o położeniach atomów i utrudniają poprawne rozpoznanie pików Pattersona.

Informacje zawarte w mapie Pattersona są niejednoznaczne (trudności interpretacyjne)

Metoda wielokrotnego podstawienia izomorficznego

Polega na wprowadzaniu do kryształu bez wywoływania zmian w jego budowie sieciowej związków zawierających ciężkie atomy (Pt, Pb, Ag, Au, Hg) i uzyskaniu pochodnych izomorficznych, różniących się od kryształu niemodyfikowanego natężeniem niektórych promieni dyfrakcyjnych —co stwarza możliwość oznaczenia położeń atomów ciężkich w kryształach pochodnych izomorficznych a następnie znalezienia faz dla kryształu niezmodyfikowanego.

Rozpraszanie anomalne

Elektrony wewnętrznych powłok elektronowych nie mogą być traktowane jako swobodne oscylatory o częstości rezonansowej [math]\omega[/math] i współczynniku tłumienia [math]k\;[/math]. Czynnik rozpraszania dla elektronu:

[math]f=f_0+\Delta f'+\Delta f''\;[/math]

[math]\Delta f'\;[/math] — dyspersja,

[math]\Delta f''\;[/math] — absorpcja.

W 1925 roku Hermann Francis Mark wykazał, że rozpraszanie promieniowania rentgenowskiego w pobliżu progu absorpcji zależy od długości fali.

Dane dyfrakcyjne zabrane dla różnych częstości fali symulują izomorficzne podstawienia.

Metoda podstawienia molekularnego

Zastosowanie w rozwiązywaniu struktur białek blisko spokrewnionych z białkami o znanej strukturze i skatalogowanymi parametrami atomów. Znana cząsteczka jest modelem który służy do rozwiązywania struktury podobnej cząsteczki za pomocą funkcji translacyjnej i rotacyjnej.

[math]X_2 = CX_1+d\;[/math].

Zakładamy, że struktury są identyczne (pierwsze przybliżenie — ta sama gęstość elektronowa) i poszukujemy operatorów rotacji i translacji przeprowadzających jedną w drugą.

Poszukujemy minimum funkcji [math](F_\mathrm{obs}-F_\mathrm{calc})\;[/math] w dwóch etapach (translacja i rotacja).

Funkcja rotacji:

• Porównanie uzyskanej mapy Pattersona z mapą Pattersona wybranej struktury.
• Mapa Pattersona jest związana z orientacją molekuły, ale nie położeniem w komórce elementarnej.

Funkcja translacji:

• Mapa Pattersona jest bezużyteczna.
• Przesuwamy cząsteczkę w komórce elementarnej, liczymy teoretyczna wartość [math]F_{hkl}^\mathrm{calc}[/math] i porównujemy z obserwowana eksperymentalnie [math]F_{hkl}^\mathrm{obs}[/math].

Udokładnianie struktury

Udokładnianie struktury ma na celu zyskanie najlepszej zgodności pomiędzy modelem molekuły otrzymanym po rozwiązaniu problemu faz ze strukturą rzeczywistą w krysztale.

Dla białek różnice w niewielkim stopniu dotyczą łańcucha głównego, w znacznym reszt bocznych aminokwasów.

• Znając strukturę próbną ogląda się ją w programie graficznym i pozostawia tylko „dobre” atomy, mające sens fizyczny.
• Program SHELXL stosuje metodę najmniejszych kwadratów do polepszenia rozwiązania.
• Zmieniane są współrzędne atomów, tak aby obliczone z nich czynniki struktury |Fhkl|2 możliwie mało różniły się od obserwowanych.
• Po znalezieniu optymalnych współrzędnych atomów ze względu na dopasowanie do zbioru refleksów obliczana jest ponownie mapa gęstości elektronowej i porównywana z mapą otrzymaną na podstawie czynników struktury powstałych przez dodanie obliczonych faz do obserwowanego widma.
• W mapie różnicowej znajdujemy brakujące atomy i powtarzamy obliczenia aż do uzyskania zgodności obu map elektronowych (wynikającej z położenia atomów i obliczonej z czynników F).
• Na koniec krytycznie przyglądamy się jakości mapy i odpowiadamy na pytania:
  • Czy sekwencja zgadza się z gęstością elektronową i sekwencją pierwszorzędową?
  • Czy widać wszystkie ciężkie atomy ?
  • Czy kontakty w krysztale nie wprowadzają zaburzeń?
• Testem poprawności struktury są wykresy Ramachandrana podające zakres w jakim powinny mieścić się katy torsyjne wiązania peptydowego (kąt [math]\phi\;[/math] (fi) [math]\mathrm N - \mathrm C_\alpha\;[/math] i kąt [math]\xi\;[/math] (ksi) [math]\mathrm C_\alpha - \mathrm C\;[/math]) w zależności od drugorzędowej struktury białka.

Zbieranie danych dyfrakcyjnych

Dyfraktometr (urządzenie rejestrujące kierunki (kąty odbłysku) oraz natężenia ugiętych na krysztale wiązek promieniowania) składa się z:

• Źródła promieniowania.
• Monochromatora.
• Miejsca na próbkę.
• Detektora (licznik scyntylacyjny).
• Komputera sterującego dyfraktometrem i rejestrującego wyniki pomiarów.

Najczęściej stosowane metody

1. W metodzie Lauego na nieruchomy monokryształ pada wiązka równoległych promieni rentgenowskich o różnych częstościach. Zwykle stosuje się promieniowanie emitowane przez anodę wolframową, a średnica wiązki padającej wynosi 0,5-1,2 mm. Preparatem w tej metodzie jest na ogół monokryształ lub wycięta z niego płytka, o grubości 0,05-0,4 mm. Obraz dyfrakcyjny rejestruje się na płaskiej błonie fotograficznej ustawionej za kryształem, prostopadle do kierunku promieni pierwotnych.
2. W metodzie obracanego kryształu wiązka równoległa monochromatycznego promieniowania rentgenowskiego pada na niewielki monokryształ. Średnica lub szerokość wiązki wynosi od 0,5-1 mm. Badanemu kryształowi nadaje się najczęściej kształt walca o średnicy 0,1-0,3 mm i długości kilku milimetrów lub kulki o średnicy kilku dziesiątych milimetra. Przy takim kształcie preparatu, drogi jakie przebywają w krysztale wiązki ugięte promieniowania, należące do jednej warstwicy, są jednakowe. Ułatwia to określenie i porównanie ze sobą natężeń refleksów. Rentgenogramy wykonane tą metodą nazywa się dyfraktogramami warstwicowymi.
3. Metoda kołysanego kryształu jest odmianą metody obracanego kryształu. W metodzie kołysanego kryształu nie wykonuje on obrotu o pełne 360o, lecz jest obracany tam i z powrotem, w zakresie niewielkich kątów. Refleksów w warstwicach jest znacznie mniej niż w metodzie obracanego kryształu co pozwala uniknąć nakładania się ich na siebie. Ułatwia to wskaźnikowanie.
4. .Metoda Weissenberga — cylindrycznie zwinięta błona fotograficzna, umieszczona współosiowo z osią obrotu kryształu, przesuwa się — tam i z powrotem — równolegle do tej osi.

Źródła promieniowania

Promieniowanie rentgenowskie (promieniowanie w zakresie od 10 pm do 10 nm powstające w wyniku zderzeń elektronów z atomami) uzyskiwane jest poprzez wyhamowywanie rozpędzonych elektronów na materiale o dużej (powyżej 20) liczbie atomowej (promieniowanie hamowania) i wybijanie elektronów z atomów anody przez rozpędzone elektrony (promieniowania charakterystyczne anody) Źródłem promieniowania jest lampa rentgenowska. Położenie pasm w widmie charakterystycznym zależy od różnicy poziomów energetycznych, danego pierwiastka wykorzystanego przy konstrukcji lampy. Im wyższa liczba atomowa pierwiastka tym większe różnice energii między wewnętrznymi poziomami energetycznymi = emitowane promieniowanie o coraz krótszej fali.

Promień świetlny odbija się od powierzchni ściany kryształu, a promień rentgenowski, dzięki przenikalności w głąb, odbija się od wielkiej — w założeniu nieskończonej — liczby równoległych płaszczyzn sieciowych należących do tej samej rodziny [math](hkl)\;[/math]. Stąd wzmocnienie promieni odbitych od równoległych płaszczyzn następuje dla różnicy dróg będącej całkowitą wielokrotnością długości fali [math](n\lambda)\;[/math] (fale zgodne w fazie).

Promieniowanie synchrotronowe — efektywniejsze źródła promieniowania X — poruszające się po okręgu elektrony w synchrotronach. Duże natężenie promieniowania znacznie skraca czas uzyskiwania obrazów dyfrakcyjnych. Energia promieniowania emitowanego [math]\sim \frac{E^4}r\;[/math], gdzie: [math]E\;[/math] — energia elektronów, [math]r[/math] — promień krzywizny toru elektronów. Energie osiągane przez elektrony : 2-6 GeV.

Widmo promieniowania synchrotronowego ma charakter ciągły, ale można z niego wyciąć wiązkę monochromatyczną, którą wykorzystuje się w metodach dyfrakcyjnych. Natężenie promieniowania synchrotronowego jest 106-107 razy większe niż natężenie promieniowania pochodzącego z lamp rentgenowskich.