Uczenie maszynowe i sztuczne sieci neuronowe/Ćwiczenia 3

Zadanie: Filtr adaptywny

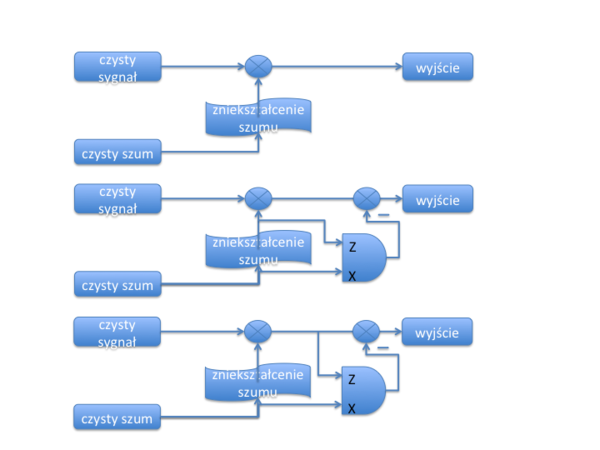
W tym zadaniu symulujemy działanie filtra, który może się adaptować do zmiennych warunków pracy. Jako przykład rozważymy redukcję szumu zniekształconego przez otoczenie. Załóżmy, że chcemy przekazywać głos pilota z kokpitu. Głos ten jest zniekształcony przez szum silników. W metodzie tej musimy mieć dwa mikrofony: jeden z nich rejestruje czysty odgłos silników, a drugi ten odgłos po przejściu drogi do okolic gdzie rejestrowany jest głos pilota. Można zastosować sieć neuronową do modelowania zniekształcenia szumu i ten zniekształcony szum odjąć od sygnału rejestrowanego przez mikrofon pilota.

Schemat

Przygotuj sygnały:

• częstość próbkowania niech będzie 100Hz
• czysty sygnał niech będzie reprezentowany przez sinusa o częstości 10Hz i trwający 2 s
• czysty szum niech będzie modelowany jako sygnał o tej samej długości co czysty sygnał, ale jego próbki to zmienne losowe z rozkładu normalnego
• szum zniekształcony niech będzie sumą osłabionego o 70% szumu i echa (sygnał opóźniony o jedną próbkę i amplitudzie zmniejszonej o 80%)
• sygnał zaburzony szumem to suma sinusa i szumu zniekształconego

Symulacja sieci

• Konstruujemy sieć liniową o dwóch wejściach i jednym wyjściu
• Przygotowujemy pusty zbiór uczący i przekazujemy go do obiektu typu BackpropTrainer, któremu przekazujemy sieć, ciąg uczący oraz parametry uczenia: współczynnik uczenia i bezwładność.
• Główna pętla symulacji iteruje się po kolejnych próbkach czasu:
  1. Do bufora pobieramy wycinek czystego szumu z chwili bieżącej i tylu poprzednich jaki jest rozmiar wejścia.
  2. Nadpisujemy zbiór uczący próbką zawierającą bieżący bufor i aktualną wartość zniekształconego szumu.
  3. Uczymy sieć na tym jedno-przykładowym zbiorze uczącym.
  4. Obliczamy sygnał jaki sieć zwróciłaby dla aktualnego bufora.
  5. Jako "oczyszczony sygnał" traktujemy różnicę między sygnałem zaburzonym i aktualnym wyjściem sieci.
  6. Zbieramy we wcześniej przygotowanych tablicach:
     • aktualne wagi sieci
     • kolejno otrzymane próbki "oczyszczonego sygnału"

Wykresy

Na subplotach przedstaw:

• sygnał czysty na tle sygnału zaburzonego
• ewolucję wag
• sygnał oczyszczony na tle sygnału zaburzonego

Szkielet rozwiązania:

# -*- coding: utf-8 -*-
# demostracja redukcji szumu znieksztalconego przez otoczenie


import numpy as np
import pylab as py

# przygotowujemy dane wejsciowe
Fs = 100.   # częstość próbkowania niech będzie 100Hz
dt = 1/Fs
f = 10.
# 2 sek. wektor czasu
t=np.arange(0,2,dt)
# to jest czysty sygnal: csinus o częstości 10Hz i trwający 2 s

sygnal= ...
# to jest oryginalny szum: czysty szum niech będzie modelowany jako sygnał o tej samej długości co czysty sygnał, ale jego próbki to zmienne losowe z rozkładu normalnego
szum = ...

# ciag wzorcow: na wejscie podajemy czysta postac szumu
X = szum
# szum ten jest modyfikowany na drodze od swojego zrodla do mikrofonu
# np zmniejsza sie jego amplituda do 30%
Z = 0.3*X
# i dodaje sie echo z amplitudą 20%
Z[2:] = Z[2:] + 0.2*X[1:-1];
# zmodyfikowany szum (obcinamy efekty brzegowe)
Z = Z[2:-1];
t=t[2:-1];
sygnal = sygnal[2:-1]
X = X[2:-1]
# do mikrofonu efektywnie trafia sygnal i znieksztalcony szum
zaszum_sygnal = sygnal + Z   #0.3*szum;

# narysuj na 3 subplotach:
# - czysty sygnał
# - czysty szum
# - to co trafia do mikrofonu

# tu zaczynamy rysunek, który będzdie obrazował c dzieje się w trakcie symulacji
py.figure(1)
py.subplot(3,1,1)
py.plot(t,sygnal,t,zaszum_sygnal)
py.title('stan poczatkowy')

# pomysl zastosowania tu sieci polega na tym, aby sieć modelowala to co
# dzieje sie z szumem na drodze od zrodla do mikrofonu:
# zmodyfikowany_szum = F(szum).
# Znajac czysty szum,
# odwzorowanie modyfikujace szum i zaszumiony sygnal mozemy odtworzyc
# czysty sygnal
# sygnal = zaszum_sygnal - F(szum)

# importujemy moduły do konstrukcji sieci
from pybrain.structure import FeedForwardNetwork, LinearLayer, FullConnection
from pybrain.supervised.trainers import BackpropTrainer
from pybrain.datasets import SupervisedDataSet

#Konstruujemy sieć liniową o dwóch wejściach i jednym wyjściu
# wytwarzamy pustą sieć
siec = ...
# tworzymy węzły wejściowe i wyjściowe
N_wej = ...
warstwaWejsciowa = ...
warstwaWyjsciowa = ...
# dodajemy węzły do sieci
# warstwy wejściowej
...(warstwaWejsciowa)
# warstwy wyjściowej
...(warstwaWyjsciowa)
# łączymy węzły
wej_do_wyj = ...
siec.addConnection(...)
# inicjujemy strukturę sieci
siec. ...

#Przygotowujemy pusty zbiór uczący
CU = SupervisedDataSet(...)
# przekazujemy go do obiektu typu BackpropTrainer
trainer = BackpropTrainer(...,...,learningrate=0.01, momentum=0.9,verbose = True)
# przygotowujemy tablice na zbieranie historii wag
w = np.zeros((len(t),N_wej) )
b = np.zeros(len(t))
# i na poprawiony sygnal oraz wyjście sieci
syg_poprawiony = np.zeros(len(t))
wyj = np.zeros(len(t))

# Główna pętla symulacji iteruje się po kolejnych próbkach czasu
for i in range(N_wej,len(t)):
    # Do bufora pobieramy wycinek czystego szumu z chwili bieżącej
    bufor_wyjściowy = ... #aktualną wartość zniekształconego szumu [i]
    bufor_wejsciowy = ...# wycinek czystego szumu z chwili bieżącej i tylu poprzednich jaki jest rozmiar wejścia i to odwrócony w czasie [i:i-N_wej:-1]
    # Nadpisujemy zbiór uczący próbką zawierającą bieżący bufor i aktualną wartość zniekształconego szumu
    CU = SupervisedDataSet(N_wej, 1)    
    CU.addSample(...)
    #Uczymy sieć na tym jedno-przykładowym zbiorze uczącym 
    trainer.trainOnDataset(CU)
    # zapamiętujemy parametry w tablicy 
    w[i,...] = ...
    # Obliczamy sygnał jaki sieć zwróciłaby dla aktualnego bufora:
    wyj[i] = ...
    #Jako "oczyszczony sygnał" traktujemy różnicę między sygnałem zaburzonym i aktualnym wyjściem sieci.
    syg_poprawiony[i] = ... 

py.subplot(3,1,2)
py.plot(w) # rysujemy ewolucję wag
py.title('wagi')
py.subplot(3,1,3)
py.plot(syg_poprawiony,'r') # sygnał oczyszczony na tle sygnału zaburzonego
py.plot(zaszum_sygnal,'g') 

py.show()

Pytania

• Czy jest związek między stanem wag i oczyszczaniem sygnału? O czym on świadczy?
• Dodaj do symulacji zmianę zaburzenia sygnału, np. w połowie symulacji niech dwukrotnie wzrośnie udział echa. Czy układ podąża za zmianą ?
• Spróbuj w punkcie 2 głównej pętli zamienić pożądaną wartość z aktualnej wartości zniekształconego szumu na aktualną wartość sygnału zaburzonego. Czy sieć nadal jest w stanie odfiltrować zaburzenia? Jeśli tak to dlaczego?