FizykaI FMiN/Zasada Zachowania Pedu

Zasada zachowania pędu

Zasada zachowania pędu

Układ izolowany

Układem izolowanym nazwiemy układ, w którym każde ciało może w dowolny sposób oddziaływać z innymi elementami układu, ale brak jest oddziaływań ze światem zewnętrznym.

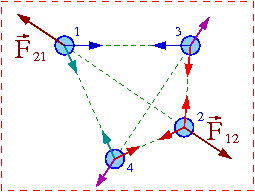
Z III zasady dynamiki siły z którymi działają na siebie ciała [math]i[/math] i [math]j[/math] związane są relacją:

[math] \vec{F}_{ij} \; = \; -\vec{F}_{ji} [/math]

Suma sił działających ciało [math]i[/math]:

[math] \vec{F}^{\Sigma}_{i} \; = \; \sum_j \vec{F}_{ji} [/math]

Suma sił działających na cały układ:

[math] \vec{F}_{tot} \; = \; \sum_i \vec{F}^{\Sigma}_{i} \; = \; \sum_i \sum_j \vec{F}_{ji} [/math]

[math] \; = \; \sum_j \sum_i - \vec{F}_{ij} \; = \; - \vec{F}_{tot} [/math]

Wynika z tąd, że całkowita siła działająca na układ izolowany

[math] \vec{F}_{tot} = 0 [/math]

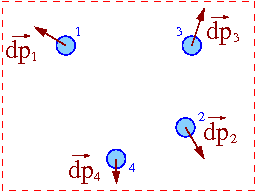
Korzystając z II zasady dynamiki możemy powiązać zmiany pędu każdego ciała układu z sumą działających na nie sił:

[math]\frac{d\vec{p}_i}{dt} \; = \; \vec{F}^{\Sigma}_{i} [/math]

Prawo ruchu dla całego układu:

[math] \vec{F}_{tot} \; = \; \sum_i \vec{F}^{\Sigma}_{i} = \sum_i \frac{d\vec{p}_i}{dt} [/math]

[math] \; \; = \; \frac{d}{dt} \sum_i \vec{p}_i [/math]

Skoro dla układu izolowanego całkowita siła znika to wektor całkowitego pędu musi pozostawać stały

[math] \vec{F}_{tot}=0 \;\;\; \Rightarrow \;\;\; \sum_i \vec{p}_i = \vec{p}_{\Sigma} = const [/math]

Dla dowolnego układu izolowanego, suma pędów wszystkich elementów układu pozostaje stała (zakładamy, że jest to izolowany układ inercjalny).

Oddziaływanie dwóch ciał

Przed "rozpadem"

Po "rozpadzie", [math] M_1 \; \lt M_2 [/math]

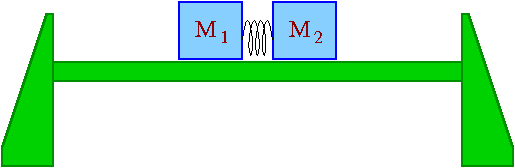
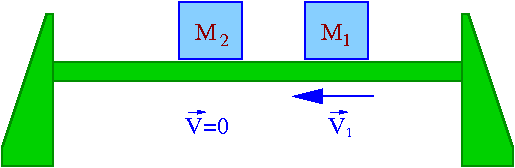
Układ dwóch ciał o masach [math] m_1[/math] i [math]m_2[/math] (w pokazie były to wózki na torze powietrznym: rysunek obok) "rozpada się" pod wpływem sił wewnętrznych.

Jeśli na początku wszystkie obiekty spoczywają

[math]\sum_i \vec{p}_i \; = \; 0 [/math]

to i po "rozpadzie" suma pędów musi być równa 0.

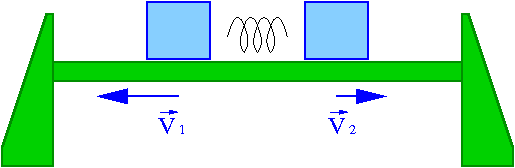
Dla dwóch ciał (przyjmując, że prędkości [math]v_i \ll c[/math])

[math] m_1 \vec{v}_1 + m_2 \vec{v}_2 \; = \; 0 [/math]

Co prowadzi do związku:

[math] \vec{v}_2 \; = \; - \frac{m_1}{m_2} \cdot \vec{v}_1 [/math]

[math] \frac{v_2}{v_1} \; = \; \frac{m_1}{m_2} [/math]

Zderzenie całkowicie niesprężyste

Przed zdrzeniem

Po zderzeniu

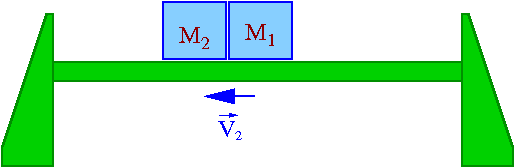
Zderzeniem całkowicie niesprężystym nazywamy zderzenie, w wyniku którego po zderzeniu ciała pozostają trwale złączone (poruszają się jak jedno ciało). W naszym doświadczeniu zczepiają się dwa wózki na torze powietrznym.

Przyjmijmy, że jedno ciało na początku spoczywa, a drugie uderza w nie z zadaną prędkością początkową (patrz rysunek obok).

Pęd początkowy:

[math] \vec{p}_i \; = \; m_1 \vec{v}_1 [/math]

Pęd końcowy:

[math] \vec{p}_f \; = \; (m_1 + m_2) \cdot \vec{v}_2 [/math]

Zasada zachowania pędu stanowi, że pęd nie może ulec zmianie (działają tylko siły wewnętrzne, między ciałami):

[math] \vec{p}_i \; = \; \vec{p}_f [/math]

Możemy z tego wyznaczyć prędkość ciał po zderzeniu:

[math] \vec{v}_2 \; = \; \frac{m_1}{m_1 + m_2}\cdot \vec{v}_1 [/math]

Ruch ciał o zmiennej masie

Rozważmy ruch ciała o zmiennej masie. Może to być rakieta, której masa w wyniku spalania paliwa (i wyrzucania gazów przez dysze silników rakietowych maleje). W ogólnym przypadku masa może zależeć od położenia, prędkości i czasu: [math]m = m(\vec{r},\vec{v},t)[/math]

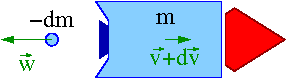
Rozważmy ruch rakiety. Przyjmijmy, że w jakiejś chwili czasu od ciała o masie [math]m-dm[/math] poruszającego się z prędkością [math]\vec{v}[/math] odłącza się element [math]-dm\gt 0[/math] poruszający się z prędkością [math]\vec{w}[/math]. Przyjmujemy, że [math]dm\lt 0[/math] ponieważ masa rakiety maleje.

Z zasady zachowania pędu:

[math] (m-dm)\; \vec{v} \; = \; m\; (\vec{v}+ d\vec{v}) - dm \; \vec{w} [/math]

Z czego możemy wyznaczyć zmianę pędu rakiety:

[math] d\vec{p} \; = \; m \; d\vec{v} \; = \; (m-dm)\; \vec{v} - m\; \vec{v} + dm \; \vec{w} [/math]

[math] \; = \; dm \; (\vec{w} - \vec{v}) \equiv dm \; \vec{v}_{odrz} [/math]

Działającą na rakietę siłę odrzutu (siła ciągu rakiety) możemy wyznaczyć z II zasady dynamiki:

[math] \vec{F}_{odrz} \; = \; \frac{d\vec{p}}{dt} \; = \; \frac{dm}{dt}\; \vec{v}_{odrz}[/math]

Przy czym siła ta jest przeciwnie skierowana do kierunku wylotu gazów ([math] \vec{v}_{odrz}[/math]), gdyż masa rakiety maleje ([math]\frac{dm}{dt}\lt 0 [/math])

Wzór Ciołkowskiego

Równanie ruch ciała pod wpływem siły odrzutu możemy więc zapisać w postaci:

[math] \frac{d \vec{p}}{dt} \; = \; m \; \frac{d \vec{v}}{dt} \; = \; \vec{F}_{zewn} \; + \; \frac{dm}{dt}\; \vec{v}_{odrz} [/math]

Zaniedbując wpływ sił zewnętrznych (np. pola grawitacyjnego) mamy:

[math] m \; \frac{d \vec{v}}{dt} \; = \; \frac{dm}{dt}\; \vec{v}_{odrz} [/math]

Wprowadzając funkcję [math]\vec{v}(m)[/math] określającą zależność prędkości od masy rakiety i korzystając ze wzoru na pochodną funkcji złożonej:

[math] m \; \frac{d \vec{v}}{dm}\cdot \frac{dm}{dt} \; = \; \frac{dm}{dt} \; \vec{v}_{odrz} [/math]

Otrzymujemy:

[math] m \; \frac{d \vec{v}}{dm} \; = \; \vec{v}_{odrz} [/math]

Całkując stronami:

[math] \int\limits_{v_\circ}^{v_k} \frac{d\vec{v}}{\vec{v}_{odrz}} \; = \; \int\limits_{m_\circ}^{m_k} \frac{dm}{m} [/math]

[math] \vec{v}_k \; = \; \vec{v}_\circ + \vec{v}_{odrz} \cdot \ln \left(\frac{m_k}{m_\circ} \right) [/math]

Otrzymaliśmy wzór Ciołkowskiego uzależniający prędkość końcową rakiety od zmiany masy.

Rakieta jednostopniowa

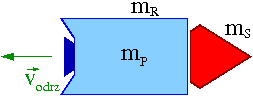
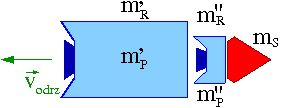
Przyjmijmy, że rakieta o masie [math]m_R[/math] ma wynieść satelitę o masie [math]m_S[/math], zużywając paliwo o masie [math]m_P[/math].

Możliwa do uzyskania prędkość końcowa:

[math]v_k \; = \; v_{odrz} \cdot \ln \left(\frac{m_S + m_R + m_P}{m_S + m_R} \right) [/math]

[math] \; \approx \; v_{odrz} \cdot \ln (1+f) [/math]

gdzie [math] f \; = \; \frac{m_P}{ m_R} [/math] to stosunek masy paliwa do masy rakiety. Zaniedbaliśmy przy tym masę satelity (nowoczesna elektronika jest lekka): [math] m_s \ll m_R [/math].

Aby uzyskać II prędkość kosmiczną [math]v_k \approx 11 \; km/s[/math] (np. lot na Księżyc) przy silniku rakietowym o [math]v_\circ = 3 \; km/s[/math] potrzebujemy:

[math] f \; = \; \exp \left( \frac{v_k}{v_\circ} \right) - 1 \; \approx \; 38 [/math]

Jest to teoretycznie możliwe do uzyskania, praktycznie jednak niewykonalne (?) i nieopłacalne !...

W praktyce budujemy rakiety wielostopniowe.

Rakieta dwustopniowa

Rakietę dzielimy na dwa człony o masach [math]m'_R[/math] i [math]m''_R[/math], w których znajduje się paliwo o masie [math]m'_P[/math] i [math]m''_P[/math]. Całkowite masy rakiety i paliwa:

[math]m'_R + m''_R = m_R[/math]

[math]m'_P + m''_P = m_P[/math]

Prędkość końcową liczymy stosując dwukrotnie wzór Ciołkowskiego (najpierw dla pierwszego, potem dla drugiego członu rakiety):

[math]v_k \; = \; v_{odrz} \cdot \left[ \ln \left(\frac{m_S + m_R + m_P}{m_S + m_R + m''_P} \right) + \ln \left(\frac{m_S + m''_R + m''_P}{m_S + m''_R} \right) \right][/math]

W przybliżeniu [math]m_S \ll m''_R \ll m'_R[/math] (pierwszy człon dużo większy od drugiego) i [math]m''_P \ll m'_P[/math] prowadzi to do zależności:

[math]v_k \approx v_{odrz} \cdot 2 \; \ln (1+f)[/math]

Aby uzyskać II prędkość kosmiczną [math]v_k \approx 11 \; km/s[/math] przy [math]v_\circ = 3 \; km/s[/math] potrzebujemy silnika rakietowego o współczynniku:

[math] f \; = \; \exp \left( \frac{v_k}{2 \; v_\circ} \right) - 1 \; \approx \; 5.3 [/math]

Dla [math]f \approx 10[/math] (dla obu członów) można wystrzelić w kosmos [math]m_S \approx 0.6% \; (m_R+m_P)[/math] (przy optymalnym wyborze [math]m''_R \approx 7% \; m_R[/math]).

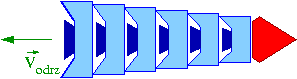
Rakieta wielostopniowa

Rakieta składa się z wielu członów. W każdym z nich stosunek masy paliwa do "obudowy" wynosi [math]f[/math]

W granicy wielu bardzo małych członów:

[math] m \; d\vec{v} \; = \; dm \; \vec{v}_{odrz} \cdot \frac{f}{f+1} [/math]

Co po odcałkowaniu sprowadza się do wzoru na prędkość końcową:

[math]v_k \; = \; v_{odrz} \cdot \frac{f}{f+1} \cdot \ln \left(\frac{ m_R + m_P + m_S}{m_S} \right) [/math]

[math] \; = \; v_{odrz} \cdot \frac{f}{f+1} \cdot \ln \left(1 +\frac{ m_R}{m_S} (1 + f) \right) [/math]

Aby uzyskać II prędkość kosmiczną dla satelity o masie [math]m_S \approx 100 \; kg[/math] przy silniku o [math]f=10[/math] musimy zbudować rakietę o masie

[math] m_R \; = \; \frac{m_S}{1+f} \left[ \cdot \exp \left( \frac{v_k \; (1+f)}{v_\circ \; f} \right) -1 \right] [/math]

[math] m_R \; \approx \; 500 \; kg [/math]

[math] m_P \; \approx \; 5000 \; kg [/math]

Przy rakiecie jednoczłonowej, przy tych samych [math]m_S[/math] i [math]m_R[/math] potrzebaby 228'000 kg paliwa !!!

Dla rakiety dwuczłonowej potrzebaby [math]m_R \approx[/math] 1600 kg, [math]m_P \approx[/math] 16'000 kg

Zasada zachowania momentu pędu

Siły centralne

Jeśli układ ciał (lub pojedyńcze ciało) działa jakaś siła zewnętrzna [math] \vec{F}_{tot} \ne 0[/math] to pęd układu musi się zmieniać:

[math]\sum \vec{p}_i \ne[/math] const.

Siły które działają na układ często są siłami centralnymi - działają w kierunku ustalonego źródła siły.

Jeśli położenie źródła przyjmiemy za środek układu współrzędnych to możemy wtedy zapisać:

[math] \vec{F}_{tot} = F(r, \ldots ) \cdot \vec{i}_r[/math]

Przykład:

• siła grawitacyjna [math]F(r) = -G\frac{m_1 m_2}{r^2} [/math]

• siła kulombowska [math]F(r) = \frac{Q_1 Q_2}{4 \pi \epsilon_\circ r^2} [/math]

• siła spężysta [math]F(r) = -k \cdot r [/math]

Czy można coś "uratować" z zasady zachowania pędu ?...

Moment pędu

Zdefiniujmy dla punktu materialnego możemy zdefiniować moment pędu względem O

[math] \vec{L} \; = \; \vec{r} \times \vec{p}[/math]

Moment pędu zależy od wyboru początku układu!

Uwzględniając klasyczne wyrażenie na pęd ([math]v \ll c[/math]) otrzymujemy:

[math] \vec{L} \; = \; m \; \vec{r} \times \vec{v} [/math]

Wartość momentu pędu: [math] L \; = \; m \; r \; v \sin \theta [/math] gdzie [math] \theta [/math] jest kątem między wektorem prędkości i wektorem położenia.

W przypadku ruchu po płaszczyźnie przechodzącej przez początek układu

[math] \vec{L} \; = \; m \; \vec{r} \times (\vec{v}_r + \vec{v}_\theta) [/math]

Wektor prędkości radialnej jest równoległy do wektora położenia więc ich iloczyn wektorowy znika. Wektor momentu pędu będzie prostopadły do płaszczyzny ruchu a jego wartość

[math] L \; = \; m \; r \; v_\theta \; = \; m \; r^2 \; \frac{d\theta}{dt} \; = \; m \; r^2 \; \omega [/math]

gdzie kąt [math]\theta[/math] opisuje położenie ciała w płaszczyźnie ruchu.

Przypadkiem szczególnym jest ruch po okręgu, czyli [math]r[/math]=const

Wtedy możemy zdefiniować Moment bezwładności

[math] I \; = \; m \; r^2 [/math]

a moment pędu możemy przedstawić w ogólnej postaci

[math] \vec{L} \; = \; I \; \vec{\omega} [/math]

Moment siły

Jeśli na ciało działa siła to możemy zdefiniować jej moment względem początku układu O

[math] \vec{M} \; = \; \vec{r} \times \vec{F}[/math]

Rozważmy zmiany momentu pędu w czasie:

[math] \frac{d\vec{L}}{dt} \; = \; \frac{d(\vec{r} \times \vec{p})}{dt} [/math]

[math] = \; \frac{d\vec{r}}{dt} \times \vec{p} \; + \; \vec{r} \times \frac{d\vec{p}}{dt} [/math]

[math] = \; \vec{v} \times \vec{p} \; + \; \vec{r} \times \vec{F} [/math]

[math] \; = \; 0 \quad +\quad \vec{M} [/math]

Otrzymaliśmy równanie ruchu, które mówi nam, że zmiana momentu pędu musi być wynikiem działania momentu siły:

[math] \frac{d\vec{L}}{dt} \; = \; \vec{M} [/math]

W przypadku, gdy na układ nie działają zewnętrzne momenty siły całkowity moment pędu jest zachowany:

[math] \vec{M}=0 \; \Rightarrow \; \vec{L}=const [/math]

Cząstka swobodna

Dla cząstki swobodnej moment pędu względem dowolnego punktu 0 pozostaje stały:

[math] L \; = \; m\; v\; r\; \sin \theta \; = \; m \; v \; b \; = \; \textrm{const} [/math]

gdzie [math] \theta [/math] jest (jak poprzednio) kątem między wektorem prędkości i wektorem położenia, zaś [math]b=r\; \sin \theta[/math] nazywamy parametrem zderzenia. Jest to odległość najmniejszego zbliżenia ciała do O.

Siła centralna

Dla dowolnej siły centralnej, moment siły (względem źródła):

[math] \vec{M} \; = \; \vec{r} \times \vec{F} [/math]

[math] = \; \vec{r} \times \vec{i}_r \cdot F(r,\ldots) \; = \; 0 [/math]

Moment siły znika, tak więc moment pędu, liczony względem źródła siły centralnej pozostaje stały.

[math]\vec{L}[/math] = const

Prędkość polowa

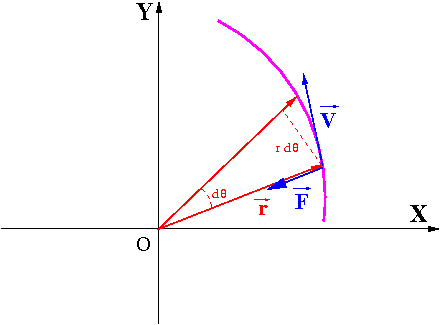
Prędkość polowa mówi nam jakie pole wektor wodzący punktu zakreśla w jednostce czasu ([math]\frac{dS}{dt}[/math])

Korzystając ze wzoru na pole trójkąta i przybliżenia małych kątów:

[math]dS_{OAB}\! \; = \;\! \frac{1}{2}\; r \; r d\theta = \frac{1}{2} \;| \vec{r} \times \vec{dr}| = \frac{1}{2} \;| \vec{r} \times \vec{v} | \; dt [/math]

Tym samym prędkość polową możemy wyrazić prez moment pędu:

[math]\frac{dS}{dt} \; = \; \frac{1}{2}\;| \vec{r} \times \vec{v} | \; = \; \frac{L}{2\;m } [/math]

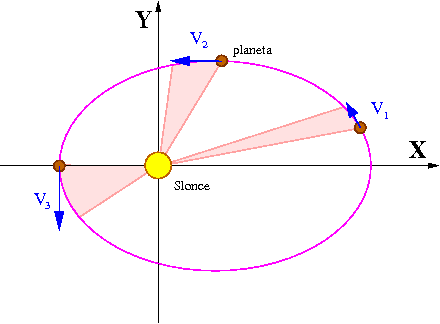
II prawo Keplera

W przypadku sił centralnych moment siły znika i moment pędu jest zachowany. Tym samym prędkość polowa musi być stała.

W ruchu pod działaniem sił centralnych prędkość polowa jest stała.