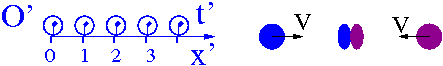FizykaI FMiN/Dynamika relativity
Dynamika relatywistyczna
Wprowadzenie
Zagadnienia ruchu ciał w mechanice nierelatywistycznej (Newtona/Galileusza) rozwiązywaliśmy w oparciu o równania ruchu. Ruch ciała jest zadany przez działające na nie siły zewnętrzne
- [math] \frac{d \vec{p}(t)}{dt} \; = \; \vec{F}(\vec{r}, \vec{v}, t) \; + \; \vec{F}_R[/math]
do których znajomości trzeba jeszcze dołączyć warunki początkowe
- [math] \vec{r}(t_0)= \vec{r}_0[/math]
- [math]\vec{v}(t_0)= \vec{v}_0 [/math]
Alternatywnie możemy korzystać z zasad zachowania. Dla układu izolowanego spełniona jest zasada zachowania pędu
- [math] \vec{P} \; = \; \sum_i \vec{p}_i \; = \; \sum_i m_i \vec{v}_i \; = \; const[/math]
natomiast w ruchu pod wpływem sił zachowawczych korzystaliśmy z zasady zachowania energii
- [math] E \; = \; E_p + E_k \; = \; E_p + \sum_i \frac{m_i v_i^2}{2} \; = \; const [/math]
Czy podejścia te można też wykorzystać w przypadku relatywistycznym?
Granice podejścia klasycznego
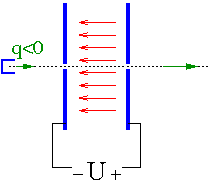
Rozważmy elektron przyspieszany w kondensatorze płaskim (najprostszy 'akcelerator' cząstek). Klasycznie przyspieszenie elektrony związane jest z natężeniem pola elektrycznego poprzez równanie ruchu postaci:
- [math] m\vec{a} \; = \; \vec{F} \; = \; q \vec{E} [/math]
Potrafimy współcześnie wytwarzać pola elektryczne sięgające
- [math]E \;\sim \; 10 \; MV/m \; = \; 10^{7}\; V/m [/math]
Dla elektronu masa i ładunek wynoszą odpowiednio:
- [math] m_e \; = \; 9.1 \cdot 10^{-31} kg \; = \; 0.5 \; MeV/c^2 [/math]
- [math] | q_e | \; \equiv \; 1 \; e \; = \; 1.6 \cdot 10^{-19} C [/math]
Tym samym uzyskalibyśmy przyspieszenie elektronu rzędu
- [math] a \; \approx \; 20\; m^{-1} \cdot c^2 \; \approx \; 2 \cdot 10^{18} m/s^2 [/math]
W podejściu klasycznym elektron powinien osiągnąć prędkość światła już po przebyciu [math]\Delta x \; \approx \; 2.5 \; cm[/math] !!!
Widzimy, że równanie ruchu w klasycznej postaci nie może obowiązywać w przypadku relatywistycznym, konieczna jest jego modyfikacja.
Pęd cząstki
Uogólnienie praw ruchu
Załóżmy, ze chcemy zachować klasyczną definicję siły opartą na II prawie Newtona
| [math]\vec{F} \; = \frac{d\vec{p}}{dt}[/math] |
Oznacza to jednak, że musimy zmienić definicję pędu, bo Newtonowska definicja
- [math] \vec{p} \; = \; m \vec{v}[/math]
ogranicza wartość pędu od góry ([math]v \lt c[/math]), a przecież wciaż mogą działać siły...
Doświadczenie myślowe
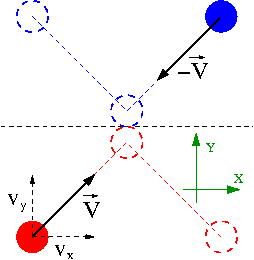
Rozważmy nie centralne zderzenie dwóch kul o jednakowej masie [math]m[/math] poruszających się z jednakowymi prędkościami V w układzie O:
Z symetrii zagadnienia, zarówno przed jak i po zderzeniu pędy obu kul muszą być równe co do wartości ale przeciwnie skierowane. Przejdźmy teraz do układu O' w którym jedna z kul porusza się tylko wzdłuż osi Y:
W wyniku zderzenia prędkości kul wzdłuż osi Y nie zmieniają wartości
a jedynie zwrot. Żeby zachowany był pęd wzdłuż osi Y
składowe pędu obu kul wzdłuż osi Y powinny być równe.
Prędności wzdłuż osi Y nie są równe. Wybór jednej z kul łamie symetrię zagadnienia !
Przesunięcia wzdłuż osi Y nie zmieniają się w transformacji Lorentza, ale zmienia się czas w jakim nastęują. Prędkość wzdłuż osi Y pierwszej kuli w układzie O':
- [math] V_{1,y} \; = \; \gamma \; V_y [/math]
Prędkość wzdłuż osi Y drugiej kuli:
- [math] V_{2,y} \; = \; \frac{V_y}{\gamma (1+\beta^2)} [/math]
gdzie [math]V_{x}[/math], [math]V_{x}[/math] to wartości współrzędnych prędkości w układzie O oraz
- [math] \beta = \frac{V_x}{c}[/math]
- [math] \gamma = \frac{1}{\sqrt{1-v_x^2/c^2}}[/math]
Widzimy więc, że klasyczne pędy obu kul nie są równe, czyli:
- [math] m\; V_{1,y} \; \ne \; m\; V_{2,y} [/math]
Z dodawania prędkości możemy wyznaczyć składową X prędkości drugiej kuli w układzie O':
- [math] V_{2,x} \; = \; \frac{-2 V_x}{\gamma (1+\beta^2)} [/math]
Gdybyśmy przeszli do układu, w którym druga kula porusza się tylko wzdłuż osi Y to sytuacja odwróciłaby się. Możemy więc związać prędkości obu kul zauważając, że prędkość wzdłuż osi Y drugiej kuli jest zmniejszona na skutek dylatacji czasu:
- [math] V_{2,y} \; = \; \frac{V_{1,y}}{\gamma'} [/math]
gdzie [math]\gamma'[/math] odpowiada transformacji między układami obu kul.
- [math]\gamma' = \frac{1}{\sqrt{1-V_{2,x}^2/c^2}}[/math]
Przyjmijmy teraz, że prędkości wzdłuż osi Y są nierelatywistyczne, [math]V_y \ll c[/math], ale prędkość wzdłuż osi X, [math]V_x \sim c[/math]. Wtedy możemy zapisać:
- [math] \gamma_{_1} \; V_{1,y} \; = \; \gamma_{_2} \; V_{2,y} [/math]
gdzie dla kuli poruszającej się tylko wzgłuż osi Y
- [math] \gamma_{_1} \; = \; 1 [/math]
zaś dla drugiej kuli
- [math] \gamma_{_2} = \frac{1}{\sqrt{1-V_{2}^2/c^2}}[/math]
Zasadę zachowania pędu możemy więc w naszym przypadku "uratować" modyfikując definicję pędu:
- [math] \vec{p} \; = \; m \cdot \gamma \cdot \vec{v} [/math]
Czy tak zdefiniowany pęd jest zachowany w ogólnym przypadku?
Zasada względności
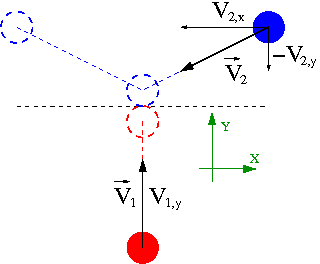
Wyrażenie na pęd dla cząstek relatywistycznych możemy też wyprowadzić z zasady względności (+ relatywistyczne składanie prędkości). Wyobraźmy sobie dwie identyczne kule lecące (w układzie O) z prędkościami [math]V_1[/math] i [math]V_2[/math] wzdłuż osi X:
Przyjmijmy, że w którymś momencie ciało 1 dogania ciało 2 i zlepia się z nim. Jaka będzie prędkość ciał po zlepieniu?
Klasycznie byłoby to [math]V_c = \frac{V_1+V_2}{2}[/math], co wynikało właśnie z zasady zachowania pędu! Jeśli odpowiemy na to pytanie w przypadku relatywistycznym to powinniśmy móc wnioskować o postaci wyrażenia na pęd...
Przejdźmy do układu odniesienia O' związanego z powstającym "zlepkiem".
Ponieważ kule są identyczne z symetrii zagadnienia oczekujemy, że w układzie tym będą miały prędkości równe co do wartości, lecz przeciwnie skierowane. Wiemy już jednak jak składają się prędkości! Prędkości w układzie O' wyrażają się przez [math]V_1[/math] i [math]V_2[/math], oraz prędkość O względem O' ([math]-V_c[/math])
Ze wzoru na składanie prędkości:
- [math] V \; = \; \frac{V_1 - V_c}{1 - \frac{V_1 V_c}{c^2}} [/math]
- [math] -V \; = \; \frac{V_2 - V_c}{1 - \frac{V_2 V_c}{c^2}} [/math]
(wartość ujemna prędkości odpowiada zwrotowi przeciwnemu do osi X)
Dla uproszczenia wprowadźmy prędkości względne:
- [math]\beta_1 = \frac{V_1}{c}[/math], [math]\beta_2 = \frac{V_2}{c}[/math] i [math]\beta_c = \frac{V_c}{c}[/math]
Rozwiązujemy ten układ równań i ostatecznie otrzymujemy wyrażenie
na prędkość zlepionych kul (poruszających się początkowo z prędkościami
[math]\beta_1[/math] i [math]\beta_2[/math]; pomijam dość żmudne
przekształcenia)
- [math] \beta_c \; = \; \frac{\beta_1\;\gamma_1 + \beta_2\;\gamma_2}{\gamma_1 + \gamma_2}[/math]
Dla symetrii pomnóżmy licznik i mianownik po lewej stronie przez [math]\gamma_c[/math]:
- [math] \frac{\beta_c \; \gamma_c}{\gamma_c} = \frac{\beta_1\;\gamma_1 + \beta_2\;\gamma_2} {\gamma_1 + \gamma_2} [/math]
Wartość ułamka nie zmienia się też jeśli licznik i mianownik pomnożymy przez tą samą liczbę ([math]M[/math] dla lewej i [math]m[/math] dla prawej strony):
- [math] \displaystyle \frac{\beta_c \; \gamma_c \; M}{\gamma_c \; M} \; = \; \frac{\beta_1\;\gamma_1 \;m + \beta_2\;\gamma_2\;m} {\gamma_1\;m + \gamma_2\;m} [/math]
Ale [math]M[/math] i [math]m[/math] są dowolne! Możemy zawsze tak dobrać stosunek ich wartości, żeby także liczniki i mianowniki po obu stronach równania były sobie równe:
- [math] \beta_c \; \gamma_c \; M \; = \; \beta_1\;\gamma_1 \;m + \beta_2\;\gamma_2\;m [/math]
- [math] \gamma_c \; M \; = \; \gamma_1\;m + \gamma_2\;m [/math]
Wychodząc z bardzo ogólnych założeń otrzymaliśmy dwa prawa zachowania!
Wykorzystaliśmy symetrię zagadnienia i zasadę względności oraz właściwy dobór współczynników [math]M[/math] i [math]m[/math].
Możemy uogólnić wprowadzone relacje na dowolną liczbę cząstek w stanie początkowym ([math]ini[/math]) i końcowym ([math]fin[/math]):
- [math] \sum_{i \in ini} \beta_i \; \gamma_i\; m_i \; = \; \sum_{j \in fin} \beta_j \; \gamma_j \;m_j [/math]
- [math] \sum_{i \in ini} \gamma_i\; m_i \; = \; \sum_{j \in fin} \gamma_j\; m_j [/math]
Ale jaki sens fizyczny mają przedstawione wyrażenia, czy możemy zidentyfikować poszczególne człony?
Relatywistyczna definicja pędu
W granicy małych prędkości ([math]\beta \ll 1[/math], [math]\gamma = 1[/math]) przedstawione równania sprowadzają sie do
- [math] c \; \sum_{i } \beta_i \; m_i \; = \; \sum_{i } m_i \; V_i \; = \; const [/math] - zasada zachowania pędu
- [math] \sum_{i} m_i \; = \; const [/math] - zasada zachowania masy
Jak poprzednio dochodzimy do wniosku, że relatywistyczne wyrażenie na pęd cząstki to
| [math]p \; = \; m \;c \;\gamma \; \beta \; = \; m \; \gamma \; V[/math] |
Wprowadzone współczynniki [math]m[/math] są miarą bezwładności ciał i nazywamy je masą.
Jedną z mas mogliśmy ustalić dowolnie - odpowiada to wyborowi wzorca masy.
Masy pozostałych cząstek można następnie wyznaczyć w oddziaływaniu ze wzorcem (z wyprowadzonych praw zachowania).
Ruch pod wpływem stałej siły
Równanie ruchu
Jak już wspominaliśmy, chcemy zachować klasyczną definicję siły opartą na II prawie Newtona:
- [math] \vec{F} \; = \; \frac{d\vec{p}}{dt} [/math]
gdzie jednak pęd definiujemy teraz jako
- [math] \vec{p} \; = \; m \; \gamma \; \vec{v} \; = \; m c\; \gamma \; \vec{\beta}[/math]
współczynnik Lorentza [math]\gamma \; = \; \frac{1}{\sqrt{1-\beta^2}}[/math]
W przypadku ruchu prostoliniowego otrzymujemy w wyniku różniczkowania
- [math] F \; = \; \frac{d}{dt} \left(mc \; \gamma \; \beta \right) \; = \; mc \; \gamma^3 \; \frac{d\beta}{dt} [/math]
Widzimy, że w przypadku relatywistycznym przyspieszenie maleje jak [math]\gamma^{-3}[/math] !
Wróćmy do zagadnienia eletronu w jednorodnym polu elektrycznym.
Możemy rozwiązać teraz zagadnienie ruchu pod wpływem stałej siły
elektrycznej [math]F = qE[/math].
Przekształcając otrzymane równanie
- [math] \frac{d\beta}{dt} \; = \; \frac{q E}{mc} \; (1 - \beta^2)^{3/2} [/math]
możemy rozdzielić zmienne
- [math]\frac{d\beta}{(1 - \beta^2)^{3/2}}\; = \; \frac{q E}{mc} \; dt [/math]
Całkujemy podstawiając [math]\beta = \sin u [/math]:
- [math] \int \frac{du}{\cos^2 u}\; = \; \frac{q E}{mc} \int dt [/math]
i otrzymujemy rozwiązanie postaci
- [math] \tan u \; = \; \frac{q E}{mc} \cdot t [/math]
przyjmując, że cząstka spoczywała w [math]t=0[/math].
Korzystając teraz z tożsamości trygonometrycznej: [math]\sin u \; = \; \frac{\tan u }{\sqrt{1 + \tan^2 u}}[/math]
otrzymujemy rozwiązanie w postaci:
- [math] \beta(t) \; = \; \frac{\alpha t }{\sqrt{1 + (\alpha t)^2}} [/math]
gdzie: [math] \alpha \; = \; \frac{q E}{mc} [/math]
W naszym przykładzie ([math]e^-[/math] w polu [math]10\frac{MV}{m}[/math]) otrzymujemy
- [math]\alpha \sim 6\cdot 10^9 \; s^{-1}[/math]
skala czasowa po jakiej prędkość stanie się porównywalna z prędkością światła dana jest przez
- [math]\alpha^{-1} \sim 0.17\;ns[/math]
Zależność prędkości od czasu
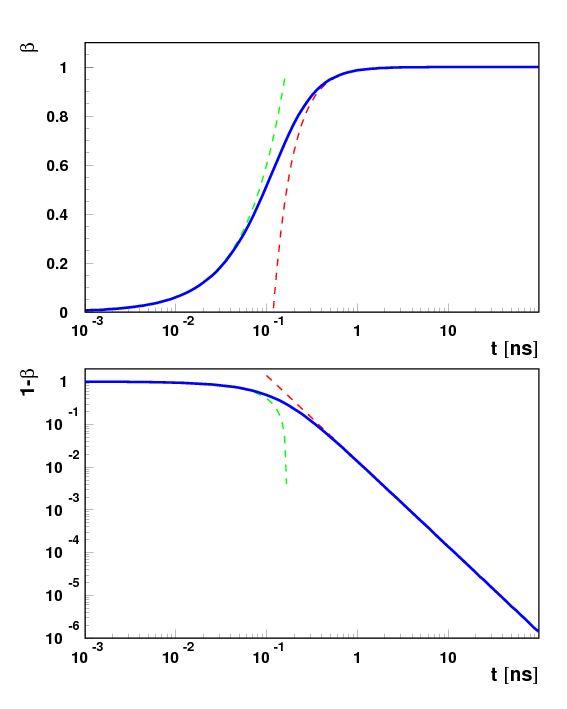
Rysunek poniżej pokazuje zależność uzyskanej przez elektron prędkości od czasu. Do czasów rzędu [math]0.1\;ns[/math] ruch można opisywać klasycznie (zielona przerywana linia):
Pokazana jest również różnica między prędkościa światła a prędkością
uzyskaną przez elektron po czasie t.
Prędkość elektronu nigdy nie osiągnie prędkości światła.
W granicy [math]\alpha \; t \gg 1[/math]:
- [math] 1 - \beta(t) \; \approx \; \frac{1}{2 \alpha^2 t^2 } [/math]
(zależność ta została przedstawiona na rysunku czerwoną przerywaną linią).
Mimo, że nigdy nie osiągniemy [math]\beta = 1[/math] pęd elektronu będzie rósł liniowo z czasem
- [math]p(t) \; = \; m c \; \alpha\cdot t [/math]
Zależność położenia od czasu
Wyrażenie na prędkość możemy zapisać w postaci:
- [math] \frac{dx}{dt} \; = \; \frac{c \;\alpha t }{\sqrt{1 + (\alpha t)^2}} [/math]
Całkując otrzymujemy
- [math] x(t) \; = \; \int dx \; = \; \frac{c}{\alpha}
\int \frac{\alpha t \; d(\alpha t) }{\sqrt{1 + (\alpha t)^2}}[/math]
- [math] \; = \; \frac{c}{\alpha} \left(\sqrt{1 + (\alpha t)^2} -1 \right)[/math]
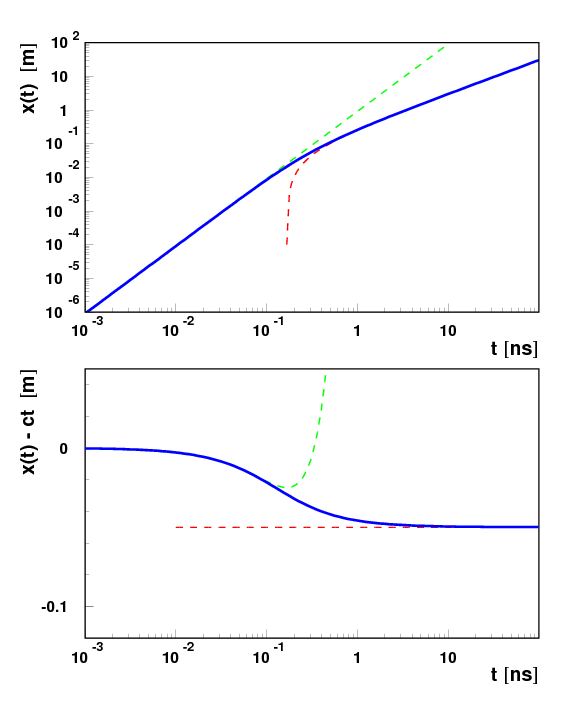
Uzyskane rozwiązanie przedstawione jest na rysunku poniżej.
Tak jak poprzednio zielona przerywana linia odpowiada rozwiązaniu klasycznemu, zaś czerwona przerywana - rozwiązaniu asymptotycznemu. W granicy [math]\alpha \; t \gg 1[/math]:
- [math] x(t) \; \approx \; c\;t \; - \frac{c}{\alpha} [/math]
czyli elektron porusza się ruchem jednostajnym z prędkościa praktycznie równą prędkości światła (cząstka ultrarelatywistyczna).
Czynnik [math]\frac{c}{\alpha}[/math] odpowiada odległości o jaką impuls światła wysłany w chwili [math]t=0[/math] wyprzedzi rozpędzany elektron. W naszym przykładzie to tylko o 5 cm !!!
Energia relatywistyczna
Dla ruchu ciała pod wpływem stałej siły otrzymaliśmy wyrażenia:
- [math] x(t) \; = \; \frac{c}{\alpha} \left(\sqrt{1 + (\alpha t)^2} -1 \right) [/math]
- [math] \beta(t) \; = \; \frac{\alpha t }{\sqrt{1 + (\alpha t)^2}} [/math]
gdzie [math]\alpha \; = \; \frac{F}{mc} [/math]
Można zauważyć, że czynnik Lorentza:
- [math] \gamma(t) \; = \; \frac{1}{\sqrt{1 -\beta^2(t)}} \; = \; \sqrt{1 + (\alpha t)^2} [/math]
wstawiając do wyrażenia na [math]x(t)[/math] otrzymujemy
- [math] x(t) \; = \; \frac{mc^2}{F} ( \gamma - 1 ) [/math]
Uzyskana przez przyspieszaną cząstkę energia kinetyczna jest równa pracy wykonanej przez siłę F na drodze [math]x(t)[/math]. Otrzymujemy:
- [math] E_k(t) \; = \; F\cdot x(t) \; = \; m\; c^2 \; \left( \gamma(t) - 1 \right) [/math]
Uzyskaną poprzednio zasadę zachowania:
- [math] \sum_{i} \gamma_i\; m_i \; c^2 \; = \; const [/math]
możemy więc przepisać w postaci:
- [math] \sum_{i} \left[ m_i \; c^2 \; ( \gamma_i - 1) \; + \;m_i \; c^2 \right] \; = \; const [/math]
- [math]\sum_{i} \left[ \; E_{k,i}\; + \;E_{0,i} \; \right] \; = \; const [/math]
Gdzie:
- [math]E_{k} = m\; c^2 \; \left( \gamma - 1 \right)[/math] - energia kinetyczna
- [math]E_{0} = m\; c^2 [/math] - energia spoczynkowa ciała
Konieczność wprowadzenia energii spoczynkowej wynika z otrzymanej postaci zasady zachowania energii!
Energia całkowita:
|
[math]\displaystyle E \;=\; E_{k}\; +\; E_{0} = \gamma \cdot m\; c^2 [/math] |
Granica klasyczna
Wyrażenie na energię kinetyczną można zapisać w postaci
- [math] E_k \; = \; m\; c^2 \; ( \gamma - 1 ) \; = \; m\; c^2 \; \left( \frac{1}{\sqrt{1-\beta^2}} - 1 \right) [/math]
W granicy małych prędkości ([math]\beta \ll 1[/math]) korzystamy ze wzorów na rozwinięcie w szereg:
- [math] \sqrt{1+\varepsilon} \; \approx \; 1 + \frac{1}{2} \varepsilon - \frac{1}{8} \varepsilon^2 + \ldots [/math]
- [math] \frac{1}{1+\varepsilon} \; \approx \; 1 - \varepsilon + \varepsilon^2 + \ldots [/math]
W szczególności dla czynnika Lorentza
- [math] \gamma \; = \; \frac{1}{\sqrt{1-\beta^2}} \; \approx \; 1 + \frac{1}{2} \beta^2[/math]
Wyrażenie na energię kinetyczną w granicy [math]\beta \ll 1[/math] przyjmuje więc postać
- [math] E_k \; = \; m\; c^2 \; ( \gamma - 1 ) \; = \; (1 + \frac{1}{2} \beta^2 \;- \;1) \; = \; \frac{1}{2} m\; c^2 \;\beta^2\; = \; \frac{1}{2} m\; V^2 [/math]
Odtwarzamy klasyczne wyrażenie na energię kinetyczną!
Zasada zachowania energii i pędu
Zdefiniowaliśmy energię całkowitą ciała:
- [math] E \; = \; \gamma \cdot m\; c^2 [/math]
oraz jego pęd:
- [math] \vec{p} \; = \; \gamma \cdot m\; \vec{V} [/math]
- [math] \vec{p} \; = \; \vec{\beta} \;\gamma \cdot m\;c [/math]
gdzie [math] \vec{\beta} \; = \; \frac{\vec{V}}{c} [/math]
Wychodząc z reguły składania prędkości (która z kolei wynikała z zasady bezwładności i zasady względności), wykorzystując symetrię rozważanego zagadnienia (zasada względności) oraz możliwość doboru współczynników opisujących bezwładność ciała (masę) otrzymaliśmy:
- zasadę zachowania enegrii
- [math] \sum_{i } E_i \; = \; \sum_{i } \gamma_i \; m_i\; c^2 \; = \; const [/math]
- zasadę zachowania pędu
- [math] \sum_{i} \vec{p}_i \; = \; \sum_{i } \gamma_i \cdot m_i\; \vec{V_i} \; = \; const [/math]
Zasady te wyprowadziliśmy dla procesu zderzenia, ale okazuje się, że są one dużo bardziej ogólne.
Zasady te obowiązują we wszystkich znanych nam procesach!!!
Zasada zachowania energii ma jednak swoją "cenę". W procesie
zderzenia nieelastycznego:
Z zasady zachowania energii otrzymujemy:
- [math] E_c \; = \; E_1 \; + \; E_2 [/math]
- [math] M \; c^2 \; = \; \gamma \; m \; c^2 \; + \;\gamma \; m \; c^2 [/math]
- [math] M \; = \; 2 \; \gamma \; m [/math]
Widzimy, że masa "zlepka" jest zawsze większa niż suma mas cząstek!
- [math]M \gt m + m [/math]
W świecie relatywistycznym przestaje obowiązywać zasada zachowania masy!
Energia kinetyczna zderzających się cząstek została zamieniona na energię wewnętrzną, co jest równoważne ze wzrostem masy (energii spoczynkowej) "zlepka".
Jednostki
Energia jaką zyskuje ładunek [math]q[/math] przy przejściu różnicy potencjały [math]U[/math] wynosi
- [math] \Delta E \; = \; U \cdot q [/math]
Dlatego jako naturalną jednostką energii w fizyce cząstek przyjęto 1 elektronowolt (1 eV). Jest to energia jaką zyskuje cząstka o ładunku 1 e (ładunek elementarny) przy przejściu różnicy potencjału 1 V.
W jednostkach układu SI
- [math]1 \; e \; = \; 1.6 \cdot 10^{-19} \; C \; \Rightarrow \; 1 \; eV \; = \; 1.6 \cdot 10^{-19} \; J[/math]
Najczęściej wykorzystkujemy jednostki pochodne:
- [math]1 keV = 10^{3} \; eV [/math],
- [math]1 MeV = 10^{6} \; eV [/math],
- [math]1 GeV = 10^{9} \; eV [/math].
Ponieważ masa jest równoważna energii spoczynkowej, jednostkę energii możemy też przyjąć za jednostkę masy ([math]E = m c^{2}[/math]; [math]c \equiv 1[/math])
- [math] 1\; eV/c^{2}\; \equiv \; 1 \; eV \; = \; 1.8 \cdot 10^{-36}\; kg [/math]
Przykładowe masy (energie spoczynkowe) cząstek wynoszą
| cząstka | symbol | masa | |
|---|---|---|---|
| elektron | e | 511 keV | (9.1 [math]\cdot 10^{-31}[/math] kg) |
| proton | p | 938 MeV | (1.7 [math]\cdot 10^{-27}[/math] kg) |
| neutron | n | 940 MeV | |
| kwark top | t | 173 GeV | |
| bozony pośredniczące | [math]W^{\pm}[/math] | 80.4 GeV | |
| [math]Z^{\circ}[/math] | 91.2 GeV | ||
Transformacja
Energia spoczynkowa cząstki wynosi:
- [math] E_\circ \; = \; m\; c^2[/math]
Energia całkowita:
- [math] E \; = \; E_\circ \;+\; E_k \; = \; m\; c^2 \cdot \gamma [/math]
Pęd cząstki dany jest przez wyrażenie:
- [math] p \; = \; m\; c \cdot \beta \; \gamma [/math]
W układzie własnym cząstki pęd
- [math]p_\circ \; = \; 0[/math]
zgodnie z definicją układu środka masy.
Możemy zauważyć, że:
- [math] E \; = \; \gamma \; E_\circ [/math]
- [math] p\;c \; = \; \beta \; \gamma \; E_\circ [/math]
Jeśli cząstka porusza się wzdłuż osi [math]X[/math]:
- [math]E \; = \; \gamma \; E_\circ [/math]
- [math]c\; p_x \; = \; \beta \; \gamma \; E_\circ [/math]
- [math]c\; p_y \; = \; 0 [/math]
- [math]c\; p_z \; = \; 0 [/math]
Formalnie możemy więc zapisać ([math]p_{\circ} = p_{\circ,x} = p_{\circ,y}= p_{\circ,z}=0[/math])
- [math] \left(\begin{array}{c} E \\ c\;p_x \\ c\;p_y \\ c\;p_z \end{array}\right) \; = \; \left(\begin{array}{c} \gamma \; E_\circ \; + \; \gamma \; \beta \; c \; p_{\circ,x} \\ \gamma \; \beta \; E_\circ \; + \; \gamma \; c \; p_{\circ,x} \\ c \; p_{\circ,y}\\ c \; p_{\circ,z} \end{array}\right) \; = \; \left(\begin{array}{cccc} \gamma & \gamma \; \beta & 0 & 0 \\ \gamma \; \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} E_\circ \\ c \; p_{\circ,x}\\ c \; p_{\circ,y}\\ c \; p_{\circ,z} \end{array}\right) [/math]
Okazuje się, że energia i pęd podlegają, przy zmianie układu odniesienia, transformacji Lorentza identycznej z transformacją czasu i położenia.
Masa niezmiennicza
Z definicji czynnika Lorentza
- [math] \gamma \; = \; \frac{1}{\sqrt{1-\beta^2}} [/math]
otrzymujemy tożsamość
- [math]\gamma^2 - \beta^2 \gamma^2 \; = \; \gamma^2 ( 1 - \beta^2 ) \; = \; 1 [/math]
Mnożąc obie strony przez energię spoczynkową
- [math] \gamma^2 \; E_\circ^2 \; - \; \beta^2 \gamma^2 \; E_\circ^2 \; = \; \; E_\circ^2 [/math]
Czyli:
| [math]E^2 \; - \; c^2 \; p^2 \; = \; m^2 \; c^4[/math] |
Związek ten jest słuszny niezależnie od prędkości cząstki, czyli niezależnie od układu odniesienia. Wyrażenie:
- [math] s \; = \; M^2 \; c^4 \; = \; E^2 \; - \; c^2 \; p^2 [/math]
jest niezmiennikiem transformacji Lorentza (nie zależy od wyboru układu odniesienia) dla dowolnego układu fizycznego. Wartość
- [math]M \equiv \sqrt{s}[/math]
nazywamy masą niezmieniczą układu (masą inwariantną). Jest to kluczowa wielkość w opisie zderzeń relatywistycznych.
Transformacja Lorentza
Transformacja Lorentza ma zastosowanie do wszystkich czterowektorów:
- czterowektora położenia (w czasoprzestrzeni): [math](ct, x, y, z)[/math]
- czterowektora energii-pędu ("czteropęd"): [math](E, c p_x, c p_y, c p_z)[/math]
- czteropotencjału pola elektromagnetycznego: [math](\Phi, A_x, A_y, A_z)[/math]
- gdzie pola elektryczne i magnetyczne zdefiniowane są jako [math]\vec{E} = - grad \Phi \; - \;\frac{1}{c} \frac{\partial \vec{A}}{\partial t}[/math] i [math]\vec{B} = rot \vec{A}[/math]
- różnicy dwóch czterowektorów (np. odstęp między zdarzeniami, przekaz czteropędu...)
Niezmiennikiem transformacji Lorentza jest "kwadrat" każdego czterowektora
- [math] \left| A^{(4)} \right|^2 \; = \; A_0^2 - \left| \vec{A} \right|^2 \; = \; A_0^2 - A_x^2 - A_y^2 - A_z^2 [/math]
W przypadku wektora różnicy współrzędnych jest to interwał:
- [math] s_{AB} = (\Delta t)^2 - (\Delta x)^2 - (\Delta y)^2 - (\Delta z)^2 [/math]
w przypadku wektora energi-pędu jest to masa niezmiennicza:
- [math] M^2 = E^2 - p_x^2 - p_y^2 - p_z^2 [/math]
Foton
Zjawisko fotoelektryczne
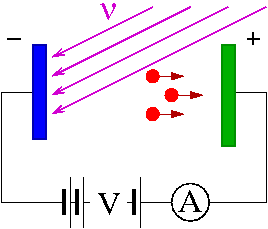
Zjawisko fotoelektryczne zostało odkryte (podobno przypadkowo) przez Hertza w 1887 r. Polega ono na tym, że światło padając na metalową płytkę powoduje uwalnianie elektronów i umożliwia przepływ prądu pomiędzy dwoma elektrodami
Doświadczenia wskazały, że energia uwalnianych elektronów zależy
wyłącznie od częstości światła (długości fali)
i materiału katody. Powyżej pewnej
długości światła elektrony nie były wybijane - prąd nie płynął.
Nie można tego było wytłumaczyć w ramach falowego opisu
rozchodzenia się światła, który przewidywał, że prąd zależy wyłącznie
od natężenia światła, a nie zależy od częstości !
Zjawisko fotoelektryczne wyjaśnił
Einstein (1905)
wprowadzając pojęcie kwantu światła dziś nazywanego fotonem.
Energia foto-elektronów wybijanych z katody
- [math] E_e \; = \; E_\gamma \; - \; W \; = \; h\; \nu \; - \; W [/math]
gdzie [math]W[/math] to "praca wyjścia", minimalna energia potrzebna do uwolnienia elektronu z metalu (zależy od materiału katody) zaś [math]\nu [/math] to częstość fali światła. Energia jaką niesie pojedynczy foton (i przekazuje elektronowi)
- [math] E_\gamma \; = \; h\; \nu [/math]
Natura światła
Fotony to kwanty promieniowania elektromagnetycznego. Przenoszą oddziaływania między cząstkami naładowanymi. Mają naturę korpuskularno-falową, czyli są jednocześnie
- falą elektromagnetyczną, opisaną równaniami Maxwella
- rozchodzącą się z prędkością [math]\displaystyle c = \frac{1}{\sqrt{\epsilon_\circ \mu_\circ}} [/math]
- podlegającą interferencji, dyfrakcji, załamaniu
- cząstką o ustalonej energii i pędzie, ale zerowej masie, [math]m_\gamma \equiv 0 \; \Leftrightarrow \; \beta \equiv 1[/math]
- mogą zderzać się z innymi cząstkami, być pochłaniane lub rozpraszane
Im wyższa częstość (mniejsza długość fali)
promieniowania, tym wyższa energia
pojedyńczego fotonu i wyraźniejsze efekty korpuskularne
- [math] E_\gamma \; = \; p_\gamma \; c \; = \; h\; \nu \; = \; \frac{hc}{\lambda} [/math]
przy czym częstość i długość fali związane są relacją [math] \lambda \cdot \nu = c[/math]
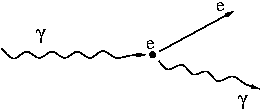
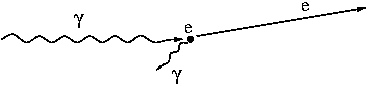
W zjawisku fotoelektrycznym, foton "zderza się" z elektronem,
- [math] \gamma + e^- \rightarrow e^- [/math]
i przekazuje mu energię konieczną do opuszczenia metalu (tzw. proces typu [math]2 \rightarrow 1[/math])
Efekt Dopplera
Klasycznie mamy dwa różne przypadki:
- źródło o częstości [math]\nu[/math] poruszające się z prędkością [math]v[/math] względem ośrodka. Częstość dźwięku mierzona przez nieruchomego obserwatora
- obserwator porusza się z prędkością [math]v[/math] względem ośrodka i źródła dżwięku
Jak już pokazaliśmy na poprzednim wykładzie w przypadku światła sytuacja jest symetryczna (brak ośrodka) i mierzona częstość wyraża się wzorem
- [math] \nu' \; = \; \nu \; \sqrt{\frac{1-\beta}{1+\beta}}[/math]
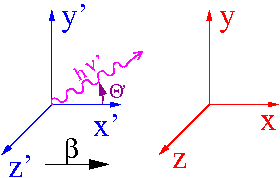
W przypadku ogólnym (dowolny kierunek ruchu źródła względem obserwatora) mierzone przesunięcie długości fali:
- [math] \lambda' \; = \; \; = \; \gamma \left( 1 - \beta \; \cos\Theta \right) \; \lambda [/math]
gdzie [math]\Theta[/math] to rejestrowany przez obserwatora kierunek lotu fotonu (a [math]\pi-\Theta[/math] to kierunek z którego jest obserwowany).
Alternatywne podejście
Wyrażenia na relatywistyczny efekt Dopplera (dla światła) wynikają wprost z transformacji Lorentza dla energii i pędu fotonu.
Przyjmijmy, że foton o energii [math]E' = h\nu '[/math] emitowany jest pod kątem [math]\theta '[/math] w układzie O'. Składowe pędu tego fotonu dane są przez
- [math] p'_x = E' \cos \theta '[/math]
- [math] p'_y = E' \sin \theta '[/math]
W układzie O z transformacji Lorentza uzyskujemy:
- [math] h\nu = E \; = \; \gamma\; E' + \beta \; \gamma \; p'_x [/math]
- [math] \; = \; h \nu\;' \; \gamma \; ( 1 + \beta \cos \theta ') [/math]
Dla [math]\theta' = 0[/math], czyli emisji fotonu zgodnie z kierunkiem ruchu (źródło przybliża się do obserwatora) mamy:
- [math] \nu \; = \; \nu\;' \frac{ 1 + \beta}{\sqrt{1 - \beta^2}} \; = \; \nu\;' \sqrt{\frac{ 1 + \beta}{1 - \beta}} [/math]
częstość (energia) fotonu rośnie
Dla [math]\theta' = \pi[/math], czyli gdy foton emitowany jest przeciwnie do kierunku ruchu źródła (źródło oddala się od obserwatora) otrzymujemy:
- [math] \nu \; = \; \nu\;' \frac{ 1 - \beta}{\sqrt{1 - \beta^2}} \; = \; \nu\;' \sqrt{\frac{ 1 - \beta}{1 + \beta}} [/math]
czyli częstość (energia) fotonu maleje (zgodnie z wynikiem uzyskanym poprzednio w podejściu kinematycznym.
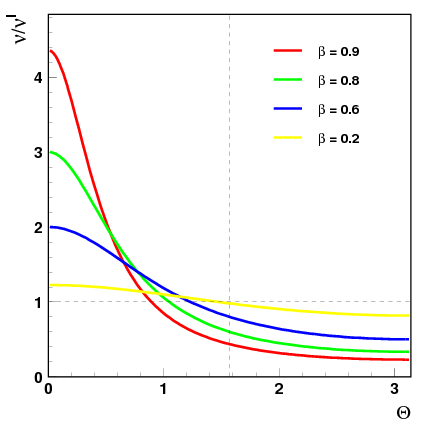
Rozkłady kątowe
Zależność obserwowanej częstości od kąta emisji fotonu przedstawiona jest na rysunku poniżej
Dla fotonów emitowanych prostopadle do kierunku ruchu, [math]\theta'=\frac{\pi}{2}[/math], obserwujemy wzrost częstości, [math]\nu = \gamma \; \nu ' \gt \nu'[/math] (poprzeczny efekt Dopplera).
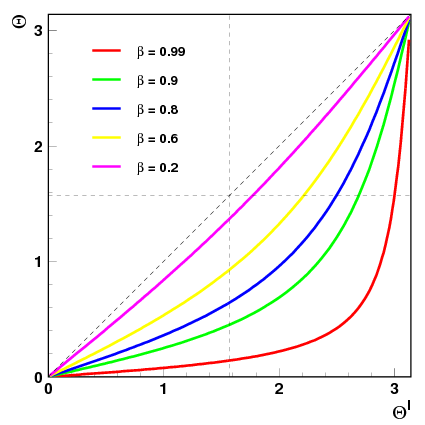
Obserwowany kąt lotu fotonu (kąt w jakim foton porusza się w układzie
obserwatora) jest związany z kątem emisji zależnością:
- [math] \cos \theta = \frac{p_x}{E} \; = \; \frac{\beta + \cos \theta'}{1 + \beta \cos \theta '} [/math]
która jest pokazana (dla wybranych wartości prędkości źródła) poniżej
W szczególności dla fotonu emitowanego pod kątem prostym, [math]\theta' = \frac{\pi}{2}[/math], obserwowany kąt propagacji fotonu dany jest przez [math]\cos \theta = \beta [/math], czyli jest mniejszy od kąta prostego ([math]\theta \lt \frac{\pi}{2}[/math]).
Zauważmy, że izotropowe promieniowanie szybko poruszającego się ciała będzie skolimowane w kierunku ruchu. Im szybciej ciało się porusza w tym węższym stożku będzie emitować większość promieniowania.
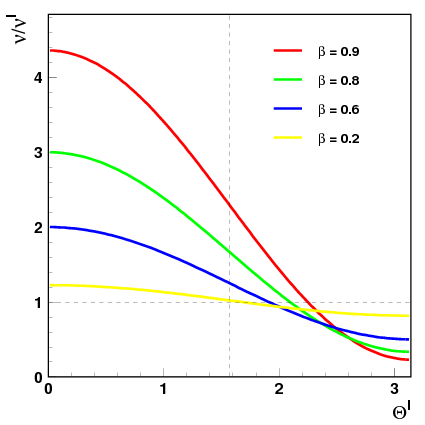
Do tej pory rozważaliśmy obserwowaną częstość w funkcji kąta emisji fotonu (kąt mierzony w układzie źródła)
- [math]\nu \; = \; \nu\;' \; \gamma \; ( 1 + \beta \cos \theta ')[/math]
Możemy jednak zastosować odwrotną transformację Lorentza i przedstawi energię w funkcji kąta detekcji (kąta propagacji fotonu mierzonego w układzie obserwatora):
- [math]\nu \; = \; \frac{\nu\;'} { \gamma \; ( 1 - \beta \cos \theta )} [/math]
Fotony rejestrowane pod kątem [math]\theta=\frac{\pi}{2}[/math] mają częstość niższą niż częstość źródła, [math]\nu = \frac{\nu '}{\gamma} \lt \nu'[/math].
Zależność częstości od kąta detekcji
Efekt Comptona
W wyniku rozpraszania w materii, promieniowanie X stawało się mniej przenikliwe, zmieniało długości fali. Opis tego zjawiska, na gruncie teorii Einsteina (korpuskularnej teorii światła), zaproponował w 1923 roku A.H.Compton.
Fotony promieniowania X
rozpraszają się na elektronach w atomie
oddając im część swojej energii.
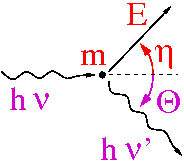
Relatywistyczne zderzenie dwóch ciał, tak samo jak w przypadku cząstek, możemy rozważyć z punktu widzenia zasad zachowania.
Możemy wypisać następujące relacje:
- zachowanie energii
- [math] h\nu + m \; = \; h\nu' + E [/math]
- zachowanie pędu wzdłuż kierunku ruchu fotonu
- [math] h\nu \; = \; h\nu' \cos \theta + p \cos \eta [/math]
- zachowanie prostopadłej składowej pędu
- [math] 0 \; = \; h\nu' \sin \theta - p \sin \eta [/math]
Przekształcając otrzymujemy:
- [math] E \; = \; h(\nu - \nu') + m [/math]
- [math] p \cos \eta \; = \; h(\nu - \nu' \cos \theta ) [/math]
- [math] p \sin \eta \; = \; h\nu' \sin \theta [/math]
Podnosząc stronami do kwadratu i zestawiając do masy elektronu:
- [math] m^2 \; = \; E^2 - p^2 [/math]
- [math] \; = \; \left( h(\nu - \nu') + m \right)^2 - h^2 \left( \nu - \nu' \cos \theta \right)^2 - \left( h\nu' \sin \theta \right)^2 [/math]
- [math] \; = \; m^2 + h^2\nu^2 + h^2 \nu'^2
- 2h^2\nu \nu' + 2mh(\nu - \nu') [/math]
- [math] - h^2 \nu^2 + 2h^2 \nu \nu' \cos \theta - h^2 \nu'^2 \cos^2 \theta - h^2 \nu'^2 \sin^2 \theta [/math]
Widzimy, że człony kwadratowe w częstości upraszczają się. Otrzymujemy
- [math] m \; h \nu \; = \; h \nu' \left(m + h\nu (1 - \cos \theta) \right) [/math]
Energia rozproszonego fotonu będzie więc równa
- [math] h \nu' \; = \; \frac{ h \nu }{1 + \frac{h\nu}{m}(1 - \cos \theta) }[/math]
zaś jego długość fali
- [math] \lambda' \; = \; \lambda \; + \; \frac{h}{m\;c} (1 - \cos \theta) [/math]
Widzimy, że przesunięcie długości fali zależy tylko od kąta rozproszenia, nie zależy od początkowej długości fali. Wielkość przesunięcia zależy od wartości
- [math]\frac{h}{m\;c} = 2.43\cdot10^{-12}m = 2.43\; pm[/math]
zwanej Comptonowską długością fali.
Małe energie fotonów
W granicy małych energii fotonu [math] h \nu \ll m[/math]
- [math] h \nu' \; = \; h \nu \; \frac{ m }{m + h\nu(1 - \cos \theta) } \; \approx \; h \nu [/math]
czyli foton rozprasza się bez straty energii. Odpowiada to klasycznemu zderzeniu "pocisku", [math]m_1[/math], z dużo cięższą "tarczą", [math]m_2 \gg m_1[/math]. Foton zachowuje energię, ale zmienia się wektor pędu (kierunek !) Przykładem jest odbicie światła widzialnego, [math]h \nu = 1.8 - 3.1 eV[/math] (700 nm - 400 nm)
Z kolei energia rozproszonego elektronu wynosi:
- [math] E \; = \; h\nu \; - \; h\nu'\; + \; m [/math]
- [math] \; = \; \frac{h\nu ( h \nu + m ) ( 1 - \cos \theta) + m^2 } {h\nu ( 1 - \cos \theta) + m } [/math]
W granicy małych energii padającego fotonu, [math] h \nu \ll m[/math]:
- energia elektronu:
- [math] E \; \approx \; m [/math]
- pęd rozproszonego elektronu:
- [math] p \; \approx \; h\nu \; \sqrt{2 ( 1 - \cos \theta )} [/math]
Duże energie fotonów
W granicy dużych energii padającego fotonu
[math] h \nu \gg m[/math]
(przyjmując [math]\cos \theta \ne 1[/math],
czyli [math]\theta \ne 0[/math]) otrzymujemy
- [math] h \nu' \; \approx \; \frac{ m }{1 - \cos \theta } \; \rightarrow \; 0 [/math]
- [math] E \; \approx \; h \nu \; + \; m [/math]
czyli foton przekazuje spoczywającemu elektronowi praktycznie całą swoją energię.
Odpowiada to klasycznemy zderzeniu ciał o równych masach (zakładając zderzenie centralne i elastyczne). Dla [math]h \nu \gg m[/math] masę elektronu można pominąć, elektron, tak jak foton, można traktować jako cząstkę bezmasową.
Rozpraszanie na wiązce elektronów
W rozpraszaniu na spoczywającym elektronie najniższą energię będzie miał foton rozproszony "do tyłu" ([math]\cos \theta = -1 [/math]):
- [math] h \nu' \; = \; \frac{ h \nu \cdot m }{ 2 h \nu + m } \; \lt \; h \nu [/math]
To, że foton zawsze traci energię zwiazane jest jednak z wyborem układu odniesienia! (układ związany z elektronem)
Możemy jednak rozważyć rozpraszanie fotonów o energii [math]h \nu[/math] na przeciwbieżnej wiązce elektronów o energii [math]E_e \gg m[/math].
Współczynniki transformacji Lorentza do układu elektronu:
- [math] \gamma \; = \; \frac{E_e}{m} [/math]
- [math] \beta \; \approx \; 1 [/math]
Energia fotonu w układzie elektronu wyniesie więc:
- [math] h\nu^\star \; = \; \gamma ( 1 + \beta ) h \nu [/math]
- [math] \; \approx \; \frac{2 E_e}{m} \cdot h \nu \; \gg \; h \nu [/math]
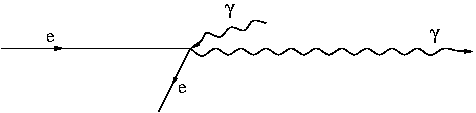
Jeśli teraz w układzie elektronu foton rozprasza się "do tyłu" ([math]\cos \theta = -1 [/math]) to jego energia po rozproszeniu:
- [math] h \nu^{\star \prime}
\; = \; \frac{ h \nu^\star \cdot m }{ 2 h \nu^\star + m } [/math]
- [math] \; \approx \; \frac{2 E_e \; h \nu \cdot m }{4 E_e \; h \nu + m^2} [/math]
Wracając teraz do układu laboratoryjnego: (transformacja odwrotna, ale i pęd foton zmienił kierunek)
- [math] h \nu' \; \approx \; \frac{2 E_e}{m} \cdot h \nu^{\star \prime}[/math]
Otrzymujemy:
- [math] h \nu' \; \approx \; E_e \cdot \frac{4 E_e \; h \nu }{4 E_e \; h \nu + m^2} [/math]
W przypadku wysokiej energii wiązki, [math]4 E_e \; h \nu \gg m^2 [/math], elektron może przekazać fotonowi większość swojej energii.
Przykład: dla [math]E_e = 250 GeV[/math] (planowana energia przyszłego akceleratora ILC) i [math]h\nu = 1 eV[/math] (podczerwień) możemy otrzymać wiązkę fotonów o energii [math]h\nu' \approx 200 GeV[/math].