FizykaI FMiN/Dynamika equations: Różnice pomiędzy wersjami
SuperAdmin (dyskusja | edycje) |
|||
| Linia 859: | Linia 859: | ||
<center> | <center> | ||
| − | [[image:Magnus_effect. | + | [[image:Magnus_effect.png|300px]] |
</center> | </center> | ||
Aktualna wersja na dzień 14:37, 10 cze 2015
Dynamika: równania ruchu
Równania ruchu
Podstawowym zagadnieniem dynamiki jest rozwiązywanie równań ruchu, czyli określanie ruchu ciała ze znajomości działających na nie sił.
Siła działająca na ciało może zależeć od
położenia i
prędkości cząstki
oraz czasu
⇒ równanie ruchu:
- [math] m \; \frac{d^2 \vec{r}(t)}{dt^2} \; = \; \vec{F}(\vec{r}, \vec{v}, t) [/math]
Ogólne rozwiązanie ma sześć stałych całkowania:
- [math] \vec{r} \; = \; \vec{r}\; (t,C_1, C_2, \ldots ,C_6)[/math]
Aby ściśle określić ruch ciała musimy poza rozwiązaniem równań ruchu wyznaczyć wartości wolnych parametrów (w ogólnym przypadku sześciu). Najczęściej dokonujemy tego określając warunki początkowe:
- [math] \vec{r}_0 \; = \; \vec{r}\; (t_0) [/math]
- [math] \vec{v}_0 \; = \; \vec{v}\; (t_0) [/math]
- gdzie [math]t_0[/math] - wybrana "chwila początkowa"
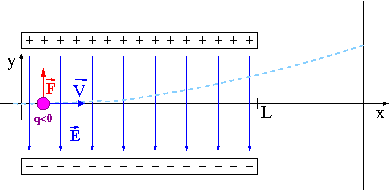
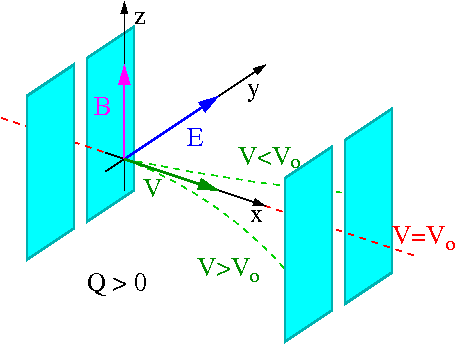
Pole elektryczne
Dane jest stałe jednorodne pole elektryczne
- [math]\vec{E} = ( 0, E, 0)[/math]
Przyjmijmy, że w chwili [math]t_0 = 0[/math] w punkcie [math]\vec{r}_0= (0,0,0)[/math] w pole wlatuje z prędkością [math]\vec{v_0}=(v_0,0,0)[/math] (prostopadłą do kierunku pola!) cząstka o masie [math]m[/math] i ładunku [math]Q[/math].
Wiemy, że siła działająca na tą cząstkę dana jest wzorem:
- [math]\vec{F}_E \; = \; Q \; \vec{E}[/math]
Możemy napisać równania ruchu, odpowiednio dla ruchu wzdłuż osi X i Y:
- [math] m \; \frac{d^2x}{dt^2} \; = \; 0 [/math]
- [math] m \; \frac{d^2y}{dt^2} \; = \; Q \; E [/math]
Całkując powyższe równania po czasie i uwzględniając warunki początkowe otrzymujemy rozwiązania w postaci:
- [math] x(t) \; = \; v_0 \cdot t [/math]
- [math] y(t) \; = \; \frac{Q \; E}{2 m} \cdot t^2 [/math]
Eliminując czas uzyskujemy równanie toru lotu cząstki w postaci:
- [math]y = \frac{Q \; E}{2 m v_0^2 } \cdot x^2 [/math]
W obszarze jednorodnego pola elektrycznego cząstka porusza się po paraboli. Możemy policzyć kąt o jaki odchyli się tor cząstki przy przechodzeniu przez obszar pola (o długości [math]L[/math]). Jest on zadany przez pochodną:
- [math] \tan \theta = \left. \frac{dy}{dx} \right|_{x=L} \; = \; \frac{Q \; E \; L }{m \;v_0^2} [/math]
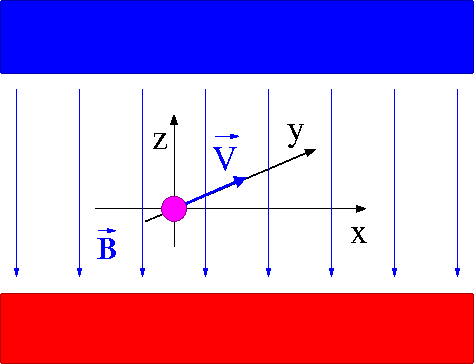
Pole magnetyczne
Rozważmy teraz obszar stałego jednorodnego pola magnetycznego o indukcji
- [math]\vec{B} = ( 0, 0, B)[/math]
W chwili [math]t_0 = 0[/math] w punkcie [math]\vec{r}_0= (0,0,0)[/math] w pole wlatuje z prędkością [math]\vec{v_0}=(0, v_0,0)[/math] cząstka o masie [math]m[/math] i ładunku [math]Q[/math].
Siła działająca na cząstkę naładowaną w polu magnetycznym (siła Lorentza) dana jest wyrażeniem:
- [math]\vec{F}_B \; = \; Q \cdot \vec{v} \times \vec{B}[/math]
Korzystając z definicji iloczynu wektorowego (zapis macierzowy) oraz wyrażając prędkość i siłę przez pochodne położenia otrzymujemy
- [math] m \; \frac{d^2\vec{r}}{dt^2} \; = \; Q \cdot \left( \begin{array}{ccc} \vec{i}_x & \vec{i}_y & \vec{i}_z \\[3mm] \frac{dx}{dt} & \frac{dy}{dt} & \frac{dz}{dt} \\[3mm] 0 & 0 & B \end{array} \right)[/math]
Wzdłuż osi Z siła nie działa, nie ma też prędkości początkowej, ciało pozostanie więc w spoczynku:
- [math]z(t)\;=\;0[/math]
Dla pozostałych składowych otrzymujemy układ dwóch równań:
- [math] m \; \frac{d^2 x}{dt^2} \; = \; ~~~Q\; B \; \frac{dy}{dt} [/math]
- [math] m \; \frac{d^2 y}{dt^2} \; = \; - Q\; B \; \frac{dx}{dt} [/math]
Całkując pierwsze równanie po czasie otrzymujemy
- [math] m \; \frac{d x}{dt} \; = \; Q\; B \; (y - y_c) [/math]
gdzie [math]y_c[/math] jest stałą całkowania.
Wstawiając otrzymane wyrażenie na [math]\frac{d x}{dt}[/math] do drugiego równiania otrzymujemy:
- [math] \frac{d^2 y}{dt^2} \; = \; - \left(\frac{Q\; B}{m}\right)^2 \; (y - y_c)[/math]
Wprowadzając parametr [math]\omega = \frac{Q\;B}{m}[/math]
możemy zapisać otrzymane równania ruchu w postaci:
- [math] \frac{d^2 y}{dt^2} \; = \; - \omega^2 \; (y - y_c) [/math]
- [math] \frac{d x}{dt} \; = \; \omega \; (y - y_c) [/math]
Pierwsze z tych równań jest znanym nam już równaniem oscylatora harmonicznego. Jego rozwiącaniem jest ruch harmoniczny. Drugie równanie wiąże ze sobą ruch w kierunku X i Y. Ogólne rozwiązanie tego układu równań jest postaci:
- [math] x \; = \; r \cdot \sin (\omega t + \phi_0) + x_c [/math]
- [math] y \; = \; r \cdot \cos (\omega t + \phi_0) + y_c [/math]
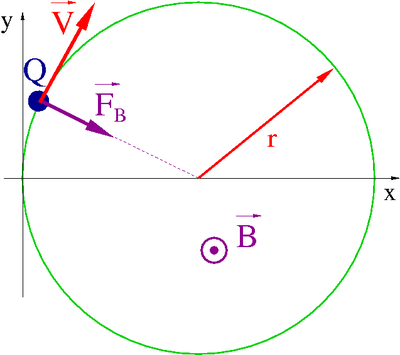
gdzie [math]\omega[/math] nazywamy częstością cyklotronową, a [math]r[/math] - promieniem cyklotronowym:
- [math] r \; = \; \frac{m \; v_0}{Q\; B} [/math]
Ruch w polu magnetycznym
Cząstka poruszać się będzie po okręgu
Uwzględniając podane powyżej warunki początkowe ([math]\vec{r}(0)=\vec{r}_0[/math] i [math]\vec{v}(0)=\vec{v}_0[/math]) możemy wyznaczyć stałe całkowania [math]y_c[/math] i [math]\phi_0[/math]. Otrzymujemy ostateczne rozwiązanie naszego problemu w postaci:
- [math] x \; = \; r \cdot ( 1 - \cos \omega t) [/math]
- [math] y \; = \; r \cdot \sin \omega t [/math]
Ruch w polu magnetycznym jest jednostajny: [math]v=const[/math].
Promień cyklotronowy często wygodnie jest wyrazić przez pęd cząstki:
- [math] r \; = \; \frac{m \; v}{Q\; B} \; = \; \frac{p}{Q\; B}[/math]
(wyrażenie to pozostaje słuszne także w przypadku relatywistycznym!)
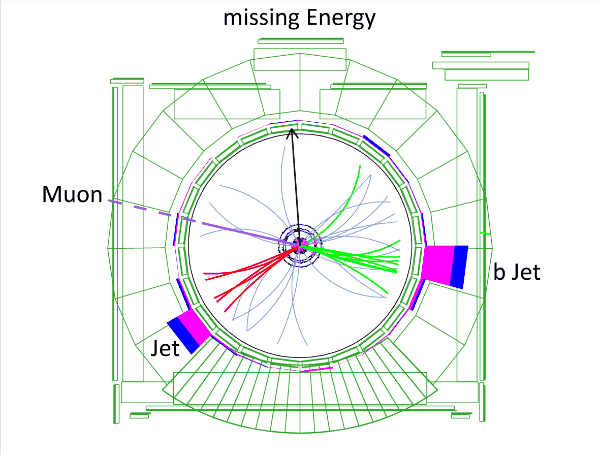
W fizyce cząstek pole magnetyczne
powszechnie wykorzystywane
jest do pomiaru pędu cząstek. Wszystkie
długożyciowe cząstki naładowane mają ładunek [math]\pm 1 e[/math]...
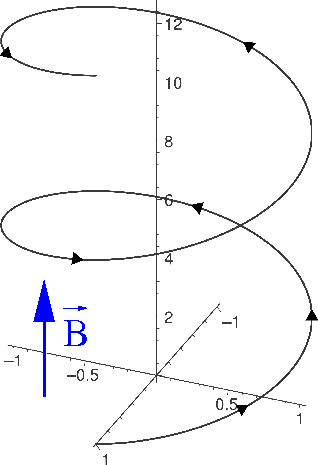
W ogólnym przypadku prędkość cząstki [math]\vec{V}[/math] nie musi być prostopadła do wektora indukcji pola magnetycznego [math]\vec{B}[/math]. Jednak siła Lorenza jest zawsze prostopadła do [math]\vec{B}[/math] ⇒ na kierunku równoległym do pola znika!
W kierunku wektora pola ruch cząstki jest zawsze ruchem jednostajnym. Ruch ten jest niezależny od ruchu po okręgu w płaszczyźnie prostopadłej do pola. W ogólnym przypadku torem ruchu jest więc spirala:
Odchylenie toru
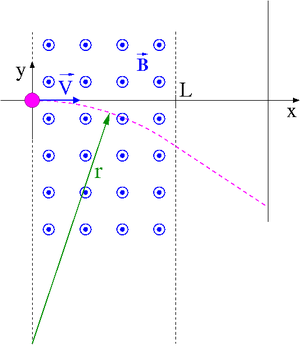
Rozważmy cząstkę przelatującą przez wąski obszar jednorodnego pola magnetycznego
Przyjmijmy przy tym, że promień krzywizny toru jest znacznie większy od obszaru pola w związku z czym odchylenie cząstki od toru prostoliniowego jest małe. Cząstka przebędzie znikomą część łuku okręgu (po którym poruszałaby się, gdyby obszar pola nie był ograniczony), co można zapisać jako warunek [math]\omega t \ll 1[/math].
Możemy w tej sytuacji skorzystać z przybliżonych wzorów
- [math] \sin \omega t \; \approx \; \omega t [/math]
- [math] \cos \omega t \; \approx \; 1 - \frac{(\omega t)^{2}}{2} [/math]
Otrzymane wcześniej rozwiązania równań ruchu sprowadzają sie w tym przybliżeniu do:
- [math] x \; \approx \; r \cdot \omega t [/math]
- [math] y \; \approx \; r \cdot \left[ \left(1 - \frac{(\omega t)^2}{2}\right) \; - \; 1\right] [/math]
Eliminując czas otrzymujemy wyrażenie na tor ruchu:
- [math] y \; \approx \; - \; \frac{x^2}{2\;r}[/math]
Kąt odchylenia cząstki przechodzącej obszar pola o szerokości [math]L[/math] wynosi:
- [math] \tan \theta = \left| \frac{dy}{dx} \right|_{x=L} \; = \; \frac{L}{r} = \frac{Q \; B \; L }{m \;v_0} [/math]
Spektroskop Thomsona
(1913)
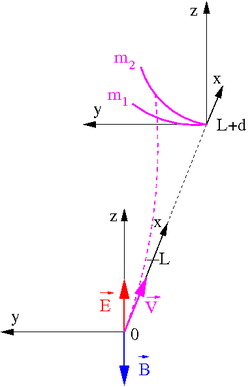
Rozważmy teraz cząstki, które przelatują przez obszar jednorodnych pól [math]\vec{E}[/math] i [math]\vec{B}[/math]
- [math]\vec{E} \; \uparrow \! \downarrow \; \vec{B}[/math]
Obszar, w którym na cząstkę działają siły elektrostatyczna i Lorentza ograniczony jest do [math] 0 \lt x \lt L [/math]. W odległości [math]d[/math] od obszaru pola znajduje się ekran, na którym rejetrowana jest pozycja dolatujących cząstek. Przyjmujemy, że odległość od ekranu jest znacznie większa od szerokości obszaru pola: [math]d \gg L[/math].
Pozycja cząstki na ekranie, czyli dla [math] x_e = L + d [/math] (korzystając z uzyskanych poprzednio wyników dla pola elektrycznego i magnetycznego):
- [math] y_e \; \approx \; d \cdot \tan \theta_B = \frac{Q \; B \; L \; d}{m \;v_0}[/math]
- [math] z_e \; \approx \; d \cdot \tan \theta_E = \frac{Q \; E \; L \; d}{m \;v_0^2} [/math]
Z pierwszej zależności możemy wyznaczyć [math]v_0[/math] i podstawić do drugiego równania. Otrzymamy wzór pozycję śladu cząstek na ekranie: [math] z_e \; = \; \frac{m}{Q} \cdot \frac{ E}{B^2 \; L \; d} \cdot y_e^2[/math]
Cząstki o różnych [math]v_0[/math]
układają się na parabolach odpowiadających
ich [math]\frac{m}{Q}[/math]
⇒ separacja izotopów o różnych masach -
spektroskopia masowa
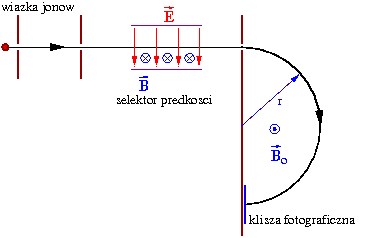
Selektor prędkości
Rozważmy ponownie cząstki, które przelatują przez obszar jednorodnych pól [math]\vec{E}[/math] i [math]\vec{B}[/math], tym razem jednak pola te są prostopadłe do siebie (i prostopadłe do początkowej prędkości cząstki):
- [math]\vec{E} \; \perp \; \vec{B}[/math]
Na cząstkę działają siły elektrostatyczna i Lorentza:
- [math] \vec{F}_E \; = \; Q \cdot \vec{E} [/math]
- [math] \vec{F}_B \; = \; Q \cdot \vec{v} \times \vec{B} [/math]
Obie siły działają wzdłuż tego samego kierunku, lecz mają przeciwne zwroty (zakładając [math]Q\gt 0[/math] i kierunki pól jak na rysunku). Możemy zauważyć, że dla prędkości
- [math]V_0 = \frac{E}{B}[/math]
siły te równoważą się, wypadkowa sił
- [math]\vec{F}_E + \vec{F}_B = 0[/math]
⇒ tor cząstki będzie prostoliniowy
Zastosowanie omówionej kombinacji pól [math]\vec{E}[/math] i [math]\vec{B}[/math] oraz odpowiednich przesłon pozwala na selekcję cząstek o ustalonej prędkości niezależnie od ich ładunku [math]Q[/math] i masy [math]m[/math].
Spektrometr Bainbridge'a
Cząstki o określonej prędkości możemy skierować w obszar jednorodnego pola magnetycznego:
Mierzymy promień toru cząstki w polu magnetycznym, czyli promień cyklotronowy
- [math]r = \frac{m \; v_0}{Q\; B_0}[/math]
Dla cząstek o ustalonej prędkości [math]v_0 = \frac{E}{B}[/math] pozwala to na pomiar stosunku masy do ładunku cząstki
- [math]\frac{m}{Q} \; = \; \frac{r B_0}{v_0} \; = \; \frac{r B_0 B }{E}[/math]
Cząstki o różnych masach zaczernią kliszę w różnych odległościach od szczeliny ⇒ możliwość separacji
Ruch po okręgu
Zasada bezwładności
Zgodnie z pierwaszą zasadą dynamiki sformułowaną przez Newtona:
"Każde ciało trwa w swym stanie spoczynku lub ruchu prostoliniowego i jednostajnego, jeśli siły przyłożone nie zmuszajż ciała do zmiany tego stanu."
Aby więc ciało pozostawało w ruchu po okręgu konieczne jest działanie siły!
⇒siła dośrodkowa
Ruch po okręgu może być wynikiem działania różnego rodzaju sił.
Mogą to być
- siły zewnętrzne
- siła Lorenza (pole magnetyczne)
- siły sprężystości
- siły reakcji więzów (kulka na nitce)
- wypadkowej sił reakcji i sił zewnętrznych (regulator Watta, kulka w wirującym naczyniu...)
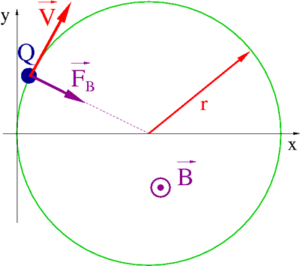
Siła dośrodkowa
Rozważmy dla ustalenia uwagi cząstkę naładowaną poruszającą się w jednorodnym polu magnetycznym prostopadłym do kierunku prędkości [math]\vec{B} \perp \vec{v}[/math] . Promień toru cząstki (promień cyklotronowy) dany jest wzorem:
- [math] r \; = \; \frac{m \; v}{Q\; B} \; = \; \frac{p}{Q\; B} [/math]
Siła Lorentza działająca na cząstke
- [math]\vec{F}_B \; = \; Q \cdot \vec{v} \times \vec{B}[/math]
dla cząstki poruszającej się prostopadle do lini pola ([math]\vec{v} \perp \vec{B}[/math]) ma wartość:
- [math]F_B \; = \; Q \; v \; B [/math]
Przekształcając wyrażenie na siłę możemy powiązać jej wartość z promieniem toru
- [math]\Rightarrow \qquad F_B \; = \; \frac{Q \; B}{m \; v} \; m \; v^2 \; = \; \frac{1}{r}\; m \; v^2 [/math]
Ostatecznie otrzymujemy
| [math] \displaystyle F \; = \; \frac{m \; v^2}{r} \; = \; m \; \omega^2 \; r[/math] |
Jet to ogólne wyrażenie na wartość siły dośrodkowej w ruch jednostajnym po okręgu.
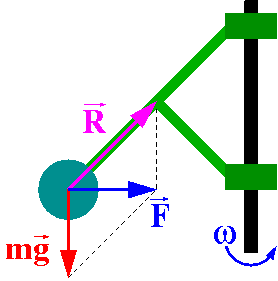
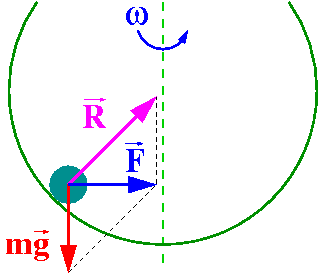
W poniższych dwóch przykładach siła dośrodkowa jest wypadkową
siły reakcji i siły ciężkości.
| [math]\vec{F} \; = \; m \vec{g} \; + \; \vec{R}[/math] |
 |
| |||||
| Regulator Watta | Kulka w wirującym naczyniu |
Przyspieszenie dośrodkowe
Uzyskane wyrażenie na siłę dośrodkową odpowiada (wspomnianemu już wcześniej) przyspieszeniu dośrodkowemu. Dla ruchu jednostajnego po okręgu:
- [math] x \; = \; r \cdot \cos ( \omega \cdot t ) [/math]
- [math] y \; = \; r \cdot \sin ( \omega \cdot t ) [/math]
- [math] z \; \equiv \; 0 [/math]
składowe przyspieszenia (metodą dwukrotnego różniczkowania) wynoszą
- [math] a_x \; = \; - \omega^2 \; r \cdot \cos ( \omega \cdot t ) [/math]
- [math] a_y \; = \; - \omega^2 \; r \cdot \sin ( \omega \cdot t ) [/math]
- [math] a_z \; = \; 0 [/math]
Tym samym spełniona jest zależność:
- [math] \vec{a} \; = \; - \omega^2 \; \vec{r} [/math]
- [math] \vec{F} \; = \; - m \; \omega^2 \; \vec{r}[/math]
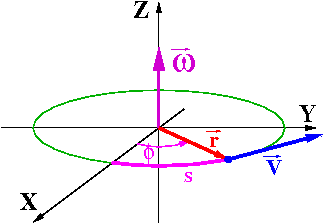
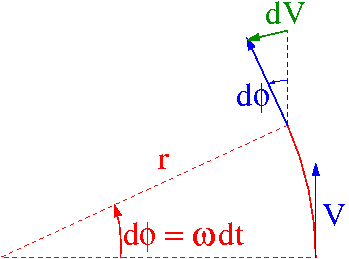
Wyrażenie na wartość przyspieszenia dośrodkowego w ruchu jednostajnym po okręgu można też wyprowadzić wiążąc zmianę wektora prędkości z przesunięciem kątowym:
- [math] dv \; = \; v \cdot d\phi \; = \; v \; \omega \; dt [/math]
- [math] a\; = \; \frac{dv}{dt} \; = \; v \; \omega \; = \; \omega^2 \; r \; = \; \frac{v^2}{r}[/math]
W zapisie wektorowym (przyjmyjąc [math]\vec{\omega} = const[/math])
- [math] \vec{a} \;\; = \;\; \frac{d\vec{V}}{dt} \; = \;
\frac{d(\vec{\omega}\times \vec{r})}{dt}\;\; = \;\;
\vec{\omega} \times \frac{d\vec{r}}{dt} [/math]
- [math] = \; \vec{\omega} \times \vec{V} \;\; = \;\; \vec{\omega} \times ( \vec{\omega} \times \vec{r}) [/math]
- [math] = \; - \omega^2 \cdot \vec{r}_{\perp} [/math]
gdzie [math] \vec{r}_{\perp}=(x,y,0) [/math] jest położeniem w płaszczyźnie prostopadłej do kierunku pola.
Przykład
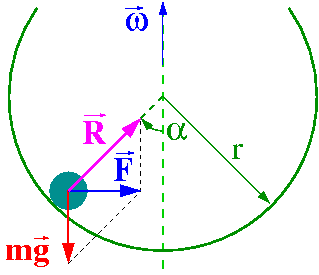
Rozważmy ponownie kulkę w wirującym naczyniu. Pozostaje ona w ruchu po okręgu pod wpływam działania siły ciężkości oraz siły reakcji
- [math]\vec{F} \; = \; m \vec{g} \; + \; \vec{R}[/math]
Siła dośrodkowa musi być skierowana poziomo (prostopadle do osi obrotu), zatem ze składania sił na kierunku pionowym mamy:
- [math] R \cdot \cos \alpha \; - \; m g \; = \; 0 [/math]
i możemy siłę dośrodkową powiązać z kątem wychylenia kulki:
- [math] F \; = \; R \cdot \sin \alpha \; = \; m g \cdot \tan \alpha [/math]
Z równania ruchu:
- [math] F \; = \; m \; \omega^2 r_{\perp} \; = \; m\; \omega^2 r \cdot \sin \alpha [/math]
Przyrównując obie zależności otrzymujemy zależność kąta wychylenia od prędkości wirowania naczynia:
- [math]\cos \alpha \; = \; \frac{g}{ \omega^2 \; r} [/math]
To proste wyrażenie ma głęboki sens fizyczny. Wiemy, że [math]\cos \alpha \le 1 [/math]. Dla małych prędkości wirowania naczynia kulka będzie spoczywała na jego dnie, dokładnie na osi obrotu! Odchyli się dopiero dla
- [math]\omega \gt \sqrt{\frac{g}{r}} = \omega_\circ[/math]
gdzie [math]\omega_\circ[/math] odpowiada częstość drgań wahadła matematycznego o długości [math]r[/math]
Siła sprężysta
W wielu zagadnieniach spotykamy się z siłami będącymi wynikiem odkształcenia ciał. Wyróżniamy wsród nich ciala sprężyste, dla których spełnione jest
Prawo Hooke'a
Prawo Hooke'a jest prawem empirycznym - opartym o wyniki doświadczeń.
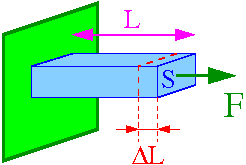
Opisuje ono zależność siły sprężystej [math]F[/math] od
odkształcenia [math]\Delta L[/math] ciała (patrz rysunek):
- [math] F \; = \; E \; S \; \frac{\Delta L}{L} [/math]
gdzie parametr [math]E[/math] jest nazywany modułem Younga (wymiar [[math]N/m^2[/math]])
Moduł Younga formalnie odpowiada naprężeniu, które powodowałoby dwukrotnemu wydłużenie ciała. Jednak prawo Hooka słuszne tylko dla małych naprężeń, nie większych niż około [math]10^{-3} \cdot E[/math]
Dla przykładu, dla miedzi moduł Younga wynosi
- [math]E_{Cu}=1.2\cdot 10^{11}\; \frac{N}{m^2}[/math]
zaś zakres stosowalności prawa Hooka ograniczony jest do naprężeń poniżej (granica proporcjonalności)
- [math]Pr_{Cu}=1.9\cdot 10^{8}\; \frac{N}{m^2}[/math]
Powyżej granicy proporcjonalności dochodzi do trwałego odkształcenia ciał. Przyłożenie dużej siły, nawet na krótki czas może powodować, że ciało nie wróci (po ustaniu działania siły) do początkowych rozmiarów lub kształtu. Potrzebne w tym celu przyłożenie przeciwnie skierowanej siły. Rozmiary lub kształt ciała zaczynaja zależeć nie tylko od aktualnie przyłożonej siły, ale także od "historii" ich działania (zjawisko histerezy).
Należy też pamiętać, że prawo Hooke'a odnosi się do sytuacji statycznej. Od momentu przyłożenia siły do osiągnięcia odpowiedniego odkształcenie mija skończony czas - czas relaksacji, podobnie gdy siła przestanie działać. Mogą to być czasy makroskopowe (rzędu minut).
Przy dalszym zwiąkszaniu naprężenia powyżej granicy proporcjonalności
może nastąpić rozerwanie materiału (tzw. granica wytrzymałości).
Tarcie
Tarcie kinetyczne
Tarcie kinetyczne jest to siła pojawiająca się między dwoma
powierzchniami poruszającymi się względem siebie,
dociskanymi siłą N.
Ścisły opis sił tarcia jest bardzo skomplikowany.
Jednak w większości zagadnień, w których mamy z nimi do czynienia
możemy stosować prawo empiryczne:
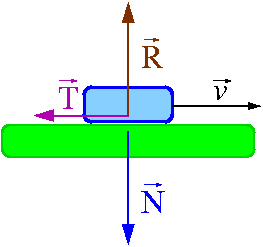
- [math] \vec{T} \; = \; - \mu_k \; \vec{i}_v \; N[/math]
gdzie [math]\mu_k[/math] jest tzw. współczynnikiem tarcia kinetycznego a [math]\vec{i}_v = \frac{\vec{v}}{v}[/math] jest wektorem jednostkowym zgodnym z kierunkiem ruchu ciała.
Ze związku tego wynika, że siła tarcia kinetycznego:
- jest proporcjonalna do siły dociskającej (składowej prostopadłej do powierzchni)
- nie zależy od powierzchni zetknięcia
- nie zależy od prędkości
Należy jednak pamiętać, że jest to prawo empiryczne, a więc przybliżone !!!
Obraz mikroskopowy
Tarcie wywołane jest przez oddziaływanie elektromagnetyczne cząstek stykających się ciał. Powierzchnie ciał nigdy nie są idealnie równe: na poziomie mikroskopowym cząstki jednego ciała "blokują drogę" cząstkom drugiego ciała ⇒ muszą zostać "odepchnięte". Wymaga to przyłożenia siły.
Zależność od nacisku wynika z faktu, że powierzchnia rzeczywistego (mikroskopowego) styku dwóch ciał jest w normalnych warunkach wiele rzędów wielkości mniejsza niż ich powierzchnia geometryczna. Ilustruje to poniższa tabela (przykładowo dla dwóch wypolerowanych płyt stalowych):
| siła dociskająca | ułamek powierzchni |
|---|---|
| 1 N/cm[math]^2[/math] | 0.00001 |
| 2.5 N/cm[math]^2[/math] | 0.000025 |
| 50 N/cm[math]^2[/math] | 0.0005 |
| 250 N/cm[math]^2[/math] | 0.0025 |
Efektywna powierzchnia styku dwóch ciał jest w szerokim zakresie proporcjonalna do nacisku. Oznacza to, że liczba oddziaływań na poziomie atomowym, które są źródłem siły tarcia, też jest proporcjonalna do nacisku.
Odstępstwa od praw empirycznych
Na poziomie mikroskopowym tarcie prowadzi trwałych zmian w stykających się powierzchniach. W szczególności może następować ich ścieranie.
Przy dużych siłach dociskających mogą się pojawić odstępstwa od zależnosci liniowej wynikające np. ze zmiany struktury powierzchni (np. zniszczenie warstwy tlenków na powierzchni miedzi).
Odstępstwa mogą się też pojawić przy dużych prędkościach, np. związane ze zwiększaniem temperatury ciał w miejscu styku.
Smarowanie
Tarcie zmniejszamy wprowadzając smar
między poruszające
się powierzchnie.
Smar bardzo dobrze "zwilża" (pokrywa) powierzchnie ciał, tak że na poziomie mikroskopowym nie stykają się. W ten sposób możemy praktycznie wyeliminować tarcie, pojawia się jednak nowa siła oporu związana z lepkością...
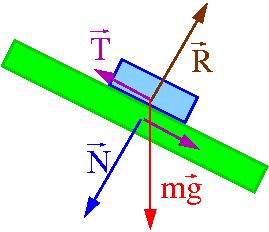
Tarcie statyczne
Ciało na które działają siły zwnętrzne (np. siła ciężkości w przypadku klocka leżącego na równi pochyłej) może pozostawać w równowadze dzięki działaniu tarcia statycznego.
Tarcie statyczne jest to siła działająca między dwoma powierzchniami nieruchomymi względem siebie, dociskanymi siłą N.
Wartość siły tarcia statycznego jest każdorazowo określona przez warunek równowagi sił!
Od siły dociskającej oraz rodzaju powierzchni zależy jednak maksymalna siła tarcia statycznego [math]T_S^{max}[/math]. Jest ona równa najmniejszej sile [math]F[/math] jaką należy przyłożyć do ciała, aby ruszyć je z miejsca.
Prawo empiryczne mówi nam, że:
- [math] \vec{T}_S^{max} \; = \; - \mu_s \; \vec{i}_F \; N [/math]
gdzie wektor jednostkowy [math] \vec{i}_F = \frac{\vec{F}}{F} [/math] określa kierunek działania wypadkowej siły zewnętrznej (równoległy do powierzchni styku).
Póki przyłożona siła [math]\vec{F}[/math] jest mała, tarcie statyczne
utrzymuje ciało w spoczynku:
- [math]\vec{T}_s \; = \; - \vec{F} [/math]
⇒ siła tarcia rośnie proporcjonalnie do przyłożonej siły.
Gdy przyłożona siła przekroczy wartość [math]T_S^{max} = \mu_s \cdot N [/math] ciało zaczyna się poruszać i w miejsce tarcia statycznego pojawia się tarcie kinetyczne.
Tarcie kinetyczne naogół słabsze od spoczynkowego:
- [math]\mu_k \lt \mu_s[/math]
Przykładowe współczynniki dla wybranych materiałów:
| materiały | [math]\mu_s[/math] | [math]\mu_k[/math] |
|---|---|---|
| stal o stal | 0,15 | 0,03-0,09 |
| stal o lód | 0.027 | 0.014 |
| drewno o drewno | 0,65 | 0,2-0,4 |
| guma o beton suchy | 1,0 | 0,7 |
| guma o beton mokry | 0,7 | 0,5 |
Dlatego właśnie (tarcie gumy o beton) w przypadku hamowanie samochodu ważne jest aby koła nie zaczęły się ślizgać:
- poślizg ⇒ [math]T \sim \mu_k[/math]
- dobry kierowca lub ABS ⇒ [math]T \sim \mu_s[/math]
Brak poślizgu może oznaczać "zysk" [math]\sim[/math]40% na drodze hamowania...
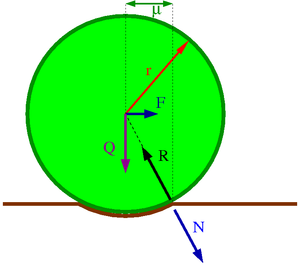
Tarcie toczne
Toczące się ciało odkształca zawsze powierzchnię po której się toczy (nawet jeśli są to tylko odkształcenia na poziomie mikroskopowym).
Dlatego poza tarciem statycznym i kinetycznym (poślizgowym) wyróżniamy też tarcie toczne. W tym przypadku empiryczna formuła na siłę tarcia zależy dodatkowo od promienia toczącego się ciała [math]r[/math]:
- [math] \vec{T}_t \; = \; - \mu_t \; \vec{i}_F \; \frac{N}{r} [/math]
Współczynnik tarcia tocznego [math]\mu_t[/math]
jest zwykle bardzo mały. Przykładowo:
- drewno + drewno ⇒ [math]\mu_t[/math]= 0,0005 m
- stal hartowana + stal ⇒ [math]\mu_t[/math]= 0,00001 m
Współczynnik tarcia tocznego ma wymiar długości! Odpowiada formalnie promieniowi kulki przy toczeniu której siła tarcia byłaby równa sile nacisku.
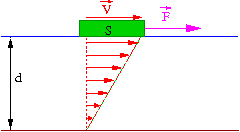
Lepkość
Jak już zostało wspomniane powyżej, jeśli pomiędzy dwoma ciałami znajduje się ciecz (np. smar) to mamy do czynienia z siłami lepkości.
Z analogiczną sytuacją mamy do czynienia, gdy ciało poruszające się po powierzchni cieczy (np. łódka na jeziorze). Drugim ciałem jest wtedy dno (ew. ścianki) zbiornika lub naczynia.
Warstwa cieczy bezpośrednio przylegająca do ciała porusza się wraz z nim.
Z kolei warstwa cieczy przylegająca do dna spoczywa.
Zmiany prędkości poruszania się cieczy nie mogą następować skokowo,
pomiędzy dnem a poruszającym się ciałem kolejne warstwy cieczy poruszają
się z różnymi prędkościami ⇒ powoduje to powstanie
"tarcia wewnętrznego" pomiędzy warstwami cieczy.
Formuła empiryczna:
- [math] \vec{F}_L \; = \; - \vec{i}_V \; \eta \;\frac{v\; S}{d} [/math]
| gdzie: | [math]v[/math] - prędkość ciała |
| [math]S[/math] - powierzchnia styku z cieczą | |
| [math]d[/math] - głębokość naczynia | |
| [math]\eta[/math] - współczynnik lepkości |
Pojęcie lepkości możemy stosować także w przypadku gazów (w przypadku cienkich warstw).
Typowe wartości współczynnika lepkości:
| gaz/ciecz | [math]\eta \; \; [Ns/m^2][/math] |
|---|---|
| wodór | 0,000009 |
| powietrze | 0,000018 |
| tlen | 0,000021 |
| eter | 0,0002 |
| woda | 0,001 |
| gliceryna | 1,5 |
| miód | 500 |
Lepkość cieczy maleje z temperaturą, zaś lepkość gazów rośnie z temperaturą.
Ruch w ośrodku
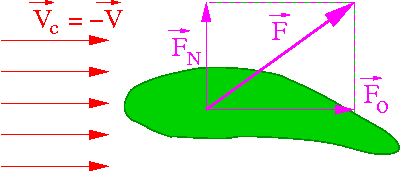
Siły jakie działają na ciało poruszające się w ośrodku możemy ogólnie podzielić na:
- siłę oporu czołowego [math]\vec{F}_\circ \; \uparrow \! \downarrow \vec{v}[/math]
- siłę nośną [math]\vec{F}_N \; \perp \vec{v}[/math]
Obie te siły zależą od kształtu (także orientacji) i rozmiarów ciała, jego prędkości względem ośrodka, oraz parametrów tego ośrodka.
Opór czołowy
W przypadku oporu czołowego możemy posłużyć się analizą wymiarową. Siła oporu musi wyrażać się wzorem (wzór Newtona):
- [math] \vec{F}_\circ \; = \; -\vec{i}_v \; \frac{ C}{2} \rho v^2 S [/math]
| gdzie: | [math]v[/math] - prędkość ciała |
| [math]S[/math] - powierzchnia poprzeczna | |
| [math]\rho[/math] - gęstość cieczy |
Oprócz tych trzech wielkości siła może zależeć jedynie od bezwymiarowego współczynnika [math]C[/math]. Współczynnik ten zależy od kształtu ciała, jego orientacji w ośrodku (względem kierunku [math]\vec{v}[/math]) oraz bezwymiarowej kombinacji innych parametrów, zwanej liczba Reynoldsa:
- [math] Re \; = \; \frac{v \;l \;\rho }{\eta}[/math]
gdzie: [math]l[/math] - wymiar poprzeczny ciała
Dla ciała kulistego i [math]Re \ll 1[/math] (granica małych prędkości) istnieje ścisłe rozwiązanie problemu (G.Stokes 1851):
- [math] C \; = \; \frac{24}{Re} [/math]
- [math] \vec{F}_\circ \; = \; -6 \pi \eta r \; \vec{v} [/math]
Dla odpowiednio małych prędkości (także w przypadku innych ciał) siła oporu czołowego będąca wynikiem działania sił lepkości jest proporcjonalna do prędkości ciała [math]v[/math].
Z kolei w obszarze dużych wartości [math]Re[/math], [math]Re \gg 1[/math] (w przypadku kuli począwszy od [math]Re \sim 10^{3}[/math] uzyskane wyniki doświadczalne wskazują na stałą wartość parametr [math]C[/math], [math] C \; \approx \; const[/math]. Oznacza to, że w granicy dużych prędkości siła oporu czołowego rośnie z kwadratem prędkości
- [math] F_\circ \; \sim \; v^2 [/math]
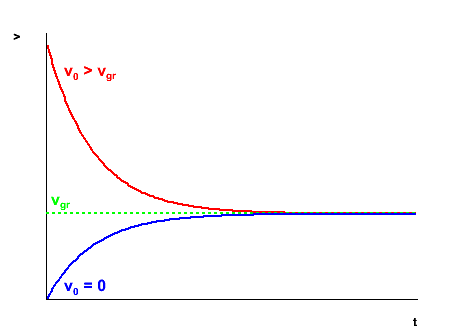
Prędkość graniczna
Rozważmy kulę spadającej swobodnie w cieczy. Działa na nią siła ciężkości, siła wyporu oraz siła oporu czołowego. Równanie ruchu kuli, w granicy małych prędkości ([math]Re \ll 1[/math]) można zapisać jako:
- [math] m \vec{a} \; = \; m \vec{g} \; - \; m_p \vec{g} - 6\pi \eta r \vec{v} [/math]
Rozwiązanie jest postaci (ruch w pionie):
- [math] v(t) \; = \; v_{gr} \; + \; (v_0 - v_{gr})\exp \left( - \frac{6\pi \eta r}{m} \; t \right) [/math]
gdzie: [math]v_{gr}[/math] - prędkość graniczna
Zależnie od tego, czy na początku prędkość kuli była mniejsza (np. spadek swobodny) czy większa (np. strzał z karabinu) od prędkości granicznej, prędkość ciała będzie rosła lub malała dążąc (formalnie dla [math]t \rightarrow \infty [/math]) do wartości [math]v_{gr}[/math].
Dla kuli spadającej w cieczy
(w granicy małych prędkości [math]Re \ll 1[/math])
- [math] v_{gr} \; = \; \frac{2}{9} \; \frac{r^2 g (\rho - \rho_p)}{\eta} [/math]
Prawo Bernouliego
Lepkość nie jest jedynym źródłem sił działających na ciało w ośrodku.
Prawo Bernouliego wiąże wysokość [math]h[/math] (w polu grawitacyjnym Ziemi)
i prędkość [math]v[/math] przepływu cieczy z ciśnieniem cieczy [math]p[/math]:
- [math]\displaystyle \rho g h + \frac{\rho v^2}{2} + p = const[/math]
Ciśnienie (nacisk na jednostkę powierzchni) jakie ciecz wywiera na ciało jest mniejsze w obszarze wiekszych prędkości opływania. Różnica ciśnień działających na różne powierzchnie ciała (np. skrzydła samolotu) powoduje powstanie siły nośnej, prostopadłej do kierunku przepływu. Kierunek działania siły jest taki jakby ciało było "wciągane" w obszar wiekszych prędkości.
Ale można na to spojrzeć też z punktu widzenia
praw Newtona!
Obecność "skrzydła" wymusza zmianę kierunku ruch cząsteczek ośrodka, pcha je "w dół".
Z III zasady dynamiki ośrodek musi działać na skrzydło siłą skierowaną ku górze.
Siła nośna jest siłą reakcji!
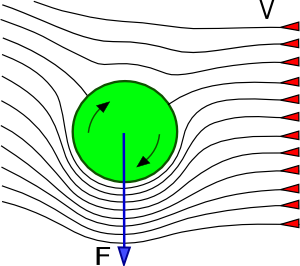
Zjawisko Magnusa
Obserwujemy je w przypadku walca wirującego szybko w przepływającej poprzecznie do osi obrotu cieczy lub gazie.
Rozważny ruch i ciśnienie ośrodka powyżej i poniżej walca.
- poniżej walca: zgodne kierunki prędkości ośrodka i walca
- ⇒ prędkość przepływu wzrasta
- ⇒ przyspieszenie dośrodkowe rośnie
- ⇒ ciśnienie maleje
- powyżej walca: przeciwne kierunki prędkości
- ⇒ prędkość przepływu maleje
- ⇒ przyspieszenie dośrodkowe maleje
- ⇒ ciśnienie wzrasta
W wyniku różnicy prędkości opływania walca przez ośrodek powstaje wypadkowa siła nośna [math]\vec{F}_N \perp \vec{v}[/math]