FizykaI FMiN/STW: Różnice pomiędzy wersjami
(Utworzono nową stronę " <span style="font-size:40px">Szczególna teoria względności</span><br><br> ==Zdarzenia i czasoprzestrzeń== ===<u>'''Zdarzenia'''</u>=== Doświadczenie to <span st...") |
|||
| Linia 1: | Linia 1: | ||
| − | + | __NOTOC__ | |
<span style="font-size:40px">Szczególna teoria względności</span><br><br> | <span style="font-size:40px">Szczególna teoria względności</span><br><br> | ||
Wersja z 10:13, 24 cze 2015
Szczególna teoria względności
Zdarzenia i czasoprzestrzeń
Zdarzenia
Doświadczenie to (najczęściej) pomiar jakiejś wielkości fizycznej lub (rzadziej) obserwacja jakiegoś zjawiska (np. zmiany stanu skupienia).
Oba przypadki możemy sprowadzić do rejestracji różnego typu zdarzeń.
Przykład: pomiar przyspieszenia spadającego jabłka możemy sprowadzić do rejestracji dwóch zdarzeń
- Zdarzenie A: jabłko odrywa się od gałęzi
- Zdarzenie B: jabłko upada na ziemię
Aby wyznaczyć przyspieszenie jabłka
(zakładając, że ruch jest jednostajnie
przyspieszony) musimy znać zarówno czas
jak i położenie jabłka
dla obu tych zdarzeń.
W Szczególnej Teorii Względności zdarzeniem nazywamy
jednoczesne określenie czasu i położenia. Zdarzenie jest więc
każde zjawisko zachodzące w pewnym miejscu w przestrzeni
i w pewnej chwili czasu.
Przykłady:
- obserwacja (pomiar) położenia jabłka (w danej chwili czasu)
- zderzenie kulek (zaniedbując ich rozmiary)
- rozszczepienie jądra atomowego
- start rakiety
- lądowanie rakiety na Księżycu
- wysłanie lub rejestracja impulsu laserowego, cząstki itp.
| Zdarzenie = Czas + Położenie |
Od pierwszego wykładu zajmowaliśmy się różnego typu zdarzeniami, choć tak tego nie nazywaliśmy. W mechanice klasycznej koncepcja zdarzenia nie jest wykorzystywana, gdyż czas jest pojęciem uniwersalnym. W mechanice relatywistycznej pomiar czasu jest zawsze związany z jakimś punktem w przestrzeni...
Linia świata
Możemy wyróżnić pewne szczególne zbiory zdarzeń.
Wyobraźmy sobie, że obserwujemy jakiś obiekt
(np. UFO) i rejestrujemy
w sposób ciągły zmiany jego położenia w czasie. Mamy ciągłą serię pomiarów
czasu i położenia.
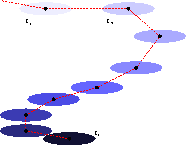
Zbiór zdarzeń opisujących ruch konkretnego ciała
nazywamy "linią świata" tego ciała.
W wymiarach przestrzennych linia świata to po prostu tor.
Znając linię świata wiemy dokładnie jak poruszało się dane ciało.
Oczywiście kształt linii świata zależy od wybranego układu odniesienia.
Transformacja Galileusza
Transformacja ukladu współrzędnych
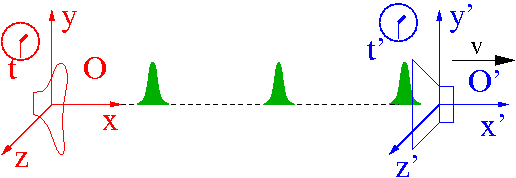
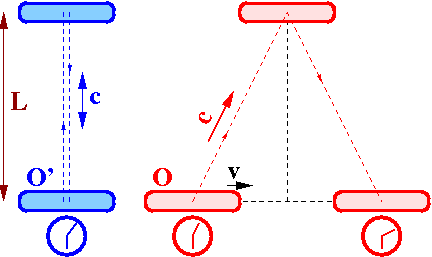
Gdy rozpatrujemy efekt Dopplera zdarzeniem jest zarówno wysłanie każdego impulsu, jak i jego rejestracja.
Oba typy zdarzeń mogą być zmierzone (czas i położenie) przez obu obserwatorów: O' związanego ze źródłem i rejestrującego impulsy O. Dla każdego przekazywanego impulsu mamy więc łącznie 4 pomiary (2 zdarzeń).
W przypadku ogólnym obserwując to samo zdarzenie każdy z obserwatorów może zmierzyć inne współrzędne. Jeśli wiemy jak obserwatorzy poruszają się względem siebie, powinniśmy móc wyznaczyć transformacje
- [math] (t,x,y,z)~~~ \Leftrightarrow~~~ (t',x',y',z')[/math]
Uniwersalność czasu
Uniwersalność czasu była podstawowym założeniem w fizyce klasycznej (Newtonowskiej). Czas nie zależał od układu odniesienia. Współrzędna czasowa danego zdarzenia była taka sama dla dowolnego obserwatora.
Jeśli układ O' poruszał się z prędkością [math]V[/math] w dodatnim kierunku osi X układu O to transformację współrzędnych zdarzeń między tymi układami można zapisać w postaci
- [math] \left\{\begin{array}{rcl} t & = & t' \\ x & = & x' + V \; t' \\ y & = & y' \\ z & = & z' \end{array}\right. [/math]
gdzie zakładamy, że w chwili [math]t=t'=0[/math] początki układów pokrywały się.
Powyższa transformacja nazywana jest Transformacją Galileusza
Konsekwencją założonej uniwersalności czasu jest jednak
względność prędkości.
Każda prędkość, także prędkość światła
zmienia się przy zmianie okładu odniesienia
| [math]v = v' + V[/math] |
Transformacja Galileusza zapewnia niezmienniczość
klasycznych praw ruch (zasad dynamiki Newtona)
przy zmianie układu odniesienia!
Jest zgodna z zasadą względności, którą
Galileusz sformułował w roku 1604:
"Wszystkie układy odniesienia poruszające się względem siebie ze stałą prędkością są równoważne"
Zasada względności nie oznacza wcale, że nie istnieje wyróżniony
układ odniesienia. Obserwacje mikrofalowego
promieniowania tła, pozostałości
Wielkiego Wybuchu, w którym powstał
Wszechświat, pozwalają wskazać związany
z nim układ odniesienia.
Można powiedzieć, że jest to układ własny Wszechświata.
Ale prawa fizyki są w nim takie same jak w każdym innym układzie
inercjalnym!
Prędkość światła
Historia pomiarów
Już Galileusz zastanawiał się nad prędkością rozchodzenia się światła. Jako pierwszy zaproponował pomiar prędkości światła metodą czasu przelotu. Jednak przy ówczesnych dokładnościach pomiarów ([math]\Delta L \sim 1\;m [/math], [math] \Delta t \sim 1 \; s [/math]) było to niewykonalne. Nie w warunkach ziemskich...
W 1676 Ole Rømer zauważył, że obserwowany na Ziemi czas zaćmień satelity Io Jowisza zależy od położenia Ziemi względem Jowisza. Maksymalne opóźnienie czasu zaćmienia wynosi około 16 minut. Rømer przyjął (słusznie), że opóźnienie to wynika ze zmiany odległości Ziemi od Jowisza o długość średnicy orbity Ziemi. Według ówczesnych pomiarów tej orbity oszacował [math]c = 214 000 \; km/s[/math]
W 1727 William Bradley wyznaczyl prędkość światła z aberracji gwiazd. Gwiazdy zmieniają w ciągu roku swoje położenie na sferze niebieskiej o ok. 20.5 sekundy łuku, co jest wywołane przez ruch Ziemi dookoła Słońca (przy skończonej prędkości rozchodzenia się światła). Na tej podstawie wyznaczył [math]c = 301 000 \; km/s[/math]
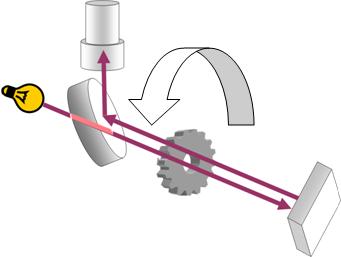
Pierwszy pomiar w warunkach "laboratoryjnych" (ziemskich) został przeprowadzony przez H.L.Fizeau w roku 1849.
Światło było wysyłane na odległość [math]L=8633[/math] m i wracało do obserwatora po odbićiu w zwierciadle. Na początku i na końcu drogi promień przechodził przez przerwę między zębami obracającej się przesłony. Odbity promień przestawał docierań do obserwatora, gdy liczba obrotów przesłony o [math]N=720[/math] zębach wynosiła [math]n=12.86\;s^{-1}[/math]. Na tej podstawie Fizeau oszacował prędkość światła na
- [math]c \approx 315 300[/math] km/s
W kolejnych latach L.Foucault udoskonalił tą metodę używając wirującego
zwierciadła zamiast koła zębatego. Bardzo dokładne pomiary nową metodą
przeprowadził A.Michelson w latach 1924-26. Na odległości
L = 35 km [math]\pm[/math]3 mm (!) między Mt.Wilson i Mt.San Antonio
otrzymal wynik
- c=299 796[math]\pm[/math]4 km/s
W latach 70 XX wieku prędkość światła zmierzono z dokładnością
do około 1 m/s !
Mierzono też prędkości rozchodzenia się fal elektromagnetycznych w innych zakresach częstości (od fal radiowych, [math]\nu \sim 10^7[/math] Hz, do promieniowania [math]\gamma[/math], [math]\nu \sim 10^{24}[/math] Hz). Nie zaobserwowano żadnych różnic w prędkościach rozchodzenia się fal, w granicach błedów pomiarowych.
Dziś już nie mierzymy prędkości światła !
W 1983 roku prędkość światła została zdefiniowana jako
- [math] c\; = \; 299792458\;m/s[/math] (dokładnie !)
wybrana wartość zgodna jest z wcześniejszymi pomiarami. Teraz 1 metr jest zdefiniowany jako odległość jaką pokonuje świato w próżni w czasie równym 1/299792458 sekundy.
Równania Maxwella
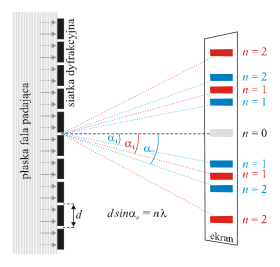
Na początku XX wieku panowało powszechne przekonanie o falowej naturze światła, która przejawiała się m.in. w zjawiskach dyfrakcji i interferencji. Rozchodzenie się światła jako fali elektromagnetycznej opisywały Równania Maxwella (1865):
- [math] \varepsilon_\circ \; div \vec{E} \; = \; \rho [/math]
- [math] rot \vec{E} \; = \; -\mu_\circ \; \frac{\partial \vec{B}}{\partial t} [/math]
- [math] div \vec{B} \; = \; 0 [/math]
- [math] rot \vec{B} \; = \; \vec{j} + \varepsilon_\circ \;\frac{\partial \vec{E}}{\partial t}[/math]
Z równań tych wynikało, że prędkość rozchodzenia się fali elektromagnetycznej wynosi:
- [math] c = \frac{1}{\sqrt{\varepsilon_\circ \mu_\circ }}[/math]
Jednak równania Maxwella nie są niezmiennicze względem
transformacji Galileusza.
W szczególności wynika z nich,
że prędkość światła zależy jedynie od stałych
opisujących oddziaływania magnetyczne i
elektryczne
(prawo Ampera i prawo Coulomba),
a więc jej wartość
nie zależy od układu odniesienia! W każdym układzie powinna być
taka sama!?
Z transformacji Galileusza wynika, że powinna zależeć od układu odniesienia!
Eter
Ale ten sam problem możemy dostrzec w przypadku rozchodzenia siędźwięku. Prędkość rozchodzenia się dźwięku wyraża się przez parametry ośrodka(!). Z definicji jest więc ustalona tylko względem ośrodka (w układzie w którym ośrodek spoczywa). Dzieki temu nie ma sprzeczności opisu propagacji fal dźwiękowych z transformacją Galileusza i jego prawem "dodawania" prędkości.
Podobnie mogłoby być w przypadku światła: jeśli jesteśmy w stanie wskazać ośrodek w którym światło się rozchodzi, to równania Maxwella nie są sprzeczne z transformacją Galileusza.
Poszukiwany ośrodek nazwano eterem...
Doświadczenie Michelsona-Morleya (1887)
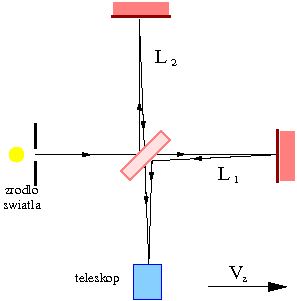
Jednym z doświadczeń, które miało zmierzyć prędkości Ziemi względem eteru było doświadczenie Michelsona-Morleya. W doświadczeniu tym wykorzystywano interferometr, który pozwalał na pomiar zmian w różnicy czasu przelotu światła w dwóch prostopadłych ramionach interferometru.
Jeśli przyjmiemy, że ramię [math]L_1[/math] interferometry
skierowane jest zgodnie z kierunkiem ruchu Ziemi względem eteru
a ramię [math]L_2[/math] prostopadle to
czas przelotu światła w ramionach interferometru wyniesie
- [math] \Delta t_1 \; = \; \frac{L_1}{c+v_Z} + \frac{L_1}{c-v_Z} [/math]
- [math] \; = \; \frac{2 L_1}{c} \cdot \frac{1}{1 - \beta^2} [/math]
- [math] \Delta t_2 \; = \; \frac{2 L_2}{c} \cdot \frac{1}{\sqrt{1 - \beta^2}} [/math]
gdzie [math] \beta = \frac{v}{c} [/math].
Czas propoagacji zależy od kierunek ruchu względem eteru!
Światło z dwóch ramion interferometru interferuje ze sobą. Zmiana różnicy czasu przelotu związana ze zmianą kierunku ruchu względem eteru powodowałaby mierzalne przesunięcia prążków interferencyjnych. Zmianę taką, zakładając że Ziemia porusza się względem eteru, można uzyskać obracając interferometr. Jednak mimo wielokrotnie powtarzanych pomiarów (o różnych porach dnia i różnych porach roku) wynik był zawsze negatywny (brak efektu)!
Wyniki
Negatywny wynik doświadczenia Michelsona-Morleya wskazywał, że Ziemia nie porusza się względem ośrodka, w którym rozchodzi się światło.
Doświadczenia tego typu powtarzano wielokrotnie, także w dłuższych okresach (aby wykorzystać zmianę kierunku prędkości Ziemi w ruchu orbitalnym) zawsze z wynikiem negatywnym.
Wszystkie wyniki wskazywały, że prędkość światła jest stała (względem źródła) i nie zależy od układu odniesienia.
W świetle tych wyników równania Maxwella nie dawały się pogodzić z transformacją Galileusza (postulatem uniwersalności czasu).
Teoria względności Einsteina
Postulaty Einsteina
W roku 1905 Einstein opublikował pracę "O elektrodynamice ciał w ruchu". Zawarł w niej dwa postulaty, które "wystarczają do podania prostej, wolnej od sprzeczności elektrodynamiki ciał w ruchu, opartej na teorii Maxwella...". Te postulaty to:
- prawa fizyki są identyczne w układach będących względem siebie w ruchu jednostajnym prostoliniowym (zasada względności Galileusza)
- prędkość światła w próżni, [math]c[/math], jest jednakowa w każdym kierunku we wszystkich inercjalnych układach odniesienia, niezależnie od wzajemnego ruchu obserwatora i źródła (uniwersalność prędkości światła)
Drugi postulat oznacza odrzucenie transformacji Galileusza na rzecz równań Maxwella.
Okazuje się, że transformacja Galileusza nie jest jedyną transformacją, która zgodna jest z zasadą względności. Jeśli odrzucimy postulat uniwersalności czasu istnieje drugie rozwiązanie, którym jest transformacja Lorentza.
Wzgledność czasu
Uniwersalność prędkości światła nie da się pogodzić z uniwersalnością czasu !
Rozważmy obserwatora O', który porusza się z prędkością [math]v[/math] względem układu O
Obserwator O' odmierza czas przy pomocy zegara świetlnego. Takt zegara odpowiada przejściu błysku światła między dwoma zwierciadłami odległymi o [math]l[/math]. Dla obserwatora O' takt ten wynosi
- [math]\Delta t' = \frac{2 l}{c}[/math]
Dla obserwatora O światło pokonuje dłuższą drogę. Jego zdaniem takt zegara wyniesie
- [math]\Delta t = \frac{2 l}{\sqrt{c^2 - v^2}}[/math]
Okazuje się więc, że dla obserwatora O zegar w O' chodzi wolniej!
Nazywamy to dylatacją czasu:
- [math]\Delta t = \frac{\Delta t'}{{\sqrt{1 - \frac{v^2}{c^2}}}}[/math]
Konstrukcja układu współrzędnych
Z naszych rozważań wynika, że czas w jednym układzie biegnie wolniej niż w drugim. Ale przecież żaden układ nie powinien być wyróżniony !? Musimy bliżej zastanowić się nad konstrukcją układu współrzędnych.
Dla współrzędnych przestrzennych jest to proste: wystarczy, że mamy wzorzec jednostki długości, odkładając ten wzorzec wzdłuż toru ciała swobodnego (lini prostej) otrzymujemy pierwszą oś współrzędnych.
Kolejne osie układu konstruujemy prostopadle do pierwszej. Nie potrzebujemy kątomierza. Wystarczą nam jednakowej długości tyczki lub sznurki, które pozwolą nam na konstrukcję trójkąta równoramiennego. Możemy też skorzystać z twierdzenia Pitagorasa...
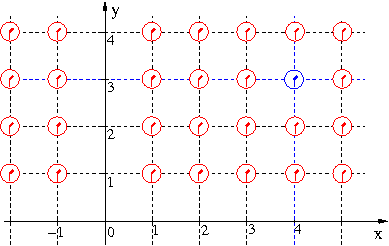
Dodatkowo kreśląc linie równoległe do osi przechodzących przez początek układu otrzymujemy siatkę współrzędnych. Pozycję zdarzenia możemy zawsze zdefiniować poprzez podanie najbliższego węzła siatki.
Pozostaje nam do wybrania "oś czasu".
Czy wystarczy nam jeden zegar w początku układu współrzędnych?
| Nie ! |
Potrzebny jest nam zegar referencyjny
w początku układu współrzędnych, ale do określenia współrzędnej
czasowej zdarzenia potrzebny jest zegar
w każdym węźle siatki.
Inaczej pomiar będzie zależał od metody
odczytu wskazań zegara referencyjnego.
Zegary siatki muszą być oczywiście zsynchronizowane z zegarem referencyjnym. Nie można (jak się później przekonamy) zrobić tego synchronizując zegary w początku układu, a następnie roznosząc je do poszczególnych węzłów siatki - ruch może wpływać na bieg zegarów (wyobraźmy sobie, że mamy zegary wahadłowe).
Synchronizacja zegarów
Synchronizację można przeprowadzić poprzez wysłanie impulsów światła. Przyjmijmy, że o określonej godzinie wysyłamy impuls z wybranego zegara do zegara referencyjnego oraz z zegara referencyjnego do wybranego zegara.
Jeśli oba impulsy dotarły o tej samej godzinie (odczytanej na zegarze do którego dotarł impuls) to oznacza, że zegary są zsynchronizowane. Jeśli nie to połowa różnicy tych czasów daje nam poprawkę dla wybranego zegara.
Aby zastosować tą metodę synchronizacji nie musimy znać prędkości światła. Zakładamy tylko, że nie zależy ona od kierunku rozchodzenia!
Wszystkie zegary rozmieszczone w węzłach skonstruowanej przez nas siatki układu współrzędnych spoczywają w tym układzie.
Można więc powiedzieć, że układ inercjalny to rodzina swobodnych (zsynchronizowanych) zegarów.
Dylatacja czasu
Powróćmy do rozważanego wcześniej pomiaru czasu przy pomocy zegara świetlnego. Dla obserwatora O zegar w początku układu O' chodzi wolniej (niż jego zegar).
Ale układy powinny być równoważne !?
Pozorny paradoks wynika z faktu, że pomiar narusza symetrię między układami: obserwujemy zegar, który jest związany z konkretnym układem odniesienia.
Obserwator O powie, że w układzie O':
- zegary nie są poprawnie zsynchronizowane
- wszystkie zegary chodzą wolniej niż powinny
Ale tak samo obserwator O' powie, że w układzie O:
- zegary nie są poprawnie zsynchronizowane
- wszystkie zegary chodzą wolniej niż powinny
Synchronizacja zegarów zależy od układu odniesienia.
Czy jesteśmy w stanie powiązać pomiary czasu i położenia w obu układach ?
Tak jak to robiliśmy w przypadku klasycznym (transformacja Galileusza)...
Transformacja Lorenza
Transformacja liniowa
Aby zachować niezmienniczość praw przyrody względem przesunięć w czasie i przestrzeni, transformacja współrzędnych między układami powinna mieć postać
- [math] \left(\begin{array}{c} t \\ x \\ y \\ z \end{array}\right) \; = \; L \cdot \left(\begin{array}{c} t' \\ x' \\ y' \\ z' \end{array}\right) [/math]
gdzie [math]L[/math] jest nieznaną macierzą współczynników transformacji ([math]4\times 4[/math])
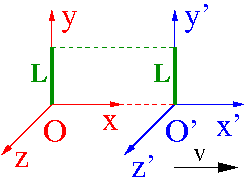
Wymiary poprzeczne
Zkładamy, że układ O' porusza się z prędkością [math]V[/math] w dodatnim kierunku osi X układu O.
Rozawżmy jednostkowe pręty umieszczone w obu układach wzdłuż osi Y (lub Z). Z symetrii zagadnienia, żaden obserwator nie może stwierdzić, że jego pręt jest dłuższy. Wnioskujemy z tego, że współrzędne zdarzeń prostopadłe do kierunku ruchu muszą się zachowywać:
- [math] y \; = \; y' [/math]
- [math] z \; = \; z' [/math]
Szukamy więc transformacji w ogólnej postaci:
- [math] t \; = \; A \; t' \;\; + \;\; B \; x' [/math]
- [math] x \; = \; C \; t' \;\; + \;\; D \; x'[/math]
- [math] y=y' \;\;\;\;\;\; z=z'[/math]
Dylatacja czasy
Przyjmijmy, że w obu układach pierwsze "tyknięcie" zegara świetlnego ma współrzędne [math](0,0,0,0)[/math].
Niech drugie "tyknięcie" w układzie O' ma współrzędne [math](t',0,0,0)[/math] (zegar spoczywa w początku układu).
W układzie O, rozważając bieg promienia świetlnego w zegarze dostaliśmy
- [math] t \; = \; \gamma \cdot t' [/math]
gdzie wprowadziliśmy tzw. współczynnik Lorentza
- [math] \gamma = \frac{1}{\sqrt{1-\beta^2}} [/math]
natomiast dla współrzędnej przestrzennej drugiego "tyknięcie"
- [math] x \; = \; \beta \cdot c t \; = \; \beta \gamma \cdot c t'[/math]
gdzie [math] \beta = \frac{v}{c} [/math]
Porównując otrzymane zależności z ogólną postacią transformacji otrzymujemy
- [math] A \; = \; \gamma[/math]
- [math] C \; = \; \beta \gamma c [/math]
Predkość światła
Przyjmijmy, że w chwili mijania się obserwatorów [math]t=t'=0[/math] z początku układów emitowane są dwa impulsy światła, zgodnie i przeciwnie do [math]\vec{v}[/math]. Dla obu obserwatorów rozchodzą się one z prędkością [math]c[/math].
Dla pierwszego impulsu mamy
- [math]x' = ct'[/math]
- [math]x = ct[/math]
Dla drugiego impulsu
- [math]x' = -ct'[/math]
- [math]x = -ct[/math]
Podstawiając założoną postać transformacji do równania opisującego rozchodzenie się impulsów w układzie O otrzymujemy (odpowiednio dla pierwszego i drugiego impulsu):
- [math]\displaystyle C t' + D (ct') = ~~c \cdot \left[ A t' + B (ct') \right][/math]
- [math]\displaystyle C t' - D (ct') = -c \cdot \left[ A t' - B (ct') \right][/math]
Dodając i odejmując stronami otrzymujemy:
- [math] B \; = \; \frac{1}{c^2} \; C \; = \; \frac{1}{c} \; \beta \gamma [/math]
- [math] D \; = \; A \; = \; \gamma [/math]
Transformacja Lorenza
Ostatecznie otrzymujemy transformację w postaci:
- [math] c\; t \; = \; \;\;\; \gamma \;c\; t' \;\; + \;\; \gamma \; \beta \; x' [/math]
- [math] x \; = \; \gamma \; \beta \; c\; t' \;\; + \;\;\;\;\; \gamma \; x' [/math]
- [math] y \; = \; y' [/math]
- [math] z\; = \; z'[/math]
Lub, w zapisie macierzowym:
- [math] \left(\begin{array}{c} c \; t \\ x \\ y \\ z \end{array}\right) \; = \; \left(\begin{array}{c} c \; \gamma \; t' \; + \; \gamma \; \beta \; x' \\ c \; \gamma \; \beta \; t' \; + \; \gamma \; x' \\ y' \\ z' \end{array}\right) \; = \; \left(\begin{array}{cccc} \gamma & \gamma \; \beta & 0 & 0 \\ \gamma \; \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} c\; t' \\ x' \\ y' \\ z'\end{array}\right) [/math]
[math]ct[/math] traktujemy jako "czwarty" wymiar (zazwyczaj zapisujemy jako wymiar "zerowy" - [math]x_0[/math]).
Transformację Lorenza można więc traktować jako pseudo-obrót w "płaszczyźnie" [math]ct[/math]-[math]x[/math] (dla ruchu wzdłuż osi X).