FizykaI FMiN/Zderzenia relatywistyczneZderzenia relatywistyczne
Zderzenia relatywistyczna
Dynamika relatywistyczna
Zasady zachowania
Relatywistyczne wyrażenie na pęd cząstki:
- [math] \vec{p} \; = \; m \;c \;\gamma \; \vec{\beta} \; = \; m \; \gamma \; \vec{V}[/math]
gdzie [math]\vec{\beta} = \frac{\vec{V}}{c}[/math]
Relatywistyczne wyrażenia na energię cząstki:
- energia kinetyczna: [math] E_{k} = m\; c^2 \; \left( \gamma - 1 \right) [/math]
- energia spoczynkowa: [math] E_{0} = m\; c^2 [/math]
- energia całkowita: [math] E = m\; c^2 \; \gamma [/math]
Dla dowolnego izolowanego układu obowiązują zawsze:
- zasada zachowania energii
- [math] \sum_{i } E_i \; = \; \sum_{i } \gamma_i \; m_i\; c^2 \; = \; const [/math]
- zasada zachowania pędu
- [math] \sum_{i} \vec{p}_i \; = \; \sum_{i } \gamma_i \cdot m_i\; \vec{V_i} \; = \; const [/math]
Transformacja
Zamiast rozważać niezależnie energię i pęd układu, wygodnie jest wprowadzić czterowektor energii-pędu:
- [math]{\cal E} \;=\; (E, c\vec{p}) \; = \;(E,cp_x,cp_y, cp_z) [/math]
Przy zmianie układu odniesienia, czterowektor energii-pędu podlega transformacji Lorentza identycznej z transformacją dla współrzędnych czasoprzestrzennych zdarzeń.
- [math] \left(\begin{array}{c} E \\ c\;p_x \\ c\;p_y \\ c\;p_z \end{array}\right) \; = \; \left(\begin{array}{c} \gamma \; E_\circ \; + \; \gamma \; \beta \; c \; p_{\circ,x} \\ \gamma \; \beta \; E_\circ \; + \; \gamma \; c \; p_{\circ,x} \\ c \; p_{\circ,y}\\ c \; p_{\circ,z} \end{array}\right) \; = \; \left(\begin{array}{cccc} \gamma & \gamma \; \beta & 0 & 0 \\ \gamma \; \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} E_\circ \\ c \; p_{\circ,x}\\ c \; p_{\circ,y}\\ c \; p_{\circ,z} \end{array}\right) [/math]
Widzimy, że energia całkowita odpowiada współrzędnej czasowej, zaś wektor pędu współrzędnym przestrzennym.
Przykład I
Rakieta lecąca w kierunku Ziemi z prędkoscią [math]v=0.6 c[/math] wystrzeliwuje w jej kierunku wiązkę protonów o energii [math]E = 100[/math] GeV. Masa protonu [math]m = 1GeV/c^2[/math]. Jaką energię protonów zmierzy obserwator na Ziemi?
Pęd protonu w układzie rakiety (z definicji masy niezmienniczej):
- [math] pc \; = \; \sqrt{E^2 - m^2c^4} = 99.9950 GeV[/math]
- [math] pc \approx E = 100 GeV[/math]
Współczynniki transformacji Lorentza z układu rakiety do układu Ziemi:
- [math] \beta = 0.6 \qquad \gamma = \frac{1}{\sqrt{1-\beta^2}} = 1.25 \qquad \beta\gamma = 0.75[/math]
Energia w układzie Ziemi:
- [math] E' = \gamma E + \beta \gamma pc \; \approx \; (\gamma + \beta \gamma ) E = 2 E = 200 GeV [/math]
Masa niezmiennicza
Jest to niezmiennik transformacji Lorenza, czyli wielkość, która nie zależy od wyboru układu odniesienia
- [math] M^2c^4 \; = \; s \; = \; E^2 \; - \; p^2 c^2[/math]
Dla dowolnego izolowanego układu fizycznego masa niezmiennicza jest zachowana (nie zmienia się w czasie). Wynika to z zasady zachowania energii i pędu.
Masa niezmiennicza jest podstawowym pojęciem w analizie zderzeń relatywistycznych, zwłaszcza w procesach nieelastycznych (produkcja nowych cząstek).
Masa niezmiennicza jest tożsama z energią układu w układzie środka masy ([math]P^\star = 0[/math]). Dla zderzających się cząstek mówimy o energii dostępnej w układzie środka masy.
Dla pojedynczej cząstki masa niezmiennicza jest tożsama z masą cząstki (energią spoczynkową).
Przykład
Jaka jest masa cząstki, która poruszając się z energią kinetyczną [math]E_k = 1.6[/math] GeV ma pęd [math]p = 2.4[/math] GeV/c ?
Z definicji masy niezmienniczej dla pojedynczej cząstki:
- [math] m^2c^4 \; = \; E^2 \; - \; p^2 c^2[/math]
Energię całkowitą wyrażamy przez energię kinetyczną:
- [math] m^2c^4 \; = \; (m c^2 + E_k)^2 \; - \; p^2 c^2 [/math]
- [math] m^2c^4 \; = \; m^2c^4 + 2 E_k m c^2 + E_k^2 \; - \; p^2 c^2[/math]
Otrzymujemy:
- [math] m c^2 \; = \; \frac{p^2 c^2 - E_k^2}{2 E_k} \; = \; \frac{(pc + E_k)(pc - E_k)}{2 E_k}[/math]
- [math] m c^2 \; = \; \frac{4GeV \cdot 0.8 GeV}{2 \cdot 1.6 GeV} \; = \; 1 GeV [/math]
Układ środka masy
Niech dane będą
- Energia układu cząstek: [math]E = \sum_i E_i[/math]
- Pęd układu cząstek: [math]\vec{P} = \sum_i \vec{p}_i[/math]
- Masa niezmiennicza tego układu: [math]M[/math]
Jak znaleźć układ środka masy (CMS), czyli układ w którym [math]\vec{P}^\star = 0[/math] ?
Wiemy, że w CMS energia i pęd dane są przez
- [math]E^\star = M, \;\;\; P^\star \equiv 0[/math]
Energia i pęd wiążą się z [math]E^\star[/math] i [math]P^\star[/math] przez transformacje Lorentza:
- [math] E \; = \; \gamma \; M [/math]
- [math] c\;P \; = \; \beta \; \gamma \; M [/math]
Otrzymujemy z przekształcenia tych zależności związki na wspólczynniki transformacji do układu środka masy:
- [math]\displaystyle \beta = \frac{c\; P}{E} [/math]
- [math]\displaystyle \gamma = \frac{E}{M\; c^2} [/math]
- [math]\displaystyle \beta \; \gamma = \frac{P}{M\; c} [/math]
Związki te obowiązują zarówno dla pojedyńczej cząstki jak i dowolnego układu cząstek!
Przykład
Z jaką prędkością porusza się elektron o energii [math]E=1GeV[/math] ([math]m_e\approx 0.5MeV[/math])?
Współczynnik Lorentza dla elektronu ([math]c\equiv 1 [/math]):
- [math] \gamma = \frac{1}{\sqrt{1-\beta^2}} \; = \; \frac{E}{m} = 2000 [/math]
Widzimy więc, że
- [math]1-\beta^2 = \frac{1}{\gamma^2} \; = \; \frac{m^2}{E^2} \qquad \ll 1 [/math]
Wnioskujemy, że prędkość elektronu jest bardzo bliska prędkości światła, [math]\beta \approx 1[/math], policzmy więc różnicę:
- [math] 1-\beta = \frac{1-\beta^2}{1+\beta} \; \approx \; \frac{1}{2\;\gamma^2} \; = \; \frac{m^2}{2\;E^2} = 1.25 \cdot 10^{-7} [/math]
Pęd elektronu:
- [math] p \; = \; \beta \gamma m \; = \; \beta E \; \approx\; E [/math]
Różnica między energią i pędem też dąży do zera:
- [math] E - p = (1-\beta) E \; \approx \; 10^{-7} E [/math]
Energia kinetyczna:
- [math] E_k \; = \; (\gamma -1 ) m \; = \; E - m \; \approx\; E [/math]
Różnica między energią całkowitą i kinetyczną:
- [math] E - E_k \; = \; m \; = \; \frac{1}{\gamma} E \; = \; 5 \cdot 10^{-4} E[/math]
Widzimy, że dla cząstki o energii [math]E \gg m c^2[/math] ([math] \gamma \gg 1[/math]) można przyjąć (przybliżenie ultrarelatywistyczne):
- [math]E \approx p c \approx E_k[/math]
Zderzenia elastyczne
Klasyfikacja zderzeń
W przypadku nierelatywistycznym zderzenia dzieliliśmy na:
- zderzenia elastyczne
- Zachowany jest pęd i energia kinetyczna.
- zderzenia nieelastyczne
- Zachowany jest pęd, natomiast energia kinetyczna zamieniana zostaje (częściowo) na inne formy energii (zazwyczaj ciepło).
W przypadku relatywistycznym
energia całkowita i
pęd
są zawsze zachowane.
Musimy zmodyfikować klasyfikację zderzeń.
Dzielimy je na:
- Zderzenia elastyczne
- Zderzenia typu [math]2 \rightarrow 2[/math] (dwie cząstki w stanie począstkowym i dwie w końcowym), przy czym cząstki po zderzeniu są takie same jak cząstki zderzające się (w szczególności nie zmieniają się ich masy: [math]m'_1 = m_1[/math] i [math]m'_2 = m_2[/math])
- przykład: [math]e^+ e^- \rightarrow e^+ e^- [/math]
- Zderzenia nieelastyczne
- Gdy cząstki w stanie końcowym są inne niż przed zderzeniem.
- przykład: [math]e^+ e^- \rightarrow \mu^+ \mu^- [/math]
Rozpraszanie elastyczne
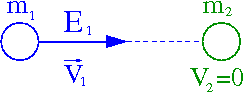
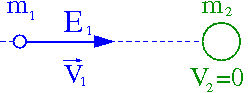
Rozważmy zderzenie "pocisku" o masie [math]m_1[/math] i energii [math]E_1[/math] z "tarczą" o masie [math]m_2[/math]. Dla układu dwóch ciał mamy ([math]c \equiv 1 [/math]):
- [math] E \;=\; E_1 + E_2 \; = \; E_1 + m_2 [/math]
- [math] P \; = \; P_1 \; = \; \sqrt{E_1^2 - m_1^2 } [/math]
- [math] M^2 \; = \; E^2 - P^2 \; = \; (E_1 + m_2)^2 - P_1^2 [/math]
- [math] \; = \; m_1^2 + m_2^2 + 2 \; E_1 \; m_2[/math]
Możemy policzyć współczynniki transformacji do układu środka masy:
- [math] \beta \; = \; \frac{P}{E} \; = \; \frac{\sqrt{E_1^2 - m_1^2 }}{E_1 + m_2}[/math]
- [math] \gamma \; = \; \frac{E}{M} \; = \; \frac{E_1 + m_2}{\sqrt{2 \; E_1 \; m_2 + m_1^2 + m_2^2 }} [/math]
- [math] \beta \gamma \; = \; \frac{P}{M} \; = \; \sqrt{\frac{E_1^2 - m_1^2 }{2 \; E_1 \; m_2 + m_1^2 + m_2^2 }} [/math]
Pęd obu ciał w układzie środka masy można zapisać jako:
- [math] p_1^\star \; = \; p_2^\star \; = \; \beta \gamma \; m_2 \; = \; \frac{P}{M} \; m_2 [/math]
- [math] (p^\star)^2 \; = \; \frac{(E_1^2 - m_1^2)\;m_2^2} {m_1^2 + m_2^2 + 2 \; E_1 \; m_2} [/math]
Energie obu ciał w układzie środka masy:
- [math] E_2^\star \; = \; \gamma \; m_2 \; = \; \frac{E}{M} \; m_2 [/math]
- [math] \; = \; \frac{(E_1 + m_2) m_2}{\sqrt{2 \; E_1 \; m_2 + m_1^2 + m_2^2 }} [/math]
- [math]E_1^\star \; = \; M - E_2^\star [/math]
- [math] \; = \; \frac{E_1 m_2 + m_1^2}{\sqrt{2 \; E_1 \; m_2 + m_1^2 + m_2^2 }} [/math]
Jeśli spełniona ma być zasada zachowania pędu i zasada zachowania energii to, tak jak w przypadku klasycznym
- [math] p_1^\star \; = \; p_2^\star \; = \; {p'}^\star_1 \; = \; {p'}^\star_2 [/math]
W układzie środka masy wartości pędów nie ulegają zmianie!
Zakładamy tutaj, że masy cząstek nie zmieniają siem, [math]m'_1 = m_1[/math] i [math]m'_2 = m_2[/math] (rozpraszanie elastyczne).
Przypadek [math]m_1 = m_2[/math]
Uzyskane wyrażenia bardzo się upraszczają dla zderzeń cząstek o równej masie. Energia, pęd i masa niezmiennicza układu dwóch cząstek:
- [math] E \; = \; E_1 + m [/math]
- [math] P \; = \; P_1 \; = \; \sqrt{E_1^2 - m^2 } [/math]
- [math] M^2 \; = \; E^2 - P^2 \; = \; 2 \; E_1 \; m \; + \; 2 \; m^2 [/math]
Współczynniki transformacji do CMS:
- [math]\gamma \; = \; \sqrt{\frac{E_1+m}{2m}} [/math]
- [math]\beta \; = \; \sqrt{\frac{E_1-m}{E_1+m}} [/math]
- [math]\beta \;\gamma \; = \; \sqrt{\frac{E_1-m}{2m}}[/math]
Energia i pęd obu ciał w układzie środka masy
(z transformacji Lorenza dla spoczywającego ciała):
- [math] p^\star \; = \; \gamma \; \beta \; m [/math]
- [math] E^\star \; = \; \gamma \; m [/math]
- [math] (p^\star)^2 \; = \; \frac{1}{2}\; m \; (E_1 - m) [/math]
- [math] (E^\star)^2 \; = \; \frac{1}{2}\; m \; (E_1 + m) [/math]
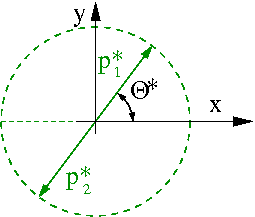
Wprowadźmy w układzie środka masy kąt [math]\theta^\star[/math] opisujący kierunek rozproszenia pierwszej cząstki.
Możemy teraz wypisać składowe czterowektora energii-pędu dla pierwszej cząstki w CMS:
- [math] E_1^\star \; = \; \gamma \; m [/math]
- [math] p_{1,x}^\star \; = \; \gamma \; \beta \; m \; \cos \theta^\star [/math]
- [math] p_{1,y}^\star \; = \; \gamma \; \beta \; m \; \sin \theta^\star [/math]
- [math] p_{1,z}^\star \; = \; 0 [/math]
Transformacja Lorentza do układu laboratoryjnego daje nam:
- [math] p_{1,x} \; = \; \gamma \; p_{1,x}^\star + \gamma \; \beta \; E_1^\star [/math]
- [math] \; = \; \gamma^2 \; \beta \; m \; ( 1 + \cos \theta^\star ) [/math]
- [math] p_{1,y} \; = \; \gamma \; \beta \; m \; \sin \theta^\star [/math]
Zauważmy też, że
- [math] \gamma^2 \; \beta \; m = \frac{1}{2} P [/math]
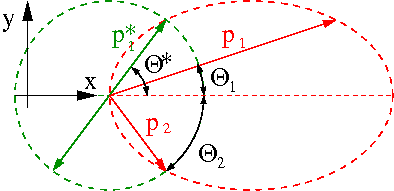
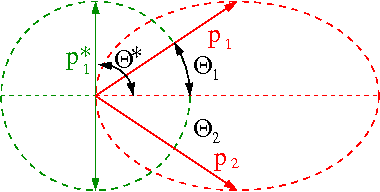
Możliwe wartości [math]p_{1,x}[/math] i [math]p_{1,y}[/math] spełniają warunek: [math]\gamma^2 \; p_{1,y}^2 + \left(p_{1,x} - \frac{P}{2}\right)^2 \; = \; \left(\frac{P}{2}\right)^2[/math]
Warunek ten odpowiada równaniu elipsy w przestrzeni pędów. Transformacja Lorenza "spłaszcza" rozkład pędów wzdłuż kierunku ruchu pocisku (w przypadku klasycznym mieliśmy okrąg).
Kąty rozproszenia mierzone w LAB (liczone ze stosunku poprzecznej i podłużnej składowej):
- [math] \tan \theta_1 \; = \; \frac{\sin \theta^\star} {\gamma ( 1 + \cos \theta^\star)} [/math]
- [math]\tan \theta_2 \; = \; \frac{\sin \theta^\star} {\gamma ( 1 - \cos \theta^\star)} [/math]
Możemy wyznaczyć kąt pomiędzy cząstkami po zderzeniu:
- [math] \tan ( \theta_1 + \theta_2 ) \; = \; \frac{ 2 \gamma } { \sin \theta^\star \; ( \gamma^2 - 1) } [/math]
W przypadku rozproszenia pod kątem prostym w CMS ([math]\theta^\star = \frac{\pi}{2}[/math])
- [math] \tan \theta \; = \; \frac{1}{\gamma} \; \lt \; 1 [/math]
- [math] \theta_1 \; + \; \theta_2 \; \lt \; \frac{\pi}{2} [/math]
W przypadku klasycznym kąt między rozproszonym pociskiem i tarczą, dla równych mas, zawsze był równy [math]\frac{\pi}{2}[/math]. W przypadku relatywistycznym kąty rozproszenia są mniejsze.
Dla dużych energii pocisku, [math]\gamma \rightarrow \infty[/math], kąt między cząstkami
- [math] \tan ( \theta_1 + \theta_2 ) \; \rightarrow \; \frac{ 2 }{ \gamma \; \sin \theta^\star} \rightarrow 0 [/math]
W granicy ultrarelatywistycznej rozproszenie zachodzi pod bardzo małymi kątami!
Przykład
Elektron o energii [math]E=10[/math] GeV rozprasza się elastycznie na spoczywającym elektronie ([math]m_e = 0.5[/math] MeV). Jaki kąt rozproszenia zostanie zmierzony w układzie laboratoryjnym jeśli w CMS rozproszenie nastapiło pod kątem prostym?
Masa niezmiennicza układu:
- [math]M \; = \; \sqrt{2 \; E \; m \; + \; 2 \; m^2} \approx \sqrt{2 \; E \; m } \; = \; 100 MeV [/math]
Współczynnik transformacji:
- [math] \gamma = \frac{E + m}{M} \; \approx \; \frac{E}{M} = 100[/math]
co odpowiada
- [math] 1-\beta \approx 5\cdot 10^{-5}[/math]
Energia i pęd w CMS:
- [math] E^\star \; = \; \gamma m \; = \; 50 MeV \; \; p^\star \approx E^\star [/math]
Transformacja do układu laboratoryjnego dla cząstki rozproszonej pod kątem orisrtn w CMS (kładąc [math]p^\star_x = 0[/math], [math]p^\star_y = p^\star[/math]):
- [math] p_x = \beta \gamma E^\star + \gamma p^\star_x \approx \gamma E^\star[/math]
- [math] p_y = p^\star_y \approx E^\star [/math]</math>
Kąt rozproszenia wynosi więc:
- [math] \tan \theta \; = \; \frac{p_y}{p_x} \; = \; \frac{1}{\gamma} \; = \; 0.01 [/math]
- [math] \theta \approx 0.6^\circ[/math]
Przypadek [math]m_1 \ll E_1 \sim m_2[/math]
Rozważmy zderzenie elastyczne z ciężką "tarczą" lekkiego "pocisku" ([math]m_1 \ll m_2[/math]) o wysokiej energii ([math]E_1 \sim m_2[/math])
Jest to sytuacja z jaką często mamy do czynienia w zderzeniach fizyki cząstek (rozpraszanie elektonów, mionów lub neutrin na tarczach jądrowych).
Pomijając wyrazy z [math]m_1[/math] mamy:
- [math] E \; = \; E_1 + m_2 [/math]
- [math] P \; = \; \sqrt{E_1^2 - m_1^2 } \approx E_1 [/math]
- [math] M^2 \; = \; m_1^2 + m_2^2 + 2 \; E_1 \; m_2 [/math]
- [math] \; \approx \; 2 \; E_1 \; m_2 + m_2^2 [/math]
Współczynniki transformacji do układu środka masy
(dla [math]m_1 \rightarrow 0 [/math]):
- [math] \gamma \; = \; \frac{E_1+m_2}{\sqrt{2E_1 m_2 + m_2^2}} [/math]
- [math] \beta \; = \; \frac{E_1}{E_1+m_2} [/math]
- [math] \beta \;\gamma \; = \; \frac{E_1}{\sqrt{2E_1 m_2 + m_2^2}} [/math]
Pęd pocisku i tarczy w układzie środka masy:
- [math] p^\star \; = \; \beta \;\gamma \; m_2 \; = \; \frac{E_1 m_2}{\sqrt{2E_1 m_2 + m_2^2}} [/math]
Transformacja rozproszonego pocisku do układu laboratoryjnego daje nam:
- [math] p_{1,x} \; = \; \gamma \; p_{1,x}^\star + \gamma \; \beta \; E_1^\star \; = \; \gamma \; p^\star ( \beta + \cos \theta^\star ) [/math]
- [math] p_{1,y} \; = \; p^\star \; \sin \theta^\star [/math]
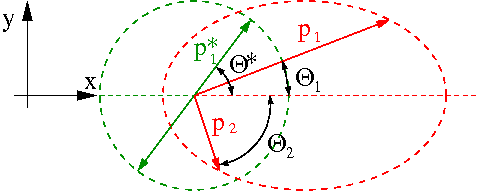
Możliwe wartości [math]p_{1,x}[/math] i [math]p_{1,y}[/math] spełniają więc warunek:
- [math]\left(\gamma \; p_{1,y} \right)^2 + \left(p_{1,x} - \gamma \; \beta \; p^\star \right)^2 \; = \; \left( \gamma p^\star \right)^2[/math]
Odpowiada to ponownie równaniu elipsy.
W granicy [math]\beta \rightarrow 1[/math] ([math]E_1 \gg m_2[/math]) pocisk rozprasza się zawsze ``do przodu" ([math]p_{1,x} \ge 0[/math])!
Nawet dla [math]m_1 \ll m_2[/math], jeśli [math]E_1 \sim m_2[/math] pocisk może przekazać tarczy znaczną część swojej energii. Rysunek obok pokazuje możliwe wartości pędu dla przypadku [math]E_1 = 3 \; m_2[/math], [math]m_1 = 0[/math]. Dla [math]E_1 \gg m_2[/math] nawet bardzo lekka sonda może "wybić" cząstkę tarczy...
Masa cząstki pocisku, dla dużych energii, przestaje być istotna.
Rozpraszanie nierelatywistyczne
Przypomnijmy, że w podejściu klasycznym, w granicy [math]m_1 \ll m_2[/math] tarcza przejmuje bardzo niewielką część energii pocisku. Rozproszony pocisk ma praktycznie niezmienioną energię i wartość pędu.
Przykład
Elektron o energii [math]E_e = 50[/math] GeV rozprasza się na spoczywającym protonie ([math]m_p = 1[/math] GeV).
Jaka jest maksymalna energia jaką może uzyskać proton?
Masa niezmiennicza układu
- [math]M \; = \; \sqrt{2 \; E_e \; m_p \; + \; m_p^2} \; \approx \; \sqrt{2 \; E_e \; m_p } \; = \; 10 GeV [/math]
Współczynnik transformacji:
- [math]\gamma = \frac{E_e + m_p}{M} \; = \; 5.1 [/math]
- [math] \beta \gamma = \frac{p_e}{M} = 5 [/math]
Energia i pęd protonu w CMS:
- [math] E_p^\star \; = \; \gamma m_p \; = \; 5.1\; GeV [/math]\; \;
- [math] p^\star = \beta \gamma m = \; 5\; GeV [/math]
Transformacja do LAB (maksymalna energia gdy [math]p^\star_x = p^\star[/math]):
- [math] E' \; = \; \gamma E^\star + \beta \gamma p^\star_x \; = \; \gamma^2 m_p + \beta^2 \gamma^2 m_p \approx 51 \; GeV [/math]
Proton może przejąć praktycznie całą energię elektronu!
Nie pomijając członu [math]m_p^2[/math] w wyrażeniu na masę niezmienniczą otrzymujemy dokładniejszy wynik
- [math] E' \approx 50.50 \; GeV [/math]
rozproszony elektron zachowa 1% swojej energii całkowitej...
Zderzenia nieelastyczne
Klasyfikacja zderzeń
Zderzenia elastyczne to reakcje typu [math]2 \rightarrow 2[/math], w których cząstki rozproszone są takie same jak cząstki zderzające się. W szczególności: [math]m'_1 = m_1[/math] i [math]m'_2 = m_2[/math]
W zderzeniach cząstek jest to jednak wyjątek (!)
W oddziaływaniach cząstek elementarnych, zwłaszcza przy wysokiej energii, obserwujemy bardzo wiele reakcji, w których powstają nowe cząstki:
- Rozpady cząstek: [math]a \rightarrow b + c[/math]
- Produkcja pojedyńczej cząstki (tzw. "rezonansu"): [math]a + b \rightarrow c[/math]
- Rozproszenie nieelastyczne dwóch cząstek: [math]a + b \rightarrow c + d [/math] (przy czym jedna z cząstek na końcu może być cząstką stanu początkowego)
- Produkcja wielu cząstek: [math]a + b \rightarrow X [/math] (gdzie [math]X[/math] oznacza dowolny stan wielocząstkowy)
Świat cząstek elementarnych
Zanim zajmiemy się szerzej zderzeniami nieelastycznymi cząstek poznajmy obiekty, które w takich zderzeniach mogą uczestniczyć.
Fermiony
Fermiony są podstawowymi składnikami otaczającej nas materii. Świat "codzienny" zbudowany jest z 3 fundamentalnych "cegiełek": elektron oraz kwarków [math]u[/math] i [math]d[/math].
Elektron występuje jako cząstka swobodna, natomiast kwarki są "uwięzione" w nukleonach. Każdy nukleony składa się z 3 kwarków: proton to (uud), neutron - (udd).
Fizyka cząstek znalazła łącznie 12 fundamentalnych "cegiełek" materii, cząstek zwanych fermionami (cząstek o spinie 1/2). Znamy 6 leptonów i 6 kwarków, które można podzielić na 3 tzw. pokolenia:
| leptony | kwarki | |||
|---|---|---|---|---|
| pokolenie 1 | [math]e[/math] | [math]\nu_{e}[/math] | d | u |
| elektron | neutrino el. | down | up | |
| pokolenie 2 | [math]\mu[/math] | [math]\nu_{\mu}[/math] | s | c |
| mion | neutrino mionowe | strange | charm | |
| pokolenie 3 | [math]\tau[/math] | [math]\nu_{\tau}[/math] | b | t |
| taon | neutrino taonowe | beauty | top | |
| ładunek [e] | [math]-1[/math] | 0 | [math]-1/3[/math] | [math]+2/3[/math] |
Każda z wymienionych cząstek ma też swoją antycząstkę (kolejne 12).
Wszystkie leptony obserwujemy jako cząstki swobodne. Natomiast kwarki są zawsze "uwięzione" w hadronach (cząstkach oddziałujących silnie)
Bozony
"Cegiełki" materii oddziałują ze sobą
poprzez wymianę nośników oddziaływań.
Nośnik przekazuje część energii i/lub pędu jednej cząstki
drugiej cząstce.
| oddziaływanie | źródło | nośnik | moc | |
|---|---|---|---|---|
| grawitacyjne | masa | grawiton | G | [math]10^{-39}[/math] |
| elektromagnetyczne | ładunek el. | foton | [math]\gamma[/math] | [math]10^{-2}[/math] |
| silne | "kolor" | gluony | [math]g[/math] | 1 |
| słabe | "ładunek słaby" | "bozony pośredniczące" | [math]W^{\pm}[/math], [math]Z^{\circ}[/math] | [math]10^{-7}[/math] |
gdzie jako "moc" pokazano przykładowe porównanie wielkości oddziaływań dla dwóch sąsiadujących protonów
Rozpady cząstek
Rozawżmy rozpad cząstki o masie [math]M[/math] na [math]n[/math] cząstek o masach [math]m_i[/math] {([math]i = 1 \ldots n[/math])}.
Masa niezmiennicza przed rozpadem:
- [math]{\cal M}_i =M[/math]
Masa niezmiennicza po rozpadzie:
- [math] {\cal M}_f^2 \; = \; \left(\sum_i E_i \right)^2 \; - \; \left(\sum_i \vec{p}_i \right)^2 [/math]
- [math] \; = \; \sum_i E_i^2 \; + \; 2 \;\sum_i \sum_{j\gt i} E_i \;E_j \; - \; \sum_i p_i^2 \; - \; 2 \;\sum_i \sum_{j\gt i} \vec{p}_i \; \vec{p}_j [/math]
Dla dowolnej pary cząstek [math]i[/math], [math]j[/math] mamy ([math]E_i^2 = p_i^2 + m_i^2[/math]):
- [math] E_i \; E_j = \sqrt{(p_i^2 +m_i^2)(p_j^2 +m_j^2)} [/math]
- [math] \; = \; \sqrt{(p_i p_j +m_i m_j)^2 + (p_i m_j - p_j m_i)^2 } [/math]
- [math] \;\; \ge \; p_i\; p_j\; +\; m_i \;m_j [/math]
Czyli
- [math] E_i \; E_j \;-\; \vec{p}_i \vec{p}_j \; \ge \; E_i \; E_j \;-\; p_i p_j \; \ge \; m_i \;m_j [/math]
Ostatecznie otrzymujemy więc warunek:
- [math] \displaystyle {\cal M}_f^2 \ge \sum_i m_i^2 + 2 \;\sum_i \sum_{j\gt i} m_i \;m_j = \left( \sum_i m_i \right)^2 = s_{min} [/math]
Warunek konieczny, aby mógł mieć miejsce rozpad do określonego stanu cząstkowego
można więc zapisać w postaci:
- [math] M \; \ge \; \sum_i m_i \qquad = \sqrt{s_{min}}[/math]
gdzie [math]s_{min}[/math] jest minimalną wartością kwadratu masy niezmienniczej stanu końcowego.
Rozważmy najprostszy przypadek rozpadu dwuciałowego. W układzie rozpadającej się cząstki produkty rozpadu mają równe co do wartości lecz przeciwnie skierowane pędy:
- [math]\vec{p}_1 = -\vec{p}_2[/math]
Jaka będzie wartość pędu produktów rozpadu [math]p = |\vec{p}_1| = |\vec{p}_2|[/math] ?
Wyraźmy masę niezmienniczą przez pęd produktów:
- [math]M^2 \; = \; (E_1 + E_2)^2 - (p_1 - p_2)^2 \; = \; m_1^2 + m_2^2 + 2\sqrt{(p^2 +m_1^2)(p^2 +m_2^2)} + 2 p^2 [/math]
Wydzielając pierwiastek i podnosząc do kwadratu
- [math] (M^2 -m_1^2 - m_2^2 -2p^2 )^2 \; = \; 4(p^2 +m_1^2)(p^2 +m_2^2) [/math]
Większość wyrazów z pędem skróci się. Zostaje
- [math]4 M^2 p^2 \; = \; (M^2 -m_1^2 - m_2^2)^2 - 4 m_1^2 m_2^2 [/math]
Ostatecznie otrzymujemy:
- [math] p \; = \; \frac{\sqrt{(M^2 - (m_1+m_2)^2)(M^2 - (m_1 - m_2)^2)}}{2\;M} [/math]
Wyrażenie to bardzo się upraszcza w przypadku rozpadu na dwie cząstki
o równych masach, [math]m_1 = m_2 = m[/math]:
- [math] p \; = \; \frac{\sqrt{(M^2 - 4m^2)M^2}}{2\;M} \; = \;\sqrt{ \left(\frac{M}{2}\right)^2 - m^2}[/math]
Energia produktów rozpadu wyniesie wtedy
- [math] E = \frac{M}{2} [/math]
Z kolei w granicy, gdy jeden z produktów rozpadu jest bardzo lekki,
[math]m_1 \ll m_2 \sim M[/math],
otrzymujemy:
- [math] p \; \approx \; \frac{\sqrt{(M^2 - m_2^2)^2}}{2\;M} \; = \; \frac{M}{2} \; - \; \frac{m_2^2}{2M} \qquad\qquad \approx E_1 [/math]
Energie cząstek po rozpadzie nie są równe !
Mierząc pęd (lub energię) jednego z produktów rozpadu, możemy wnioskować o masach pozostałych cząstek.
Przykład
Pion [math]\pi^+[/math] o masie [math]m_\pi = 140[/math] MeV rozpada się na mion [math]\mu^+[/math] (o macie [math]m_\mu = 106[/math] MeV) i bezmasowe neutrino:
- [math] \pi^+ \; \rightarrow \mu^+ \; + \; \nu_\mu [/math]
Pędy produktów rozpadu:
- [math] p \; = \; \frac{m_\pi^2 - m_\mu^2}{2\;m_\pi} \; \approx \; 30 \; MeV[/math]
Energie liczymy z definicji masy niezmienniczej ([math] m^2 \; = \; E^2 - p^2 [/math]):
- [math] E_\mu \; = \; \sqrt{p^2 + m_\mu^2}\; \approx\; 110 \; MeV [/math]
- [math] E^k_\mu \;= \;4 \; MeV [/math]
- [math] E_\nu \; = \; E^k_\nu \; = \; \sqrt{p^2 + m_\nu^2}\; = \;p\; = \;30 \; MeV [/math]
Neutrino wynosi większość energii kinetycznej!
Prawo rozpadu
Wszystkie cząstki danego rodzaju (np. elektrony lub neutrony) są identyczne. Nie mają też "pamięci" - ich własności nie zależą od czasu. Dla cząstek nietrwałych oznacza to, że prawdopodobieństwo ich rozpadu w zadanym przedziale czasu jest zawsze takie samo.
Rozważmy bardzo mały przedział czasu [math]dt[/math]
(znacznie mniejszy niż typowy czas rozpadu).
Jeśli próbka zawiera [math]N[/math] cząstek to
liczba oczekiwanych rozpadów musi być proporcjonalna do
[math]N[/math] i do
[math]dt[/math]:
- [math] dN \; = \; N(t+dt) - N(t) \; = \; - \alpha \; N \; dt [/math]
Całkując to równanie otrzymujemy:
- [math] \frac{dN}{N} \; = \; - \alpha \; dt [/math]
- [math] \ln N \; = \; - \alpha \; t \; + \; C [/math]
Ostatecznie otrzymujemy prawo rozpadu promieniotwórczego
- [math] N(t) \; = \; N(0) \cdot e^{-\alpha t} [/math]
Pozostaje nam jednak nieznany parametr [math]\alpha[/math], który musimy
powiązać z własnościami cząstki. Prawdopodobieństwo rozpadu na jednostkę czasu
(dla pojedynczej cząstki) dane jest przez:
- [math] p(t) \; = \; \alpha \; e^{-\alpha t} [/math]
Parametr [math]\alpha[/math] możemy więc powiązać ze średnim czasem życia cząstki cząstki:
- [math] \tau \; = \; \langle t \rangle \; = \; \int_0^{\infty} t \cdot p(t)dt = \frac{1}{\alpha} [/math]
Ptrzymujemy więc wzory na prawdopodobieństwo rozpadu
- [math] p(t) = \frac{1}{\tau} \; e^{-t/\tau} [/math]
oraz
- [math] N(t) = N_0 \cdot e^{- t/\tau} [/math]
Jeśli cząstka o masie [math]m[/math] i średnim czasie życia [math]\tau[/math] (zawsze defniowanym w układzie cząstki) ma w układzie obserwatora O' energię [math]E[/math] i pęd [math]p[/math], to obserwator zmierzy:
- [math] N(t') \; = \; N_0 \cdot e^{- \frac{t'}{\gamma \tau}} \;= \; N_0 \cdot e^{- \frac{m t'}{E \tau}}[/math]
- [math] \langle t' \rangle \; = \; \gamma \; \tau \; = \; \frac{E}{m} \; \tau [/math]
zgodnie z formułą na dylatację czasu. Możemy też zdefiniować średnią drogę swobodną: [math]\lambda \; = \; \langle v t'\rangle \; = \; \beta \; \gamma \; c \tau \; = \; \frac{p}{m} \; c\tau [/math]
Przykład
Jaki powinien być pęd mionu produkowanego w górnych warstwach atmosfery ([math]h=20[/math] km), żeby mógł dolecieć do powierzchni Ziemi zanim się rozpadnie?
Prawdopodobieństwo rozpadu w funkcji odległości:
- [math] p(x) \; = \; \frac{1}{\lambda} \; e^{-x/\lambda} [/math]
Prawdopodobieństwo, że mion doleci do powierzchni Ziemi:
- [math] P(x\gt h) \; = \; \int_h^{\infty} p(x)dx \; = \; e^{-h/\lambda}[/math]
Prawdopodobieństwo to jest formalnie niezerowe dla dowolnego pędu. Duże szanse dolecieć mają jednak tylko miony, dla których [math]\lambda \gt h[/math]:
- [math] \frac{p}{m} \; c\tau \gt h [/math]
- [math] \; p \gt \frac{h}{c\tau} m [/math]
Dla mionu: [math]\tau = 2.2 \; \mu s[/math] ([math]c \tau \approx 660 \; m[/math]), [math]m \approx 100[/math] MeV:
- [math] p \; \gt \; \frac{h}{c\tau} m \;\approx \; 30\cdot m \;= \; 3 \;GeV[/math]
Zderzenia [math]e^+ e^-[/math]
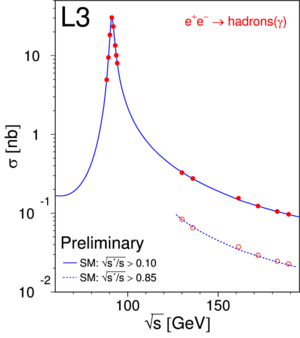
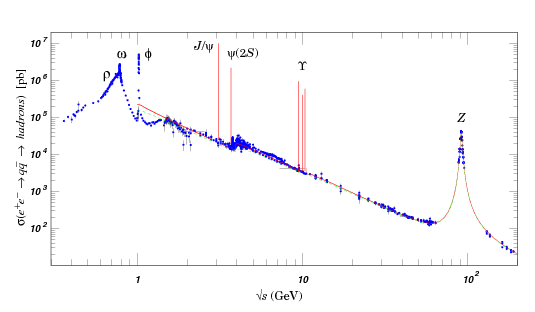
Przekrój czynny na produkcję kwarków (rejestrowanych w postaci hadronów) w funkcji dostępnej energii w zderzeniu [math]e^+ e^-[/math]:
W całym zakresie zbadanych energii mamy niezerowy przekrój czynny na produkcję kwarków. Proces ten opisujemy jako anihilację [math]e^+ e^-[/math] w wirtualny foton, który następnie rozpada sie na parę [math]q \bar{q}[/math]. Schematycznie przedstawia to poniższy diagram:
Produkcja rezonansów
Przy pewnych wartościach [math]\sqrt{s}[/math] obserwujemy wzrost produkcji kwarków o kilka rzędów wielkości.
Jest to efekt rezonansowej produkcji cząstek, którą można przedstawić schematycznie na diagramie:
Przy czym cząstka [math]J/\Psi[/math] jest nietrwała i rozpada się nastepnie (np. na parę kwarków). Aby w zderzeniu dwóch cząstek powstała jedna cząstka (np: [math] e^+ e^- \rightarrow J/\Psi[/math]) masa niezmiennicza zderzających się cząstek musi być równa masie cząstki którą produkujemy
- [math] \sqrt{s} = m_{J/\Psi} [/math]
Najbardziej masywnym rezonansem produkowanym dotychczas w zderzeniach [math]e^+ e^-[/math] jest bozon [math]Z^\circ[/math]:
- [math] e^+ e^- \; \rightarrow \; Z^\circ \; \rightarrow q \bar{q} [/math]
Maksimum przekroju czynnego obserwujemy dla
- [math] \sqrt{s} \; = \; m_Z [/math]
ale ma ono skończoną szerokość, opisaną tzw. rozkładem Breita-Wignera:
- [math] \sigma(s) \; \sim \; \frac{M_Z^2 \Gamma^2} {(s - M_Z^2)^2 + M_Z^2 \Gamma^2}[/math]
Szerokość rezonansu wiąże się (zasada nieoznaczoności) z czasem życia produkowanej cząstki: [math] \Gamma \cdot \tau = h [/math]
Produkcja wielu cząstek
Aby w zderzeniu dwóch cząstek powstały dwie lub więcej nowych cząstek, np:
- [math] e^+ \; e^- \; \rightarrow \; W^+ \; W^- [/math]
masa niezmiennicza zderzających się cząstek musi być większa lub równa sumie mas produkowanych cząstek:
- [math] \sqrt{s} \; \ge \; \sum_i m_i [/math]
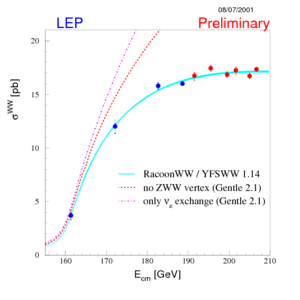
W przypadku produkcji par bozonów
- [math] e^+ e^- \rightarrow W^+ W^-[/math]
masa niezmiennicza zderzających się elektronów musi spełniać warunek
- [math]\sqrt{s} \ge 2 \; m_W \approx[/math] 160 GeV
Energia dostępna
Mase niezmienniczą zderzających się cząstek [math]\sqrt{s}[/math] określamy też jako energię dostępną w układzie środka masy. Energia dostępna jest to część energii kinetycznej, która może zostać zamieniona na masę (energię spoczynkową) nowych cząstek. [math]\sqrt{s}[/math] mówi nam ile energii możemy zużyć na wyprodukowanie nowych cząstek.
Przykład
Aby wyprodukować antyproton w reakcji
- [math] p \; p \; \rightarrow p \; p \; p \; \bar{p} [/math]
musimy mieć
- [math] \sqrt{s} \; \ge \; 4 \; m_p [/math]
Należy zwrócić uwagę, że liczymy wszystkie cząstki w stanie końcowym, także cząstki pierwotne.
Określoną wartość energii dostępnej możemy uzyskać na rózne sposoby:
Zderzenia z tarczą
Cząstka "pocisk" o energii [math]E[/math] uderza w nieruchomą tarczę. Kwadrat masy niezmienniczej:
- [math] s \; = \; 2 \; E_1 \; m_2 + m_1^2 + m_2^2 [/math]
w granicy [math] E_1 \gg m_1 \sim m_2 [/math]
- [math] s \; \approx \; 2 \; E_1 \; m_2 [/math]
Wiązki przeciwbieżne
Zderzenia wiązek o energiach [math]E_1[/math] i [math]E_2[/math]:
- [math] s \; = \; 2 \; E_1 \; E_2 + 2 \; p_1 \; p_2 + m_1^2 + m_2^2 [/math]
w granicy [math] E_1 \sim E_2 \gg m_1 \sim m_2 [/math]
- [math] s \; \approx \; 4 \; E_1 \; E_2 [/math]
Uzyskujemy dużo wyższe wartości energii dostępnej niż w przypadku zderzenia "z tarczą"!!!
Przykład
Wiązka protonów o energii 50 GeV ([math]\approx 50 \; m_p[/math])
- na tarczy wodorowej (protony):
- [math]\sqrt{s} \approx \sqrt{2 E m_p} \approx 10 GeV \approx 10 \; m_p[/math]
- dwie wiązki przeciwbieżne:
- [math]\sqrt{s} \approx \sqrt{4 E \cdot E} = 2 \; E = 100 GeV \approx 100 \; m_p[/math]
Energia progowa
Jest to minimalna energia wiązki [math]E_{min}[/math] przy której możliwa jest dana reakcja. Sprowadza się to do warunku przekroczenia przez masę niezmienniczą pocisku i tarczy minimalnej masy niezmienniczej danej przez masy produktów reakcji. Kwadrat minimalnej masy niezmienniczej:
- [math] s_{min} \; = \; \left( \sum_i m_i \right)^2 [/math]
Zderzenia z tarczą
W zderzeniach z nieruchomą tarczą:
- [math] s_{min} \; = \; 2 \; E_{min} \; m_2 + m_1^2 + m_2^2 [/math]
Możemy policzyć jaka jest minimalna energia całkowita pocisku:
- [math] E_{min} \; = \; \frac{s_{min} - ( m_1^2 + m_2^2) }{2 \; m_2 } \; = \; \frac{ \left( \sum_i m_i \right)^2 - ( m_1^2 + m_2^2) }{2 \; m_2 } [/math]
Minimalna energia kinetyczna pocisku:
- [math] E_{k, min} \; = \; E_{min} - E_\circ \; = \; \frac{ \left( \sum_i m_i \right)^2 - ( m_1 + m_2)^2 }{2 \; m_2 } [/math]
Minimalna energia kinetyczna pocisku, w zderzeniach z tarczą, więże się
z przyrostem masy:
- [math] 2 \; m_2 \; E_{k, min} \; = \; \left( \sum_i m_i \right)^2_{koncowe} - \;\; \left( \sum_i m_i \right)^2_{poczatkowe} [/math]
Energia kinetyczna pocisku jest "zużywana" na zwiększenie masy układu...
Przykład 1
Produkcja anty-protonów w reakcji
- [math] p \; p \; \rightarrow p \; p \; p \; \bar{p} [/math]
Minimalna masa niezmiennicza: [math] \sum_i m_i = 4 \; m_p [/math]
Podstawiając otrzymujemy:
- [math] E_{min} \; = \; \frac{ (4 \; m_p)^2 - ( m_p^2 + m_p^2) }{2 \; m_p } \; = \; 7 \; m_p [/math]
- [math] E_{k, min} \; = \; E_{min} - m_p \; = \; 6\; m_p \qquad \approx 5.63\;GeV [/math]
Wiązki przeciwbieżne
Dla wiązek przeciwbieżnych (dla uproszczenia przyjmujemy [math]E_1 = E_2[/math], [math]m_1 = m_2[/math]) mamy
- [math] s_{min} \; \approx \; 4 \; E_1 \; E_2 \; = \; 4 \; E_{min}^2 [/math]
Minimalna energia wiązki przy której możliwe jest wyprodukowanie danego stanu dana jest przez
- [math] E_{min} \; = \; \frac{1}{2}\sqrt{s_{min}} \; = \; \frac{1}{2}\sqrt{(\sum_i m_i)^2} \; = \; \frac{1}{2} \sum_i m_i [/math]
Minimalna energia kinetyczna
- [math] E_{k,min} \; = \; \frac{1}{2} \left[ \left( \sum_i m_i \right)_{koncowe} - \;\; \left( \sum_i m_i \right)_{poczatkowe} \right] [/math]
Należy zauważyć, że energia rośnie liniowo z masą produkowanego stanu (na tarczy: kwadratowo!). Dużo niższe energie potrzebne są do wytworzenia tego samego stanu w zderzeniach wiązek przeciwbieżnych
Przykład 1 (c.d.)
Produkcja anty-protonów w reakcji
- [math] p \; p \; \rightarrow p \; p \; p \; \bar{p} [/math]
Minimalna energia kinetyczna protonów w przypadku zderzenia wiązeg przeciwbieżnych
- [math] E_{k, min} \; = \; \frac{1}{2} \left[ 4 m_p - 2 m_p \right] \; = m_p \qquad \approx 0.94\;GeV [/math]
(na tarczy: 5.63 GeV)
Przykład 2
Produkcja par bozonów [math]W^+ W^-[/math] w zderzeniach elektron-pozyton:
- [math] e^+ \; e^- \rightarrow W^+ \; W^- [/math]
Gdybyśmy chcieli użyć pojedyńczej wiązki pozytonów i tarczy, minimalna energia wiązki wyniosłaby ([math]m_W = 80.4\; GeV[/math], [math]m_e = 0.000511\; GeV [/math])
- [math] E_{min} \; = \; \frac{ (2 \; m_W)^2 - ( m_e^2 + m_e^2) }{2 \; m_e } \; \approx \; \frac{ 2 \; m_W^2}{m_e} \qquad \approx 25\;300\;000\;GeV[/math]
Tak ogromnych energii nie jesteśmy w stanie wytworzyć ! Dotychczas uzyskiwane wiązki pozytonów miały energie [math]E \approx 100 \; GeV[/math], projektowane przyszłe akceleratory mogą dostarczyć energii [math]E \approx 1000 - 5000 \; GeV[/math]...
Dla przeciwbieżnych wiązek elektron-pozyton:
- [math] E_{min} \; = \; \frac{1}{2}\sqrt{s_{min}} \; = \; \frac{1}{2}\sqrt{\left(\sum_i m_i\right)^2} \; = \; \frac{1}{2}\sum_i m_i \; = \; m_W \qquad \approx 80\;GeV[/math]
Takie energie to już nie problem (uzyskiwane były w akceleratorze LEP)...
![Produkcja kwarków w zderzeniu [math]e^+ e^-[/math]](/edu/images/4/45/Ee_gamma.png)
![Produkcja cząstki [math]J/\Psi[/math] w zderzeniu [math]e^+ e^-[/math]](/edu/images/b/be/Ee_jpsi.png)