Matematyka 1 OO/Funkcje elementarne dwóch zmiennych rzeczywistych
Zadanie
Badamy kształt powierzchni zadanej wzorem [math]z=f(x,y)[/math], gdzie
- [math] f(x,y)=x^2+2xy-3y^2 [/math]
W tym celu znajdziemy miejsca zerowe i inne poziomice funkcji [math]f(x,y)[/math] oraz zbadamy kształt przekrojów badanej powierzchni dla ustalonych wartości jednego z agumentów.
Miejsca zerowe
- [math] x^2+2xy-3y^2=0 [/math]
Rozwiązujemy równanie kwadratowe dla zmiennej [math]y[/math] w celu znalezienia równania krzywych, na których [math]f(x,y)=0[/math]
- [math] \Delta _y = 4x^2 + 12 x^2 = 16 x^2 = (4x)^2 [/math]
- [math] y_{1,2}=\frac{-2x\pm \sqrt{(4x)^2}}{-6} = \frac{1}{3}x\mp \frac{2}{3}|x| [/math]
Wyrażenie na każde z rozwiązań, [math]y_1[/math] i [math]y_2[/math], zawiera wartość bezwzględną [math]|x|[/math]. Zapisujemy je w formie wyrażeń bez wartości bezwzględnej, ale z rozbiciem na przedziały
- [math] y_1(x) = \frac{1}{3}x+\frac{2}{3}|x| = \left\lbrace \begin{array}{lcl} \frac{1}{3}x+\frac{2}{3}x=x & dla & x\gt 0 \\ \frac{1}{3}x-\frac{2}{3}x=-\frac{1}{3}x & dla & x\lt 0 \end{array} \right. [/math]
- [math] y_2(x) = \frac{1}{3}x-\frac{2}{3}|x| = \left\lbrace \begin{array}{lcl} \frac{1}{3}x-\frac{2}{3}x=-\frac{1}{3}x & dla & x\gt 0 \\ \frac{1}{3}x+\frac{2}{3}x=x & dla & x\lt 0 \end{array} \right. [/math]
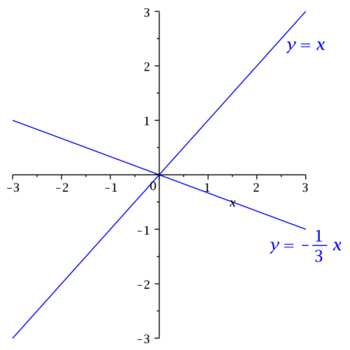
Można obie funkcje [math]y_i(x)[/math] narysować w każdym z przedziałów osobno. Można też zauważyć, że funkcja [math]y_1(x)[/math] dla [math]x\gt 0[/math] razem z funkcją [math]y_2(x)[/math] dla [math]x\lt 0[/math] mają taką samą postać i uzupełniają się do funkcji liniowej [math]y_a(x)=x[/math] na całej osi rzeczywistej. Analogicznie [math]y_1(x)[/math] dla [math]x\lt 0[/math] razem z funkcją [math]y_2(x)[/math] dla [math]x\gt 0[/math] uzupełniają się do funkcji liniowej [math]y_a(x)=-x/3[/math]. Zbiór wszystkich miejsc zerowych funkcji [math]f(x,y)[/math] jest sumą obu linii prostych [math]y=x[/math] i [math]y=-x/3[/math]
Poziomice
Znajdujemy poziomice spełniające równanie [math]f(x,y)=c[/math]. Procedura jest analogiczna do tej użytej do wyznaczenia miejsc zerowych.
- [math] -3y^2+2xy+x^2-c=0 [/math]
- [math] \Delta _y=(2x)^2-4(-3)(x^2-c)=4x^2+12x^2-12c=16x^2-12c=4(4x^2-3c) [/math]
- [math] y_{1,2}=\frac{-2x\pm 2\sqrt{4x^2-3c}}{-6} = \frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2-3c} [/math]
Na tych zajęciach nie pojawiają się wszystkie krzywe drugiego stopnia, a tylko takie, których osie symetrii są równoległe do osi układu współrzędnych. Studenci nie muszę więc rozpoznawać krzywych opisujących poziomice w naszym zadaniu. Dlatego ograniczymy się do wyznaczenia kilku cech charakterystycznych tych poziomic, żebyśmy mogli je naszkicować. Zaczynamy od przypadku [math]c\lt 0[/math]:
- [math] y_{1,2}=\frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2+3|c|} [/math]
Żadna z tych funkcji nie ma miejsc zerowych. Można to pokazać metodą ad absurdum:
- [math] 0=\frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2+3|c|} [/math]
- [math] 0=x\mp \sqrt{4x^2+3|c|} [/math]
- [math] x=\pm \sqrt{4x^2+3|c|} [/math]
- [math] x^2=4x^2+3|c| [/math]
- [math] -3x^2=3|c| [/math]
- [math] x^2=-|c| [/math]
Oczywiście, nie ma żadnej liczby rzeczywistej spełniającej ten warunek, więc żaden punkt z [math]y=0[/math] nie należy do badanej krzywej. Sprawdzamy, jaka jest minimalna dopuszczalna wartość [math]|y|[/math]. Nie mamy jeszcze do dyspozycji rachunku różniczkowego, więc musimy sobie poradzić inną metodą. Rozwiązujemy równanie opisujące poziomicę (dla [math]c\lt 0[/math])
- [math] -3y^2+2xy+x^2+|c|=0 [/math]
ze względu na zmienną [math]x[/math]:
- [math] \Delta _x=(2y)^2-4(-3y^2+|c|)=4y^2+12y^2-4|c|^2 =4(4y^2-|c|) [/math]
Rozwiązania istnieją, jeśli [math]\Delta _x\ge 0[/math], co daje następujące ograniczenie na [math]y[/math]:
- [math] 4y^2\ge |c| \qquad \Rightarrow \qquad |y|\ge \frac{\sqrt{|c|}}{2} [/math]
Dla takich minimalnych [math]|y|[/math] odpowiednie wartości [math]x[/math] wynoszą
- [math] x=\frac{-2y\pm \sqrt{\Delta _x}}{2}=-y [/math]
Zauważamy jeszcze, że dla bardzo dużych wartości zmiennej [math]|x|\gg |c|[/math]
- [math] y_1(x)=\frac{1}{3}-\frac{2}{3}\sqrt{x^2+\frac{3}{4}|c|}\approx \frac{1}{3}-\frac{2}{3}x=-\frac{1}{3}x [/math]
- [math] y_2(x)=\frac{1}{3}+\frac{2}{3}\sqrt{x^2+\frac{3}{4}|c|}\approx \frac{1}{3}+\frac{2}{3}x=x [/math]
co oznacza, że dla dużych wartości [math]|x|[/math] poziomice dla [math]c\lt 0[/math] zbliżają się (asymptotycznie) do prostych zawierających miejsca zerowe funkcji [math]f(x,y)[/math].
Analiza dla [math]c\gt 0[/math] jest nieco inna. Równania opisujące poziomice [math]f(x,y)=c[/math] mają postać
- [math] y_{3,4}(x)=\frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2-3|c|} [/math]
Obie funkcje mają dziedzinę różną od zbioru liczb rzeczywistych. Wyrażenie pod pierwiastkiem jest nieujemne tylko jeśli [math]4x^2\gt 3|c|[/math], więc dziedziną dla obu funkcji [math]y_i(x)[/math] jest
- [math] x\in \left(-\infty ,-\frac{\sqrt{3|c|}}{2}\right\gt \cup \left\lt \frac{\sqrt{3|c|}}{2},\infty \right) [/math]
Wartości zmiennej [math]y[/math] dla minimalnej wartości [math]|x|[/math] wynoszą:
- [math] y_{3,4}=\frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2-3|c|} =\frac{1}{3}x=\mp \frac{\sqrt{3|c|}}{6} [/math]
Każda z funkcji [math]y_{3,4}(x)[/math] ma jedno miejsce zerowe:
- [math] \frac{1}{3}x\mp \frac{1}{3}\sqrt{4x^2-3|c|}=0 \qquad \qquad \qquad x=\pm \sqrt{4x^2-3|c|} [/math]
- [math] x^2=4x^2-3|c| \qquad \qquad \qquad x^2=|c| \qquad \qquad \qquad x=\pm \sqrt{|c|} [/math]
Podobnie jak w przypadku [math]c\lt 0[/math], wykresy poziomic dla [math]c\gt 0[/math] dążą asymptotycznie do zbioru miejsc zerowych dla bardzo dużych wartości [math]|x|[/math].
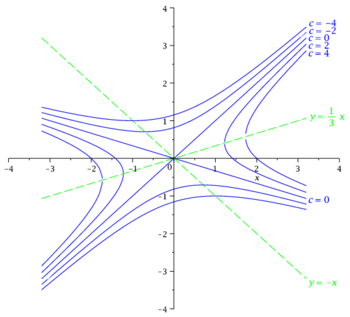
Obliczamy współrzędne charakterystycznych punktów dla kilku wybranych poziomic. Dla [math]c\lt 0[/math] są to przecięcia z osią [math]y[/math] i “wierzchołki” o minimalnej wartości [math]|y|[/math] leżące na prostej [math]y=-x[/math]. Dla [math]c\gt 0[/math] są to przecięcia z osią [math]x[/math] i “wierzchołki” o minimalnej wartości [math]|x|[/math] leżące na prostej [math]y=x/3[/math]. Np. dla [math]c=\pm 2,\pm 4[/math]:
- [math] \begin{array}{|r|c|c|} \hline c & przecięcia z osiami & wierzchołki \\ \hline -4 & \left(0,-\displaystyle \frac{2\sqrt{3}}{3}\right) i \left(0,\displaystyle \frac{2\sqrt{3}}{3}\right) & (-1,1) i (1,-1) \\ \hline -2 & \left(0,-\displaystyle \frac{\sqrt{6}}{3}\right) i \left(0,\displaystyle \frac{\sqrt{6}}{3}\right) & \left(-\displaystyle \frac{\sqrt{2}}{2}, \displaystyle \frac{\sqrt{2}}{2}\right) i \left(\displaystyle \frac{\sqrt{2}}{2}, -\displaystyle \frac{\sqrt{2}}{2}\right) \\ \hline 2 & (-\sqrt{2},0) i (\sqrt{2},0) & \left(-\displaystyle \frac{\sqrt{6}}{2}, \displaystyle \frac{\sqrt{6}}{6}\right) i \left(\displaystyle \frac{\sqrt{6}}{2}, -\displaystyle \frac{\sqrt{6}}{6}\right) \\ \hline 4 & (-2,0) i (2,0) & \left(-\sqrt{3},\displaystyle \frac{\sqrt{3}}{3}\right) i \left(\sqrt{3},-\displaystyle \frac{\sqrt{3}}{3}\right) \\ \hline \end{array} [/math]
Zebrane informacje pozwalają naszkicować wykresy poziomic funkcji [math]f(x,y)[/math].
Kształt powierzchni
Nie każdy potrafi wyobrazić sobie kształt powierzchni na podstawie układu poziomic. Dlatego warto jeszcze wyznaczyć kształt kilku przekrojów powierzchni [math]z=f(x,y)[/math], najprościej w płaszczyznach o stałym [math]x[/math] lub [math]y[/math].
Zacznijmy od płaszczyzny [math]y=y_0={\rm const}[/math]. Wyznaczmy postać funkcji [math]z=g_{y_0}(x)=f(x,y_0)[/math]:
- [math] g_{y_0}(y)=x^2+2y_0x-3y_0^2 [/math]
Jest to parabola z ramionami skierowanymi do góry. Studenci powinni znać podstawową charakterystykę wykresu funkcji kwadratowej postaci [math]ax^2+bx+c[/math]:
- położenie miejsc zerowych, [math]x=(-b\pm \sqrt{b^2-4ac})/(2a)[/math];
- współrzędne wierzchołka, [math](-b/(2a),c-b^2/(4a))[/math].
To ostatnie można łatwo zaleźć przekształcając odpowiednio postać zadanej funkcji kwadratowej:
[math]\begin{matrix} ax^2+bx+c &&\!\!\!\!\!\!\!\! = a(x^2+\frac{b}{a}x)+c = a\left(x^2+2\frac{b}{2a}x +\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2\right)+c \\ &&\!\!\!\!\!\!\!\! = a\left(x+\frac{b}{2a}\right)^2+c-\frac{b^2}{4a} \end{matrix}[/math]
W przypadku rozważanej funkcji [math]g_{y_0}(x)[/math], wierzchołek (minimum) znajduje się w punkcie [math]x=-y_0[/math], a wartość funkcji wynosi [math]z=-4y_0^2[/math].
Kształt przekroju w płaszczyźnie [math]x=x_0[/math] opisuje funkcja [math]z=h_{x_0}(y)=f(x_0,y)[/math]:
- [math] h_{x_0}(y)=-3y^3+2x_0y+x_0^2 [/math]
Jest to parabola z ramionami skierowanymi do dołu. Ma ona maksimum równe [math]z=4x_0^2/3[/math] w punkcie [math]y=x_0/3[/math].
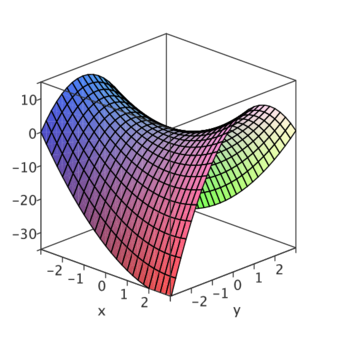
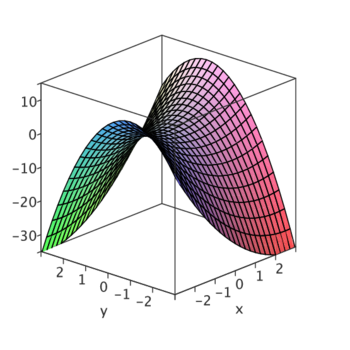
Połączenie informacji na temat poziomic i kształtu przekrojów powinno pozwolić na dość dokładne opisanie kształtu powierzchni zadanej równaniem [math]z=f(x,y)[/math].
wykres 3D
Jeśli jest taka możliwość, warto pokazać studentom wydruk z programu rysującego wykresy funkcji od dwóch zmiennych (Maple lub Mathematica). Jeszcze lepsze byłoby zaprezentowanie takiego wykresu w działającym programie - i skorzystanie np. z możliwości obracania otrzymanej powierzchni.
Krzywe stożkowe
Przypominamy ogólne wzory na krzywe stożkowe. Ograniczamy się do prostych przypadków, gdy osie symetrii są równoległe do osi układu współrzędnych. Takie krzywe są zbiorem miejsc zerowych następujących wielomianów drugiego stopnia dwóch zmiennych:
- okrąg: [math]\qquad (x-x_0)^2+(y-y_0)^2=R^2[/math]
- parabola: [math]\qquad y=a(x-x_0)^2+y_0\quad [/math] lub [math]\quad x=a(y-y_0)^2+x_0[/math]
- elipsa: [math]\qquad \displaystyle \frac{(x-x_0)^2}{a^2}+\displaystyle \frac{(y-y_0)^2}{b^2}=1[/math]
- hiperbola: [math]\qquad \displaystyle \frac{(x-x_0)^2}{a^2}\displaystyle -\frac{(y-y_0)^2}{b^2}=1 \quad [/math] lub [math]\quad \displaystyle \frac{(x-x_0)^2}{a^2}-\displaystyle \frac{(y-y_0)^2}{b^2}=-1[/math]
Ilustrujemy to kilkoma przykładami.
Zadanie
Na jakiej krzywej leżą miejsca zerowe funkcji [math]f(x,y)=x^2+y^2+4x-2y-4[/math]?
- [math] x^2+y^2+4x-2y-4=0 [/math]
- [math] (x^2+4x+4-4)+(y^2-2y+1-1)=4 [/math]
- [math] (x+2)^2-4+(y-1)^2-1=4 [/math]
- [math] (x+2)^2+(y-1)^2=3^2 [/math]
To jest okrąg o środku w punkcie o współrzędnych [math](-2,1)[/math] i promieniu równym 3.
Zadanie
Na jakiej krzywej leżą miejsca zerowe funkcji [math]f(x,y)=4x^2-16x-y^2[/math]?
- [math] 4x^2-16x-y^2=0 [/math]
- [math] 4(x^2-4x+4-4)-y^2=0 [/math]
- [math] 4(x-2)^2-16-y^2=0 [/math]
- [math] \frac{(x-2)^2}{2^2}-\frac{y^2}{4^2}=1 [/math]
Jest to hiperbola o “środku” w punkcie [math](2,0)[/math]. Co oznacza w tym przypadku “środek”? Jest to punkt, w którym przecinają się proste będące asymptotami tej hiperboli. Asymptoty znajdujemy rozpatrując granicę bardzo dużych wartości [math]|x|[/math] i [math]|y|[/math]. W tej granicy pomijamy 1 po prawej stronie ostatniego równania oraz 2 w porównaniu z [math]x[/math]. Dostajemy równanie
- [math] \frac{x^2}{2^2}-\frac{y^2}{4^2}\approx 0 [/math]
- [math] y^2\approx 4x^2 [/math]
- [math] y\approx \pm 2x [/math]
Asymptoty przechodzą przez punkt [math](2,0)[/math], więc ich dokładne równanie ma postać:
- [math] y=\pm (x-2) [/math]
Badana hiperbola ma miejsca wspólne z osią [math]y[/math]:
- [math] \frac{(x-2)^2}{2^2}=1 [/math]
- [math] x-2=\pm 2 [/math]
- [math] x_1=0 \qquad x_2=4 [/math]
Szkicujemy wykres tej hiperboli