Matematyka 1 OO/Sumy szeregów liczbowych
Zadanie
Udowodnić, że suma szeregu
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \frac{4(-1)^{n+1}}{2n-1} [/math]
jest skończona.
Rozbijamy sumę [math]S[/math] na sumę częściową [math]2k[/math] pierwszych wyrazów, [math]S_{2k}[/math] i sumę pozostałych (nieskończenie wielu) wyrazów
[math]\begin{matrix} S &&\!\!\!\!\!\!\!\!= S_{2k} + \sum _{n=2k+1}^\infty \frac{4(-1)^{n+1}}{2n-1} \\&&\!\!\!\!\!\!\!\!= S_{2k} +4\left[\frac{(-1)^{2k+1+1}}{2(2k+1)-1}+\frac{(-1)^{2k+2+1}}{2(2k+2)-1} +\frac{(-1)^{2k+3+1}}{2(2k+3)-1}+\frac{(-1)^{2k+4+1}}{2(2k+4)-1} +\ldots \right] \\&&\!\!\!\!\!\!\!\!= S_{2k} +4\left[\frac{1}{4k+1}-\frac{1}{4k+3}+\frac{1}{4k+5}-\frac{1}{4k+7} +\ldots \right] \\&&\!\!\!\!\!\!\!\!= S_{2k} +4\left[\frac{2}{(4k+1)(4k+3)}+\frac{2}{(4k+5)(4k+7)} +\ldots \right] \end{matrix}[/math]
Każdy z ułamków w nawiasie kwadratowym jest dodatni, więc dostajemy nierówność
- [math] S \gt S_{2k} [/math]
Teraz rozbijamy sumę [math]S[/math] na sumę częściową [math]S_{2k+1}[/math] pierwszych [math](2k+1)[/math] wyrazów i sumę pozostałych (nieskończenie wielu) wyrazów
[math]\begin{matrix} S &&\!\!\!\!\!\!\!\!= S_{2k+1} + \sum _{n=2k+2}^\infty \frac{4(-1)^{n+1}}{2n-1} \\&&\!\!\!\!\!\!\!\!= S_{2k+1} +4\left[\frac{(-1)^{2k+2+1}}{2(2k+2)-1}+\frac{(-1)^{2k+3+1}}{2(2k+3)-1} +\frac{(-1)^{2k+4+1}}{2(2k+4)-1}+\frac{(-1)^{2k+5+1}}{2(2k+5)-1} +\ldots \right] \\&&\!\!\!\!\!\!\!\!= S_{2k+1} +4\left[-\frac{1}{4k+3}+\frac{1}{4k+5}-\frac{1}{4k+7}+\frac{1}{4k+9} +\ldots \right] \\&&\!\!\!\!\!\!\!\!= S_{2k+1} +4\left[\frac{-2}{(4k+3)(4k+5)}+\frac{-2}{(4k+7)(4k+9)} +\ldots \right] \end{matrix}[/math]
Każdy z ułamków w nawiasie kwadratowym jest ujemny, więc dostajemy nierówność
- [math] S \lt S_{2k+1} [/math]
Obie nierówności razem dają dolne i górne ograniczenie na sumę [math]S[/math]:
- [math] S_{2k} \lt S \lt S_{2k+1} [/math]
Obliczamy różnicę wartości tych ograniczeń
- [math] S_{2k+1} - S_{2k} = a_{2k+1} = \frac{4(-1)^{2k+2}}{4k+2-1} = \frac{4}{4k+1} [/math]
Obliczamy granicę wartości tej różnicy dla [math]k\rightarrow \infty [/math]
- [math] \lim _{k\rightarrow \infty } \left(S_{2k+1} - S_{2k}\right) = \lim _{k\rightarrow \infty } \frac{4}{4k+1} = 0 [/math]
Następnie wykazujemy monotoniczność ciągu parzystych sum cząstkowych
[math]\begin{matrix} S_{2k+2} - S_{2k} = a_{2k+1}+a_{2k+2} &&\!\!\!\!\!\!\!\! = \frac{4(-1)^{2k+2}}{2(2k+1)-1} + \frac{4(-1)^{2k+3}}{2(2k+2)-1} \\ &&\!\!\!\!\!\!\!\! = \frac{4}{4k+1} - \frac{4}{4k+3} = \frac{8}{(4k+1)(4k+3)} \gt 0 \end{matrix}[/math]
Ten ciąg jest ściśle rosnący. Analogicznie pokazujemy, że ciąg nieparzystych sum cząstkowych jest ciągiem ściśle malejący:
[math]\begin{matrix} S_{2k+3} - S_{2k+1} = a_{2k+2}+a_{2k+3} &&\!\!\!\!\!\!\!\! = \frac{4(-1)^{2k+3}}{2(2k+2)-1} + \frac{4(-1)^{2k+4}}{2(2k+3)-1} \\ &&\!\!\!\!\!\!\!\! = -\frac{4}{4k+3} + \frac{4}{4k+5} = -\frac{8}{(4k+3)(4k+5)} \lt 0 \end{matrix}[/math]
Udowodniliśmy, że liczba [math]S[/math] spełnia następujące warunki:
- [math]S[/math] jest większe od każdego wyrazu rosnącego ciągu parzystych sum cząstkowych [math]S_{2k}[/math]
- [math]S[/math] jest mniejsze od każdego wyrazu malejącego ciągu nieparzystych sum cząstkowych [math]S_{2k+1}[/math]
- ciąg różnic między wartościami wyrazów tych monotonicznych ciągów, [math]S_{2k+1}-S_{2k}[/math], ma granicę równą zero
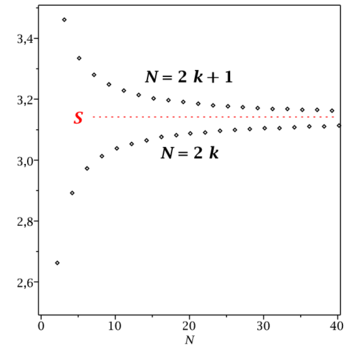
Powyższe warunki można zilustrować odpowiednim wykresem
Pokazują one, że szereg
[math]S=\sum _{n=1}^\infty a_{n}[/math] jest zbieżny.
Na obecnym etapie zajęć nie możemy jeszcze obliczyć wartości liczbowej sumy [math]S[/math]. Warto jednak wypisać przybliżone wartości kilku sum cząstkowych
| [math]N[/math] | [math]S_N[/math] | [math]N[/math] | [math]S_N[/math] |
| 2 | 2.667 | 3 | 3.4467 |
| 4 | 2.895 | 5 | 3.340 |
| 6 | 2.976 | 7 | 3.284 |
| 20 | 3.092 | 21 | 3.189 |
| 50 | 3.122 | 51 | 3.161 |
| 100 | 3.13159 | 101 | 3.15149 |
| 1000 | 3.14059 | 1001 | 3.14259 |
Sumą szeregu jest liczba [math]\pi [/math], ale, jak widać w powyższej tabelce,
ciąg sum cząstkowych zbiega dość powoli. Obliczona wcześniej
różnica [math]S_{2N+1}-S_{2N}=4/(4N+1)[/math] pokazuje, że suma cząstkowa
[math]S_k[/math] przybliża [math]S[/math] z dokładnością rzędu [math]1/k[/math] (to też można
dostrzec w tabelce).
Zadanie
Znaleźć sumę szeregu
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \frac{1}{n(n+1)} [/math]
Zadanie bardzo łatwo rozwiązać po zapisaniu wyrazu [math]a_n[/math] w postaci kombinacji funkcji wymiernych o mianownikach liniowych w [math]n[/math] (operacja odwrotna do sprowadzania do wspólnego mianownika):
- [math] a_n = \frac{1}{n(n+1)} = \frac{b}{n} + \frac{c}{n+1} = \frac{b(n+1)+cn}{n(n+1)} = \frac{b+(b+c)n}{n(n+1)} [/math]
Licznik ostatniego ułamka ma być równy 1, więc otrzymujemy układ równań
- [math] \left\lbrace \begin{array}{r} b=1 \\ b+c=0 \end{array} \right. [/math]
którego rozwiązanie ma postać [math]b=1[/math], [math]c=-1[/math]. Szukaną sumę szeregu zapisujemy w postaci
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \left(\frac{1}{n}-\frac{1}{n+1}\right) [/math]
Obliczamy kilka pierwszych sum cząstkowych
[math]\begin{matrix} S_1 &&\!\!\!\!\!\!\!\! = 1-\frac{1}{2}=\frac{1}{2} \\ S_2 &&\!\!\!\!\!\!\!\! = \left(1-\frac{1}{2}\right) + \left(\frac{1}{2}-\frac{1}{3}\right)=1-\frac{1}{3}=\frac{2}{3} \\ S_3 &&\!\!\!\!\!\!\!\! = \left(1-\frac{1}{2}\right) + \left(\frac{1}{2}-\frac{1}{3}\right) + \left(\frac{1}{3}-\frac{1}{4}\right) =1-\frac{1}{4}=\frac{3}{4} \end{matrix}[/math]
Łatwo zauważyć, że [math]N[/math]-ta suma cząstkowa wynosi
- [math] S_N = \left(1-\frac{1}{2}\right) + \ldots + \left(\frac{1}{N}-\frac{1}{N+1}\right) =1-\frac{1}{N+1}=\frac{N}{N+1} [/math]
co pozwala obliczyć sumę [math]S[/math] jako granicę ciągu sum cząstkowych
- [math] S = \lim _{N\rightarrow \infty } S_N = \lim _{N\rightarrow \infty } \frac{N}{N+1} = 1 [/math]
Zadanie
Udowodnić zbieżność szeregu
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \frac{1}{n^c} [/math]
dla [math]c\gt 1[/math]. Dokonujemy następujących operacji w celu znalezienia ograniczenia na ciąg sum cząstkowych:
[math]\begin{matrix} S_N &&\!\!\!\!\!\!\!\! = 1+\frac{1}{2^c}+\frac{1}{3^c} + \ldots + \frac{1}{N^c} \lt 1+\frac{1}{2^c}+\frac{1}{3^c} + \ldots + \frac{1}{N^c} + \ldots + \frac{1}{(2N)^c} + \frac{1}{(2N+1)^c} \\ &&\!\!\!\!\!\!\!\! = 1 +\left(\frac{1}{2^c}+\frac{1}{3^c}\right) +\ldots + \left(\frac{1}{(2k)^c}+\frac{1}{(2k+1)^c}\right) +\ldots + \left(\frac{1}{(2N)^c}+\frac{1}{(2N+1)^c}\right) \end{matrix}[/math]
Wyrażenia w nawiasach spełniają warunek
- [math] \left(\frac{1}{(2k)^c}+\frac{1}{(2k+1)^c}\right) \lt \left(\frac{1}{(2k)^c}+\frac{1}{(2k)^c}\right) = \frac{2}{(2k)^c} [/math]
[math]N[/math]-ta suma cząstkowa spełnia więc nierówność
[math]\begin{matrix} S_N &&\!\!\!\!\!\!\!\! \lt 1 + \frac{2}{2^c} +\ldots + \frac{2}{(2k)^c} +\ldots + \frac{2}{(2N)^c} = 1 + \frac{1}{2^{c-1}} +\ldots + \frac{1}{2^{c-1}}\,\frac{1}{k^c} +\ldots + \frac{1}{2^{c-1}}\,\frac{1}{N^c} \\ &&\!\!\!\!\!\!\!\! = 1 + \frac{1}{2^{c-1}}\left(1+\ldots +\frac{1}{k^c}+\ldots +\frac{1}{N^c} \right) = 1 + \frac{1}{2^{c-1}}\,S_N \end{matrix}[/math]
Porównując skrajne wyrażenia w powyższym wzorze, dostajemy
- [math] \left(1-\frac{1}{2^{c-1}}\right)S_N \lt 1 [/math]
Wyrażenie w nawiasie jest liczba dodatnią (co udowodnimy za chwilę), więc możemy powyższą nierównośc przekształcic do postaci
- [math] S_N \lt \frac{1}{1-\displaystyle \frac{1}{2^{c-1}}} [/math]
Prawa strona tej nierówności jest dla każdego [math]c\gt 1[/math] skończoną liczbą dodatnią, co pokazuje następujący ciąg nierówności
[math]\begin{matrix} \infty \gt c\gt 1 &&\!\!\!\!\!\!\!\!\qquad \Rightarrow \qquad \infty \gt 2^c\gt 2 \qquad \Rightarrow \qquad \infty \gt \frac{2^c}{2}\gt 1 \qquad \Rightarrow \qquad \infty \gt 2^{c-1}\gt 1 \\&&\!\!\!\!\!\!\!\!\qquad \Rightarrow \qquad 0\lt \frac{1}{2^{c-1}}\lt 1 \qquad \Rightarrow \qquad 1\gt 1-\displaystyle \frac{1}{2^{c-1}}\gt 0 \end{matrix}[/math]
O ciągu sum cząstkowych wiemy więc, że
- jest ciągiem rosnącym (ponieważ [math]S_{N+1}-S_N=1/(N+1)\gt 0[/math])
- jest ciągiem ograniczonym z góry przez ustaloną dla każdego [math]c[/math] skończoną liczbę dodatnią
Ciąg [math]S_N[/math], jako rosnący i ograniczony z góry, jest ciągiem zbieżnym, co należało wykazać.
Zadanie
Znaleźć sumę szeregu
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \frac{1}{4n^2-1} [/math]
Warto wypisać jawnie kilka pierwszych wyrazów tej sumy
- [math] \sum _{n=1}^\infty \frac{1}{4n^2-1} = \sum _{n=1}^\infty \frac{1}{(2n-1)(2n+1)} = \frac{1}{1\cdot 3}+\frac{1}{3\cdot 5}+\frac{1}{5\cdot 7} +\frac{1}{7\cdot 9}+\ldots [/math]
Suma cząstkowa [math]S_N[/math] jest równa
- [math] S_N = \frac{1}{1\cdot 3}+\ldots +\frac{1}{(2k-1)(2k+1)} +\cdots +\frac{1}{(2N-1)(2N+1)} [/math]
Każdy wyraz powyższej sumy zapisujemy jako kombinację prostych funkcji wymiernych
- [math] \frac{1}{(2k-1)(2k+1)} = \frac{b}{2k-1}+\frac{c}{2k+1} = \frac{b(2k+1)+c(2k-1)}{(2k-1)(2k+1)} = \frac{2(b+c)k+(b-c)}{(2k-1)(2k+1)} [/math]
co prowadzi do układu równań
- [math] \left\lbrace \begin{array}{r} b-c=1\\ 2(b+c)=0\\ \end{array} \right. [/math]
którego rozwiązaniem jest [math]b=\frac{1}{2}[/math], [math]c=-\frac{1}{2}[/math]. [math]N[/math]-tą sumę cząstkową możemy więc zapisać w postaci
[math]\begin{matrix} S_N &&\!\!\!\!\!\!\!\! = \left(\frac{1}{2}\cdot 1-\frac{1}{2}\cdot \frac{1}{3}\right) + \left(\frac{1}{2}\cdot \frac{1}{3}-\frac{1}{2}\cdot \frac{1}{5}\right) +\ldots + \left(\frac{1}{2}\cdot \frac{1}{2k-1}-\frac{1}{2}\cdot \frac{1}{2k+1}\right) \\ && + \left(\frac{1}{2}\cdot \frac{1}{2k+1}-\frac{1}{2}\cdot \frac{1}{2k+3}\right) +\ldots + \left(\frac{1}{2}\cdot \frac{1}{2N-1}-\frac{1}{2}\cdot \frac{1}{2N+1}\right) \\ &&\!\!\!\!\!\!\!\! = \frac{1}{2} \left[\left(1-\frac{1}{3}\right) + \left(\frac{1}{3}-\frac{1}{5}\right) +\ldots + \left(\frac{1}{2k-1}-\frac{1}{2k+1}\right) + \left(\frac{1}{2k+1}-\frac{1}{2k+3}\right)\right. \\ &&\quad \left. +\ldots + \left(\frac{1}{2N-1}-\frac{1}{2N+1}\right)\right] \\ &&\!\!\!\!\!\!\!\! = \frac{1}{2} \left[1-\frac{1}{2N+1}\right] \end{matrix}[/math]
Teraz łatwo możemy już obliczyć sumę szeregu jako granicę ciągu sum cząstkowych
- [math] S = \lim _{N\rightarrow \infty } S_N = \lim _{N\rightarrow \infty } \frac{1}{2}\left(1-\frac{1}{2N+1}\right)=\frac{1}{2} [/math]
Zadanie
Znaleźć sumę szeregu
- [math] S=\sum _{n=1}^\infty a_{n} =\sum _{n=1}^\infty \frac{1}{(4n)^2-1} [/math]
korzystając z wyniku podanego przy rozwiązywaniu zadania 4.1:
- [math] 4\sum _{n=1}^{\infty }\frac{(-1)^{n+1}}{2n-1}=\pi [/math]
Wypisujemy jawnie kilka pierwszych wyrazów sumy
- [math] \sum _{n=1}^\infty \frac{1}{16n^2-1} = \sum _{n=1}^\infty \frac{1}{(4n-1)(4n+1)} = \frac{1}{3\cdot 5}+\frac{1}{7\cdot 9}+\frac{1}{11\cdot 13} +\frac{1}{15\cdot 17}+\ldots [/math]
Podobnie jak w poprzednich zadaniach, zapisujemy [math]n[/math]-ty wyraz szeregu w innej postaci
- [math] a_n = \frac{1}{(4n-1)(4n+1)} = \frac{b}{4n-1}+\frac{c}{4n+1} = \frac{4(b+c)n+(b-c)}{(4n-1)(4n+1)} [/math]
co, po wyznaczeniu stałych [math]b[/math] i [math]c[/math], daje
- [math] a_n = \frac{1}{2}\left(\frac{1}{4n-1}-\frac{1}{4n+1}\right) [/math]
Sumę szeregu można zapisać w postaci
- [math] S = \sum _{n=1}^\infty \frac{1}{2}\left(\frac{1}{4n-1}-\frac{1}{4n+1}\right) = \frac{1}{2}\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\frac{1}{11}-\frac{1}{13} +\ldots \right) [/math]
Tym razem nie ma żadnego kasowania między składnikami kolejnych wyrazów szeregu [math]a_n[/math] i [math]a_{n+1}[/math]. Szereg w nawiasie w powyższym równaniu jest podobny do szeregu z sumą równą [math]\pi [/math] podanego w treści zadania
- [math] \pi = 4\sum _{n=1}^{\infty }\frac{(-1)^{n+1}}{2n-1} = 4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\ldots \right) [/math]
Aby z tego skorzystać, zmieniamy ostatnio uzyskaną postać wyrażenia na sumę [math]S[/math]:
[math]\begin{matrix} S &&\!\!\!\!\!\!\!\! = \frac{1}{2}\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\frac{1}{11} +\ldots \right) = \frac{1}{2}\left(1-1+\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\frac{1}{11} +\ldots \right) \\ &&\!\!\!\!\!\!\!\! = \frac{1}{2}\left[1-\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11} +\ldots \right)\right] = \frac{1}{2}\left[1-\left(\frac{\pi }{4}\right)\right] \\ &&\!\!\!\!\!\!\!\! = \frac{1}{2} - \frac{\pi }{8} \end{matrix}[/math]