Obrazowanie:Obrazowanie Medyczne/Podstawy Rekonstrukcji Obrazów Tomograficznych: Różnice pomiędzy wersjami
(Utworzono nową stronę " ==Wstęp== File:projekcja_1.png|300px|thumb|right|<figure id="fig:projekcja_1"></figure>Badany obiekt składa się z dwóch struktur (szare koła). Dokonajmy rzutowa...") |
|||
| Linia 12: | Linia 12: | ||
===Podstawy Matematyczne — Delta Diraca=== | ===Podstawy Matematyczne — Delta Diraca=== | ||
Poprawne zrozumienie Twierdzenia Radona wymaga opanowania pewnych zagadnień matematycznych, które przypomnimy w poniższym podrozdziale. | Poprawne zrozumienie Twierdzenia Radona wymaga opanowania pewnych zagadnień matematycznych, które przypomnimy w poniższym podrozdziale. | ||
| − | <equation><math> | + | <equation id="1"><math> |
\delta(x)=\left\{ | \delta(x)=\left\{ | ||
\begin{array}{lcr} | \begin{array}{lcr} | ||
| Linia 22: | Linia 22: | ||
A.<br> | A.<br> | ||
| − | <equation><math> | + | <equation id="2"><math> |
\delta(x-b)=\left\{ | \delta(x-b)=\left\{ | ||
\begin{array}{lcr} | \begin{array}{lcr} | ||
| Linia 32: | Linia 32: | ||
B.<br> | B.<br> | ||
| − | <equation><math> | + | <equation id="3"><math> |
\int_{-\infty}^{\infty}\delta(x)dx = 1 | \int_{-\infty}^{\infty}\delta(x)dx = 1 | ||
</math></equation> | </math></equation> | ||
| Linia 38: | Linia 38: | ||
C.<br> | C.<br> | ||
| − | <equation><math> | + | <equation id="4"><math> |
\delta (-x) = \delta (x) | \delta (-x) = \delta (x) | ||
</math></equation> | </math></equation> | ||
| Linia 44: | Linia 44: | ||
D.<br> | D.<br> | ||
| − | <equation><math> | + | <equation id="5"><math> |
\delta (ax) = \frac{1}{|a|}\delta(x) | \delta (ax) = \frac{1}{|a|}\delta(x) | ||
</math></equation> | </math></equation> | ||
| Linia 50: | Linia 50: | ||
E.<br> | E.<br> | ||
| − | <equation><math> | + | <equation id="6"><math> |
\int_{-\infty}^{\infty} g(x)\delta(x)dx = g(0) | \int_{-\infty}^{\infty} g(x)\delta(x)dx = g(0) | ||
</math></equation> | </math></equation> | ||
| Linia 56: | Linia 56: | ||
F.<br> | F.<br> | ||
| − | <equation><math> | + | <equation id="7"><math> |
\int_{-\infty}^{\infty} g(x-b)\delta(x)dx = g(b) | \int_{-\infty}^{\infty} g(x-b)\delta(x)dx = g(b) | ||
</math></equation> | </math></equation> | ||
| Linia 64: | Linia 64: | ||
G.<br> | G.<br> | ||
| − | <equation><math> | + | <equation id="8"><math> |
\int_{-\infty}^{\infty}\delta(x-a)\delta(x-b)dx = \delta(a-b) | \int_{-\infty}^{\infty}\delta(x-a)\delta(x-b)dx = \delta(a-b) | ||
</math></equation> | </math></equation> | ||
Dowód:<br> | Dowód:<br> | ||
| − | <equation><math> | + | <equation id="9"><math> |
\begin{array}{l} | \begin{array}{l} | ||
x-b=x' \\ | x-b=x' \\ | ||
| Linia 82: | Linia 82: | ||
H.<br> | H.<br> | ||
| − | <equation><math> | + | <equation id="10"><math> |
\delta(ax+b)=\frac{1}{|a|}\delta(x+\frac{b}{a}) | \delta(ax+b)=\frac{1}{|a|}\delta(x+\frac{b}{a}) | ||
</math></equation> | </math></equation> | ||
| Linia 93: | Linia 93: | ||
I.<br> | I.<br> | ||
| − | <equation><math> | + | <equation id="11"><math> |
\int_{-\infty}^{\infty} g(x)\delta(ax+b)dx=\frac{1}{|a|}\delta(-\frac{b}{a}) | \int_{-\infty}^{\infty} g(x)\delta(ax+b)dx=\frac{1}{|a|}\delta(-\frac{b}{a}) | ||
</math></equation> | </math></equation> | ||
| Linia 122: | Linia 122: | ||
Transformata Radona to transformata całkowa o następującej postaci: | Transformata Radona to transformata całkowa o następującej postaci: | ||
| − | <equation><math> | + | <equation id="12"><math> |
G(a,b)=\int_{-\infty}^{\infty} g(x,y)\delta(ax+b)dx | G(a,b)=\int_{-\infty}^{\infty} g(x,y)\delta(ax+b)dx | ||
</math></equation> | </math></equation> | ||
| Linia 130: | Linia 130: | ||
Dowód:<br> | Dowód:<br> | ||
Niech będzie dana funkcja <math>h(x,y)</math>, będąca kombinacją liniową funkcji <math>g_i(x,y)</math>: | Niech będzie dana funkcja <math>h(x,y)</math>, będąca kombinacją liniową funkcji <math>g_i(x,y)</math>: | ||
| − | <equation><math> | + | <equation id="13"><math> |
h(x,y) = \sum_{i}w_{i}g_{i}(x,y) | h(x,y) = \sum_{i}w_{i}g_{i}(x,y) | ||
</math></equation> | </math></equation> | ||
Wtedy jej transformata Radona <math>h(x,y)</math> wynosi: | Wtedy jej transformata Radona <math>h(x,y)</math> wynosi: | ||
| − | <equation><math> | + | <equation id="14"><math> |
H(a,b) = \sum_{i}\int_{-\infty}^{\infty} g_{i}(x,y)dx = \sum_{i}w_{i}h_{i}(a,b) | H(a,b) = \sum_{i}\int_{-\infty}^{\infty} g_{i}(x,y)dx = \sum_{i}w_{i}h_{i}(a,b) | ||
</math></equation> | </math></equation> | ||
| Linia 140: | Linia 140: | ||
B. Transformata Radona funkcji przesuniętej do współrzędnych <math>(x_0,y_0)</math> <br> | B. Transformata Radona funkcji przesuniętej do współrzędnych <math>(x_0,y_0)</math> <br> | ||
| − | <equation><math> | + | <equation id="15"><math> |
\begin{array}{l} | \begin{array}{l} | ||
h(x,y) = g(x-x_0,y-y_0) \\ | h(x,y) = g(x-x_0,y-y_0) \\ | ||
| Linia 148: | Linia 148: | ||
</math></equation> | </math></equation> | ||
Dokonując zamiany zmiennych: | Dokonując zamiany zmiennych: | ||
| − | <equation><math> | + | <equation id="16"><math> |
\begin{array}{l} | \begin{array}{l} | ||
x-x_0=x' \\ | x-x_0=x' \\ | ||
| Linia 160: | Linia 160: | ||
dostajemy: | dostajemy: | ||
| − | <equation><math> | + | <equation id="17"><math> |
H(a,b) = \int_{-\infty}^{\infty} g(x',ax_0+b+y_0)dx | H(a,b) = \int_{-\infty}^{\infty} g(x',ax_0+b+y_0)dx | ||
</math></equation> | </math></equation> | ||
suma wyrażeń: <math>kx_0+b-y_0</math> jest pewną stałą, będącą nowym współczynnikiem przesunięcia prostej względem początku układu współrzędnych, wzdłuż której następuje całkowanie funkcji Ostatecznie dostajemy następujący wynik. Jeżeli transformata Radona funkcji <math>g(x,y)</math> wynosi <math>G(a,b)</math>, to transformata Radona funkcji <math>g(x-x_0,y-y_0)</math> jest równa: | suma wyrażeń: <math>kx_0+b-y_0</math> jest pewną stałą, będącą nowym współczynnikiem przesunięcia prostej względem początku układu współrzędnych, wzdłuż której następuje całkowanie funkcji Ostatecznie dostajemy następujący wynik. Jeżeli transformata Radona funkcji <math>g(x,y)</math> wynosi <math>G(a,b)</math>, to transformata Radona funkcji <math>g(x-x_0,y-y_0)</math> jest równa: | ||
| − | <equation><math> | + | <equation id="18"><math> |
H(a,b) = G(a,ax_0+b-y_0) | H(a,b) = G(a,ax_0+b-y_0) | ||
</math></equation> | </math></equation> | ||
| Linia 174: | Linia 174: | ||
Zakładamy, że punkt ma nieskończenie wielką amplitudę. Taki punkt możemy zamodelować za pomocą Delty Diraca: | Zakładamy, że punkt ma nieskończenie wielką amplitudę. Taki punkt możemy zamodelować za pomocą Delty Diraca: | ||
| − | <equation><math> | + | <equation id="19"><math> |
g(x,y) = \delta(x)\delta(y) | g(x,y) = \delta(x)\delta(y) | ||
</math></equation> | </math></equation> | ||
co oznacza, że funkcja <math>g(x,y)</math> ma następującą postać: | co oznacza, że funkcja <math>g(x,y)</math> ma następującą postać: | ||
| − | <equation><math> | + | <equation id="20"><math> |
g(x,y)=\left\{ | g(x,y)=\left\{ | ||
\begin{array}{ccccc} | \begin{array}{ccccc} | ||
| Linia 187: | Linia 187: | ||
</math></equation> | </math></equation> | ||
Obliczmy transformatę Radona powyższej funkcji: | Obliczmy transformatę Radona powyższej funkcji: | ||
| − | <equation><math> | + | <equation id="21"><math> |
G(a,b) = \int_{-\infty}^{\infty} g(x,ax+b)dx=\int_{-\infty}^{\infty}\delta(x)\delta(ax+b)dx | G(a,b) = \int_{-\infty}^{\infty} g(x,ax+b)dx=\int_{-\infty}^{\infty}\delta(x)\delta(ax+b)dx | ||
</math></equation> | </math></equation> | ||
Przekształcimy ten wzór, korzystając z właściwości Delty Diraca. | Przekształcimy ten wzór, korzystając z właściwości Delty Diraca. | ||
| − | <equation><math> | + | <equation id="22"><math> |
\begin{array}{l} | \begin{array}{l} | ||
\int_{-\infty}^{\infty}\delta(x)\delta(ax+b)dx=\frac{1}{|a|}\int_{-\infty}^{\infty}\delta(x)\delta(x+\frac{b}{a})dx \\ | \int_{-\infty}^{\infty}\delta(x)\delta(ax+b)dx=\frac{1}{|a|}\int_{-\infty}^{\infty}\delta(x)\delta(x+\frac{b}{a})dx \\ | ||
| Linia 205: | Linia 205: | ||
Ostatecznie otrzymaliśmy zatem następujący wynik: | Ostatecznie otrzymaliśmy zatem następujący wynik: | ||
| − | <equation><math> | + | <equation id="23"><math> |
g(x,y) = \delta(x)(y)\xrightarrow{\textrm{Transfromata Radona}}G(a,b)=\delta(b) | g(x,y) = \delta(x)(y)\xrightarrow{\textrm{Transfromata Radona}}G(a,b)=\delta(b) | ||
</math></equation> | </math></equation> | ||
| Linia 215: | Linia 215: | ||
Jest to bardzo ważny przykład, ponieważ każdy obiekt możemy przedstawić jako sumę punktów o różnych współrzędnych, których amplituda reprezentuje pewną cechę fizyczną obiektu. Wykorzystując dalej liniowość Transformaty Radona, możemy obliczyć Transformatę Radona danego obiektu jako sumę Transformat Radona punktów składających się na ten obiekt. Podobnie jak w poprzednim przykładzie, punkt możemy wyrazić za pomocą Delty Diraca. | Jest to bardzo ważny przykład, ponieważ każdy obiekt możemy przedstawić jako sumę punktów o różnych współrzędnych, których amplituda reprezentuje pewną cechę fizyczną obiektu. Wykorzystując dalej liniowość Transformaty Radona, możemy obliczyć Transformatę Radona danego obiektu jako sumę Transformat Radona punktów składających się na ten obiekt. Podobnie jak w poprzednim przykładzie, punkt możemy wyrazić za pomocą Delty Diraca. | ||
| − | <equation><math> | + | <equation id="24"><math> |
g(x,y) = \delta(x-x_0)\delta(y-y_0) | g(x,y) = \delta(x-x_0)\delta(y-y_0) | ||
</math></equation> | </math></equation> | ||
Postać funkcji <math>g(x,y)</math> jest zatem następująca: | Postać funkcji <math>g(x,y)</math> jest zatem następująca: | ||
| − | <equation><math> | + | <equation id="25"><math> |
g(x,y)=\left\{ | g(x,y)=\left\{ | ||
\begin{array}{ccccc} | \begin{array}{ccccc} | ||
| Linia 232: | Linia 232: | ||
</math> | </math> | ||
a zatem transformata Radona punktu przesuniętego jest równa: | a zatem transformata Radona punktu przesuniętego jest równa: | ||
| − | <equation><math> | + | <equation id="26"><math> |
g(x,y) = \delta(x-x_0)(y-y_0)\xrightarrow{\textrm{Transfromata Radona}}G(a,b)=\delta(ax_0+b-y_0) | g(x,y) = \delta(x-x_0)(y-y_0)\xrightarrow{\textrm{Transfromata Radona}}G(a,b)=\delta(ax_0+b-y_0) | ||
</math></equation> | </math></equation> | ||
| Linia 242: | Linia 242: | ||
Przykład ten podajemy ze względu na jego znaczenie w grafice komputerowej. Uprzedzając wyniki obliczeń podamy, iż Transformata Radona punktu w kartezjańskim układzie współrzędnych prowadzi do punktu we układzie współrzędnych Transformaty Radona. Punkt te ma współrzędne odpowiadające parametrom prostej. W ten sposób można wykorzystać Transformatę Radona do wynajdywanie w obiekcie, czy obrazach linii prostych. <br> | Przykład ten podajemy ze względu na jego znaczenie w grafice komputerowej. Uprzedzając wyniki obliczeń podamy, iż Transformata Radona punktu w kartezjańskim układzie współrzędnych prowadzi do punktu we układzie współrzędnych Transformaty Radona. Punkt te ma współrzędne odpowiadające parametrom prostej. W ten sposób można wykorzystać Transformatę Radona do wynajdywanie w obiekcie, czy obrazach linii prostych. <br> | ||
Prostą <math>y=kx+l</math> możemy opisać przy pomocy Delty Diraca, zakładając że punkty leżące na prostej mają nieskończoną amplitudę. | Prostą <math>y=kx+l</math> możemy opisać przy pomocy Delty Diraca, zakładając że punkty leżące na prostej mają nieskończoną amplitudę. | ||
| − | <equation><math> | + | <equation id="27"><math> |
g(x,y) = \delta(y-kx-l) | g(x,y) = \delta(y-kx-l) | ||
</math></equation> | </math></equation> | ||
wtedy: | wtedy: | ||
| − | <equation><math> | + | <equation id="28"><math> |
g(x,y)=\left\{ | g(x,y)=\left\{ | ||
\begin{array}{ccc} | \begin{array}{ccc} | ||
| Linia 255: | Linia 255: | ||
</math></equation> | </math></equation> | ||
jej transformata Radona jest równa: | jej transformata Radona jest równa: | ||
| − | <equation><math> | + | <equation id="29"><math> |
G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy | G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy | ||
</math></equation> | </math></equation> | ||
całkując prawą stronę powyższego równania najpierw po zmiennej dy oraz wykorzystując własność Delty Diraca dostajemy: | całkując prawą stronę powyższego równania najpierw po zmiennej dy oraz wykorzystując własność Delty Diraca dostajemy: | ||
| − | <equation><math> | + | <equation id="30"><math> |
G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy = \int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx | G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy = \int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx | ||
</math></equation> | </math></equation> | ||
W zależności od wartości parametrów <math>a,b,k,l</math> możemy rozważyć następujące przypadki rozwiązań: | W zależności od wartości parametrów <math>a,b,k,l</math> możemy rozważyć następujące przypadki rozwiązań: | ||
a. <math>k\neq a</math> oraz dowolne <math>l</math> i <math>b</math> | a. <math>k\neq a</math> oraz dowolne <math>l</math> i <math>b</math> | ||
| − | <equation><math> | + | <equation id="31"><math> |
G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy = \int_{-\infty}^{\infty}\delta(x+\frac{b-l}{a-k})dx | G(a,b)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(y-ax-b)\delta(y-kx-l)dxdy = \int_{-\infty}^{\infty}\delta(x+\frac{b-l}{a-k})dx | ||
</math></equation> | </math></equation> | ||
Korzystając z własności B Delty Diraca ostatecznie otrzymujemy: | Korzystając z własności B Delty Diraca ostatecznie otrzymujemy: | ||
| − | <equation><math> | + | <equation id="32"><math> |
G(a,b)=\frac{1}{|a-k|}\int_{-\infty}^{\infty}\delta(x+\frac{b-l}{a-k})dx=\frac{1}{|a-k|} | G(a,b)=\frac{1}{|a-k|}\int_{-\infty}^{\infty}\delta(x+\frac{b-l}{a-k})dx=\frac{1}{|a-k|} | ||
</math></equation> | </math></equation> | ||
b. <math>k=a</math> i <math>l\neq b</math>, wtedy: | b. <math>k=a</math> i <math>l\neq b</math>, wtedy: | ||
| − | <equation><math> | + | <equation id="33"><math> |
G(a,b)=\int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx=0 | G(a,b)=\int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx=0 | ||
</math></equation> | </math></equation> | ||
c. <math>k=a</math> i <math>l=b</math> | c. <math>k=a</math> i <math>l=b</math> | ||
| − | <equation><math> | + | <equation id="34"><math> |
G(a,b)=\int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx=\int_{-\infty}^{\infty}\delta(0)dx=\infty | G(a,b)=\int_{-\infty}^{\infty}\delta((a-k)x+b-l)dx=\int_{-\infty}^{\infty}\delta(0)dx=\infty | ||
</math></equation> | </math></equation> | ||
| Linia 293: | Linia 293: | ||
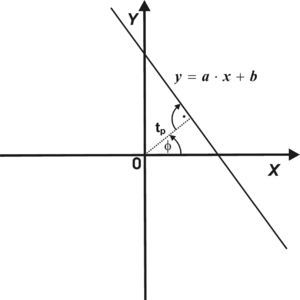
Na początku dokonajmy parametryzacji prostej — zamiast opisywać prostą za pomocą współczynnika ''a'' (nachylenia prostej względem układu OX) oraz współczynnika ''b'' — przecięcia prostej z osią OY wprowadzimy parametry <math>t_p</math>, określający odległość prostej od początku układu współrzędnych oraz kąt φ jaki tworzy normalna do prostej względem osi ''OX''. Znaczenie parametrów <math>t_p</math> i φ zilustrowano na <xr id="fig:punkt_prosta_0">rys. %i</xr>. Przy pomocy parametrów <math>t_p</math> i φ równanie prostej może być zapisane w następujący sposób: | Na początku dokonajmy parametryzacji prostej — zamiast opisywać prostą za pomocą współczynnika ''a'' (nachylenia prostej względem układu OX) oraz współczynnika ''b'' — przecięcia prostej z osią OY wprowadzimy parametry <math>t_p</math>, określający odległość prostej od początku układu współrzędnych oraz kąt φ jaki tworzy normalna do prostej względem osi ''OX''. Znaczenie parametrów <math>t_p</math> i φ zilustrowano na <xr id="fig:punkt_prosta_0">rys. %i</xr>. Przy pomocy parametrów <math>t_p</math> i φ równanie prostej może być zapisane w następujący sposób: | ||
| − | <equation><math> | + | <equation id="35"><math> |
\begin{array}{l} | \begin{array}{l} | ||
y = ax + b \\ | y = ax + b \\ | ||
| Linia 314: | Linia 314: | ||
Przypomnijmy znaną z kursu matematyki transformację współrzędnych punktu <math>x_0,y_0</math> w układzie ''X-Y'' do układu ''T-S'', obróconego względem niego o kąt <math>\phi</math>. W układzie ''T-S'' punkt ma współrzędne <math>t_0,s_0</math>: | Przypomnijmy znaną z kursu matematyki transformację współrzędnych punktu <math>x_0,y_0</math> w układzie ''X-Y'' do układu ''T-S'', obróconego względem niego o kąt <math>\phi</math>. W układzie ''T-S'' punkt ma współrzędne <math>t_0,s_0</math>: | ||
| − | <equation><math> | + | <equation id="36"><math> |
\begin{array}{lcl} | \begin{array}{lcl} | ||
t_0 & = & x_0\cos(p)+y_0\sin(p) \\ | t_0 & = & x_0\cos(p)+y_0\sin(p) \\ | ||
| Linia 322: | Linia 322: | ||
</math></equation> | </math></equation> | ||
<br> | <br> | ||
| − | <equation><math> | + | <equation id="37"><math> |
\begin{array}{lcl} | \begin{array}{lcl} | ||
x_0 &=& t_0\cos(p)+s_0\sin(p) \\ | x_0 &=& t_0\cos(p)+s_0\sin(p) \\ | ||
| Linia 331: | Linia 331: | ||
Zagadnienie to zilustrowano na <xr id="fig:obrót_układu_współrzędnych">rys. %i</xr>. | Zagadnienie to zilustrowano na <xr id="fig:obrót_układu_współrzędnych">rys. %i</xr>. | ||
Jakobian tego przekształcenia wynosi: | Jakobian tego przekształcenia wynosi: | ||
| − | <equation><math> | + | <equation id="38"><math> |
\det\left\{ | \det\left\{ | ||
\begin{array}{cc} | \begin{array}{cc} | ||
| Linia 351: | Linia 351: | ||
Parametryzacja prostej za pomocą przesunięcia <math>t_p</math> oraz kąta φ umożliwia następujący zapis Transformaty Radona: | Parametryzacja prostej za pomocą przesunięcia <math>t_p</math> oraz kąta φ umożliwia następujący zapis Transformaty Radona: | ||
| − | <equation><math> | + | <equation id="39"><math> |
G(t_p,\phi) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x,y)\delta(\sin(\phi) y+\cos(\phi)x-t_p)dxdy | G(t_p,\phi) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x,y)\delta(\sin(\phi) y+\cos(\phi)x-t_p)dxdy | ||
</math></equation> | </math></equation> | ||
| Linia 359: | Linia 359: | ||
* wykorzystaniu pewnych właściwości Delty Dirac'a. | * wykorzystaniu pewnych właściwości Delty Dirac'a. | ||
| − | <equation> | + | <equation id="40"> |
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
| Linia 393: | Linia 393: | ||
Rozważmy ponownie ważne zagadnienie, jakim jest Transformata Radona Punktu. Tak jak w przykładzie II punkt o współrzędnych <math>x_0,y_0</math> opiszemy za pomocą Delty Dirac'a. | Rozważmy ponownie ważne zagadnienie, jakim jest Transformata Radona Punktu. Tak jak w przykładzie II punkt o współrzędnych <math>x_0,y_0</math> opiszemy za pomocą Delty Dirac'a. | ||
| − | <equation><math> | + | <equation id="41"><math> |
\begin{array}{lcl} | \begin{array}{lcl} | ||
g(x,y) & = & \delta(x-x_0)\delta(y-y_0) \\ \\ | g(x,y) & = & \delta(x-x_0)\delta(y-y_0) \\ \\ | ||
| Linia 423: | Linia 423: | ||
[[File:punkt_prosta_biegunowe.png|300px|thumb|right|<figure id="fig:punkt_prosta_biegunowe"></figure>Wynikiem przekształcenia punktu opisanego w biegunowym układzie współrzędnych za pomocą Transformaty Radona jest krzywa sinusoidalna.]] | [[File:punkt_prosta_biegunowe.png|300px|thumb|right|<figure id="fig:punkt_prosta_biegunowe"></figure>Wynikiem przekształcenia punktu opisanego w biegunowym układzie współrzędnych za pomocą Transformaty Radona jest krzywa sinusoidalna.]] | ||
| − | <equation><math> | + | <equation id="42"><math> |
\begin{array}{l} | \begin{array}{l} | ||
x_0 = t_0\cos(\phi) \\ | x_0 = t_0\cos(\phi) \\ | ||
| Linia 440: | Linia 440: | ||
Otrzymaliśmy zatem następujący wynik: | Otrzymaliśmy zatem następujący wynik: | ||
| − | <equation><math> | + | <equation id="43"><math> |
\begin{array}{lcl} | \begin{array}{lcl} | ||
G(t_0,\phi) & = & \frac{1}{|\cos(\phi)|}\delta(\cos(\phi) x_0 - t_p + \sin(\phi) y_0) \\ \\ | G(t_0,\phi) & = & \frac{1}{|\cos(\phi)|}\delta(\cos(\phi) x_0 - t_p + \sin(\phi) y_0) \\ \\ | ||
| Linia 448: | Linia 448: | ||
Wyrażenie <math>\delta(t_0\sin(\phi + \phi_0) - t_p)</math> jest niezerowe, tylko wtedy, gdy: | Wyrażenie <math>\delta(t_0\sin(\phi + \phi_0) - t_p)</math> jest niezerowe, tylko wtedy, gdy: | ||
| − | <equation><math> | + | <equation id="44"><math> |
\begin{array}{l} | \begin{array}{l} | ||
t_0\sin(\phi + \phi_0) - t_p = 0 \\ | t_0\sin(\phi + \phi_0) - t_p = 0 \\ | ||
| Linia 463: | Linia 463: | ||
===Odwrotna Transformata Radona.=== | ===Odwrotna Transformata Radona.=== | ||
Poprzednie rozdziały dotyczyły tylko i wyłącznie Transformaty Radona oraz niektórych jej właściwości. Jaki związek ma Transformata Radona z rekonstrukcją obrazu badanego obiektu? Przypominamy, iż Transformata Radona jest pewnym rodzajem jedno-wymiarowego rzutowania. Obiekt badamy wzdłuż pewnej prostej, sparametryzowanej np. w biegunowym układzie współrzędnych. Wynikiem pojedynczego pomiary wzdłuż określonego przez prostą kierunku,jest suma punktów tworzących obiekt i leżących na tej prostej. Punkty te reprezentują pewną wybraną cechę obiektu. Okazuje się, że istnieje transformata odwrotna do Transformaty Radona, która na podstawie serii opisanych pomiarów umożliwia odtworzenie obrazu obiektu. Jeśli transformata obiektu <math>g(x,y)</math> ma postać: | Poprzednie rozdziały dotyczyły tylko i wyłącznie Transformaty Radona oraz niektórych jej właściwości. Jaki związek ma Transformata Radona z rekonstrukcją obrazu badanego obiektu? Przypominamy, iż Transformata Radona jest pewnym rodzajem jedno-wymiarowego rzutowania. Obiekt badamy wzdłuż pewnej prostej, sparametryzowanej np. w biegunowym układzie współrzędnych. Wynikiem pojedynczego pomiary wzdłuż określonego przez prostą kierunku,jest suma punktów tworzących obiekt i leżących na tej prostej. Punkty te reprezentują pewną wybraną cechę obiektu. Okazuje się, że istnieje transformata odwrotna do Transformaty Radona, która na podstawie serii opisanych pomiarów umożliwia odtworzenie obrazu obiektu. Jeśli transformata obiektu <math>g(x,y)</math> ma postać: | ||
| − | <equation><math> | + | <equation id="45"><math> |
G(t_p,\phi)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x,y)\delta(\sin(\phi) y+cos(\phi) x - t_p)dtd\phi | G(t_p,\phi)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x,y)\delta(\sin(\phi) y+cos(\phi) x - t_p)dtd\phi | ||
</math></equation> | </math></equation> | ||
to jej transformata odwrotna wynosi | to jej transformata odwrotna wynosi | ||
| − | <equation><math> | + | <equation id="46"><math> |
g(x,y)=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\frac{\frac{\delta G(t_p,\phi)}{\delta t_p}}{\sin(\phi) y+cos p x - t_p}dt_pd\phi | g(x,y)=\frac{1}{2\pi^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\frac{\frac{\delta G(t_p,\phi)}{\delta t_p}}{\sin(\phi) y+cos p x - t_p}dt_pd\phi | ||
</math></equation> | </math></equation> | ||
Aktualna wersja na dzień 20:52, 31 paź 2015
Spis treści
Wstęp

Poszczególne tkanki i narządy organizmu ludzkiego w różny sposób osłabiają promieniowanie X. Fakt ten został zaobserwowany jeszcze przez Wilhelma Roentgena, zaraz po odkryciu tego promieniowania i zastosowany do wykonywania zdjęć ręki. Trzy miesiące po odkryciu promieniowanie Rentgenowskiego wykorzystano je do prześwietlenia rannej głowy pacjenta. Po pierwszym roku stosowania promieniowania Rentgenowskiego w diagnostyce medycznej wiadomo było, że obraz wnętrze ciała ludzkiego powstaje na zasadzie rzucania przez poszczególne narządy, naświetlane promieniowaniem X, cieni na kliszę fotograficzną. Niestety, narządy organizmu ludzkiego wzajemnie się przesłaniają, co prowadzi od nakładania się na siebie obrazów poszczególnych struktur wewnętrznych człowieka. Ponadto, tworzenie zdjęć w klasycznej radiografii polega na rzutowaniu trójwymiarowego obiektu jakim jest człowiek na płaszczyznę, co dodatkowo zniekształca obraz. Wspominanie czynniki bardzo niekorzystnie wpłynęły na jakość zdjęć radiologicznych. Już w roku 1895 (rok po odkryciu promieniowania X), Elihu Thompson zauważył, iż wykonanie dwóch zdjęć radiologicznych z różnych pozycji lampy i detektora względem badanego obiektu, a następnie obejrzenie zdjęć w stroboskopie prowadzi do poprawienia jakości obrazu. Od tego momentu było wiadomo, iż wprowadzenie ruchu lampy Rentgenowskiej i detektora względem badanego obiektu pozwala otrzymać informację, umożliwiającą poprawę jakość zdjęć ciała ludzkiego. Zagadnienie to zilustrowano na rys. 1. Od tego momentu rozpoczęły się prowadzone na szeroką skalę badania nad problemem ruchu lampy rentgenowskiej i detektora względem pacjenta. Ich efektem było ciekawych rozwiązań, funkcjonujących jeszcze po zakończeniu drugiej wojny światowej. W międzyczasie, w roku 1917 austriacki matematyk Johann Radon, udowodnił pewne twierdzenie, które dzisiaj leży u podstaw tzw. metod rekonstrukcji obrazów. Praktyczna realizacja osiągnięcia Radona jest w zasadzie możliwa tylko przy pomocy komputerów, dlatego na początku dwudziestego wieku twierdzenie to przeszło niezauważone. Twierdzenie tym zajmiemy się na początku kolejnego rozdziału. W latach 50-tych i 60-tych ubiegłego wieku, problem wykonywania przestrzennego obrazu ciała ludzkiego nadal nie był rozwiązany. Funkcjonowało wiele technik wykonywania tego rodzaju zdjęć, jednakże jakość uzyskiwanych obrazów nie była zadowalająca. Każdy z odkrywców nadawał opracowanej przez siebie metodzie własną nazwę, i tak do roku 1962 roku można było spotkać się z takimi terminami jak stratigraphy, planigraphy, body-section radiography, tomography, verigraphy, radiothomy. Wszystkie one dotyczyły rozwiązań, w których lampa rentgenowska i detektory wykonywały ruch dookoła pacjenta. Ostatecznie, w roku 1962 International Commision on Radioation Units and Measurements, zarekomendowała dla tych metod termin ‘’’Tomografia’’’ (gr. thomos – warstwa, graphein – rysować), czyli obrazowanie warstwowe. Od roku 1956 Allan McLeod Cormack, amerykański fizyk pochodzenia południowoafrykańskiego w ramach hobby interesuje się promieniowaniem X i dokonuje wyliczeń będących podwalinami współczesnej tomografii rentgenowskiej. Wyniki publikuje w Journal of Applied Physics w 1963 i 1964 roku. Prace te jednak nie zostają zauważone. W tych samych latach Godfrey Newbold Hounsfield, brytyjski inżynier elektronik pracuje nad urządzeniami tomograficznymi, jednakże bez znaczącego sukcesu. W końcu napotyka na obliczenia Cormack’a i w oparciu o nie buduje pierwszy Rentgenowski Tomograf Komputerowy (X – Ray Computed Tomography, CT, w żargonie lekarskim zwany po prostu tomografem), zaprezentowany w roku 1971 i nazwany EMI. CT znajduje się w użytku od roku 1972 (pierwszy zbadany pacjent). W roku 1979 Hounsfield i Cormack otrzymują nagrodę Nobla, z dziedziny fizjologii i medycyny za opracowanie Komputerowej Tomografii Rentgenowskiej (Hounsfield ponadto otrzymuje od Królowej Brytyjskiej tytuł szlachecki Sir).
Twierdzenie Radona i Transformata Radona
W roku 1905 W. Radon udowodnił następujące twierdzenie: „Obraz obiektu dwuwymiarowego można zrekonstruować na podstawie nieskończone ilości rzutów jednowymiarowych”. Jak okaże się w dalszych częściach poniższego rozdziału, rzutowanie to odpowiada wykonywaniu na obiekcie pewnej transformacji, nazywanej Transformacją Radona. Dokonanie na wynikach rzutowania Odwrotnej Transformacji Radona umożliwia zrekonstruowanie obrazu obiektu. W następnym podrozdziale podamy matematyczne sformułowanie tego twierdzenia, natomiast w tym miejscu pragniemy zwrócić uwagę na pewien fakt. W twierdzeniu pojawia się termin rekonstrukcja. Otóż, w przeciwieństwie do klasycznej radiografii, w której zdjęcie obiektu powstaje natychmiast na filmie, potem zaś obraz jest tylko wywoływany i utrwalany, w przypadku tomografii, nie można na podstawie serii pomiarów od razu uzyskać obrazu. Niezbędny jest dodatkowy etap – wyznaczenie na podstawie zebranych danych obrazu badanego obiektu. Proces ten nazywamy rekonstrukcją.
Podstawy Matematyczne — Delta Diraca
Poprawne zrozumienie Twierdzenia Radona wymaga opanowania pewnych zagadnień matematycznych, które przypomnimy w poniższym podrozdziale.
właściwości:
A.
B.
C.
D.
E.
F.
Inne ciekawe właściwości wynikające z właściwości A-F:
G.
Dowód:
H.
Dowód:
[math]
\delta(ax+b)=\delta(a(x+\frac{b}{a}))={1}{|a|}\delta(x+\frac{b}{a})
[/math]
I.
Dowód:
[math] \begin{array}{l} \int_{-\infty}^{\infty} g(x)\delta(ax+b)dx=\int_{-\infty}^{\infty} g(x)\delta(a(x+\frac{b}{a}))dx \\ \\ \int_{-\infty}^{\infty} g(x)\delta(a(x+\frac{b}{a}))dx=\frac{1}{|a|}\int_{-\infty}^{\infty} g(x)\delta(x+\frac{b}{a}))dx \\ \\ x+\frac{b}{a}=x'\\ \\ x=x'-\frac{b}{a} \\ \\ dx = dx' \\ \\ \int_{-\infty}^{\infty} g(x)\delta(x+\frac{b}{a})dx = \int_{-\infty}^{\infty} g(x'-\frac{b}{a})\delta(x')dx' \\ \\ \int_{-\infty}^{\infty} g(x'-\frac{b}{a})\delta(x')dx' =\frac{1}{|a|}g(-\frac{b}{a}) \\ \end{array} [/math]
Transformata Radona w kartezjańskim układzie współrzędnych
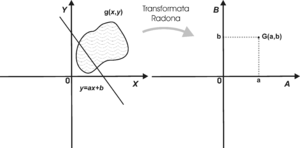
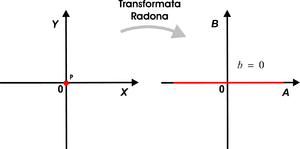
Transformata Radona to transformata całkowa o następującej postaci:
Transformatę Radona zilustrowano na rys. 2.
Własności:
A. Transformata Radona jest liniowa.
Dowód:
Niech będzie dana funkcja [math]h(x,y)[/math], będąca kombinacją liniową funkcji [math]g_i(x,y)[/math]:
Wtedy jej transformata Radona [math]h(x,y)[/math] wynosi:
i jest kombinacją liniową transformat Radona funkcji [math]g_i(x,y)[/math].
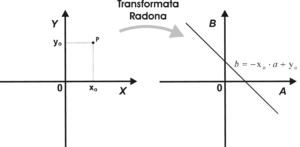
B. Transformata Radona funkcji przesuniętej do współrzędnych [math](x_0,y_0)[/math]
Dokonując zamiany zmiennych:
dostajemy:
suma wyrażeń: [math]kx_0+b-y_0[/math] jest pewną stałą, będącą nowym współczynnikiem przesunięcia prostej względem początku układu współrzędnych, wzdłuż której następuje całkowanie funkcji Ostatecznie dostajemy następujący wynik. Jeżeli transformata Radona funkcji [math]g(x,y)[/math] wynosi [math]G(a,b)[/math], to transformata Radona funkcji [math]g(x-x_0,y-y_0)[/math] jest równa:
Przykład 1. Transformata Radona punktu znajdującego się w środku układu współrzędnych.
Zakładamy, że punkt ma nieskończenie wielką amplitudę. Taki punkt możemy zamodelować za pomocą Delty Diraca:
co oznacza, że funkcja [math]g(x,y)[/math] ma następującą postać:
Obliczmy transformatę Radona powyższej funkcji:
Przekształcimy ten wzór, korzystając z właściwości Delty Diraca.
Ostatecznie otrzymaliśmy zatem następujący wynik:
Jak widzimy, transformata Radona punktu, znajdującego się w środku układu współrzędnych da wynik niezerowy, jeśli współczynnik przesunięcia prostej będzie równy zero. Jest to wynik zgodny z naszą intuicją, bowiem, tylko prosta o takim współczynniku przesunięcia przechodzi przez środek układu współrzędnych, a zatem pokrywa się z rozważanym punktem. Innymi słowy, transformata Radona przekształca punkt leżący w początku układu współrzędnych, na prostą w przestrzeni parametrów Radona biegnącą równolegle do osi pionowej i przechodzącej przez punkt 0. Wynik ten zilustrowano na rys. 3.
Przykład 2. Transfromata Radona punktu o dowolnych współrzędnych [math](x_0,y_0)[/math]
Jest to bardzo ważny przykład, ponieważ każdy obiekt możemy przedstawić jako sumę punktów o różnych współrzędnych, których amplituda reprezentuje pewną cechę fizyczną obiektu. Wykorzystując dalej liniowość Transformaty Radona, możemy obliczyć Transformatę Radona danego obiektu jako sumę Transformat Radona punktów składających się na ten obiekt. Podobnie jak w poprzednim przykładzie, punkt możemy wyrazić za pomocą Delty Diraca.
Postać funkcji [math]g(x,y)[/math] jest zatem następująca:
Transformatę Radona powyższej funkcji obliczymy wykorzystując właściwości B transformaty Radona. Transformatę Radona punktu leżącego w środku układu współrzędnych wynosi: [math] g(x,y) = \delta(x)(y)\xrightarrow{\textrm{Transfromata Radona}}G(a,b)=\delta(b) [/math] a zatem transformata Radona punktu przesuniętego jest równa:
Transformata Radona przekształca zatem punkt o dowolnych współrzędnych w prostą w przestrzeni parametrów Radona. Wynik ten zilustrowano na rys. 4
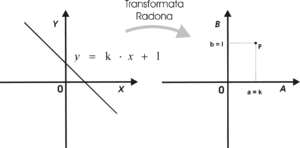
Przykład 3. Transformata Radona prostej.
Przykład ten podajemy ze względu na jego znaczenie w grafice komputerowej. Uprzedzając wyniki obliczeń podamy, iż Transformata Radona punktu w kartezjańskim układzie współrzędnych prowadzi do punktu we układzie współrzędnych Transformaty Radona. Punkt te ma współrzędne odpowiadające parametrom prostej. W ten sposób można wykorzystać Transformatę Radona do wynajdywanie w obiekcie, czy obrazach linii prostych.
Prostą [math]y=kx+l[/math] możemy opisać przy pomocy Delty Diraca, zakładając że punkty leżące na prostej mają nieskończoną amplitudę.
wtedy:
jej transformata Radona jest równa:
całkując prawą stronę powyższego równania najpierw po zmiennej dy oraz wykorzystując własność Delty Diraca dostajemy:
W zależności od wartości parametrów [math]a,b,k,l[/math] możemy rozważyć następujące przypadki rozwiązań: a. [math]k\neq a[/math] oraz dowolne [math]l[/math] i [math]b[/math]
Korzystając z własności B Delty Diraca ostatecznie otrzymujemy:
b. [math]k=a[/math] i [math]l\neq b[/math], wtedy:
c. [math]k=a[/math] i [math]l=b[/math]
Podsumowując, transformata Radona funkcji prostej przekształca ją w przestrzeni (A-B) w funkcję płaską o amplitudzie [math]\frac{1}{|a-k|}[/math], która osiąga wartość nieskończoną w punkcie o współrzędnych odpowiadających parametrom prostej. Wynik ten zilustrowano na rys. 5
Normalna postać Transformaty Radona
Obiekty spotykane w rzeczywistości cechuje zwykle pewna symetria, w związku z czym dogodniej jest je opisywać w innych niż kartezjańskim układzie współrzędnych. Np. człowiek w przybliżeniu posiada symetrię walcową. Ponadto Twierdzenie Radona mówi o tym, iż do wiernego zrekonstruowania obiektu potrzebna jest nieskończona liczba rzutów tego obiektu. Warunek ten w praktyce jest oczywiście niemożliwy do zrealizowania, w związku z czym zawsze będziemy mieli do czynienia z obrazem będącym pewnym przybliżeniem rzeczywistego obiektu. Niemniej powstaje pytanie, z jakich kierunków dokonać rzutowania badanego obiektu. Okazuje się, że dowolne ruchy występujące w przyrodzie, można uzyskać za pomocą obrotu i przesunięcia. Uwzględniając symetrię ciała człowieka, wspomniane ruchy wygodniej jest opisywać w biegunowym układzie współrzędnych. Przejdziemy teraz zatem do wyrażenia Transformaty Radona w biegunowym układzie współrzędnych, którą będziemy nazywać Normalną Transformatą Radona. Pomocne przy tym będą dwa dodatkowe zagadnienia — parametryzacja proste jw układzie biegunowym oraz obrót układu współrzędnych, które opiszemy w następnych rozdziałach.
Parametryzacja prostej w układzie biegunowym .
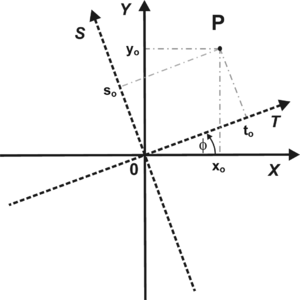
Na początku dokonajmy parametryzacji prostej — zamiast opisywać prostą za pomocą współczynnika a (nachylenia prostej względem układu OX) oraz współczynnika b — przecięcia prostej z osią OY wprowadzimy parametry [math]t_p[/math], określający odległość prostej od początku układu współrzędnych oraz kąt φ jaki tworzy normalna do prostej względem osi OX. Znaczenie parametrów [math]t_p[/math] i φ zilustrowano na rys. 3. Przy pomocy parametrów [math]t_p[/math] i φ równanie prostej może być zapisane w następujący sposób:
Obrót układu współrzędnych:
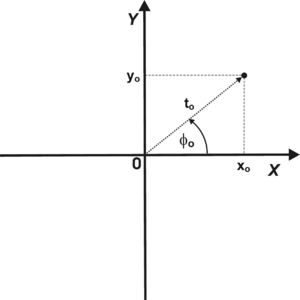
Przypomnijmy znaną z kursu matematyki transformację współrzędnych punktu [math]x_0,y_0[/math] w układzie X-Y do układu T-S, obróconego względem niego o kąt [math]\phi[/math]. W układzie T-S punkt ma współrzędne [math]t_0,s_0[/math]:
Zagadnienie to zilustrowano na rys. 7. Jakobian tego przekształcenia wynosi:
Normalna Transformata Radona
Parametryzacja prostej za pomocą przesunięcia [math]t_p[/math] oraz kąta φ umożliwia następujący zapis Transformaty Radona:
Dokonamy teraz pewnych przekształceń, polegających na:
- wykorzystaniu transformacji układu współrzędnych pomiędzy układem X-Y i układem obróconym T-S,
- wykorzystaniu pewnych właściwości Delty Dirac'a.
[math]
\begin{array}{l}
t - t_p=t' \\ \\
t = t'+t_p \\ \\
dt = dt' \\ \\
\end{array}
[/math]
Otrzymany wzór to alternatywna postać Normalnej Transformaty Radona. Prosze zauważyć, iż wyrażenie
Przykład IV — Normalna transformata Radona punktu
Rozważmy ponownie ważne zagadnienie, jakim jest Transformata Radona Punktu. Tak jak w przykładzie II punkt o współrzędnych [math]x_0,y_0[/math] opiszemy za pomocą Delty Dirac'a.
Jak wygląda wykres otrzymanej funkcji [math]G(t_0,\phi)[/math]. Wygodniej będzie zapisać współrzędne punktu [math]x_0, y_0[/math] we współrzędnych biegunowych, co zilustrowano na rys. 8.
Otrzymaliśmy zatem następujący wynik:
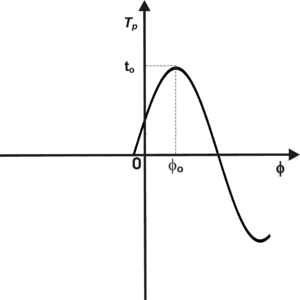
Wyrażenie [math]\delta(t_0\sin(\phi + \phi_0) - t_p)[/math] jest niezerowe, tylko wtedy, gdy:
czyli gdy punkty [math]t_p[/math] i [math]\phi[/math] leżą na sinusoidzie. Wynik ten zilustrowano na zilustrowano na rys. 9.
Sinogram
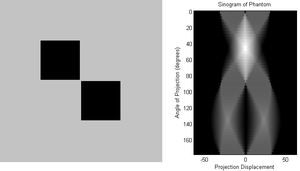
Jak już to było wspomniane w poprzednich rozdziałach, dowolny obiekt możemy zapisać jako sumę punktów o różnych współrzędnych. W związku z tym, iż Transformatą Radona punktu w biegunowym układzie współrzędnych jest krzywa sinusoidalna, Transformata Radona dowolnego obiektu będzie składała się z bardzo wielu sinusoid. Jest to powód, dla którego wykres Transformaty Radona nazywamy sinogramem. Przykład obiektu i jego sinogramu zaprezentowano na rys. 10.
Odwrotna Transformata Radona.
Poprzednie rozdziały dotyczyły tylko i wyłącznie Transformaty Radona oraz niektórych jej właściwości. Jaki związek ma Transformata Radona z rekonstrukcją obrazu badanego obiektu? Przypominamy, iż Transformata Radona jest pewnym rodzajem jedno-wymiarowego rzutowania. Obiekt badamy wzdłuż pewnej prostej, sparametryzowanej np. w biegunowym układzie współrzędnych. Wynikiem pojedynczego pomiary wzdłuż określonego przez prostą kierunku,jest suma punktów tworzących obiekt i leżących na tej prostej. Punkty te reprezentują pewną wybraną cechę obiektu. Okazuje się, że istnieje transformata odwrotna do Transformaty Radona, która na podstawie serii opisanych pomiarów umożliwia odtworzenie obrazu obiektu. Jeśli transformata obiektu [math]g(x,y)[/math] ma postać:
to jej transformata odwrotna wynosi
Podana postać odwrotnej Transformaty Radona jest niewygodna do implementacji numerycznej (wymaga czasochłonnego liczenia wielu pochodnych), niemniej jest dowodem na to, iż możliwa jest na podstawie jednowymiarowych rzutów rekonstrukcja obrazu dwu lub trój wymiarowego obiektu. Pozostaje jeszcze kwestia, jak aparatura medyczna jest w stanie dokonać wyznaczenia Transformaty Radona obiektu. Tematem tym zajmiemy się w kolejnych rozdziałach.