PPy3/Matplotlib: Różnice pomiędzy wersjami
| (Nie pokazano 10 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 187: | Linia 187: | ||
import numpy as np | import numpy as np | ||
import matplotlib.pyplot as plt | import matplotlib.pyplot as plt | ||
| − | import | + | from scipy.stats import norm |
mi, sigma = 100, 15 | mi, sigma = 100, 15 | ||
| Linia 197: | Linia 197: | ||
| − | n, bins, patches = plt.hist(x, 50, | + | n, bins, patches = plt.hist(x, 50, density=True, |
| + | facecolor='green', edgecolor='black', alpha=0.75) | ||
# Tu w jawny sposób odbieramy zwracane przez plt.hist obiekty | # Tu w jawny sposób odbieramy zwracane przez plt.hist obiekty | ||
# Zmieniamy też: | # Zmieniamy też: | ||
| Linia 209: | Linia 210: | ||
# zwróconych przez plt.hist w macierzy bins | # zwróconych przez plt.hist w macierzy bins | ||
| − | y = | + | y = norm.pdf( bincenters, mi, sigma) |
# obliczamy wartości w normalnym rozkładzie gęstości prawdopodobieństwa | # obliczamy wartości w normalnym rozkładzie gęstości prawdopodobieństwa | ||
# o średniej mi i wariancji sigma**2 dla wartości bincenters | # o średniej mi i wariancji sigma**2 dla wartości bincenters | ||
| Linia 222: | Linia 223: | ||
[[Grafika:Hist2.gif]] | [[Grafika:Hist2.gif]] | ||
| + | ==Krzywa parametryczna== | ||
| + | |||
| + | Rysowanie krzywej danej w postaci parametrycznej niewiele się różni od rysowania wykresu funkcji. Żeby było zabawniej, wykonam jeszcze przy okazji rachunek Monte Carlo oraz jego wizualizację. | ||
| + | |||
| + | Krzywa, jaką tutaj narysujemy to tzw. [https://pl.wikipedia.org/wiki/Lemniskata_Gerona lemniskata Gerona]. Zostanie dodatkowo opisana okręgiem jednostkowym; następnie, wylosuję dużą liczbę punktów o równomiernym rozkładzie leżących w kwadracie opisanym na tym okręgu. Robię tak, ponieważ łatwo mi jest wylosować tablicę wielu liczb z zakresu (0, 1) — jest do tego gotowa funkcja <tt>numpy.random.random</tt>, następnie przeskalować i przesunąć je do odcinka (-1, 1). Wreszcie, traktując je jako pary współrzędnych <tt>(x, y)</tt>, pozostawiam tylko te, które znalazły się we wnętrzu koła jednostkowego (odrzucając pozostałe), i dzielę na te, które znalazły się w obszarze wewnątrz lemniskaty, i te, które znalazły się na zewnątrz. | ||
| + | |||
| + | Intuicyjnie jest dość jasne, że — o ile losowaliśmy punkty rzeczywiście w sposób równomierny — stosunek liczby „trafień" w obszar ograniczony lemniskatą do liczby wszystkich „trafień" w obszar koła będzie w przybliżeniu równy stosunkowi pól powierzchni tych obszarów. I na tym tu poprzestaniemy; to, jak dokładne to może być przybliżenie, czyli jakiej wielkości błędu możemy oczekiwać, to już problem na inne zajęcia... | ||
| + | |||
| + | <source lang=python> | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | Φ = np.arange(0, 2*np.pi, 2*np.pi/600) | ||
| + | X = np.cos(Φ) | ||
| + | Y = np.sin(2*Φ) / 2 # = np.sin(Φ) * np.cos(Φ) | ||
| + | plt.axes(aspect='equal') # to mi gwarantuje, że okrąg nie wyjdzie „spłaszczony" | ||
| + | plt.plot(X, Y, 'b') | ||
| + | YO = np.sin(Φ) | ||
| + | plt.plot(X, YO, 'k') | ||
| + | # biorę całą kupę losowych punktów z przedziału (-1, 1) | ||
| + | P = np.random.random((100000, 2)) * 2 - 1 # milion par (x, y) | ||
| + | # wyrzucam te, które są poza kołem x**2 + y**2 < 1 | ||
| + | P = P[(P**2).sum(axis=1) < 1] | ||
| + | # dzielę na te co wewnątrz lemniskaty, i te co na zewnątrz | ||
| + | I_in = np.abs(P[:,1]) < np.abs(P[:,0]) * np.sqrt(1 - P[:,0]**2) | ||
| + | P_in = P[I_in] | ||
| + | P_out = P[~I_in] | ||
| + | # maluję wewnętrzne na niebiesko | ||
| + | plt.plot(P_in[:,0], P_in[:,1], 'b,') | ||
| + | # a zewnętrzne na czerwono | ||
| + | plt.plot(P_out[:,0], P_out[:,1], 'r,') | ||
| + | # powierzchnia to z grubsza stosunek l. punktów wewnętrznych do wszystkich | ||
| + | S = P_in.size / P.size | ||
| + | plt.title('Pole pow. wnętrza lemniskaty to ok. {:.3f} pola pow. koła'.format(S)) | ||
| + | plt.show() | ||
| + | </source> | ||
| + | |||
| + | Przy okazji, jak widać w kodzie Pythona (wersja 3) można bezproblemowo używać liter z innych alfabetów, nie tylko łacińskiego. Niestety nie wszystkie systemy operacyjne zapewniają bezproblemową obsługę pełnego zestawu liter wszelkich języków, dlatego na ogół wykorzystywanie liter z egzotycznych systemów pisma nie jest szczególnie zalecane. | ||
| + | |||
| + | W wyniku uruchomienia tego programu powinno pojawić się okno z obrazkiem podobnym do poniższego: | ||
| + | |||
| + | [[File:Lemniskata.png]] | ||
==Wizualizacja zawartości tablicy dwuwymiarowej== | ==Wizualizacja zawartości tablicy dwuwymiarowej== | ||
| Linia 280: | Linia 323: | ||
[[Grafika:reading-girl-hist.png]] | [[Grafika:reading-girl-hist.png]] | ||
| + | |||
| + | Wykonaliśmy w ten sposób histogram opisujący rozkład natężenia pikseli obrazka. | ||
==Wiele wykresów w jednym oknie== | ==Wiele wykresów w jednym oknie== | ||
==Ćwiczenia== | ==Ćwiczenia== | ||
| + | |||
| + | 1. Spróbuj znaleźć sposób przekształcenia obrazka takiego, jak poniższy portret autora skryptu: | ||
| + | |||
| + | [[Grafika:rjb_small.jpg]] | ||
| + | |||
| + | do postaci przypominającej | ||
| + | |||
| + | [[Grafika:rjb_bw.png]] | ||
| + | |||
| + | 2. (''Nieco złożone'') Napisz program symulujący „bilard na kółku". Dokładniej: wewnątrz koła jednostkowego na płaszczyźnie porusza się cząstka (punkt), zachowując stałą prędkość — dopóki nie napotka brzegu, czyli okręgu; wówczas odbija się zgodnie z zasadą, że kąt padania równa się kątowi odbicia; chodzi o kąt pomiędzy wektorem prędkości a promieniem okręgu jednostkowego w miejscu, gdzie tor ruchu przecina się z okręgiem, po odbiciu jest on taki sam co do wartości ale ''po drugiej stronie'' promienia. Program rysuje okręg jednostkowy oraz tor ruchu cząstki wewnątrz tego okręgu, w zależności od początkowego położenia, kierunku początkowej prędkości (wartość prędkości jest nieistotna, ponieważ jest stała), i czasu obserwacji. | ||
| + | |||
| + | Wynikiem programu są wykresy podobne do poniższego: | ||
| + | |||
| + | [[Grafika:bilard_na_kole.png]] | ||
| + | |||
| + | czarną kropką oznaczono położenie początkowe, a na zielono — końcowe. | ||
| + | |||
---- | ---- | ||
| − | [[PPy3/NumPy|poprzednie]] | [["Programowanie z Pythonem3"|strona główna]] | [[PPy3/ | + | [[PPy3/NumPy|poprzednie]] | [["Programowanie z Pythonem3"|strona główna]] | [[PPy3/TematyDodatkowe]] |
--[[Użytkownik:RobertJB|RobertJB]] ([[Dyskusja użytkownika:RobertJB|dyskusja]]) 14:05, 10 kwi 2017 (CEST) | --[[Użytkownik:RobertJB|RobertJB]] ([[Dyskusja użytkownika:RobertJB|dyskusja]]) 14:05, 10 kwi 2017 (CEST) | ||
Aktualna wersja na dzień 09:45, 8 sty 2021
Spis treści
- 1 Matplotlib - wizualizacja danych
Matplotlib - wizualizacja danych
Wprowadzenie do pakietu Matplotlib na przykładach
Pakiet Matplotlib bazuje na pakiecie numerycznym Numpy i korzysta z obiektów w nim zawartych. Pokażemy, jak z jego pomocą rysować różnorodne wykresy prezentujące graficznie przetwarzane dane i wyniki obliczeń. Zamiast wyliczać zawartość pakietu pokażemy ich użyteczność na przykładach. Zaczniemy od prostych i będziemy po drodze omawiać zastosowane w nich konstrukcje.
Wykresy funkcji
y = f(x)
Prześledźmy działanie poniższego programu:
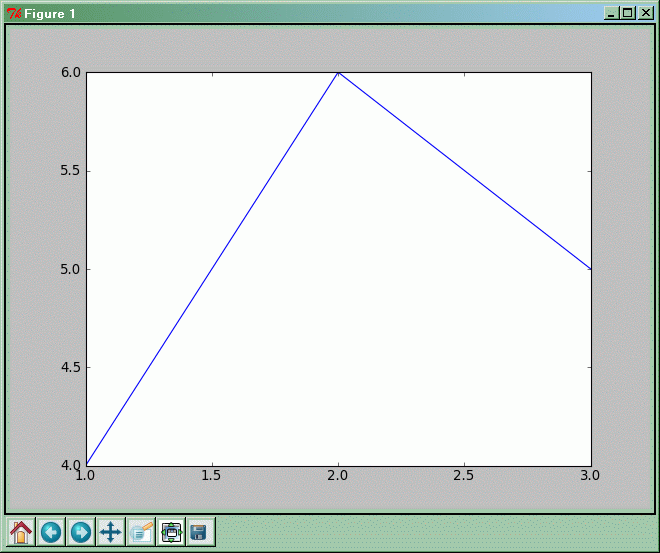
import matplotlib.pyplot as plt
x = [1,2,3]
y = [4,6,5]
plt.plot(x,y)
plt.show()
- Rezultat
- Jak to działa?
Aby skorzystać z pakietu graficznego Matplotlib importujemy go do naszego programu poleceniem import.
Pod-pakiet pyplot jest jednym z paru nieco różnych interfejsów do Matplotlib - tj. sposobów wykorzystania jego funkcjonalności. Inny, też często wykorzystywany, nazywa się pylab i można go importować wprost (import pylab). Pyplot zapewnie nieco większą elastyczność, chociaż dla najprostszych przykładów - takich, jakie tu omówimy - nie ma istotnej różnicy.
Wytwarzamy dwie listy x i y zawierające ciągi liczb 1, 2, 3 oraz 4, 6, 5.
Funkcja plot rysuje wykres i umieszcza na nim punkty o współrzędnych zawartych w listach przekazanych jej jako argumenty. Pierwszy argument zawiera współrzędne x-owe kolejnych punktów, a drugi argument współrzędne y-owe kolejnych punktów wykresu. Ponieważ listy mają po trzy elementy, tak więc wykres zawierać będzie trzy punkty o współrzędnych (1, 4), (2, 6) oraz (3, 5). Domyślnie punkty na wykresie łączone są ze sobą niebieską linią ciągłą. To oczywiście można zmienić - dodając opcjonalne parametry do wywołania plot można uzyskać linię o innym kolorze, linię przerywaną, z kropek, albo w ogóle brak linii - a za to np. duże kropki (trójkąty, gwiazdki, ...) w miejscach odpowiadających punktom danych.
Po wywołaniu funkcji plot wykres nie pokazuje się jeszcze na ekranie. Aby go pokazać, używamy funkcji show. Wykres pojawia się na ekranie w osobnym oknie, a Python czeka z wykonywaniem kolejnych instrukcji do momentu zamknięcia okna z wykresem.
W okienku wykresu mamy kilka guzików (po lewej stronie na dole). Służą one do manipulowania wyglądem rysunku. Guzikiem z krzyżykiem możemy zmniejszać/zwiększać skalę na osiach (wciskając prawy guzik myszy i przesuwając kursor po obrazku) oraz przesuwać cały wykres (wciskając lewy guzik myszy i przesuwając kursor po obrazku). Guzik z okienkiem i strzałkami pozwala także zmieniać rozmiar i położenie osi wykresu wewnątrz okna wybierając właściwe wartości. Guzik z domkiem przywraca wyjściowe ustawienia rysunku. Guzik z obrazkiem dyskietki (czy ktoś jeszcze wie, co to takiego?) pozwala zachować wykres (jego aktualny stan, czyli z uwzględnieniem dokonanych interaktywnie modyfikacji) jako plik graficzny jednego z kilku formatów.
Rysujemy wykres funkcji sinus
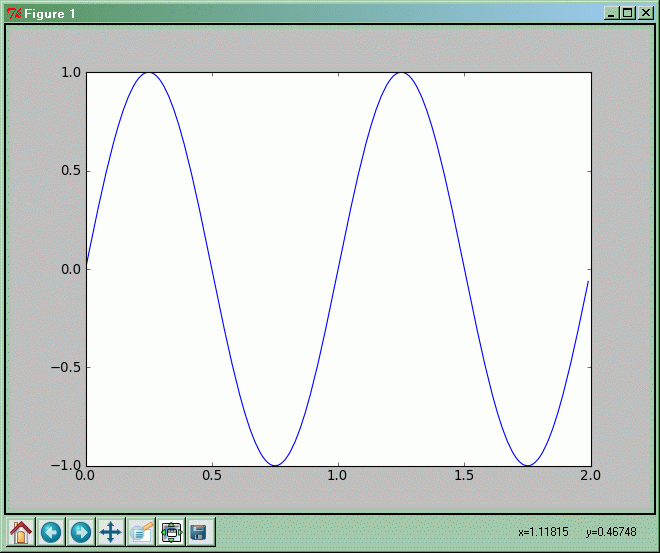
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y = np.sin(2.0*np.pi*x)
plt.plot(x,y)
plt.show()
- Rezultat
- Jak to działa?
Oprócz funkcji z Matplotlib będziemu tu odwoływać się również wprost do elementów z pakietu NumPy.
Funkcja arange jest podobna do standardowej funkcji range wytwarzającej określone sekwencje liczb w postaci listy. Funkcja arange zamiast listy wytwarza tablicę zawierającą ciąg liczb zmiennoprzecinkowych zaczynający się od pierwszego podanego argumentu funkcji arange (u nas 0.0), a kończący się przed drugim argumentem (tradycyjnie, ciąg wynikowy nie zawiera wartości podanej jako drugi argument, u nas 2.0). Różnica między elementami wytworzonego ciągu domyślnie wynosi 1, ale jeśli podamy funkcji arange trzeci argument, to definiuje on nową różnicę ciągu, u nas wynosi on 0.01.
Tak więc zmienna x jest tablicą-wektorem zawierającą ciąg liczb od 0 do 1,99 co 0,01 (czyli 0, 0,01, 0,02, ..., 1,98, 1,99).
Funkcja sin służy do obliczania wartości funkcji sinus dla argumentu podanego w radianach. A co u nas jest argumentem tej funkcji? Wyrażenie będące argumentem zawiera mnożenie liczby 2.0 przez pi (pochodzące z pakietu NumPy), a następnie mnożenie wyniku przez tablicę x. Zmienna pi zawiera przybliżoną wartość matematycznej stałej π ≈ 3,1415926... Mnożenie liczby i tablicy, jak wiemy z poprzedniego punktu, daje w wyniku tablicę. Oznacza to, że argumentem funkcji sin jest nie liczba, ale tablica! Taka możliwość jest przewidziana przez twórców pakietu Numpy; wynikiem wywołania funkcji jest wtedy również tablica. Jest ona tej samej długości co tablica będąca argumentem wywołania funkcji.
Tak więc zmienna y zawiera ciąg wartości funkcji sinus policzonych dla wartości zawartych w zmiennej x pomnożonych każda przez 2π (czyli sin(2π·0), sin(2π·0,01), sin(2π·0,02), ..., sin(2π·1,98), sin(2π·1,99)).
Funkcja plot(x,y) narysuje zestaw punktów o współrzędnych (0, sin(2π·0)), (0,01, sin(2π·0,01)), (0,02, sin(2π·0,02)), ..., (1,98, sin(2π·1,98)), (1,99, sin(2π·1,99)) połączonych niebieską linią.
Ulepszamy wykres
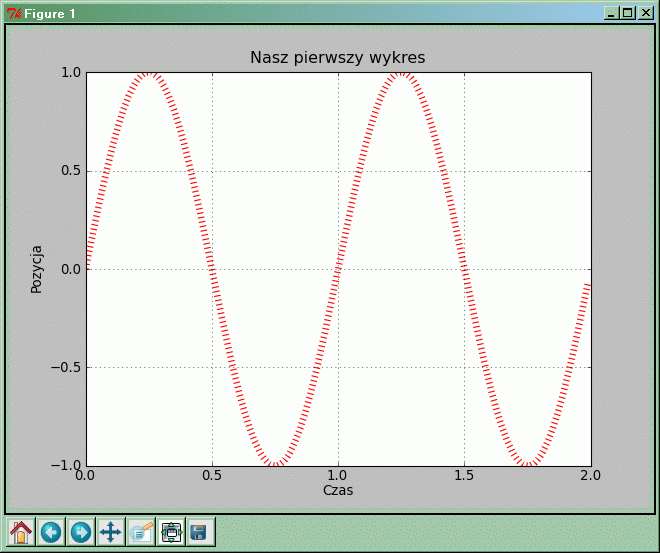
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y = np.sin(2.0*p.pi*x)
plt.plot(x,y,'r:',linewidth=6)
plt.xlabel('Czas')
plt.ylabel('Pozycja')
plt.title('Nasz pierwszy wykres')
plt.grid(True)
plt.show()
- Rezultat
- Jak to działa?
W porównaniu z poprzednim przykładem pojawiło się na wykresie kilka drobnych zmian i „ozdobników”.
W funkcji plot pojawiły się dwa nowe parametry:
- 'r:' — ten parametr steruje wyglądem rysowanej linii wykresu. Pierwsza litera tego napisu określa kolor linii (na przykład r: czerwony, b: niebieski, g: zielony, y: żółty, k: czarny). Drugi znak napisu określa wygląd samej linii (np. -: ciągła, :: kropkowana, o: okrągłe punkty bez linii, +: krzyżyki bez linii, itd.).
- linewidth=6 — ten parametr zmienia grubość rysowanej linii.
Dodaliśmy też wywołania funkcji xlabel i ylabel. Ich argumentami są napisy, które pojawią się jako opisy osi, odpowiednio poziomej i pionowej. Wywołanie funkcji title wypisuje przekazany jej napis jako tytuł całego wykresu.
Funkcja grid dorysowuje siatkę prostokątną na wykresie w wybranych punktach opisujących wartości na osiach wykresu. Punkty, w których wybierane są wartości opisane na osiach (ang. tick) są wybierane automatycznie (oczywiście jeśli chcemy, możemy zmieniać ich położenie i opisy odpowiednią funkcją, powiemy o tym później).
Kilka wykresów we wspólnych osiach - Pierwsza wersja
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y1 = np.sin(2.0*p.pi*x)
y2 = np.cos(2.0*p.pi*x)
plt.plot(x,y1,'r:',x,y2,'g')
plt.legend(('dane y1','dane y2'))
plt.xlabel('Czas')
plt.ylabel('Pozycja')
plt.title('Wykres ')
plt.grid(True)
plt.show()
- Jak to działa?
W jednym układzie współrzędnych możemy narysować wiele wykresów. Robimy to podając w jednym poleceniu plot kolejno zestawy parametrów opisujące poszczególne linie: współrzędne x, współrzędne y, sposób wykreślania linii. Aby łatwo identyfikować linie można dodać legendę poleceniem legend(). Sposób kontrolowania wyglądu i położenia legendy: help(plt.legend) (oczywiście po zaimportowaniu modułu: import matplotlib.pyplot as plt ).
Kilka wykresów we wspólnych osiach - Druga wersja
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y1 = np.sin(2.0*p.pi*x)
y2 = np.cos(2.0*p.pi*x)
y = y1*y2
l1, = plt.plot(x,y,'b')
l2,l3 = plt.plot(x,y1,'r:',x,y2,'g')
plt.legend((l2,l3,l1),('dane y1','dane y2','y1*y2'))
plt.xlabel('Czas')
plt.ylabel('Pozycja')
plt.title('Wykres ')
plt.grid(True)
plt.show()
- Jak to działa?
Wykresy możemy dodawać do współrzędnych kolejnymi poleceniami plot. Funkcja plot zwraca listę linii. Notacja l1, = plt.plot(x,y,'b') wydobywa z listy pierwszą linię (Gdyby po l1 nie było przecinka to l1 byłoby listą zawierającą jeden obiekt klasy linia ).
Dzięki nazwaniu poszczególnych obiektów linii możemy kontrolować ich kolejność (i obecność) na legendzie.
Histogram (diagram liczebności)
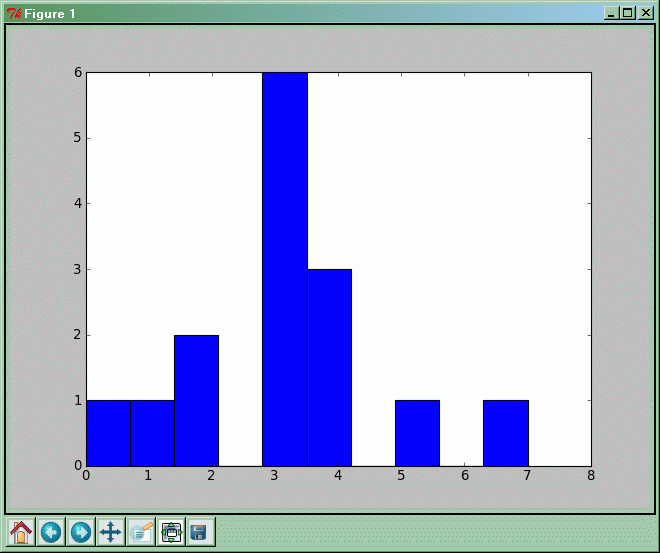
import matplotlib.pyplot as plt
zliczenia = [0, 1, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 7]
plt.hist(zliczenia)
plt.show()
- Jak to działa ?
Do zmiennej zliczenia przypisujemy sekwencję z ręcznie podanymi wartościami. Zakres zmienności badanych zliczeń (odkładany na osi X) zostanie podzielony na przedziały (ang. bin) o jednakowej „szerokości”; domyślnie będzie ich 10. Funkcja hist() zlicza wystąpienia wartości w binach i rysuje histogram. Funkcja ta zwraca krotkę (array ze zliczeniami, array z binami, lista zawierająca prostokąty, które histogram rysuje, tzw. obiekty Patch).
Porządek wartości, których histogram zostanie stworzony nie ma znaczenia. Mogą one oczywiście być umieszczone również w tablicy NumPy.
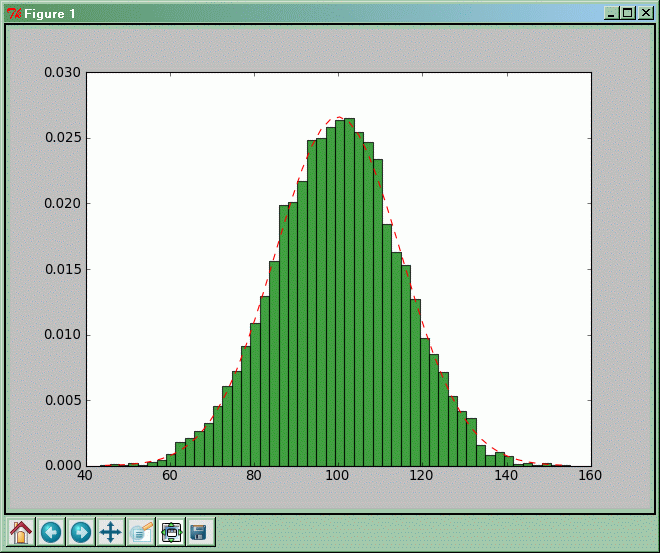
Przykład bardziej zaawansowany
Wyjaśnienie działania znajduje się w komentarzach do programu:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
mi, sigma = 100, 15
x = mi + sigma * np.random.randn(10000)
# numpy.random.randn zwraca array z liczbami pseudolosowymi
# pochodzącymi z rozkładu normalnego o średniej 0 i wariancji 1
# przemnożenie przez odchylenie standandardowe sigma i dodanie śreniej mi
# transformuje rozkład do rozkładu normalnego o średniej mi i wariancji sigma**2
n, bins, patches = plt.hist(x, 50, density=True,
facecolor='green', edgecolor='black', alpha=0.75)
# Tu w jawny sposób odbieramy zwracane przez plt.hist obiekty
# Zmieniamy też:
# - ilość binów na 50
# - normujemy histogram do jedności
# - ustalamy kolor prostokątów na zielony
# - ustawiamy (nie)przezroczystość prostokątów na 0.75
bincenters = 0.5*(bins[1:]+bins[:-1])
# wytwarzamy array z centrami binów korzystając z granic binów
# zwróconych przez plt.hist w macierzy bins
y = norm.pdf( bincenters, mi, sigma)
# obliczamy wartości w normalnym rozkładzie gęstości prawdopodobieństwa
# o średniej mi i wariancji sigma**2 dla wartości bincenters
l = plt.plot(bincenters, y, 'r--', linewidth=1)
# do histogramu dorysowujemy linię
plt.show()
Krzywa parametryczna
Rysowanie krzywej danej w postaci parametrycznej niewiele się różni od rysowania wykresu funkcji. Żeby było zabawniej, wykonam jeszcze przy okazji rachunek Monte Carlo oraz jego wizualizację.
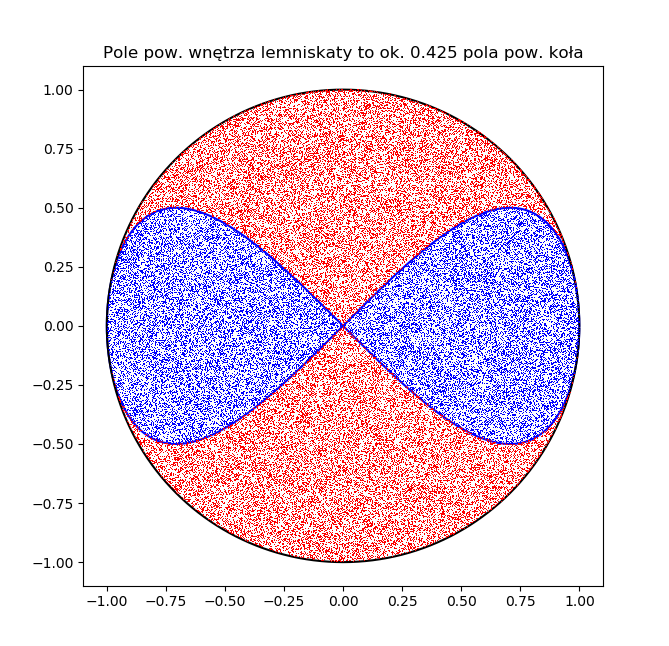
Krzywa, jaką tutaj narysujemy to tzw. lemniskata Gerona. Zostanie dodatkowo opisana okręgiem jednostkowym; następnie, wylosuję dużą liczbę punktów o równomiernym rozkładzie leżących w kwadracie opisanym na tym okręgu. Robię tak, ponieważ łatwo mi jest wylosować tablicę wielu liczb z zakresu (0, 1) — jest do tego gotowa funkcja numpy.random.random, następnie przeskalować i przesunąć je do odcinka (-1, 1). Wreszcie, traktując je jako pary współrzędnych (x, y), pozostawiam tylko te, które znalazły się we wnętrzu koła jednostkowego (odrzucając pozostałe), i dzielę na te, które znalazły się w obszarze wewnątrz lemniskaty, i te, które znalazły się na zewnątrz.
Intuicyjnie jest dość jasne, że — o ile losowaliśmy punkty rzeczywiście w sposób równomierny — stosunek liczby „trafień" w obszar ograniczony lemniskatą do liczby wszystkich „trafień" w obszar koła będzie w przybliżeniu równy stosunkowi pól powierzchni tych obszarów. I na tym tu poprzestaniemy; to, jak dokładne to może być przybliżenie, czyli jakiej wielkości błędu możemy oczekiwać, to już problem na inne zajęcia...
import numpy as np
import matplotlib.pyplot as plt
Φ = np.arange(0, 2*np.pi, 2*np.pi/600)
X = np.cos(Φ)
Y = np.sin(2*Φ) / 2 # = np.sin(Φ) * np.cos(Φ)
plt.axes(aspect='equal') # to mi gwarantuje, że okrąg nie wyjdzie „spłaszczony"
plt.plot(X, Y, 'b')
YO = np.sin(Φ)
plt.plot(X, YO, 'k')
# biorę całą kupę losowych punktów z przedziału (-1, 1)
P = np.random.random((100000, 2)) * 2 - 1 # milion par (x, y)
# wyrzucam te, które są poza kołem x**2 + y**2 < 1
P = P[(P**2).sum(axis=1) < 1]
# dzielę na te co wewnątrz lemniskaty, i te co na zewnątrz
I_in = np.abs(P[:,1]) < np.abs(P[:,0]) * np.sqrt(1 - P[:,0]**2)
P_in = P[I_in]
P_out = P[~I_in]
# maluję wewnętrzne na niebiesko
plt.plot(P_in[:,0], P_in[:,1], 'b,')
# a zewnętrzne na czerwono
plt.plot(P_out[:,0], P_out[:,1], 'r,')
# powierzchnia to z grubsza stosunek l. punktów wewnętrznych do wszystkich
S = P_in.size / P.size
plt.title('Pole pow. wnętrza lemniskaty to ok. {:.3f} pola pow. koła'.format(S))
plt.show()
Przy okazji, jak widać w kodzie Pythona (wersja 3) można bezproblemowo używać liter z innych alfabetów, nie tylko łacińskiego. Niestety nie wszystkie systemy operacyjne zapewniają bezproblemową obsługę pełnego zestawu liter wszelkich języków, dlatego na ogół wykorzystywanie liter z egzotycznych systemów pisma nie jest szczególnie zalecane.
W wyniku uruchomienia tego programu powinno pojawić się okno z obrazkiem podobnym do poniższego:
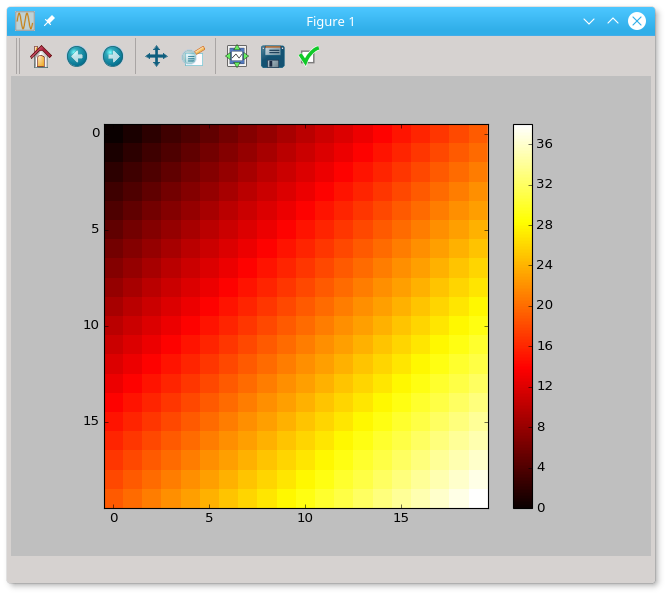
Wizualizacja zawartości tablicy dwuwymiarowej
import numpy as np
import matplotlib.pyplot as plt
A = np.arange(20)
X, Y = np.meshgrid(A, A)
Z = X + Y
plt.imshow(Z, cmap='hot', interpolation='none')
plt.colorbar()
plt.show()
Wynik:
Jak można się domyślić, parametr cmap wywołania funkcji imshow odpowiada za odwzorowanie pomiędzy wartościami elementów tablicy a barwami - jest wiele predefiniowanych takich odwzorowań (colormaps), opisanych w dokumentacji. Za pomocą wartości 'none' parametru interpolation wyłączyliśmy ,,wygładzanie" obrazu, inne możliwe wartości umożliwiają wybór różnych algorytmów wygładzania. Wywołanie colorbar dostarcza paska wizualizującego odpowiedniość pomiędzy wartościami liczbowy i barwami.
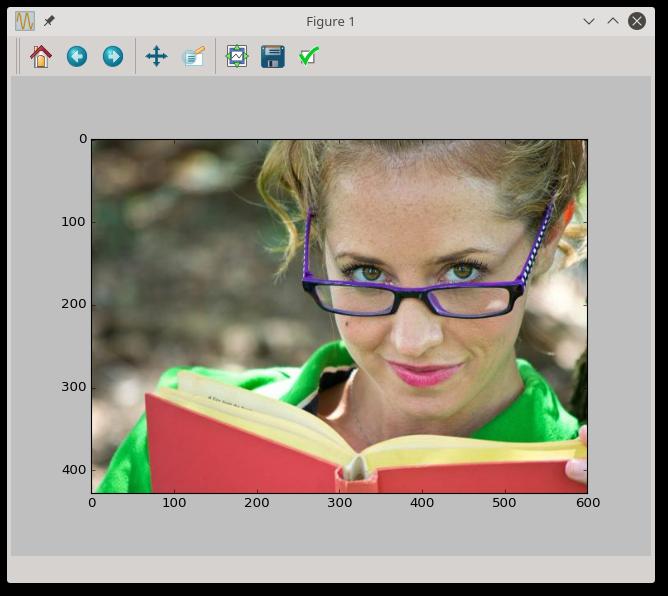
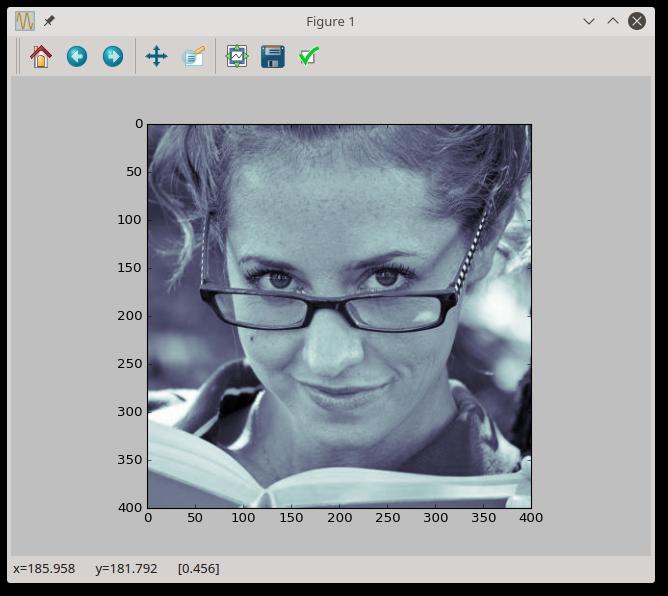
Plik graficzny jako źródło danych
import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('reading-girl.jpg')
plt.imshow()
plt.show()
Wynik:
Wynikiem wywołania imread jest tablica o kształcie (wysokość, szerokość, 3) zawierająca dla każdego piksela obrazu wartości jego składowych RGB, tj. natężeń barw: czerwonej, zielonej, i niebieskiej - jako liczby w zakresie od 0 do 255 włącznie. Oczywiście na tej tablicy możemy wykonywać najróżniejsze operacje, analizując treść obrazu czy przekształcając go. Przykładowo:
img1 = img[:400, -400:] # przycinam obraz do kształtu 400x400 pikseli
img2 = img1.sum(axis=2)
img3 = img2 / img2.max()
plt.imgshow(img3, cmap='bone')
plt.show()
Wynik:
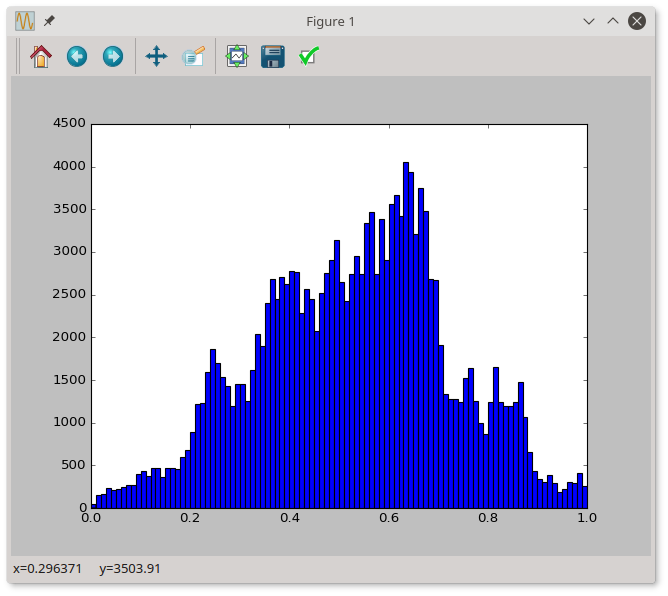
plt.hist(img3.flatten(), bins=100)
plt.show()
Wynik:
Wykonaliśmy w ten sposób histogram opisujący rozkład natężenia pikseli obrazka.
Wiele wykresów w jednym oknie
Ćwiczenia
1. Spróbuj znaleźć sposób przekształcenia obrazka takiego, jak poniższy portret autora skryptu:
do postaci przypominającej
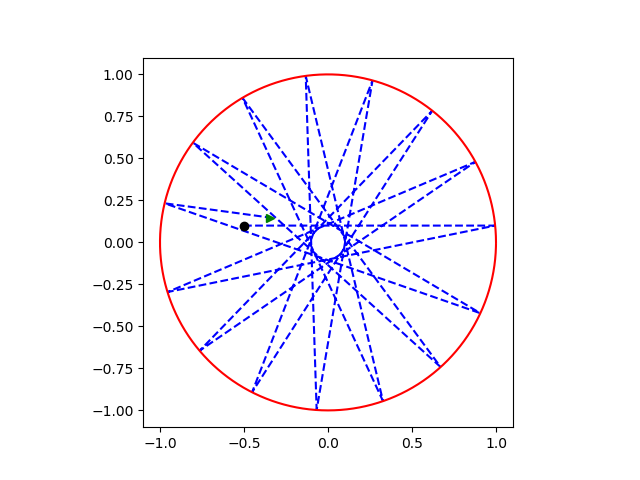
2. (Nieco złożone) Napisz program symulujący „bilard na kółku". Dokładniej: wewnątrz koła jednostkowego na płaszczyźnie porusza się cząstka (punkt), zachowując stałą prędkość — dopóki nie napotka brzegu, czyli okręgu; wówczas odbija się zgodnie z zasadą, że kąt padania równa się kątowi odbicia; chodzi o kąt pomiędzy wektorem prędkości a promieniem okręgu jednostkowego w miejscu, gdzie tor ruchu przecina się z okręgiem, po odbiciu jest on taki sam co do wartości ale po drugiej stronie promienia. Program rysuje okręg jednostkowy oraz tor ruchu cząstki wewnątrz tego okręgu, w zależności od początkowego położenia, kierunku początkowej prędkości (wartość prędkości jest nieistotna, ponieważ jest stała), i czasu obserwacji.
Wynikiem programu są wykresy podobne do poniższego:
czarną kropką oznaczono położenie początkowe, a na zielono — końcowe.