Pochodne
Podstawowe definicje
Iloraz różnicowy funkcji
Def. Niech funkcja [math]f\;[/math] będzie określona w pewnym przedziale otwartym zawierającym punkt [math]a\;[/math]. Ilorazem różnicowym funkcji [math]f\;[/math] w punkcie [math]a\;[/math] dla przyrostu [math]h\;[/math] nazywamy funkcję
Pochodna funkcji [math]f[/math] w punkcie [math]a[/math]
Pochodną funkcji [math]f\;[/math] w punkcie [math]a\;[/math] (ozn. [math]f'(a)[/math]) nazywamy granicę ilorazu różnicowego:
Inne oznaczenia pochodnej
Pochodną funkcji [math]f\;[/math] w punkcie [math]a\;[/math] oznacza się też:
bądź — jeśli nie trzeba podawać, w jakim punkcie jest liczona — jako [math]\frac{df(x)}{d x}\;[/math].
Oznaczenia [math]\frac{df(x)}{d x}\;[/math] pochodzą od Leibniza (XVII w.) — jednego z wynalazców (obok Newtona) rachunku różniczkowego. Pochodzenie tej symboliki jest następujące: Iloraz różnicowy (1) można zapisać jako:
pochodna jest granicą ilorazu różnicowego, i "w granicy" zastępuje się [math]\Delta\;[/math] przez [math]d\;[/math].
Uwaga
Symbol [math]\frac{df(x)}{d x}\;[/math] należy traktować jako jedną całość. O ile wielkości z licznika czy mianownika — tzn [math]\Delta f\;[/math] czy [math]\Delta x\;[/math] są dobrze określone, o tyle oddzielnie symbole [math]df\;[/math], [math]d x\;[/math] — bez dodatkowych umów — nie mają sensu, lub są bezużyteczne. (gdyby np. rozpatrywać je w najbardziej narzucający się sposób, tzn. jako granice, gdy przyrost argumentu dąży do zera, to otrzymałoby się zero). Sensowna, bądź użyteczna, jest jedynie ich kombinacja [math]\frac{df}{dx}\;[/math].
Nie oznacza to, że nie wolno w ogóle posługiwać się symbolami w rodzaju [math]d f\;[/math] czy [math]d x\;[/math]. Wolno, ale jedynie na etapie pośrednim jakiegoś rozumowania, którego finałem będzie jakiś w pełni legalny już symbol w rodzaju [math]\frac{df}{d x}\;[/math] czy [math]\int f(x) d x\;[/math].
Przykład
[math]f(x)=x^2\;[/math], [math]f'(3)=6\;[/math].
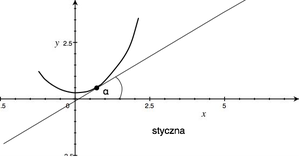
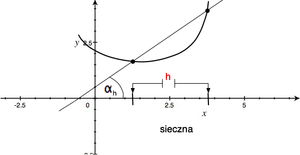
Pochodna funkcji w punkcie ma bardzo wyrazisty sens geometryczny. (RYS.) Rozpatrzmy wykres funkcji [math]y=f(x)\;[/math]. Ustalmy dodatnie [math]h\;[/math] i przeprowadźmy prostą przez punkty: [math](x, f(x))\;[/math] i [math](x+h, f(x+h))\;[/math]. Prostą taką nazywamy sieczną krzywej. Jak widać, iloraz różnicowy jest tangensem kąta [math]\alpha_h\;[/math], który sieczna tworzy z osią [math]OX\;[/math]. Gdy [math]h\to 0\;[/math], to sieczne dążą do prostej granicznej — stycznej do krzywej w punkcie [math]x\;[/math]. Tak więc
[math] f'(a)=\tg \alpha [/math]
Nie każda funkcja ciągła posiada pochodną (co w ilustracji geometrycznej znaczy, że nie każda krzywa posiada styczną, a jeśli nawet tak, to taka styczna nie jest jednoznacznie określona). I tak np. funkcja [math]f(x)=|x|\;[/math] nie posiada pochodnej w punkcie [math]x=0\;[/math]. Mamy bowiem:
W powyższym jednak przypadku możemy mówić o pochodnych jednostronnych, tzn. granicach ilorazów różnicowych: [math]\lim_{h \to 0^+}\;[/math] (pochodna prawostronna) i [math]\lim_{h \to 0^-}\;[/math] (pochodna lewostronna). Dokładniej, mamy:
Pochodna jednostronna
Pochodną prawostronną (lewostronną) funkcji [math]f\;[/math] w punkcie [math]a\;[/math] nazywamy granicę
Są jednak też funkcje, które (w jakimś punkcie) w ogóle nie posiadają pochodnej — ani lewo-, ani prawostronnej. Np. funkcja:
[math] f(x)=x \sin\frac{1}{x} \;\;\;{\rm dla} \;\;\;x\ne 0;\;\;\;\;\; f(0)=0 [/math]
jest ciągła, lecz nie posiada pochodnej (ani lewo-, ani prawostronnej) w zerze. Nieistnienie tej pochodnej wynika np. z nieistnienia granicy [math]\displaystyle\mathop{\lim}_{x\to 0}\,\sin\frac{1}{x}\;[/math]. Bowiem granica ilorazu różnicowego:
nie istnieje, jak to widzieliśmy uprzednio (http://brain.fuw.edu.pl/edu/Matematyka:Funkcje_i_granice#Funkcje_bez_jednostronnych_granic). Istnieją także funkcje ciągłe, które nie posiadają pochodnej w żadnym punkcie. Rozważamy też pochodne nieskończone (ma to miejsce, gdy granica ilorazu różnicowego w jakimś punkcie dąży do nieskończoności). I tak np. dla funkcji [math]f(x)=\sqrt{x}\;[/math] mamy
(bo [math]\lim_{h \to 0} \sqrt{h}=0\;[/math]); bądź dla pochodnej dwustronnej: weźmy [math]f(x)=\sqrt[3]{x}\;[/math],
Różniczkowalność
Mówimy, że funkcja jest różniczkowalna w przedziale otwartym, jeśli posiada pochodną skończoną w każdym punkcie tego przedziału. Funkcja jest różniczkowalna w przedziale domkniętym [math][a,b]\;[/math], jeśli posiada pochodną w każdym punkcie wewnętrznym przedziału, a pochodną jednostronną (prawą lub lewą) w lewym lub prawym końcu przedziału.
Ciągłość pochodnej w przedziale
Mówimy, że pochodna [math]f'(x)\;[/math] funkcji [math]f(x)\;[/math] jest ciągła w przedziale [math][a,b]\;[/math], jeśli [math]f'(x)\;[/math] jest ciągła wewnątrz przedziału, pochodna prawostronna jest ciągła prawostronnie w punkcie [math]a\;[/math], zaś pochodna lewostronna — ciągła lewostronnie w punkcie [math]b\;[/math].
Pierwsze zastosowania geometryczne i fizyczne pochodnej
Normalna
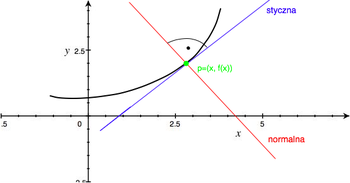
Przez normalną do krzywej [math]y=f(x)\;[/math] w punkcie [math]p=(x, f(x))[/math] rozumiemy prostą, prostopadłą do stycznej w [math]p\;[/math] i przechodzącej przez [math]p\;[/math].
Tak więc:
- równanie prostej stycznej do krzywej [math]y=f(x)\;[/math] w punkcie [math]p=(x_0, y_0)\;[/math], gdzie [math]y_0=f(x_0)\;[/math] jest:
[math] y=f'(x_0) x + f(x_0) - f'(x_0) x_0, \;[/math] lub — w postaci być może łatwiejszej do zapamiętania —
[math] y-y_0 = f'(x_0)(x-x_0). [/math] - Dla prostej normalnej mamy: Współczynni kierunkowy tej prostej to
[math]-\frac{1}{f'(x_0)}\;[/math], co daje równanie prostej
[math] y=-\frac{1}{f'(x_0)} x + y_0 +\frac{x_0}{f'(x_0)} \;[/math] lub w równoważnej postaci
[math] f'(x_0) (y-y_0) = -(x-x_0). [/math]
W fizyce, znaczeniem pochodnej jest prędkość (zmiany jakiejś wielkości fizycznej w czasie). I tak, prototypem wszelkich takich wielkości jest droga (punktu materialnego jako funkcja czasu). Pochodna drogi po czasie — to właśnie prędkość. Analogicznie definiuje się inne rodzaje prędkości.
Np. gdy mamy rozpad promieniotwórczy substancji radioaktywnej, to możemy mówić o szybkości rozpadu (prędkości ubytku masy substancji radioaktywnej).
Różniczkowanie funkcji elementarnych
Zauważmy najsampierw, że jest prawdziwe
Twierdzenie
Jeśli funkcja [math]f\;[/math] jest różniczkowalna w punkcie [math]x\;[/math], to jest w tym punkcie ciągła.
Dowód
Skoro [math]f\;[/math] jest różniczkowalna w punkcie [math]x\;[/math], to istnieje i jest skończona granica ilorazu różnicowego
tak więc
co oznacza, że [math]f\;[/math] jest ciągła w punkcie [math]x\;[/math]. CBDO
Twierdzenie
Pochodna funkcji stałej: [math]f(x)=c\;[/math] jest równa [math]0\;[/math]:
Dowód
Bowiem: [math]f(x+h)=c\;[/math], [math]f(x)=c\;[/math], co daje
CBDO
Twierdzenie
Pochodna funkcji identycznościowej [math]f(x)=x\;[/math] jest równa 1:
Dowód
Mamy:
Twierdzenie
Mamy następujące wzory dotyczące różniczkowania sumy, różnicy, iloczynu i ilorazu funkcji różniczkowalnych. Jeśli [math]f(x)\;[/math], [math]g(x)\;[/math] są różniczkowalne w punkcie [math]x\;[/math], to mamy
Dowód
- dla (8) (dla sumy):
[math] (f(x)+ g(x))' =\lim_{h \to 0}\frac{(f(x+h)+g(x+h)) - (f(x)+g(x))}{h} [/math] [math] = \lim_{h \to 0}\frac{f(x+h) - f(x)}{h} + \lim_{h \to 0}\frac{g(x+h) - g(x)}{h} = f'(x)+g'(x); [/math] dla różnicy dowód jest analogiczny. - dla (9)
[math] (f(x)\cdot g(x))' =\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h) - f(x)\cdot g(x)}{h} [/math] [math] (f(x)\cdot g(x))' =\lim_{h \to 0}\frac{(f(x+h)\cdot g(x+h) - f(x+h)\cdot g(x)) + ( f(x+h)\cdot g(x) - f(x)\cdot g(x))}{h} [/math] [math] = \lim_{h \to 0} f(x+h) \frac{g(x+h) - g(x)}{h} + \lim_{h \to 0}g(x)\frac{f(x+h) - f(x)}{h} = f'(x)\cdot g(x)+g'(x)\cdot f(x). [/math] - dla (10).
Pokażemy najsampierw:
[math] \frac{d\left(\frac{1}{f(x)}\right)}{d x} = -\frac{1}{f^2(x)}\frac{d f(x)}{d x}. [/math]
Mamy bowiem:
[math] \frac{d\left(\frac{1}{g(x)}\right)}{d x} =\lim_{h \to 0}\left( \frac{\frac{1}{g(x+h)}-\frac{1}{g(x)}}{h}\right)= [/math] [math] -\frac{1}{\lim_{h \to 0} g(x+h)}\cdot \frac{1}{g(x)} \cdot\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}=-\frac{1}{g^2(x)}\cdot\frac{dg(x)}{dx}, [/math]bo [math]\lim_{h \to 0} g(x+h)=g(x)\;[/math]; i ponadto, ponieważ [math]g(x)\ne 0\;[/math], to istnieje takie [math]\delta\gt 0\;[/math], że dla [math]|h|\lt \delta\;[/math] zachodzi [math]g(x+h)\ne 0\;[/math], tak więc wszystkie wyrażenia w (12) są dobrze określone.
Teraz (10) wynika z (9) oraz (11): [math] \left(f(x)\frac{1}{g(x)} \right)' = f'(x)\cdot \frac{1}{g(x)} + f(x)\cdot\left(-\frac{1}{g^2(x)} \right)= \frac{ f'(x)g(x)-g'(x)f(x)}{g^2(x)}.[/math]
Wniosek
Podstawiając we wzorach (8) oraz (9): [math]f(x) = c\;[/math], otrzymamy:
Wzór (13) mówi, że przesunięcie wykresu funkcji [math]f(x)\;[/math] wzdłuż osi [math]0Y\;[/math] nie ma wpływu na wartość kąta, tworzonego przez styczną z osiami. Wzór (14) natomiast mówi, że jeżeli przeskalujemy wykres funkcji [math]y=f(x)\;[/math] [math]c\;[/math] razy, to tyle samo razy zwiększy się tangens kąta nachylenia stycznej.
Twierdzenie
Dowód
Dowodzi się indukcyjnie. Dla [math]n=0\;[/math] i [math]n=1\;[/math] wzór ten jest prawdziwy — p. (6) i (7). Załózmy teraz, że wzór jest prawdziwy dla [math]n-1\;[/math], i mamy dla [math]n\;[/math], z wykorzystaniem (9)
CBDO
Twierdzenie
Dowód
Weźmy teraz [math]n\lt 0\;[/math]. Mamy, z (12) i (15)
CBDO
Uwaga
Wzór ten słuszny jest też dla dowolnych wykładników rzeczywistych, co udowodnimy nieco później.
Z pokazanych właśnie faktów wynika od razu
Twierdzenie (wzór na pochodną wielomianu)
Twierdzenie
Dowód
Twierdzenie
Dowód
[math] =-\lim_{h \to 0}\frac{\sin(\frac{h}{2})}{\frac{h}{2}}\cdot \lim_{h \to 0} \sin(x+\frac{h}{2}) =\sin x [/math]
Twierdzenie
[math] (\tg x)'=\frac{1}{\cos^2 x}. [/math]
Dowód
Twierdzenie
[math](\ln x)' = \frac{1}{x} \;\;\;\mbox{i ogolniej}\;\;(\log_a x)'=\frac{1}{x\ln a}\;[/math].
Dowód
Podstawmy teraz [math]y=\frac{h}{x}\;[/math]. Ponieważ [math]\lim_{h \to 0} y=0\;[/math], to
Mamy: [math]\lim_{y \to 0} (1+y)^\frac{1}{y}=e.\;[/math] Pamiętając, że logarytm jest funkcją ciągłą wszędzie w dziedzinie, a w szczególności dla wartości argumentu równej [math]e\;[/math], mamy
zatem
Drugą część twierdzenia otrzymamy z własności logarytmu: