Twierdzenia o splocie i o próbkowaniu (aliasing): Różnice pomiędzy wersjami
| Linia 129: | Linia 129: | ||
Splot ma ponadto własność łączności -- dowód można znaleźć np. tutaj: http://planetmath.org/convolutionassociativityof | Splot ma ponadto własność łączności -- dowód można znaleźć np. tutaj: http://planetmath.org/convolutionassociativityof | ||
| − | + | ||
Let <math>f</math>, <math>g</math>, and <math>h</math> be measurable functions on the reals, and | Let <math>f</math>, <math>g</math>, and <math>h</math> be measurable functions on the reals, and | ||
suppose the convolutions <math>(f*g)*h</math> and <math>f*(g*h)</math> exist. We must show | suppose the convolutions <math>(f*g)*h</math> and <math>f*(g*h)</math> exist. We must show | ||
that <math>(f*g)*h = f*(g*h)</math>. By the definition of convolution, | that <math>(f*g)*h = f*(g*h)</math>. By the definition of convolution, | ||
| − | <center><math> | + | <center><math> |
((f*g)*h)(u) | ((f*g)*h)(u) | ||
| − | + | = \int_{\mathbb{R}} (f*g)(x) h(u-x)\,dx | |
| − | + | = \int_{\mathbb{R}} \left[ \int_{\mathbb{R}} f(y) g(x-y)\,dy\right] h(u-x)\,dx | |
| − | + | = \int_{\mathbb{R}} \int_{\mathbb{R}} f(y) g(x-y) h(u-x)\,dy\,dx. | |
| − | + | </math></center> | |
By Fubini's theorem we can switch the order of integration. Thus | By Fubini's theorem we can switch the order of integration. Thus | ||
| − | <center><math> | + | <center><math> |
((f*g)*h)(u) | ((f*g)*h)(u) | ||
| − | + | = \int_{\mathbb{R}} \int_{\mathbb{R}} f(y) g(x-y) h(u-x)\,dx\,dy | |
| − | + | = \int_{\mathbb{R}} f(y) \left[\int_{\mathbb{R}} g(x-y) h(u-x)\,dx\right]\,dy. | |
| − | + | </math></center> | |
Now let us look at the inner integral. By translation invariance, | Now let us look at the inner integral. By translation invariance, | ||
| − | <center><math> | + | <center><math> |
\int_{\mathbb{R}} g(x-y) h(u-x)\,dx | \int_{\mathbb{R}} g(x-y) h(u-x)\,dx | ||
| − | + | = \int_{\mathbb{R}} g((x+y)-y) h(u-(x+y))\,dx | |
| − | + | = \int_{\mathbb{R}} g(x) h((u-y)-x)\,dx | |
&= (g*h)(u-y). | &= (g*h)(u-y). | ||
| − | + | </math></center> | |
So we have shown that | So we have shown that | ||
<center><math> | <center><math> | ||
| Linia 163: | Linia 163: | ||
which by definition is <math>(f*(g*h))(u)</math>. Hence convolution is associative. | which by definition is <math>(f*(g*h))(u)</math>. Hence convolution is associative. | ||
| − | + | ||
Wersja z 10:10, 4 paź 2015
AS/ Twierdzenie o splocie
Korelacja i splot
Korelacja jest miarą podobieństwa lub wzajemnej zależności. Jeśli mówimy, że występuje korelacja między wydajnością i ceną komputerów, to mamy na myśli stwierdzenie, że droższe komputery mają zwykle większą moc obliczeniową — im mniej przypadków przeciwnych, tym korelacja silniejsza. Silna korelacja sygnałów [math]x[/math] i [math]y[/math] oznacza, że wzrostowi [math]x[/math] towarzyszy najczęściej wzrost [math]y[/math] [math]\left( x_\nearrow\; \rightarrow y_\nearrow \right)[/math]. Jeśli przeważa sytuacja odwrotna [math]\left( x_\nearrow\; \rightarrow y_\searrow \right)[/math] mówimy o korelacji ujemnej.
Miarą współzmienności (kowariancji) dwóch sygnałów jest ich iloczyn. Przed obliczeniem tego iloczynu (w ogólnym przypadku mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć wartość średnią:
[math] \sigma_{x y}=\int \left(x(t)-\bar{x}\right)\left(y(t)-\bar{y}\right) dt [/math]
Dzięki temu w przypadku, gdy sygnały są od siebie niezależne, [math]\sigma_{x y}[/math] będzie bliska zeru — uniezależnia to miarę kowariancji od wartości średnich sygnałów. Aby otrzymać wartości z przedziału [math][ -1, 1 ][/math] wprowadzamy jako czynnik normalizacyjny wariancję sygnału:
[math] \sigma^2_s=\int\left( s(t)-\bar{s}\right)^2 dt [/math]
Znormalizowaną w ten sposób kowariancję zwiemy korelacją:
[math] \mathrm{korelacja}_{x y} = \frac{\sigma_{x y}}{\sqrt{\sigma^2_x\sigma^2_y}} [/math]
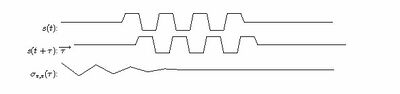
Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte względem siebie w czasie. W wykryciu takiej sytuacji pomaga funkcja korelacji wzajemnej, czyli korelacja dwóch sygnałów w funkcji ich wzajemnego przesunięcia. Z kolei autokorelacja to miara korelacji sygnału [math]s(t)[/math] z jego kopią przesuniętą o [math]\tau[/math]. Pomijając normalizację i odejmowanie średnich otrzymamy
[math] \sigma_{s, s}(\tau)=\int s(t) s(t+\tau) dt [/math]
Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie innych maksimów związane jest z występowaniem w sygnale okresowo powtarzających się zjawisk. Twierdzenie Wienera-Chinczyna mówi wręcz, że widmo mocy obliczać możemy jako transformatę Fouriera funkcji autokorelacji.
[math] \mathrm{corr}\left(x(t),y(t)\right) = \frac{\sigma^2_{x y}}{\sigma_x \sigma_y} = \frac{\int (x(t)-\mu_x)( y(t)-\mu_y) dt } {\sqrt{ \int (x(t)-\mu_x)^2 dt \int (y(t)-\mu_y)^2 dt }} [/math]
lub
[math] \frac{\sum_i (x_i-\mu_x)(y_i-\mu_y)} {\sqrt{\sum_j (x_j-\mu_x)^2 \sum_k (y_k-\mu_y)^2}} [/math]
Rozważmy transformatę Fouriera funkcji korelacji sygnałów [math]f[/math] i [math]g[/math], dla uproszczenia pomijając normalizację: [math] s(\tau)=\int f(t) g(t+\tau) dt [/math]
[math] =\int e^{-i\omega (t+\tau)} g(t+\tau) \int e^{i\omega t} f(t) dt \; du [/math]
[math] = \int e^{-i\omega u} f(u) du \int e^{i\omega(t)} g(t) dt = \hat{f}(\omega) \overline{\hat{g}(\omega)} [/math]Jak widać, operator korelacji odpowiada w przestrzeni transformat Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem zespolonym transformaty drugiego.
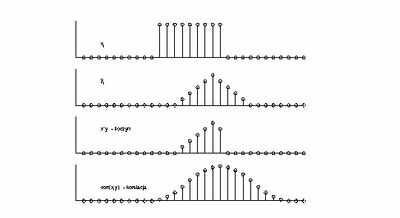
Twierdzenie o splocie
... czyli splot w przestrzeni czasu odpowiada iloczynowi w przestrzeni transformat Fouriera.
Jest to wynik wygodniejszy od wzoru (1), stąd filtrowanie realizowane jest właśnie z pomocą splotu, który jak widać z równania (1) jest korelacją z sygnałem o odwróconym kierunku czasu.
Dowód:
[math] \hat{s}(\omega) = \int_{-\infty}^{\infty} e^{-i \omega t} s(t) d t = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-i \omega t} f(u) g(t-u) \,d u \,d t [/math] [math] = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{-i \omega (t-u)}g(t-u) dt \right) du [/math]
Całka w nawiasie przebiega od [math]-\infty[/math] do [math]\infty[/math], więc możemy zamienić [math](t-u)[/math] na [math]t[/math]:
[math] = \int_{-\infty}^{\infty} e^{- i \omega u} f(u) \left( \int_{-\infty}^{\infty} e^{i \omega t}g(t) dt \right) du = \hat{f}(\omega) \hat{g}(\omega) [/math]
Splot ma ponadto własność łączności -- dowód można znaleźć np. tutaj: http://planetmath.org/convolutionassociativityof
Let [math]f[/math], [math]g[/math], and [math]h[/math] be measurable functions on the reals, and
suppose the convolutions [math](f*g)*h[/math] and [math]f*(g*h)[/math] exist. We must show
that [math](f*g)*h = f*(g*h)[/math]. By the definition of convolution,
By Fubini's theorem we can switch the order of integration. Thus
Now let us look at the inner integral. By translation invariance,
So we have shown that
which by definition is [math](f*(g*h))(u)[/math]. Hence convolution is associative.