Uczenie maszynowe i sztuczne sieci neuronowe/Ćwiczenia 11

Uczenie_maszynowe_i_sztuczne_sieci_neuronowe_cw/Uczenie bez nadzoru

Algorytm k-means

Algorytm k-means jest zaimplementowany w module scipy.cluster.vq (vq: vector quantization) ([dokumentacja]). Mamy tam funkcję

kmeans(obs, k_or_guess, iter=20, thresh=1e-05) 

optymalizującą położenia centroidów, oraz pomocniczą funkcję

vq

przypisującą poszczególne obserwacje do skupisk reprezentowanych przez centroidy.

Przed zapuszczeniem algorytmu k-means na danych dobrze jest przeskalować każdą z cech w macierzy wejściowej, tak aby miała jednostkową wariancję. Można to zrobić za pomoca funkcji whiten.

Przykładowy kod.

Kod ten pokazuje jak:

• wygenerować symulowane dane
• przeskalować je, tak aby miały jednostkową wariancję w każdej z cech.
• podzielić je na dwa skupiska
• zilustrować wynik

from pylab import plot,show
from numpy import vstack,array
from numpy.random import rand
from scipy.cluster.vq import kmeans,vq,whiten

# generujemy dane: 
# - 150 dwuwymiarowych punktów z rozkładu jednorodnego ze średnią (1,1)
# - 150 dwuwymiarowych punktów z rozkładu jednorodnego ze średnią  (0.5,0.5)

data = vstack((rand(150,2) + array([.5,.5]),rand(150,2)))
data =  whiten(data)
# policz K-Means dla  K = 2 (2 skupiska)
centroids,_ = kmeans(data,2)
# przypisz wektory wejściowe do skupisk
idx,_ = vq(data,centroids)

# narysuj wyniki
plot(data[idx==0,0],data[idx==0,1],'ob',
     data[idx==1,0],data[idx==1,1],'or')
plot(centroids[:,0],centroids[:,1],'sg',markersize=8)
show()

Segmentacja obrazu algorytmem k-means

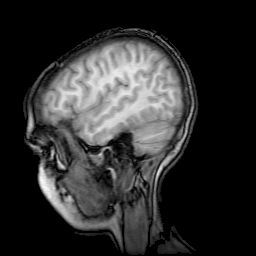
W tym ćwiczeniu zapoznamy się z zastosowaniem algorytmu analizy skupień do segmetacji obrazu. Segmentacja tegotypu może stanowic etap wstępnego przetwarzania na potrzeby np. detekcji obiektów lub klasyfikacji. W zadaniu tym zapoznamy sie także z metodą dobierania atumatycznie ilości skupisk.

Obrazek na którym będziemy pracować, proszę go zapisać w bieżącym katalogu:

Najpierw importujemy i oglądamy obrazek:

from pylab import plot,show,figure,imshow,cm, imread, axis
import numpy as np
from scipy.cluster.vq import kmeans,vq

im = imread('Skan.png')
# Oryginalny obrazek miał przestrzeń barwną RGB.
# Spłaszczamy przestrzeń barwną obrazka
im = im.mean(axis=2)
#oglądamy obrazek
imshow(im, cmap=cm.gray)
axis('off')
show()
imshow(im, cmap=cm.gray)
axis('off')
show()

Teraz zamieniamy rysunek (dwuwymiarowa tablica 256x256) na wektor (o długości 256*256 )

data = im[:]
data.shape = 256*256,1

Teraz będziemy próbować podzielić ten wektor na skupiska (w liczbie od 2 do 9). Dla każdej konkretnej ilości skupisk obliczamy dwie wielkości:

[math]J_{intra}(K)[/math] - to jest miara odległości wewwnątrz centrów: równanie na J

[math]J_{inter}(K) = \min_{j\lt i} \sqrt{ (\mu_i -\mu_j)^T(\mu_i - \mu_j)} [/math] : to najmniejsza odległości między centrami

K_max = 9
J_inter = np.ones(K_max)*1e16
J_intra = np.zeros(K_max)
centroids =[]
for K in range(2,K_max):
    trial =0
    while (len(centroids)<K)&(trial<20):
        centroids,J_intra[K] = kmeans(data,K)
        trial+=1
    print 'K: ',K, len(centroids)
    for ki in range(len(centroids)):
        for kj in range(ki):
            print ki, kj
            print centroids[ki]
            print centroids[kj]
            ################
## dopisz kod obliczający odległość między centrami i oznacz ją d
            ################
            # jeśli uzyskana odległość jest mniejsza niż dotychczas zapamiętana to ją zapamiętujemy:
            if J_inter[K]>d:
                J_inter[K]=d
    print K, J_intra[K],J_inter[K]

Wykreślamy stosunek [math],J_{intra}/J_{inter}[/math] i znajdujemy K dla którego jest najmniejszy:

figure(1)
plot(range(2,K_max),J_intra[2:]/J_inter[2:])
K_opt = np.argmin(J_intra[2:]/J_inter[2:])+2

print K_opt

Dla tej optymalnej ilości skupisk znajdujemy położenia centrów i przypisujemy klasę dla każdego punktu danych:

centroids,J_intra[K] = kmeans(data,K_opt)

# przypisujemy klasę
idx,_ = vq(data,centroids)

Formatujemy wektor w obrazek i podziwiamy efekt:

idx.shape = 256,256
figure(2)
imshow(idx, cmap=cm.gray)

show()

Dla porównania proszę wykreślić histogram odcieni szarości dla wekotra data.

Algorytm EM: implementacja

W celu zapoznania się z algorytmem EM zaimplementujemy go.

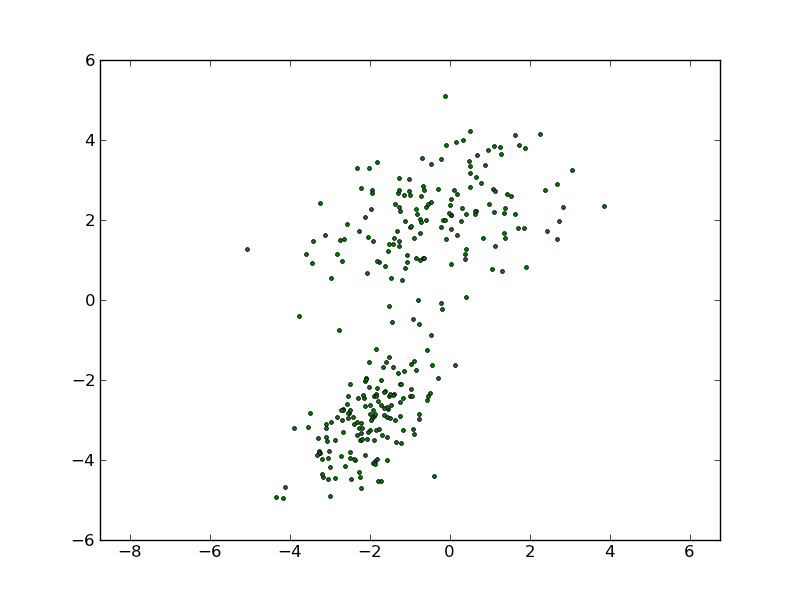
Program, który powstanie po uzupełnieniu kodu powinien ilustrować dopasowywanie modelu EM do danych będzących sumą dwóch rozkładów gaussowskich:

Funkcje pomocnicze

Najpierw standardowe importy i kilka funkcji pomocniczych:

# -*- coding: utf-8 -*-
import matplotlib
matplotlib.use('TkAgg')
import pylab as py
import random, copy
import numpy as np
import sys


def pnorm(x, m, s):
    """
    Oblicza gęstość wielowymiarowego rozkładu normalnego dla punktów
    w wektorze x
    Parametry rozkładu :
    m - średnia
    s- macierz kowariancji
    dla zwiększenia czytelności kodu stosujemy typ matrix
    """
    xm = np.matrix(x-m)
    xmt = np.matrix(x-m).transpose()
    for i in xrange(len(s)): # zabezpieczenie dla większej stabliności numerycznej
        if s[i,i] <= sys.float_info[3]: # min float
            s[i,i] = sys.float_info[3]
    sinv = np.linalg.inv(s)

    return (2.0*np.pi)**(-len(x)/2.0)*(1.0/np.sqrt(np.linalg.det(s)))\
            *np.exp(-0.5*(xm*sinv*xmt))

def draw_params(t,nbclusters):
        '''funkcja do losowania parametrów początkowych
        t - zbiór treningowy
        '''
        nbobs,nbfeatures = t.shape
        # inicjuje średnie przez losowanie punktu ze zbioru danych
        tmpmu = np.array([t[random.uniform(0,nbobs),:]],np.float64)
        # kowariancje inicjowane są jako macierze diagonalne , wariancja dla każdej cechy inicjowana jest jako wariancja tej cechy dla całego zbioru 
        sigma = np.zeros((nbfeatures,nbfeatures))
        for f in range(nbfeatures):
            sigma[f,f] = np.var(t[:,f])
        #phi inicjujemy tak, że każda składowa mieszanki ma takie samee prawdopodobieństwo
        phi = 1.0/nbclusters
        print 'INIT:',tmpmu,sigma,phi
        return {'mu': tmpmu,\
                'sigma': sigma,\
                'phi': phi}

def plot_gauss(mu,sigma):
    ''' Funkcja rysująca kontury funkcji gęstości prawdopodobieństwa 
       dwuwymiarowego rozkładu Gaussa'''

    x = np.arange(-6.0, 6.0001, 0.1)
    y = np.arange(-6.0, 6.0001, 0.1)
    X,Y = np.meshgrid(x, y)
    X.shape = 1,len(x)*len(y)
    Y.shape = 1,len(x)*len(y)
    P = np.vstack((X,Y))
    invS = np.linalg.inv(sigma)
    R = P.T-mu
    z = np.zeros(len(R))
    for i in range(len(R)):
        z[i] = np.exp(-0.5*np.dot( R[i,:].T,np.dot(invS,R[i,:])))
        
    z.shape = len(x),len(y)
    py.contourf(x,y,z,alpha = 0.5)
    py.plot(mu[0],mu[1],'o')

Szkielet algorytmu

Poniższy kod to szkielet właściwej funkcji wykonującej optymalizację. Trzeba go uzupełnić implementując równania z wykładu. Proszę uważnie czytać komentarze.

def expectation_maximization(t, nbclusters=2, nbiter=3, normalize=False,\
        epsilon=0.001, monotony=False, datasetinit=True):
    """
    t - zbiór treningowy, 
    Każdy wiersz t jest przykładem (obserwacją), każda kolumna to cecha 
    'nbclusters' ilość klastrów, z których budujemy model mieszany
    'nbiter' ilość iteracji
    'epsilon' kryterium zbieżności
   
     Powtórz kroki E i M aż do spełnienia warunku |E_t - E_{t-1}| < ε
     
    Funkcja zwraca parametry modelu (centra i macerze kowariancji Gaussów i ich wagi \phi) oraz 
    etykiety punktów zbioru treningowego oznaczające do którego z Gaussów w modelowanej mieszance należą.
    """

    nbobs,nbfeatures = t.shape
   
    ### Opcjonalna normalizacja
    if normalize:
        for f in xrange(nbfeatures):
            t[:,f] /= np.std(t[:,f])


    result = {}
    random.seed()

    # szykujemy tablice na prawdopodobieństwa warunowe
    Pz = np.zeros((nbobs,nbclusters)) # P(z|x): opisywane równaniami (2) i (3) z wykładu 
    Px = np.zeros((nbobs,nbclusters)) # P(x|z): opisywane równaniem (4)  
    
    # inicjujemy parametry dla każdego składnika mieszankni
    # params będzie listą taką, że params[i] to słownik
    # zawierający parametry i-tego składnika mieszanki
    params = []
    for i in xrange(nbclusters):
        params.append( draw_params(t,nbclusters) )

    old_log_estimate = sys.maxint                   # init
    log_estimate = sys.maxint/2 + epsilon      # init
    estimation_round = 0    

    # powtarzaj aż zbiegniesz 
    while (abs(log_estimate - old_log_estimate) > epsilon\
                and (not monotony or log_estimate < old_log_estimate)):
        restart = False
        old_log_estimate = log_estimate   
        ########################################################
        # krok E: oblicz Pz dla każdego przykładu (czyli w oznaczeniach z wykładu w_i^j)
        ########################################################
        # obliczamy prawdopodobieństwa  Px[j,i] = P(x_j|z_j=i)  
        for j in xrange(nbobs): # iterujemy po przykładach
            for i in xrange(nbclusters): # iterujemy po składnikach
                Px[j,i] = pnorm(t[j,:], params[i]['mu'], params[i]['sigma']) #  (równanie 4)

        #  obliczamy prawdopodobieństwa Pz[j,i] = P(z_j=i|x_j)   
        #  najpierw licznik równania (3)   
        for j in xrange(nbobs): 
            for i in xrange(nbclusters):
                Pz[j,i] = .............*params[i]['phi']
        #  mianownik równania (3)
        for j in xrange(nbobs): 
            tmpSum = 0.0
            for i in xrange(nbclusters):
                tmpSum += ..................
        # składamy w całość Pz[j,i] = P(z_j=i|x_j)
            Pz[j,:] /= tmpSum
        
        ###########################################################
        # krok M: uaktualnij paramertry (sets {mu, sigma, phi}) #
        ###########################################################
        #print "iter:", iteration, " estimation#:", estimation_round,\
        #            " params:", params
        for i in xrange(nbclusters):
            print "------------------"
            # parametr phi: równanie (6)
            Sum_w = np.sum(Pz[:,i])
            params[i]['phi'] = Sum_w/nbobs
            if params[i]['phi'] <= 1.0/nbobs:           # restartujemy jeśli zanika nam któraś składowa mieszanki
                restart = True                          
                print "Restarting, p:",params[i]['phi'] 
                break
            print 'i: ',i,' phi: ', params[i]['phi']
            # średnia: równanie (7)
            m = np.zeros(nbfeatures)
            for j in xrange(nbobs):
                m += ......................
            params[i]['mu'] = m/Sum_w
            print 'i: ',i,' mu: ', params[i]['mu']
            
            # macierz kowariancji: równanie (8)
            s = np.matrix(np.zeros((nbfeatures,nbfeatures)))
            for j in xrange(nbobs):
                roznica = np.matrix(t[j,:]-params[i]['mu'])
                s += Pz[j,i]*(roznica.T*roznica)
            params[i]['sigma'] = s/Sum_w
            
            print params[i]['sigma']
            
            ### Testujemy czy składniki się nie sklejają i w razie potrzeby restartujemy
            if not restart:
                restart = True
                for i in xrange(1,nbclusters):
                    if not np.allclose(params[i]['mu'], params[i-1]['mu'])\
                    or not np.allclose(params[i]['sigma'], params[i-1]['sigma']):
                        restart = False
                        break
            if restart:                
                old_log_estimate = sys.maxint                 # init
                log_estimate = sys.maxint/2 + epsilon    # init
                params = [draw_params(t,nbclusters) for i in xrange(nbclusters)] # losujemy nowe parametry startowe
                print 'RESTART'
                continue
            
            
            ####################################
            # liczymy estymatę log wiarygodności: równaie (1)  #
            ####################################
            log_estimate = np.sum([np.log(np.sum(\
                    [Px[j,i]*params[i]['phi'] for i in xrange(nbclusters)]))\
                    for j in xrange(nbobs)])
            print "(EM) poprzednia i aktualna estymata log wiarygodności: ",\
                    old_log_estimate, log_estimate
            estimation_round += 1
        ##########################
        #  rysujemy aktualny stan modelu
        ##########################
        py.ioff()
        py.clf()
        py.ion()
        for i in xrange(nbclusters):
            plot_gauss(np.array(params[i]['mu']),np.array(params[i]['sigma']))
        py.plot(x[:,0],x[:,1],'g.')
        py.axis('equal')
        py.draw()
 
        
        # Pakujemy wyniki
            result['quality'] = -log_estimate
            result['params'] = copy.deepcopy(params)
            result['clusters'] = [[o for o in xrange(nbobs)\
                    if Px[o,c] == max(Px[o,:])]\
                    for c in xrange(nbclusters)]
    return result

Program

Przykładowy program korzystający z powyższych funkcji:

##########################################
#   PROGRAM
#########################################


# robimy mieszankę dwóch gaussów:
#parametry rozkładu
# wektor średnich:
mu1 = [-2,-3] 
# macierz kowariancji:
Sigma1 = np.array([[1, 0.5],
                  [0.5, 1]])
# generujemy dane: 
x1 = np.random.multivariate_normal(mu1, Sigma1, 150) #
mu2 = [-0.5,2] 
# macierz kowariancji:
Sigma2 = np.array([[3, 0.5],
                  [0.5, 1]])
# generujemy dane: 
x2 = np.random.multivariate_normal(mu2, Sigma2, 150) #
# łączymy x1 i x2 aby otrzymac jeden zbiór
x = np.vstack((x1,x2))
py.plot(x[:,0],x[:,1],'g.')
py.axis('equal')
py.show()
py.figure()
res = expectation_maximization(x, nbclusters=2, nbiter=3, normalize=False,\
        epsilon=0.001, monotony=False, datasetinit=True)
py.ioff()
py.show()
# wypisz parametry
print 'Dopasowany model: '
print res['params']

Aby obliczyć gęstość prawdopodobieństwa rozkładu mieszanego dla pewnego nowego punktu "x" możemy zastosować poniższą funkcję:

def prob_mix(params, x):
    '''params - parametry dopasowanego gaussowskiego modelu mieszanego
    x - punkt wejścowy,
    
    funkcja zwraca gestość prawdopodobieństwa, dla x w rozkładzie mieszanym
    '''
    prob = 0
    for i in range(len(params)):
        prob+= pnorm(x, params[i]['mu'], params[i]['sigma']) * params[i]['phi']
    
    
    return prob
#---------------- przykładowe użycie: ----------------
x=(6,-4)
print 'P(x=(',str(x),')):', prob_mix(res['params'], x)