
WnioskowanieStatystyczne/CLT
Centralne Twierdzenie Graniczne
Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na Centralne Twierdzenie Graniczne , według którego rozkład sumy dużej liczby zmiennych losowych o podobnych wielkościach [1] dąży (przy liczbie sumowanych zmiennych dążących do nieskończoności) do rozkładu Gaussa. Poniżej przytoczymy dowód tego twierdzenia dla uproszczonego przypadku sumy zmiennych pochodzących z tego samego rozkładu.[2]
Twierdzenie Lindeberga — Levy'ego
Zakładamy, że [math]x_{i}[/math] są niezależnymi zmiennymi podlegającymi (dowolnemu) rozkładowi o skończonej wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma ^{2}[/math]. Dla [math]n\rightarrow \infty[/math], wielkość
podlega rozkładowi normalnemu o wartości średniej 0 i wariancji 1.
Dowód
W dowodzie skorzystamy z pojęcia funkcji charakterystycznej rozkładu.[3] Określamy ją jako
gdzie [math]i=\sqrt{-1}[/math]. Użyteczne będą następujące związki, które wyprowadzić można bezpośrednio z powyższej definicji:
(różniczkujemy po [math]dt[/math], więc przy każdym różniczkowaniu spada nam z wykładnika [math]i x[/math], [math]x[/math] zostaje pod całką a [math]i[/math] jako stała wychodzi przed całkę)
n-ta pochodna funkcji tworzącej w zerze, czyli dla [math]t=0[/math], będzie wynosić
Kolejny użyteczny fakt zachodzi dla niezależnych zmiennych [math]x[/math] i [math]y[/math]:
Funkcja tworząca rozkładu normalnego o wartości oczekiwanej 0 i jednostkowej wariancji będzie miała postać
W analizie sygnałów wynik ten będzie oznaczał, że tranformata Fouriera funkcji Gaussa jest również funkcją Gaussa. Do wyliczeń zastąpionych powyżej przez (...) możemy np. skorzystać z tablicy całek oznaczonych, w których znajdujemy wzór [math]\int\limits_{-\infty}^\infty e^{-a x^2 + 2 b x} dx = \sqrt{\frac{\pi}{a}} e^{-\frac{b^2}{a}}[/math] dla [math]a\gt 0[/math].
Wróćmy do dowodu --- interesuje nas suma zmiennych [math]x_i[/math] o wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma^2[/math]. Funkcję tworzącą dla jednej zmiennej [math]x_i[/math] możemy rozwinąć w szereg Taylora
wokół [math]z_0[/math]. Rozpatrzmy zmienną [math]y_i[/math] przesuniętą względem [math]x_i[/math] o [math]-\mu[/math] i przeskalowaną czynnikiem [math]\sigma\sqrt{n}[/math]:
Wtedy z (3) wynika, że [math]\phi^{(0)}(0)=1[/math], [math]\phi^{(1)}(0)=0[/math], a [math]\phi^{(2)}(0)=-\frac1 n[/math], czyli funkcja tworząca [math]y_i[/math] rozwinięta w szereg Taylora (5) będzie miała postać
Korzystając ze wzoru (4) możemy przedstawić pierwsze wyrazy rozwinięcia Taylora sumy [math]y=\sum_{i=1}^n y_i[/math], odpowiadającej transformacji (1) z dowodzonego twierdzenia, jako iloczyn [math]n[/math] funkcji tworzących (6):
[math] \phi_y(t)=\left(1-\frac{t^2}{2n}+\ldots\right)^n. [/math]
Przy przejściu z [math]n[/math] do nieskończoności (i konsekwentnym pomijaniu wyrazów rzędu [math]n^{-2}[/math]) dostajemy
czyli funkcję tworzącą rozkładu normalnego.
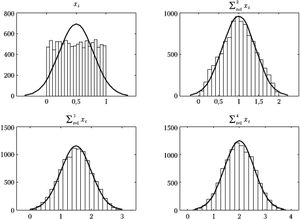
Rysunek 1 ilustruje powyższe twierdzenie dla przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do normalnego. Niestety, często istotne bywają różnice w ,,ogonach, czyli dla wartości bardzo dużych lub bardzo małych. Otóż według wzoru wartości gęstości prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie nie osiągają. Inaczej mówiąc, prawdopodobieństwo wylosowania dowolnie dużej wartości z rozkładu Gaussa będzie małe, ale nie zerowe. Za to suma np. czterech zmiennych z rozkładu równomiernego od zera do jedynki (prawy dolny wykres rys. 1) nie przekroczy nigdy wartości 4, czyli prawdopodobieństwo dla [math]x\gt 4[/math] będzie dokładnie zerem. I choć w skali rysunku 1 efekt ten jest prawie niewidoczny, warto pamiętać, że testy oparte na założeniu normalności rozkładów często operują właśnie w okolicach tych "ogonów", gdzie przybliżenie rozkładu normalnego, uzyskane za pomocą tej prostej procedury, zawodzi.
- ↑ Chodzi o to, aby żadna ze zmiennych w tej sumie nie dominowała nad innymi.
- ↑ Dokładniejsze sformułowania Twierdzenia można znaleźć w książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich.
- ↑ W innych dziedzinach funkcja ta występuje pod nazwą transformaty Fouriera.