WnioskowanieStatystyczne/Test chi2: Różnice pomiędzy wersjami
| (Nie pokazano 6 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 8: | Linia 8: | ||
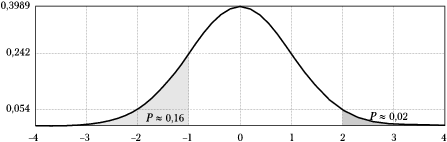
| − | [[Plik:Rozklad_gaussa.png|600px|thumb| | + | [[Plik:Rozklad_gaussa.png|600px|thumb|center|<math>N(0,1)</math>, czyli |
standardowy rozkład Gaussa o zerowej średniej (<math>\mu=0</math>) i | standardowy rozkład Gaussa o zerowej średniej (<math>\mu=0</math>) i | ||
jednostkowej wariancji (<math>\sigma=1</math>).]] | jednostkowej wariancji (<math>\sigma=1</math>).]] | ||
| + | |||
Rozważmy sumę kwadratów zmiennych z rozkładu Gaussa. | Rozważmy sumę kwadratów zmiennych z rozkładu Gaussa. | ||
| Linia 16: | Linia 17: | ||
z rozkładu normalnego o zerowej średniej <math>\mu=0</math> i jednostkowej | z rozkładu normalnego o zerowej średniej <math>\mu=0</math> i jednostkowej | ||
wariancji <math>\sigma ^{2}=1.</math> Suma | wariancji <math>\sigma ^{2}=1.</math> Suma | ||
| + | |||
| + | <center> | ||
<equation id="eq:111"> | <equation id="eq:111"> | ||
<math> | <math> | ||
| + | \displaystyle | ||
\chi ^2=\sum\limits_{i=1}^N x_i^2 | \chi ^2=\sum\limits_{i=1}^N x_i^2 | ||
</math> | </math> | ||
</equation> | </equation> | ||
| + | </center> | ||
| + | |||
będzie podlegać<ref>Dowód tego faktu można znaleźć np. w [http://www.wnt.com.pl/product.php?action=0&prod_id=1488&hot=1 książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich].</ref> rozkładowi <math>\chi^2</math> o gęstości prawdopodobieństwa danej następującym równaniem: | będzie podlegać<ref>Dowód tego faktu można znaleźć np. w [http://www.wnt.com.pl/product.php?action=0&prod_id=1488&hot=1 książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich].</ref> rozkładowi <math>\chi^2</math> o gęstości prawdopodobieństwa danej następującym równaniem: | ||
| + | |||
| + | |||
| + | <center> | ||
<equation id="eq:112"> | <equation id="eq:112"> | ||
<math> | <math> | ||
| + | \displaystyle | ||
p(\chi ^{2})=\frac{1}{\Gamma \left(\frac{f}{2}\right)2^{\frac{f}{2}}} | p(\chi ^{2})=\frac{1}{\Gamma \left(\frac{f}{2}\right)2^{\frac{f}{2}}} | ||
\left(\chi^{2}\right)^{\frac{f}{2}-1}e^{-\frac{\chi ^{2}}{2}} , | \left(\chi^{2}\right)^{\frac{f}{2}-1}e^{-\frac{\chi ^{2}}{2}} , | ||
</math> | </math> | ||
</equation> | </equation> | ||
| + | </center> | ||
| + | |||
gdzie <math>f</math> oznacza liczbę stopni swobody, | gdzie <math>f</math> oznacza liczbę stopni swobody, | ||
a <math>\Gamma</math> funkcję Eulera.<ref> | a <math>\Gamma</math> funkcję Eulera.<ref> | ||
| Linia 34: | Linia 46: | ||
</ref> | </ref> | ||
| − | W przypadku, gdy zmienne w | + | W przypadku, gdy zmienne w <xr id="eq:111">sumie </xr> są |
niezależne, <math>f=N</math>, czyli liczba stopni swobody jest równa | niezależne, <math>f=N</math>, czyli liczba stopni swobody jest równa | ||
liczbie składników w sumie <xr id="eq:111">(%i)</xr>. W praktyce, jak | liczbie składników w sumie <xr id="eq:111">(%i)</xr>. W praktyce, jak | ||
| Linia 162: | Linia 174: | ||
wynosi <math>Np_i</math>, gdzie <math>p_i</math> jest całką rozkładu w granicach <math>i</math>-tego | wynosi <math>Np_i</math>, gdzie <math>p_i</math> jest całką rozkładu w granicach <math>i</math>-tego | ||
przedziału histogramu (wartości te reprezentują na górnym wykresie <xr id="fig:119">rys. %i</xr> wąskie szare słupki). Jeśli ilość danych w <math>i</math>-tym binie<ref>W literaturze polskojęzycznej bin określa się również jako "przedział stałych wartości histogramu".</ref> histogramu oznaczymy jako <math>n_i</math>, to wygodną miarą rozbieżności danych od hipotetycznego rozkładu może być suma kwadratów <math>\sum(n_i-Np_i)^2</math>. Wyrazy tej sumy warto podzielić przez wartość oczekiwaną w każdym binie, czyli <math>Np_i</math>, dzięki czemu zaproponowana przez Pearsona w roku 1900 statystyka | przedziału histogramu (wartości te reprezentują na górnym wykresie <xr id="fig:119">rys. %i</xr> wąskie szare słupki). Jeśli ilość danych w <math>i</math>-tym binie<ref>W literaturze polskojęzycznej bin określa się również jako "przedział stałych wartości histogramu".</ref> histogramu oznaczymy jako <math>n_i</math>, to wygodną miarą rozbieżności danych od hipotetycznego rozkładu może być suma kwadratów <math>\sum(n_i-Np_i)^2</math>. Wyrazy tej sumy warto podzielić przez wartość oczekiwaną w każdym binie, czyli <math>Np_i</math>, dzięki czemu zaproponowana przez Pearsona w roku 1900 statystyka | ||
| + | |||
<center> | <center> | ||
<equation id="eq:118"> | <equation id="eq:118"> | ||
<math> | <math> | ||
| + | \displaystyle | ||
\chi ^{2}=\sum\limits_{i=1}^r \frac{\left( n_i-N p_i\right) ^{2}}{N p_i} | \chi ^{2}=\sum\limits_{i=1}^r \frac{\left( n_i-N p_i\right) ^{2}}{N p_i} | ||
</math> | </math> | ||
</equation> | </equation> | ||
</center> | </center> | ||
| + | |||
dla <math>N\rightarrow\infty</math> i odpowiednio dużych | dla <math>N\rightarrow\infty</math> i odpowiednio dużych | ||
| Linia 195: | Linia 210: | ||
zwykle przynajmniej pięć. Dla mniejszych ilości zliczeń w binach, | zwykle przynajmniej pięć. Dla mniejszych ilości zliczeń w binach, | ||
<math>\chi^2</math> nie będzie dobrym przybliżeniem rozkładu powyższej | <math>\chi^2</math> nie będzie dobrym przybliżeniem rozkładu powyższej | ||
| − | statystyki. | + | statystyki — w takich przypadkach możemy zastosować test oparty na dokładnych wartościach statystyki, wyliczanych kombinatorycznie, jak np. dokładny test Fishera; dokładne statystyki można oczywiście stosować w każdym przypadku. |
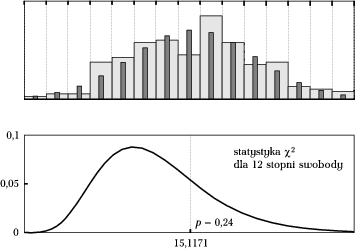
[[Plik:chi2Pearson.png|thumb|center|600px|<figure id="fig:119"></figure>Górny wykres: histogram 200 wartości (jasne, szerokie słupki); wąskie (ciemniejsze) słupki przedstawiają wartości oczekiwane <math>Np_i</math>, gdzie <math>p_i</math> są całkami dopasowanej krzywej (rozkładu Gaussa) w odpowiednim przedziale. Dolny wykres: rozkład statystyki <math>\chi^2=\sum_{i=1}^{15} \frac{(n_i-Np_i)^2}{Np_i}</math> dla 12 stopni swobody (15 binów minus więzy: wyznaczone z danych <math>\mu</math>, <math>\sigma</math> oraz <math>\sum_{i=1}^{15}n_i=N</math>) z zaznaczoną wartością <math>\chi^2_d</math> dla danych z lewego wykresu. Ponieważ <math>\int_{\chi^2_d}^\infty p(\chi^2)=0,24</math>, hipotezę o pochodzeniu danych z rozkładu normalnego możemy przyjąć na poziomie istotności nawet 48% (test dwustronny).]] | [[Plik:chi2Pearson.png|thumb|center|600px|<figure id="fig:119"></figure>Górny wykres: histogram 200 wartości (jasne, szerokie słupki); wąskie (ciemniejsze) słupki przedstawiają wartości oczekiwane <math>Np_i</math>, gdzie <math>p_i</math> są całkami dopasowanej krzywej (rozkładu Gaussa) w odpowiednim przedziale. Dolny wykres: rozkład statystyki <math>\chi^2=\sum_{i=1}^{15} \frac{(n_i-Np_i)^2}{Np_i}</math> dla 12 stopni swobody (15 binów minus więzy: wyznaczone z danych <math>\mu</math>, <math>\sigma</math> oraz <math>\sum_{i=1}^{15}n_i=N</math>) z zaznaczoną wartością <math>\chi^2_d</math> dla danych z lewego wykresu. Ponieważ <math>\int_{\chi^2_d}^\infty p(\chi^2)=0,24</math>, hipotezę o pochodzeniu danych z rozkładu normalnego możemy przyjąć na poziomie istotności nawet 48% (test dwustronny).]] | ||
| Linia 209: | Linia 224: | ||
====Przykład==== | ====Przykład==== | ||
| + | <center> | ||
<figure id="fig:120"> | <figure id="fig:120"> | ||
{|class="wikitable" | {|class="wikitable" | ||
| Linia 239: | Linia 255: | ||
|} | |} | ||
<caption>Powyższa tabela sumuje liczby ofiar słynnej katastrofy statku pasażerskiego Titanic (zob. [http://www.encyclopedia-titanica.org http://www.encyclopedia-titanica.org]) w zależności od klasy, którą podróżowali pasażerowie. Czy wykupienie biletu w pierwszej zamiast trzeciej klasie zwiększało szanse przeżycia?</caption></figure> | <caption>Powyższa tabela sumuje liczby ofiar słynnej katastrofy statku pasażerskiego Titanic (zob. [http://www.encyclopedia-titanica.org http://www.encyclopedia-titanica.org]) w zależności od klasy, którą podróżowali pasażerowie. Czy wykupienie biletu w pierwszej zamiast trzeciej klasie zwiększało szanse przeżycia?</caption></figure> | ||
| + | </center> | ||
Okazuje się, że wśród uratowanych było więcej pasażerów III klasy (178), | Okazuje się, że wśród uratowanych było więcej pasażerów III klasy (178), | ||
| Linia 249: | Linia 266: | ||
wszystkich pasażerów niezależnie od klasy i ocenić je można jako stosunek | wszystkich pasażerów niezależnie od klasy i ocenić je można jako stosunek | ||
ilości uratowanych (499) do wszystkich pasażerów (1316), czyli ok. 38%<ref>dokładnie 37,9..., w tekście przytaczamy wartości bardziej zaokrąglone niż w faktycznych obliczeniach.</ref> W tej sytuacji spośród pasażerów III klasy powinno ocaleć 38% z 706, czyli prawie prawie 268<ref>Dokładniej 267,5. Nie oznacza to bynajmniej, że jeden pasażer | ilości uratowanych (499) do wszystkich pasażerów (1316), czyli ok. 38%<ref>dokładnie 37,9..., w tekście przytaczamy wartości bardziej zaokrąglone niż w faktycznych obliczeniach.</ref> W tej sytuacji spośród pasażerów III klasy powinno ocaleć 38% z 706, czyli prawie prawie 268<ref>Dokładniej 267,5. Nie oznacza to bynajmniej, że jeden pasażer | ||
| − | powinien ocaleć | + | powinien ocaleć "połowicznie", tylko że 267 i 268 są liczbami najbliższymi |
najbardziej prawdopodobnej.</ref>, z drugiej klasy 38% z 285 czyli około 108, wreszcie z pierwszej klasy — 38% z 325, czyli około123 pasażerów. | najbardziej prawdopodobnej.</ref>, z drugiej klasy 38% z 285 czyli około 108, wreszcie z pierwszej klasy — 38% z 325, czyli około123 pasażerów. | ||
Przewidywane ilości zaginionych możemy obliczyć z analogicznych proporcji — w każdej klasie powinno zginąć średnio 817/1316 czyli ok. 62% pasażerów. W ten sposób możemy stworzyć tabelę: | Przewidywane ilości zaginionych możemy obliczyć z analogicznych proporcji — w każdej klasie powinno zginąć średnio 817/1316 czyli ok. 62% pasażerów. W ten sposób możemy stworzyć tabelę: | ||
| + | |||
| + | <center> | ||
<figure id="fig:121"> | <figure id="fig:121"> | ||
{|class="wikitable" | {|class="wikitable" | ||
| Linia 283: | Linia 302: | ||
|} | |} | ||
<caption>Wartości oczekiwane dla tabeli z tabeli <xr id="fig:120"> %i</xr> (zaokrąglone do liczb całkowitych) w świetle hipotezy o niezależności kolumn i wierszy.</caption></figure> | <caption>Wartości oczekiwane dla tabeli z tabeli <xr id="fig:120"> %i</xr> (zaokrąglone do liczb całkowitych) w świetle hipotezy o niezależności kolumn i wierszy.</caption></figure> | ||
| + | </center> | ||
| + | |||
Zwróćmy uwagę, że obliczone w ten sposób wartości oczekiwane dają takie same | Zwróćmy uwagę, że obliczone w ten sposób wartości oczekiwane dają takie same | ||
| Linia 288: | Linia 309: | ||
W ogólnym przypadku dla tabeli o wymiarach <math>3\times 2</math>: | W ogólnym przypadku dla tabeli o wymiarach <math>3\times 2</math>: | ||
| + | <center> | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Linia 298: | Linia 320: | ||
|f | |f | ||
|} | |} | ||
| + | </center> | ||
i wartości brzegowych: | i wartości brzegowych: | ||
| + | <center> | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Linia 318: | Linia 342: | ||
|(a+b+c+d+e+f) | |(a+b+c+d+e+f) | ||
|} | |} | ||
| + | </center> | ||
| − | + | ||
| − | oczekiwane przedstawione w | + | Hipotezę o niezależności kolumn i wierszy wyrażać będą wartości |
| + | oczekiwane przedstawione w <xr id="fig:122">tabeli</xr>. | ||
| + | |||
| + | |||
| + | <center> | ||
<figure id="fig:122"> | <figure id="fig:122"> | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | |<math>\frac{(a+b+c)(a+d)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(a+b+c)(a+d)}{a+b+c+d+e+f}</math> |
| − | |<math>\frac{(a+b+c)(b+e)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(a+b+c)(b+e)}{a+b+c+d+e+f}</math> |
| − | |<math>\frac{(a+b+c)(c+f)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(a+b+c)(c+f)}{a+b+c+d+e+f}</math> |
| − | |(a+b+c) | + | |<math>(a+b+c)</math> |
|- | |- | ||
| − | |<math>\frac{(d+e+f)(a+d)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(d+e+f)(a+d)}{a+b+c+d+e+f}</math> |
| − | |<math>\frac{(d+e+f)(b+e)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(d+e+f)(b+e)}{a+b+c+d+e+f}</math> |
| − | |<math>\frac{(d+e+f)(c+f)}{a+b+c+d+e+f}</math> | + | |<math>\displaystyle\frac{(d+e+f)(c+f)}{a+b+c+d+e+f}</math> |
| − | |(d+e+f) | + | |<math>(d+e+f)</math> |
|- | |- | ||
| − | |(a+d) | + | |<math>(a+d)</math> |
| − | |(b+e) | + | |<math>(b+e)</math> |
| − | |(c+f) | + | |<math>(c+f)</math> |
| − | |(a+b+c+d+e+f) | + | |<math>(a+b+c+d+e+f)</math> |
|} | |} | ||
<caption>Wartości oczekiwane dla hipotezy o niezależności kolumn i wierszy tabeli <math>3\times 2</math>.</caption></figure> | <caption>Wartości oczekiwane dla hipotezy o niezależności kolumn i wierszy tabeli <math>3\times 2</math>.</caption></figure> | ||
| + | </center> | ||
| + | |||
| − | Ale wróćmy do pytania postawionego w | + | Ale wróćmy do pytania postawionego w <xr id="fig:120"> |
| − | + | przykładzie</xr>. Porównując dane z tego przykładu z <xr id="fig:121"> | |
| − | + | tabelą</xr> widzimy, że w klasach pierwszej i drugiej ocalało więcej | |
pasażerów, niż wynikałoby to z hipotezy o niezależności szans | pasażerów, niż wynikałoby to z hipotezy o niezależności szans | ||
przeżycia od klasy. Czy są to różnice statystycznie istotne, czy mogą | przeżycia od klasy. Czy są to różnice statystycznie istotne, czy mogą | ||
| Linia 351: | Linia 382: | ||
Statystycznych. Wartości oczekiwane w świetle hipotezy zerowej | Statystycznych. Wartości oczekiwane w świetle hipotezy zerowej | ||
opisuje <xr id="fig:121">tabela</xr>, a za statystykę testową | opisuje <xr id="fig:121">tabela</xr>, a za statystykę testową | ||
| − | posłuży <math>\chi^2</math> Pearsona | + | posłuży <math>\chi^2</math> Pearsona: |
| − | |||
| Linia 358: | Linia 388: | ||
<equation id="eq:123"> | <equation id="eq:123"> | ||
<math> | <math> | ||
| + | \displaystyle | ||
\chi^2=\sum\limits_{i=1}^r | \chi^2=\sum\limits_{i=1}^r | ||
\frac{(n_i^{\textrm{obserwowane}}-n_i^{\textrm{oczekiwane}})^2}{n_i^{\textrm{oczekiwane}}}, | \frac{(n_i^{\textrm{obserwowane}}-n_i^{\textrm{oczekiwane}})^2}{n_i^{\textrm{oczekiwane}}}, | ||
| Linia 383: | Linia 414: | ||
dokładne wartości <math>n_i^{\textrm{oczekiwane}}</math>, które nie muszą wyrażać się liczbami całkowitymi.</ref> | dokładne wartości <math>n_i^{\textrm{oczekiwane}}</math>, które nie muszą wyrażać się liczbami całkowitymi.</ref> | ||
| + | |||
| + | <center> | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Linia 393: | Linia 426: | ||
|<math>\frac{(528-438)^2}{438}</math> | |<math>\frac{(528-438)^2}{438}</math> | ||
|} | |} | ||
| + | </center> | ||
| + | |||
Suma tych wartości wynosi ponad 133. Prawdopodobieństwo przypadkowego | Suma tych wartości wynosi ponad 133. Prawdopodobieństwo przypadkowego | ||
Aktualna wersja na dzień 05:29, 5 kwi 2024
Spis treści
Rozkład [math]\chi ^2[/math]
Próbując doprowadzić problem z poprzedniego rozdziału do rozkładu normalnego, doszliśmy do rozkładu Studenta. W tym rozdziale postąpimy odwrotnie: najpierw wprowadzimy nowy rozkład prawdopodobieństwa, a potem znajdziemy dla niego ciekawe zastosowania.
Rozważmy sumę kwadratów zmiennych z rozkładu Gaussa.
Oznaczmy jako [math]\left\{x_i\right\}[/math] niezależne zmienne losowe
z rozkładu normalnego o zerowej średniej [math]\mu=0[/math] i jednostkowej
wariancji [math]\sigma ^{2}=1.[/math] Suma
będzie podlegać[1] rozkładowi [math]\chi^2[/math] o gęstości prawdopodobieństwa danej następującym równaniem:
gdzie [math]f[/math] oznacza liczbę stopni swobody, a [math]\Gamma[/math] funkcję Eulera.[2]
W przypadku, gdy zmienne w sumie 1 są niezależne, [math]f=N[/math], czyli liczba stopni swobody jest równa liczbie składników w sumie (1). W praktyce, jak zobaczymy w poniższych przykładach, do statystyki [math]\chi^2[/math] dochodzimy zwykle estymując potrzebne parametry z próby. Wtedy liczba stopni swobody jest równa liczbie elementów próby pomniejszonej o ilość więzów, czyli estymowanych z niej parametrów, wykorzystanych do obliczenia statystyki (1).
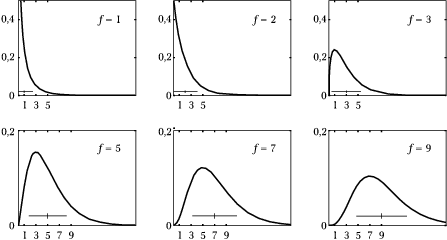
Wartość oczekiwana rozkładu [math]\chi^2[/math] jest równa liczbie stopni swobody [math]f[/math], a wariancja jest równa [math]2f[/math]. Również kształt rozkładu zależy od [math]f[/math]: poniższy rysunek 1 przedstawia wykresy [math]p(\chi^2)[/math] dla kilku wartości [math]f[/math].
Za dokładnie?
Wróćmy raz jeszcze do przykładu z rozdziału Weryfikacja hipotez statystycznych. Tym razem skoncentrujemy się na rozrzucie wyników:
Studenci wykonują ćwiczenie za pomocą znanego układu doświadczalnego, dla którego prawidłowo przeprowadzane pomiary dają wyniki z rozkładu normalnego o odchyleniu standardowym 0,1. Jakie jest prawdopodobieństwo, że seria wyników: 9,78, 9,81, 9,83, 9,86 i 9,79 pochodzi z pomiarów przeprowadzanych na tym zestawie?
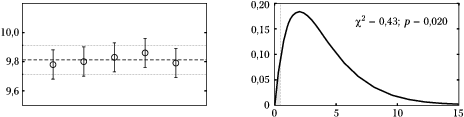
Przyjrzyjmy się tym danym w kontekście znanej wariancji. Lewy wykres na rysunku 2 przedstawia te liczby oraz ich średnią (linia przerywana) z zaznaczonym przedziałem [math]\pm[/math] odchylenie standardowe. Przedział ten bywa zwany potocznie "korytarzem błędu", tak jak odchylenie standardowe bywa czasami nazywane "błędem". Czy słusznie?
Jeśli interpretować odchylenie standardowe jako "błąd", wszystko wydaje się w najlepszym porządku: wszystkie pomiary leżą "w granicach błędu". Ale czym tak naprawdę jest odchylenie standardowe? Definicja wariancji dana wzorem w rozdziale o momentach nie wyjaśnia dokładnie, jaka część zmiennych powinna się znaleźć w odległości mniejszej niż jej pierwiastek (czyli odchylenie standardowe) od wartości oczekiwanej.[3] Jednak w przypadku, gdy znamy (lub co najmniej zakładamy) postać rozkładu, możemy już te wielkości dokładnie obliczyć. Z zależności podanej w rozdziale o rozkładzie Gaussa wynika, że średnio ok. 36% przypadków losowanych z rozkładu Gaussa przyjmuje wartości oddalone o więcej niż jedno odchylenie standardowe od wartości średniej. A tu wszystkie pięć wypada bliżej... Trochę podejrzane, ale to jeszcze nie dowód, gdyż 36% powinniśmy otrzymać jako średnią wartość dopiero w odpowiednio długiej serii. Spróbujmy więc poszukać innej miary wiarygodności dla tego przypadku.
Skoro mamy się koncentrować na wariancji, usuńmy z hipotezy
wartość oczekiwaną — rozrzut lepiej liczyć względem wartości
średniej próby.
Można udowodnić, [4]
że wielkość
gdzie [math]\overline{x}=\frac 1 N \sum\limits_{i=1}^N x_i [/math], podlega rozkładowi [math]\chi^2[/math] o [math]N-1[/math] stopniach swobody.
Rozkład ten przedstawiony jest w prawej części rysunku 2. Zaznaczono na nim również (przerywaną linią pionową) wartość statystyki [math]\chi^2[/math], obliczoną dla dyskutowanego przypadku. Okazuje się, że wartość ta jest podejrzanie mała! Prawdopodobieństwo uzyskania tak niewielkiej (lub jeszcze mniejszej) wartości [math]\chi^2[/math] nie przekracza 2%, więc nawet test dwustronny na poziomie istotności 5% odrzuciłby hipotezę mówiącą, że zmienne pochodzą z rozkładu normalnego o odchyleniu standardowym równym 0,1!
Można to zjawisko uznać za model "naciągania" wyników — czujemy się lepiej, gdy przedstawiamy wyniki bliskie wartości uznawanej za prawidłową. Oczywiście jest to nieuczciwa praktyka, którą — jak widać — można wykryć, jeżeli dysponujemy informacją o wariancji. Co ciekawe, "wpadki" tego typu zdarzają się nawet w raportach z badań naukowych — w tym przypadku przyczyną bywa raczej (poza niezrozumieniem statystyki) tendencja do ostrożnego zawyżania oceny błędów.
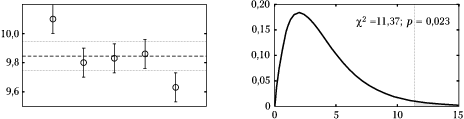
Częściej spotykamy się z sytuacją, w której rozrzut jest "za duży" w stosunku do hipotezy o wariancji, jak na rysunku %i 3. Jeśli odchylenia od wartości średniej będą duże w stosunku do wariancji, otrzymamy dużą wartość statystyki [math]\chi^2[/math]. W świetle rozkładu [math]\chi^2[/math] dla odpowiedniej liczby stopni swobody, taka wartość powinna sugerować odrzucenie hipotezy mówiącej, że zmienne pochodzą z rozkładu normalnego o wariancji [math]\sigma[/math].
Test [math]\chi^2[/math] Pearsona
Zdecydowana większość klasycznych testów opiera się na założeniu, że zmienne pochodzą z populacji o rozkładzie normalnym. Stosując taki test przyjmujemy za to założenie odpowiedzialność — jeśli nie było ono spełnione, wynik testu może okazać się nieprawdziwy.
Ale jak to sprawdzić, jeśli jedyną informacją o populacji jest próba złożona z [math]N[/math] elementów? Dobrym zwyczajem jest oglądanie histogramów analizowanych danych. Na rysunku w rozdziale o Centralnym Twierdzeniu Granicznym używaliśmy histogramów i wykresu dopasowanych do nich funkcji Gaussa jako praktycznych argumentów za Centralnym Twierdzeniem Granicznym. Jak oceniamy "wzrokowo" podobieństwo histogramu do krzywej?
W każdym z przedziałów histogramu porównujemy liczbę przypadków zliczonych z danych (np. na górnym wykresie rys. 4 określają je szerokie jasne słupki) z wykresem dopasowanej funkcji, określającej hipotezę o rozkładzie. Liczba przypadków określona przez hipotezę o rozkładzie wynosi [math]Np_i[/math], gdzie [math]p_i[/math] jest całką rozkładu w granicach [math]i[/math]-tego przedziału histogramu (wartości te reprezentują na górnym wykresie rys. 4 wąskie szare słupki). Jeśli ilość danych w [math]i[/math]-tym binie[5] histogramu oznaczymy jako [math]n_i[/math], to wygodną miarą rozbieżności danych od hipotetycznego rozkładu może być suma kwadratów [math]\sum(n_i-Np_i)^2[/math]. Wyrazy tej sumy warto podzielić przez wartość oczekiwaną w każdym binie, czyli [math]Np_i[/math], dzięki czemu zaproponowana przez Pearsona w roku 1900 statystyka
dla [math]N\rightarrow\infty[/math] i odpowiednio dużych
[math]Np_i[/math] podlega[6] rozkładowi [math]\chi^2[/math]. Za "odpowiednio duże" ilości
przypadków w każdym z przedziałów [math]Np_i[/math] przyjmuje się
zwykle przynajmniej pięć. Dla mniejszych ilości zliczeń w binach,
[math]\chi^2[/math] nie będzie dobrym przybliżeniem rozkładu powyższej
statystyki — w takich przypadkach możemy zastosować test oparty na dokładnych wartościach statystyki, wyliczanych kombinatorycznie, jak np. dokładny test Fishera; dokładne statystyki można oczywiście stosować w każdym przypadku.
Test niezależności kolumn i wierszy w tabelach
Test [math]\chi^2[/math] Pearsona można wykorzystać do analizy tabel, w których, podobnie jak w binach histogramu, znajdują się zliczenia przypadków. Tabele takie zwane są w języku angielskim contingency tables ; słownik Międzynarodowego Instytutu Statystyki[7] podaje jako polskie tłumaczenie "tablica kontyngencyjna" lub "tablica wielodzielcza".
Przykład
| klasa[math]\rightarrow[/math] | I | II | III | razem[math]\downarrow[/math] |
|---|---|---|---|---|
| uratowanych | 203 | 118 | 178 | 499 |
| zaginionych | 122 | 167 | 528 | 817 |
| razem[math]\rightarrow[/math] | 325 | 285 | 706 | 1316 |
Okazuje się, że wśród uratowanych było więcej pasażerów III klasy (178), niż pasażerów II klasy (118). Ale być może wynika to po prostu z faktu, że trzecią klasą podróżowało w ogóle więcej pasażerów (706) niż drugą (285)? Trzeba te proporcje wziąć pod uwagę.
Załóżmy, że szansa przeżycia nie miała nic wspólnego z tym, którą klasą podróżował pasażer. W takim przypadku szanse przeżycia byłyby jednakowe dla wszystkich pasażerów niezależnie od klasy i ocenić je można jako stosunek ilości uratowanych (499) do wszystkich pasażerów (1316), czyli ok. 38%[8] W tej sytuacji spośród pasażerów III klasy powinno ocaleć 38% z 706, czyli prawie prawie 268[9], z drugiej klasy 38% z 285 czyli około 108, wreszcie z pierwszej klasy — 38% z 325, czyli około123 pasażerów. Przewidywane ilości zaginionych możemy obliczyć z analogicznych proporcji — w każdej klasie powinno zginąć średnio 817/1316 czyli ok. 62% pasażerów. W ten sposób możemy stworzyć tabelę:
| klasa[math]\rightarrow[/math] | I | II | III | razem[math]\downarrow[/math] |
|---|---|---|---|---|
| uratowanych | 123 | 108 | 268 | 499 |
| zaginionych | 202 | 177 | 438 | 817 |
| razem[math]\rightarrow[/math] | 325 | 285 | 706 | 1316 |
Zwróćmy uwagę, że obliczone w ten sposób wartości oczekiwane dają takie same
wartości brzegowe (czyli sumy po wierszach i kolumnach) jak dane oryginalne.
W ogólnym przypadku dla tabeli o wymiarach [math]3\times 2[/math]:
| a | b | b |
| d | e | f |
i wartości brzegowych:
| a | b | b | (a+b+c) |
| d | e | f | (d+e+f) |
| (a+d) | (b+e) | (c+f) | (a+b+c+d+e+f) |
Hipotezę o niezależności kolumn i wierszy wyrażać będą wartości
oczekiwane przedstawione w tabeli 7.
| [math]\displaystyle\frac{(a+b+c)(a+d)}{a+b+c+d+e+f}[/math] | [math]\displaystyle\frac{(a+b+c)(b+e)}{a+b+c+d+e+f}[/math] | [math]\displaystyle\frac{(a+b+c)(c+f)}{a+b+c+d+e+f}[/math] | [math](a+b+c)[/math] |
| [math]\displaystyle\frac{(d+e+f)(a+d)}{a+b+c+d+e+f}[/math] | [math]\displaystyle\frac{(d+e+f)(b+e)}{a+b+c+d+e+f}[/math] | [math]\displaystyle\frac{(d+e+f)(c+f)}{a+b+c+d+e+f}[/math] | [math](d+e+f)[/math] |
| [math](a+d)[/math] | [math](b+e)[/math] | [math](c+f)[/math] | [math](a+b+c+d+e+f)[/math] |
Ale wróćmy do pytania postawionego w przykładzie 5. Porównując dane z tego przykładu z tabelą 6 widzimy, że w klasach pierwszej i drugiej ocalało więcej
pasażerów, niż wynikałoby to z hipotezy o niezależności szans
przeżycia od klasy. Czy są to różnice statystycznie istotne, czy mogą
wynikać z przypadku?
Trzeba oczywiście wrócić do Schematu Weryfikacji Hipotez Statystycznych. Wartości oczekiwane w świetle hipotezy zerowej opisuje tabela 6, a za statystykę testową posłuży [math]\chi^2[/math] Pearsona:
gdzie [math]n_i^{\textrm{obserwowane}}[/math] pochodzić będą
bezpośrednio z tabeli 5, a
[math]n_i^{\textrm{oczekiwane}}[/math] z tabeli 6. Liczba stopni swobody dla testu tabeli o wymiarach
[math]3\times 2[/math] wynosi [math](3-1)(2-1)=2[/math]. W ogólnym
przypadku dla tabeli o wymiarach [math]n\times m[/math] ilość stopni
swobody dla testu [math]\chi^2[/math] wynosi[10] [math](n-1)(m-1)[/math].
Według wzoru (5) sumować będziemy następujące wartości:[11]
| [math]\frac{(203-123)^2}{123}[/math] | [math]\frac{(118-108)^2}{108}[/math] | [math]\frac{(178-268)^2}{268}[/math] |
| [math]\frac{(122-202)^2}{202}[/math] | [math]\frac{(167-177)^2}{177}[/math] | [math]\frac{(528-438)^2}{438}[/math] |
Suma tych wartości wynosi ponad 133. Prawdopodobieństwo przypadkowego
uzyskania tak wielkiego [math]\chi^2[/math] dla dwóch stopni swobody
jest bardzo bliskie zera, więc zależność szans na przeżycie w tej
katastrofie od tego, którą klasą podróżował pasażer, możemy uznać za
istotną.
- ↑ Dowód tego faktu można znaleźć np. w książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich.
- ↑ [math]\Gamma(x+1)=\int_0^\infty t^xe^{-t}dt[/math]; [math]\Gamma(n+1)=n![/math] dla [math]n=1,2,\ldots[/math]
- ↑ Oszacowanie w ogólnym przypadku podaje nierówność Czebyszewa: [math] P(\left| X-\overline{x}\right| \gt k\sigma )\lt k^{-2},\ \ k\in \mathbb{R}^{+}. [/math] Dowód: [math] \sigma ^{2}=\underset{-\infty }{\overset{\infty }{\int }}(x- \overline{x})^{2}p(x)dx\geq \underset{\left| x-\overline{x}\right| \geq k\sigma }\int (x-\overline{x})^{2}p(x)dx\geq k^{2}\sigma ^{2}\underset{ \left| x-\overline{x}\right| \geq k\sigma }{\int }p(x)dx=k^{2}\sigma ^{2}p(\left| X-\overline{x}\right| \gt k\sigma) [/math] jednak dla jednego odchylenia standardowego nierówność ta nie niesie żadnej informacji.
- ↑ Dowód można znaleźć np. w książce Siegmunda Brandta "Analiza danych. Metody statystyczne i obliczeniowe".
- ↑ W literaturze polskojęzycznej bin określa się również jako "przedział stałych wartości histogramu".
- ↑ Dowód tego faktu można znaleźć np. w książce Romana Nowaka "Statystyka dla Fizyków". Argumentacją (nie zastępującą dowodu) będzie spostrzeżenie, że znajdujące się w mianowniku [math]Np_i[/math] jest równe wartości oczekiwanej rozkładu Poissona dla prawdopodobieństwa [math]p_i[/math]. Ze wzoru w rozdziale o rozkładzie Poissona wynika, że wariancja tego rozkładu wynosi [math]Np_i[/math], więc podstawiając [math]\sigma_{n_i}=\sqrt{Np_i}[/math] wzór %i 4 można wyrazić w postaci: [math] \sum\limits_{i=1}^r \frac{\left( n_i-N p_i\right)^{2}}{N p_i} = \sum\limits_{i=1}^r \frac{\left( n_i-\mu_{n_i}\right) ^{2}}{\sigma_{n_i}}. [/math] Przekształcenie [math]x\rightarrow \frac{x-\mu}{\sigma}[/math] daje zmienne z rozkładu o zerowej średniej i jednostkowej wariancji; udowodnienie, że jest to rozkład Gaussa, wymaga zastosowania przybliżeń, uzasadnionych dla "odpowiednio dużych" [math]Np_i[/math].
- ↑ International Statistical Institute (ISI), http://www.cbs.nl/isi.
- ↑ dokładnie 37,9..., w tekście przytaczamy wartości bardziej zaokrąglone niż w faktycznych obliczeniach.
- ↑ Dokładniej 267,5. Nie oznacza to bynajmniej, że jeden pasażer powinien ocaleć "połowicznie", tylko że 267 i 268 są liczbami najbliższymi najbardziej prawdopodobnej.
- ↑ Zgodnie z przypisem z rozdziału o rozkładzie [math]t[/math] Studenta będzie to liczba niezależnych zmiennych pomniejszona o liczbę obliczonych z nich parametrów — w tym wypadku sumy wierszy i kolumn (z pominięciem całkowitej sumy, którą można z nich obliczyć).
- ↑ W poniższej tabeli zamieszczono wartości oczekiwane zaokrąglone do liczb całkowitych; w obliczeniach wykorzystujemy dokładne wartości [math]n_i^{\textrm{oczekiwane}}[/math], które nie muszą wyrażać się liczbami całkowitymi.