FizykaI FMiN/Grawitacja: Różnice pomiędzy wersjami
(Utworzono nową stronę " <span style="font-size:40px">Grawitacja</span><br><br> ==Prawo powszechnego ciążenia== Prawo powszechnego ciążenia <span style="color:red">Newtona</span> <span s...") |
|||
| Linia 1: | Linia 1: | ||
| − | + | __NOTOC__ | |
<span style="font-size:40px">Grawitacja</span><br><br> | <span style="font-size:40px">Grawitacja</span><br><br> | ||
Aktualna wersja na dzień 09:51, 24 cze 2015
Grawitacja
Prawo powszechnego ciążenia
Prawo powszechnego ciążenia Newtona (1687) mówi, że siła przyciągania grawitacyjnego między dwoma ciałami jest proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości:
| [math] F \; = \; G \; \frac {m\; M}{r^2} [/math] |
Prawo to opisuje zarówno spadanie jabłka z drzewa jak i ruchy Księżyca i planet. Grawitacja jest opisywana przez jeden parametr, stałą Newtona:
- [math]G \approx 6.67 \cdot 10^{-11} \; \frac{N m^2}{kg^2} [/math]
W warunkach laboratoryjnych potwierdzona przez doświadczenie Cavendisha (1798), w którym zmierzył oddziaływanie kul ołowianych masach [math]m=0.73\;kg[/math] i [math]M=158\; kg[/math].
Prawo powszechnego ciążenia sformułowane zostało dla mas punktowych. Ale stosuje się także dla ddziaływań ciał sferycznie symetrycznych
[math] F \; = \; G \; \frac {m\; M}{r^2} [/math]
Siła ciążenia dla ciała o masie [math]m[/math] przy powierzchni Ziemi:
- [math] F \; = \; G \; \frac {m\; M_Z}{R_Z^2} \; \equiv \; g \cdot m [/math]
- [math] \Rightarrow \;\; g \; = \; \frac {G\; M_Z}{R_Z^2}[/math]
Pole grawitacyjne przy powierzchni Ziemi możemy traktować jako jednorodne tylko wtedy, gdy rozważamy ruch na odległościach znacznie mniejszych od promienia Ziemi!
Ruch satelity
Przyjmijmy, że satelita porusza się po orbicie kołowej o promieniu [math]R[/math]. Siła grawitacji
- [math] F \; = \; G \; \frac {m\; M_Z}{R^2} [/math]
jest siłą dośrodkową, konieczną do utrzymania satelity na orbicie. Przyrównując do ogólnego wyrażenia na siłę dośrodkową:
- [math] G \; \frac {m\; M_Z}{R^2} \; = \; m \; \frac {V^2}{R} [/math]
Otrzymujemy wyrażenie na prędkość satelity
- [math] V \; = \; \sqrt{\frac {G\; M_Z}{R}} [/math]
W przypadku satelity krążącego tuż nad powierznią Ziemi ([math]R=R_Z[/math]), jest to pierwsza prędkość kosmiczna:
- [math] V_1 \; = \; 7.91 \; km/s[/math]
Pierwsza prędkość kosmiczna to prędkość pozioma konieczna do "oderwania" od Ziemi (zaniedbując jej ruch wirowy)
Okres obiegu satelity dookoła Ziemi:
- [math] T \; = \; \frac{2\pi R}{V} [/math]
Podstawiając wyrażenie na prędkość otrzymujemy:
- [math] T \; = \; 2 \pi R \; \sqrt{\frac {R}{G\; M_Z}} \; = \; \frac{2 \pi R^{3/2}}{\sqrt{G\; M_Z}} [/math]
Oznacza to, że im wyższa orbita tym dłuższy okres obiegu...
Odwracając tą zależność:
- [math] R \; = \; \sqrt[3]{\frac {G\; M_Z \; T^2}{4 \pi^2 }} \; = \; \sqrt[3]{\frac {g\; R_Z^2 \; T^2}{4 \pi^2 }} [/math]
Dla okresu obiegu równego okresowi obrotu Ziemi
([math]23^h \; 56^m \; 4.09^s[/math])
otrzymujemy:
- [math] R \; = \; 42 \; 164 \; km [/math]
Jest to wysokość orbity satelity geostacjonarnego
Energia potencjalna
Siła grawitacji (jak każda siła centralna) jest zachowawcza. Praca wykonana przez siłę ciężkości zależy tylko od punktu początkowego i końcowego i wyraża się przez zmianę energii potencjalnej:
- [math] W_{AB} \; = \; \int\limits_A^B \vec{F}(\vec{r}) \cdot d\vec{r} \; = \; \int\limits_{r_A}^{r_B} - F(r) \cdot dr \; = \; - \Delta E_p [/math]
Podstawiając wzór na siłę grawitacji:
- [math] \Delta E_p \; = \; \int\limits_{r_A}^{r_B} G\; \frac{M \; m}{r^2} \cdot dr \; = \; \left[ - \frac{G \; M \; m}{r} \right]_{r_A}^{r_B} [/math]
Wnioskujemy, że energia potencjalna masy [math]m[/math] w polu grawitacyjnym masy [math]M[/math] wyraża się wzorem:
- [math] E_p(r)\; = \; - \;\frac{G \; M \; m}{r} \; + \; C [/math]
i jest określona z dokladnością do stałej [math]C[/math].
Zwyczajowo przyjmuje się [math]C =0[/math], co jest równoważne ustaleniu
- [math]E_p(\infty) \; = \; 0[/math]
Ruch w polu siły centralnej
Rozważmy przypadek ogólny ruchu punktu materialnego o masie [math]m[/math] w polu centralnej siły zachowawczej [math]\vec{F} = F(r) \cdot \vec{i}_r [/math]
Wiemy już, że w takim przypadku spełnione są
- zasada zachowania energii:
- [math] E \; = \; \frac{m v^2}{2} \; + \; E_p(r) \; = \; const[/math]
- zasada zachowania momentu pędu:
- [math] \vec{L} \; = \; m \vec{r} \times \vec{v} \; = \; const[/math]
Z zasady zachowanie momentu pędu wynika, że ruch będzie płaski (w płaszczyźnie [math]\vec{r}[/math] i [math]\vec{v}[/math]). Możemy zapisać wektor prędkości we współrzędnych biegunowych:
- [math]\vec{v} \; = \; \vec{i}_r \cdot \frac{dr}{dt} + \vec{i}_\theta \cdot r \frac{d\theta}{dt}[/math]
Co prowadzi do wyrażenia na kwadrat prędkości:
- [math] v^2 \; = \; \left(\frac{dr}{dt}\right)^2 \; + \; r^2 \; \omega^2 [/math]
Wstawiając to do wyrażenia na energię kinetyczną otrzymujemy:
- [math] E \; = \; E_k + E_p \; = \; \frac{m}{2} \left(\frac{dr}{dt}\right)^2\; + \; \frac{L^2}{2 \; m \;r^2} + E_p(r) \; = \; \frac{m}{2} \left(\frac{dr}{dt}\right)^2 + E_p^{e\!f\!f}(r) [/math]
gdzie skorzystaliśmy z wyrażenia na moment pędu [math]L \; = \; m \;r^2 \; \omega [/math]
Otrzymaliśmy dzięki temu równanie różniczkowe dla współrzędnej radialnej. Problem został tym samym zredukowany do problemu jednowymiarowego.
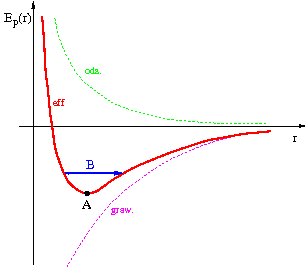
Energia efektywna
Aby rozważać ruch w polu siły centralnej jak problem jednowymiarowy wprowadzamy "efektywną" energia potencjalną:
- [math]E_p^{e\!f\!f}(r) \; = \; \; \; \frac{L^2}{2 \; m \;r^2}\;\; + \;E_p(r) [/math]
gdzie piewszy człon można rozumieć jako efektywną "energię odśrodkowa". Jeśli [math]L \ne 0[/math] to zasada zachowania momentu pędu "przeciwstawia się" zbliżeniu ciała do źródła siły ([math]r=0[/math]). Jest to tzw. bariera centryfugalna.
Wprowadzony człon "energii odśrodkowej" można też postrzegać jako energię potencjalną związaną z siłą odśrodkową (w nieinercjalnym układzie odniesienia współobracajacym się wokół centrum siły):
- [math] F_o \; = \; - \frac{d}{dr} \left( \frac{L^2}{2 \; m \;r^2} \right) \; = \; \frac{L^2}{m \; r^3} \; = \; m\; r \left( \frac{d\theta}{dt} \right)^2 [/math]
Ruch radialny
Jednowymiarowe zagadnienie ruchu radialnego wyprowadzone powyżej można przekształcić do postaci:
- [math] \frac{dr}{dt} \; = \; \sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r)\right)} [/math]
Pozwala to na rozdzielenie zmiennych i odcałkowanie zależności:
- [math] t \; = \; \int\limits_{r_\circ}^{r} \frac{dr'}{\sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r')\right)}}[/math]
Bez dalszych rachunków widzimy, że ruch może się odbywać tylko w obszarze [math]E - E_p^{e\!f\!f}(r) \ge 0[/math]
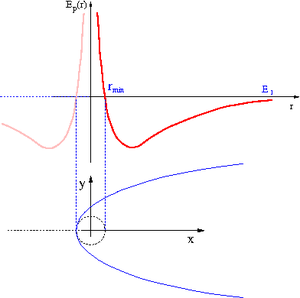
Jeśli moment pędu jest różny od zera, [math]L\ne 0[/math], istnieje (w przypadku oddziaływań grawitacyjnych; teoretycznie można wymyśleć siłę centralną silniejszą od siły odśrodkowej) ograniczenie na odległość najmiejszego zbliżenia ciała do centrum siły: [math]r \ge r_{min}[/math].
Jeśli całkowita energia ciała jest mniejsza niż graniczna wartość energii potencjalnej dla dużych odległości, [math]E \lt E_p^{e\!f\!f}(\infty)[/math], to ciało nie może dowolnie oddalić się od centrum siły i ruch odbywa się w ograniczonym obszarze, [math]r \le r_{max}[/math].
Ruch kątowy
W ruchu w polu sił centralnych moment pędu, [math]L \; = \; m \;r^2 \; \omega [/math], jest zachowany. Możemy wyrazić prędkość kątową przez moment pędu:
- [math] \omega \; = \; \frac{d\theta}{dt} \; = \; \frac{L}{ m \;r^2 } [/math]
Całkując otrzymujemy wyrażenie na zmianę kąta biegunowego:
- [math] \theta - \theta_\circ \; = \; \int\limits_0^{t} \frac{L}{ m \;r^2 } \; dt' [/math]
Możemy wyprowadzić równanie na tor ciała porównując zależności od czasu w ruchu radialnym i kątowym:
- [math] dt \; = \; \frac{dr}{\sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r)\right)}} \; = \; \frac{ m \;r^2 }{L} \; d\theta [/math]
Prowadzi to do ogólnego równania toru we współrzędnych biegunowych
- [math] \theta - \theta_\circ \; = \; \int \frac{L \; dr} {m \; r^2 \; \sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r)\right)}} [/math]
Zmiana kąta biegunowego przy przejściu ciała od [math]r_{min}[/math] do [math]r_{max}[/math] wynosi
- [math] \Delta \theta \; = \; \int\limits_{r_{min}}^{r_{max}} \frac{L \; dr} {m \; r^2 \; \sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r)\right)}} [/math]
Tor będzie krzywą zamkniętą, jeśli ta zmiana będzie wymierną wielokrotnością kąta pełnego: [math]\Delta \theta \; = \; 2 \pi \frac{m}{n}[/math] ([math]m[/math], [math]n[/math] - liczby całkowite).
Warunek ten spełniony jest (niezależnie od warunków początkowych) tylko dla dwóch typów pól:
- [math]E_p(r) \sim \frac{1}{r}[/math] - siła grawitacyjna, siła kulombowska
- [math]E_p(r) \sim r^2[/math] - siły sprężystości
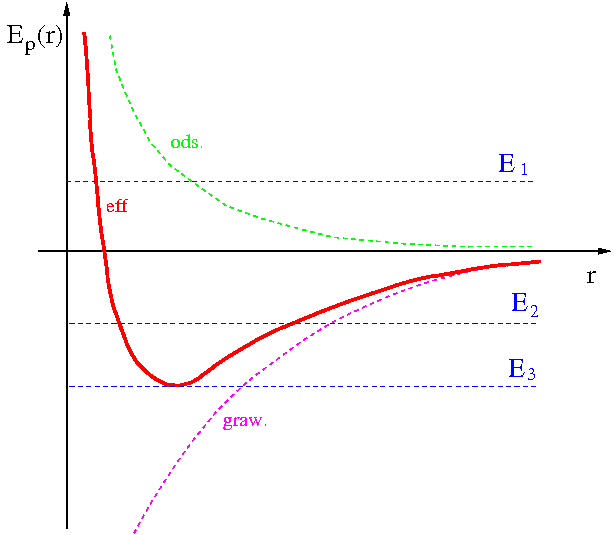
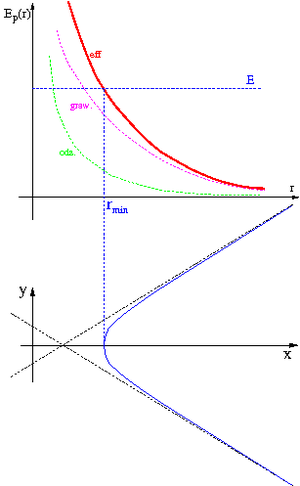
Ruch w polu grawitacyjnym
W polu grawitacyjnym opisanym prawem powszechnego ciążenia Newtona, zależność energii potencjalnej od odległości można przedstawić ogólnym wzorem:
- [math] E_p(r) \; = \; - \frac{k}{r} [/math]
gdzie współczynnik [math]k\gt 0[/math] (siła przyciągająca) oraz wybieramy [math]E_p(\infty) = 0[/math]
Charakter ruch ciała w tym polu zależy od jego energii całkowitej. Rysunek obok pokazuje trzy możliwe przypadki:
- [math]E_1 \gt 0[/math] - tor otwarty
- [math]E_2 \lt 0[/math] - tor zamknięty
- [math]E_3 = E_{min}[/math] - ruch po okręgu
Równanie toru
Wstawiając wzór na energię potencjalną w polu grawitacyjnym do wyrażenia na energi efektywną możemy rozwiązać wyprowadzone powyżej równanie toru:
- [math]\theta - \theta_\circ \; = \; \int \frac{L \; dr}
{m \; r^2 \; \sqrt{\frac{2}{m} \left( E - E_p^{e\!f\!f}(r)\right)}} [/math]
- [math]\; = \; \int \frac{ \frac{dr}{r^2}} {\sqrt{\frac{2m}{L^2} \left( E + \frac{k}{r} - \frac{L^2}{2mr^2}\right)}} [/math]
- [math] \; = \; - \int \frac{ d\left(\frac{1}{r}\right)} {\sqrt{\frac{2mE}{L^2} + \frac{2mk}{L^2}\left(\frac{1}{r}\right) - \left(\frac{1}{r}\right)^2 }} [/math]
- [math]\; = \; - \int \frac{ d\left(\frac{1}{r} - \frac{1}{p}\right)} {\sqrt{\frac{\varepsilon^2}{p^2} - \left(\frac{1}{r} - \frac{1}{p}\right)^2 }} [/math]
Gdzie wprowadziliśmy parametry: [math]p = \frac{L^2}{mk}[/math] oraz [math]\varepsilon = \sqrt{1 + \frac{2EL^2}{mk^2}}[/math]
Otrzymaliśmy dla zmiennej [math]u = \frac{1}{r} - \frac{1}{p}[/math] całkę postaci:
- [math] - \int \frac{du}{\sqrt{a^2 - u^2}}\; = \; \arccos \left( \frac{u}{a} \right)[/math]
gdzie [math]a = \frac{\varepsilon^2}{p^2} [/math]
Ostatecznie, po odwróceniu zależności, otrzymujemy:
- [math]r(\theta) \; = \; \frac{p}{1 + \varepsilon \cdot \cos ( \theta - \theta_\circ)}[/math]
Jest to ogólne równanie dla krzywej stożkowej (we współrzędnych biegunowych)
Parametr [math]\varepsilon[/math] - nazywamy mimośrodem orbity
Kształt toru zależy od wartości mimośrodu:
- dla [math]\varepsilon =0 [/math] ruch odbywa się po okręgu o promieniu [math]p[/math]
- dla wartości [math]0 \lt \varepsilon \lt 1 [/math] mamy do czynienia z ruchem po elipsie (całkowita energia [math]E\lt 0[/math])
- dla wartości [math]\varepsilon = 1 [/math] torem ruchu jest parabola (odpowiada to granicznemu przypadkowi [math]E=0[/math])
- dla [math]\varepsilon \gt 1 [/math] torem ruchu jest hiperbola ([math]E\gt 0[/math])
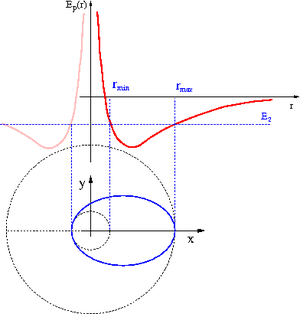
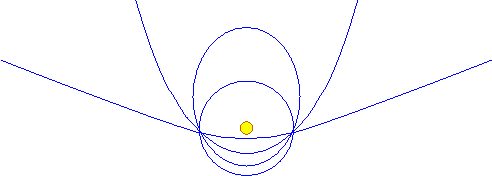
Ruch po elipsie
Z ruchem po elipsie mamy do czynienia gdy spełniony jest warunek:
- [math]E_{min} \; \lt \; E \; \lt \; 0[/math]
gdzie
- [math] E_{min} \; = \; -\frac{m\; k^2}{2\; L^2} [/math]
jest minimalną energią całkowitą przy ustalonej wartości momentu pędu [math]L[/math].
Ruch w tym przypadku ograniczony jest do
- [math]r_{min} \; \lt \; r \; \lt \; r_{max}[/math]
gdzie wartości [math]r_{min}[/math] i [math]r_{max}[/math] spełniają warunek
- [math]E_p^{e\!f\!f}(r_{min})=E_p^{e\!f\!f}(r_{max})=E[/math]
Źródło siły znajduje się w jednym z ognisk elipsy.
Osie elipsy:
- długa oś
- [math]2a = \frac{2p}{1-\varepsilon^2} = \frac{k}{2|E|}[/math]
- zależy wyłącznie od energii całkowitej, nie zależy od momentu pędu (!)
- [math]2a = \frac{2p}{1-\varepsilon^2} = \frac{k}{2|E|}[/math]
- krótka oś
- [math]2b = \frac{2p}{\sqrt{1-\varepsilon^2}} = \frac{L}{\sqrt{2m|E|}}[/math]
- determinuje "spłaszczenie" elipsy i zależy od momentu pędu
- [math]2b = \frac{2p}{\sqrt{1-\varepsilon^2}} = \frac{L}{\sqrt{2m|E|}}[/math]
parametry_elipsy.png
[math]\varepsilon = \frac{r}{AB}[/math]
W przypadku [math]L\rightarrow 0[/math] mamy ruch
po odcinku o długości [math]2a = \frac{k}{2|E|}[/math]; [math]b=0[/math]. Centrum siły (punktowe) znajduje się wtedy w jednym z końców
tego odcinka.
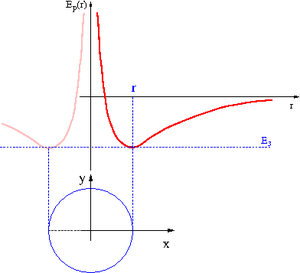
Ruch po okręgu
Przypadek szczególny: [math]\varepsilon =0 [/math]
- [math] E \; = \; E_{min} \; = \; -\frac{m\; k^2}{2\; L^2} [/math]
Energia całkowita jest równa minimalnej energii dopuszonej przy ustalonym [math]L[/math].
Moment pędu jest równy maksymalnemu momentowi dopuszczonemu przy ustalonej energii całkowitej.
Prawa Keplera
Zostały sformułowane w latach 1609-1619 na podstawie szczegółowych obserwacji astronomicznych:
- Każda planeta krąży po elipsie ze Słońcem w jednym z jej ognisk
- Promień wodzący każdej planety zakreśla równe pola w równych czasach
- Kwadrat okresu obiegu każdej planety wokół Słońca jest proporcjonalny do sześcianu półosi wielkiej elipsy
Pierwsze dwa prawa zostały już uzasadnione powyżej. Okres obiegu planety dookoła Słońca możemy wyznaczyć znając prędkość polową
- [math]\frac{dS}{dt} = \frac{L}{2m}[/math]
przy czym pole elipsy możemy wyrazić poprzez długości jej osi
- [math]2a = \frac{k}{2|E|} \; \; \; \; \; 2b = \frac{L}{\sqrt{2m|E|}}[/math]
Otrzymujemy:
- [math] T = \frac{S}{\left(\frac{dS}{dt}\right)} \; = \; \frac{\pi \; a \; b}{\frac{L}{2m}} \; = \; \pi k \;\sqrt{\frac{m}{2|E|^3}} [/math]
Podnosząc otrzymane wyrażenie do kwadratu
- [math] T^2 \; = \; \frac{\pi^2 k^2 m}{2|E|^3} \; = \; \frac{4\pi^2 m}{k} \cdot a^3 [/math]
Ruch po paraboli
Jest to także (podobnie jak ruch po okręgu) przypadek szczególny. Z ruchem po paraboli mamy do czynienia wtedy, gdy energia całkowita równa jest energii efektywnej w nieskończonej odległości od źródła (którą dla uproszczenia przyjęliśmy jako 0):
- [math]E = E_p(\infty) = 0[/math]
Ruch jest nieskończony i ciało nie jest związane przez centrum siły. Jednak oddalając sie do nieskończoności ciało będzie poruszać się coraz wolniej, asymptotycznie zatrzyma się.
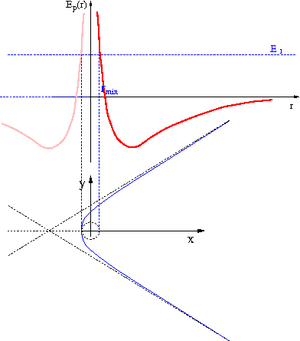
Ruch po hiperboli
Dla energii całkowitej [math]E \gt 0 [/math]
ruch jest nieskończony a torem ruchu
jest hiperbola.
Przykładem są orbity komet nieperiodycznych.
Asymptpotycznie prędkość ciała dąży do
- [math] v_\infty \; = \; \sqrt{\frac{2E}{m}} \; \gt \; 0 [/math]
Im mniejsze [math]L[/math] tym mniejsza odległość zbliżenia do centrum siły [math]r_{min}[/math]
Podsumowanie
Kształt w polu centralnej siły grawitacyjnej orbity zależy od
- energii całkowitej [math]E[/math] i
- momentu pędu ciała [math]L[/math]
Te dwa parametry decydują o kształcie toru opisywanym przez mimośród orbity
- [math]\varepsilon = \sqrt{1 + \frac{2EL^2}{mk^2}}[/math]
Dla ustalonej wartości [math]L[/math] możemy otrzymać różne kształty orbity, zależnie od wartości [math]E[/math]
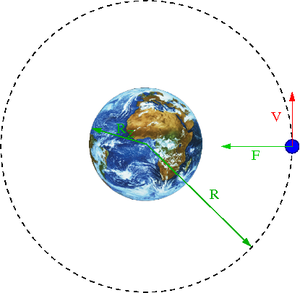
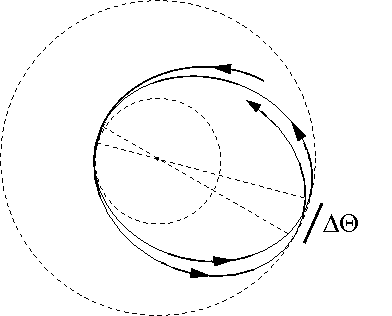
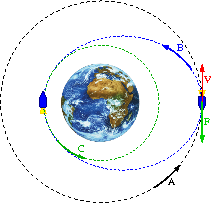
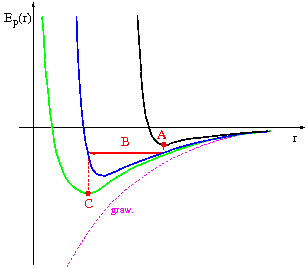
Ruch satelity
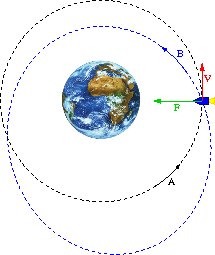
Jak powinien się zachować kosmonauta w rakiecie na orbicie kołowej, jeśli chce zbliżyć się do powierzchni Ziemi?
Odpalenie silników w kierunku Ziemi daje efekt przeciwny do zamierzonego!
Ponieważ moment pędu jest zachowany (siła radialna), [math]L=const[/math], a energia całkowita [math]E[/math] rośnie to rośnie też średnia odległość od Ziemi!
Widać to bardzo dobrze na wykresie energii efektywnej:
Lepszym sposobem na przejście na niższą orbitę jest włączenie silników hamujących
W tym przypadku moment pędu [math]L[/math] maleje i energia całkowita [math]E[/math] maleje . W rezultacie także średnia odległość od Ziemi maleje
Powtórne hamowanie po połowie obiegu umożliwia przejście na niższą orbitę kołową, odpowiadającą niższej energii całkowitej:
Doświadczenie Rutherforda
Potencjał odpychający
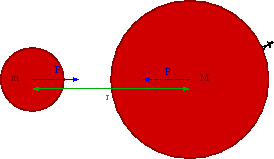
Rozważmy teraz ruch w potencjale odpychającym
- [math]\displaystyle E_p(r) \; = \; +\frac{k}{r}[/math], gdzie [math]k\gt 0[/math]
Uzyskane poprzednio rozwiązanie pozostaje formalnie słuszne, z dokładnością
do zmiany znaku przed parametrem [math]k[/math],
a co za tym idzie, zmiany znaku
parametru [math]p[/math]
Otrzymujemy zatem rozwiązenie w postaci:
- [math]r(\theta) \; = \; \frac{p}{\varepsilon \cdot \cos ( \theta - \theta_\circ)-1}[/math]
gdzie, jak porzednio
- [math]\varepsilon = \sqrt{1 + \frac{2EL^2}{mk^2}}[/math]
Teraz jednak energia całkowita jest zawsze dodatnia, [math]E \gt 0 [/math], a z tego wynika, że mimośród orbity [math]\varepsilon \gt 1 [/math].
Torem ruchu będzie więc zawsze hiperbola, im większe [math]\varepsilon [/math], tym większy kąt rozwarcia hiperboli.
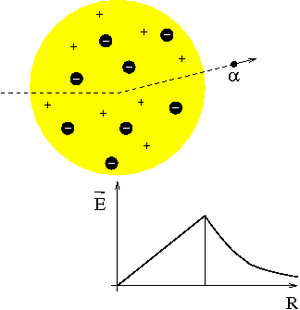
Model Thomson
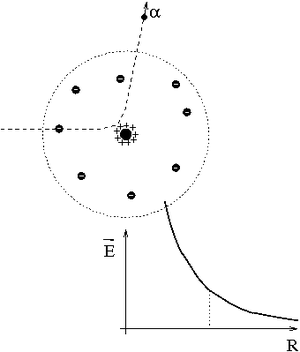
Po odkryciu elektronu (1897), J.J.Thomson zaproponował model atomu w postaci "ciastka z rodzynkami". Cała objętość atomu była jednorodnie naładowana dodatnio ("ciastko"), a wewnątrz "pływały" elektrony ("rodzynki").
Ponieważ ładunek był rozłożony równomiernie w dużej objętości, nie powinien silnie zakłócać ruchu przechodzący przez materię ciężkich cząstek [math]\alpha[/math]. Oczekujemy jedynie niewielkich odchyleń toru...
Także wpływ elektronów można zaniedbać ze względu na małą ich masę.
W modelu Thomsona można było oszacować maksymalny kąt rozproszenia cząstki [math]\alpha[/math] przechodzącej przez cienką folię i był on mały
- [math]\theta^{max} \ll \pi[/math].
Odpowiada to sytuacji rozproszenia "pocisku" na dużo lżejszej "tarczy" (masa przypadająca na jednostkę "rozmytego" ładunku atomu wynosiła ok. [math]\frac{1}{8}[/math] masy cząstki [math]\alpha[/math])
Doświadczenie Rutherforda
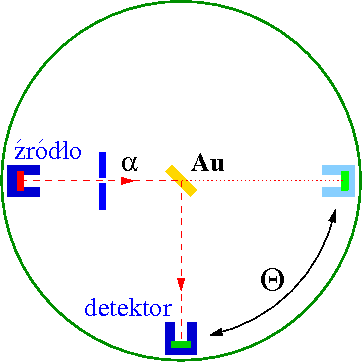
Doświadczenie z rozpraszaniem cząstek [math]\alpha[/math] na cienkiej złotej folii zostało przeprowadzone w laboratorium Rutherforda przez jego studentów H.Geigera i E.Marsdena w roku 1911. Obserwowali oni błyski wywoływane przez padające cząstki na ekranie scyntylacyjnym.
Pokaz
Dziś do obserwacji rozproszonych cząstek wykorzystujemy detektory z odczytem elektronicznym. Przykładowy układ detekcyjny wygląda następująco
Wiązka cząstek ze źródła jest dobrze skolimowana. Przed wsunięciem tarczy cząstki [math]\alpha[/math] obserwujemy więc tylko dla [math]\Theta \approx 0[/math].
Po umieszczeniu na drodze wiązki cienkiej foli złotej, oddziaływanie z tarczą zmniejsza strumień cząstek lecących "do przodu" ([math]\Theta \approx 0[/math]).
Rozproszone w wyniky oddziaływania cząstki [math]\alpha[/math] obserwujemy w szerokim zakresie kątów rozproszenia, także dla [math]\theta \ge \frac{\pi}{2}[/math].
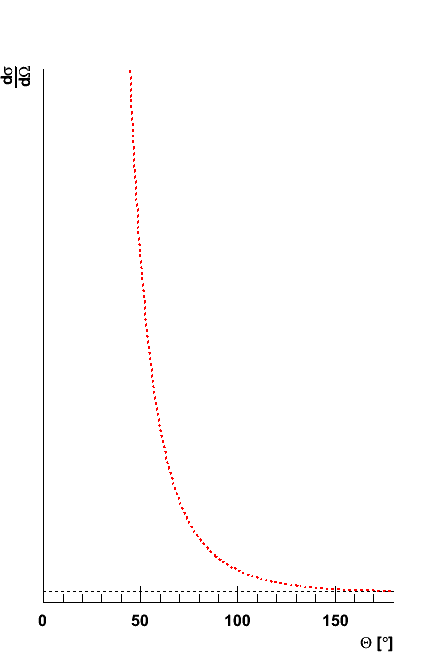
Wyniki pomiarów
Wyniki pomiarów przeprowadzonych przez H.Geigera i E.Marsdena (1911):
Zaobserwowano rozproszenia cząstek [math]\alpha[/math] pod bardzo dużymi kątami, [math]\theta \gg \theta^{max}_{Th}[/math], czego nie można było wyjaśnić w modelu Thomsona
"To było tak jakbyście wystrzelili piętnastocalowy pocisk w kierunku kawałka bibułki, a on odbił się i was uderzył."
E. Rutherford
Model Rutherforda
W oparciu o uzyskane wyniki Rutherford zaproponował jądrowy model atomu. Cały dodatni ładunek atomu ([math]10^{^{-10}}[/math]m) skupiony jest w praktycznie punktowym ([math]10^{^{-14}}[/math]m) jądrze.
Ponieważ cząstka [math]\alpha[/math] rozprasza się na jądrze jako całości, a masa jądra [math]M_{Au} \gg M_\alpha[/math] nie ma ograniczeń na kąt rozproszenia cząstki [math]\alpha[/math]. Kąty rozproszenia są dużo większe niż w modelu Thomsona, możliwe jest nawet (choć mało prawdopodobne) rozproszenie o [math]\theta \gt \pi/2[/math].
Obserwowany rozkład kątowy rozproszonych cząstek [math]\alpha[/math] jest proporcjonalny do tzw. rózniczkowego przekroju czynnego na rozpraszanie kulombowskie (wzór Rutherforda):
- [math] N(\theta) \; \sim \; \frac{d\sigma}{d\Omega} \; = \; \frac{Z^2 \alpha^2}{4 E^2 \sin^4 \frac{\theta}{2}} [/math]
Przewiduje on skończone prawdopodobieństwo nawet dla rozproszenia pod kątem [math]\theta = \pi[/math] ("odbicia" od tarczy) !

![Liczba obserwowanych cząstek [math]\alpha[/math] w funkcji kąta rozproszenia](/edu/images/e/e9/Rutherford_idea.png)