Matematyka 1 OO/Niestandardowe metryki

Zadanie

Znaleźć koło o promieniu [math]R[/math] i środku w początku układu współrzędnych w metryce “miejskiej” zadanej wzorem

[math] {\rm d}(A,B)=|x_B-x_A|+|y_B-y_A| [/math]

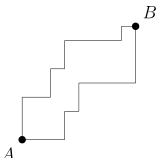
Warto wyjaśnić, skąd bierze się nazwa “metryka miejska”. Odległość między dwoma punktami [math]A[/math] i [math]B[/math] nie jest zwykłą długością odcinka łączącego te punkty, tylko długością krzywej łamanej złożonej z odcinków równoległych do jednej z osi układu współrzędnych. To odpowiada drodze, jaką musimy przebyć, jeśli możemy się poruszać tylko ulicami, z których każda ma kierunek wschód-zachód lub północ-południe.

Suma długości odcinków poziomych jest równa różnicy współrzędnych [math]X[/math] obu punktów, a suma długości odcinków pionowych jest równa różnicy współrzędnych [math]y[/math].

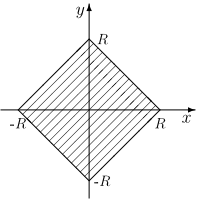
Szukane koło składa się z punktów [math]A[/math] spełniających warunek

[math] {\rm d}(A,O)=|x_A|+|y_A|\le R [/math]

Zacznijmy od okręgu o promieniu [math]r[/math]:

[math] |x_A|+|y_A|=r [/math]

Najłatwiej jest rozwiązać to równanie po kolej w każdej ćwiartce układu współrzędnych

a)	[math]x\gt 0,\,\,y\gt 0[/math]:	[math]x+y=r[/math]	[math]\Rightarrow [/math]	[math]y=-x+r[/math]
b)	[math]x\gt 0,\,\,y\lt 0[/math]:	[math]x-y=r[/math]	[math]\Rightarrow [/math]	[math]y=x-r[/math]
c)	[math]x\lt 0,\,\,y\lt 0[/math]:	[math]-x-y=r[/math]	[math]\Rightarrow [/math]	[math]y=-x-r[/math]
d)	[math]x\lt 0,\,\,y\gt 0[/math]:	[math]-x+y=r[/math]	[math]\Rightarrow [/math]	[math]y=x+r[/math]

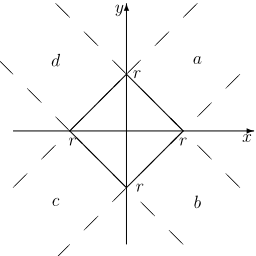
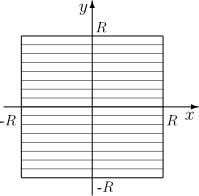
Rysujemy wykresy wszystkich czterech linii prostych zadanych równaniami [math]y=\mp x \mp r[/math] i na każdej z nich zaznaczmy odcinek spełniający odpowiedni warunek na znaki [math]x[/math] i [math]y[/math]

Koło o promieniu [math]R[/math] jest sumą okręgów o promieniach [math]r\le R[/math]

Zadanie

Znaleźć koło o promieniu [math]R[/math] i środku w początku układu współrzędnych w metryce “max” zadanej wzorem

[math] {\rm d}(A,B)=\max \left\lbrace |x_B-x_A|,|y_B-y_A|\right\rbrace [/math]

Takie koło składa się z punktów [math]A[/math] spełniających warunek

[math] {\rm d}(A,O)=\max \left\lbrace |x_A|,|y_A|\right\rbrace \le R [/math]

Zacznijmy od okręgu o promieniu [math]r[/math]:

[math] \max \left\lbrace |x_A|,|y_A|\right\rbrace =r [/math]

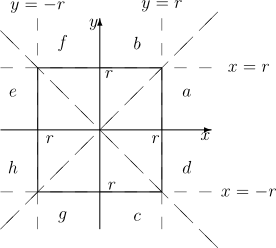
To równanie rozwiązujemy po kolej w każdej ćwiartce układu współrzędnych. Dodatkowa komplikacja polega na tym, że każdą ćwiartkę musimy podzielić na dwa obszary: [math]|x|\gt |y|[/math] i [math]|x|\lt |y|[/math].

a)	[math]x\gt y\gt 0[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|x|=x[/math]	[math]\Rightarrow [/math]	[math]x=r[/math]
b)	[math]y\gt x\gt 0[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|y|=y[/math]	[math]\Rightarrow [/math]	[math]y=r[/math]
c)	[math]|y|\gt x\gt 0\gt y[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math]	[math]\Rightarrow [/math]	[math]y=-r[/math]
d)	[math]x\gt 0\gt y\gt -|x|[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|x|=x[/math]	[math]\Rightarrow [/math]	[math]x=r[/math]
e)	[math]|x|\gt y\gt 0\gt x[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|x|=-x[/math]	[math]\Rightarrow [/math]	[math]x=-r[/math]
f)	[math]0\gt x\gt y[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math]	[math]\Rightarrow [/math]	[math]y=-r[/math]
g)	[math]0\gt x\gt y[/math]:	[math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math]	[math]\Rightarrow [/math]	[math]y=-r[/math]

Koło o promieniu [math]R[/math] jest sumą okręgów o promieniach [math]r\le R[/math]

Zadanie

Znaleźć koło o promieniu [math]R[/math] i środku w ustalonym punkcie [math]P=(x_P,y_P)[/math] w metryce “rzymskiej” zadanej wzorem

[math] {\rm d}(A,B)=\left\lbrace \begin{array}{ll} \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} & \exists _c\,\, [x_B,y_B]=c[x_A,y_A] \\[6pt] \sqrt{x_A^2+y_A^2}+\sqrt{x_B^2+y_B^2} & w innych przypadkach \end{array} \right. [/math]

Warunek w pierwszej linii powyższego wzoru opisuje przypadek, gdy punkty [math]A[/math] i [math]B[/math] leżą na jednej prostej przechodzącej przez początek układu współrzędnych (“Rzym”). Dla takich punktów ich wzajemna odległość jest równa zwykłej odległości euklidesowej [math]\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}[/math]. W innych przypadkach (dolna linia powyższego wzoru) odległość punktów [math]A[/math] i [math]B[/math] jest sumą odległości każdego z tych punktów od początku układu współrzędnych. (Jeśli dwa punkty leżą na różnych “drogach prowadzących do Rzymu”, to aby się dostać z jednego z nich do drugiego musimy przejechać przez “Rzym”).

Szukane koło składa się z punktów [math]A[/math] spełniających warunek

[math] {\rm d}(A,P)\le R [/math]

Jak zwykle, zacznijmy od okręgu o promieniu [math]r[/math]. W tym przypadku musimy być jednak bardziej uważni, niż w zadaniach poprzednich. Powodem jest to, że w metryce “rzymskiej” kształt koła zależy od jego promienia. Dla małych [math]r[/math], kołem (o środku różnym od początku układu współrzędnych) są dwa punkty leżące na półprostej łączącej dany punkt z początkiem układu współrzędnych, odległe od [math]P[/math] o [math]r[/math]:

[math] r=\sqrt{(x_A-x_P)^2+(y_A-y_P)^2} \qquad \qquad [x_A,y_A]=c[x_P,y_P] [/math]

Podstawiając drugie z tych równań do pierwszego, podniesionego stronami do kwadratu, dostajemy

[math] r^2 = (cx_P-x_P)^2+(cy_P-y_P)^2 = (c-1)^2(x_P^2+y_P^2) [/math]

Obliczamy stąd liczbę [math]c[/math]:

[math] (c-1)^2=\frac{r^2}{x_P^2+y_P^2} [/math]

[math] c-1=\pm \frac{r}{\sqrt{x_P^2+y_P^2}} [/math]

[math] c=1\pm \frac{r}{\sqrt{x_P^2+y_P^2}} [/math]

Wstawiając [math]c[/math] do warunku łączącego współrzędne punktu [math]A[/math] ze współrzędnymi punktu [math]P[/math] (warunek opisujący fakt, że [math]A[/math] i [math]P[/math] leżą na jednej półprostej zaczynającej się w środku układu współrzędnych)

[math] [x_A,y_A]=c[x_P,y_P] [/math]

otrzymujemy

[math]\begin{matrix} x_{A_\pm }=x_P\pm \frac{rx_P}{\sqrt{x_P^2+y_P^2}} \\ y_{A_\pm }=y_P\pm \frac{ry_P}{\sqrt{x_P^2+y_P^2}} \end{matrix}[/math]

Kształt koła o promieniu [math]r[/math] jest inny dla [math]r\gt \sqrt{x_P^2+y_P^2}[/math]. Punkty [math]A_-[/math] i [math]A_+[/math] nadal leżą na prostej [math]OP[/math], z tym, że [math]A_-[/math] znajduje się “po drugiej stronie” początku układu współrzędnych, co odpowiada ujemnej wartości współczynnika [math]c[/math]:

[math] c_-=1-\frac{r}{\sqrt{x_P^2+y_P^2}}\lt 0 [/math]

Okrąg o promieniu [math]r\gt \sqrt{x_P^2+y_P^2}[/math] zawiera jednak nie tylko punkty [math]A_-[/math] i [math]A_+[/math], ale także punkty niewspółliniowe z [math]O[/math] i [math]P[/math]. Położenie takich punktów znajdujemy korzystając ze wzoru na odległość punktów nie leżących na jednej “drodze” prowadzącej do “Rzymu”:

[math] d(A,P)=\sqrt{x_A^2+y_A^2}+\sqrt{x_P^2+y_P^2} [/math]

Przyrównujemy te odległość do [math]r[/math]:

[math] r=\sqrt{x_A^2+y_A^2}+\sqrt{x_P^2+y_P^2} [/math]

[math] x_A^2+y_A^2=\left(r-\sqrt{x_P^2+y_P^2}\right)^2 [/math]

Jest to zwykły okrąg o promieniu [math]r-\sqrt{x_P^2+y_P^2}[/math] i środku w początku układu współrzędnych.

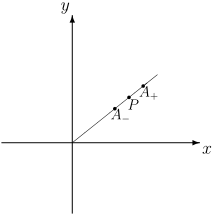
Okrąg w metryce “rzymskiej” o środku w punkcie [math]P=(x_P,y_P)[/math] i promieniu [math]r\gt \sqrt{x_P^2+y_P^2}[/math] jest sumą zwykłego okręgu o środku w początku układu współrzędnych i promieniu [math]r-\sqrt{x_P^2+y_P^2}[/math] i punktu [math]A_+[/math] leżącego na półprostej [math]OP[/math] w odległości [math]r[/math] od punktu [math]P[/math].

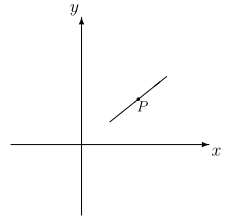
Znając kształty okręgów, możemy wyznaczyć postać kół o środku w punkcie [math]P=(x_P,y_P)[/math]. Jeśli promień koła [math]R[/math] jest nie większy niż [math]\sqrt{x_P^2+y_P^2}[/math], to kołem o tym promieniu jest suma “dwupunktowych” okręgów o [math]r\le R[/math], czyli

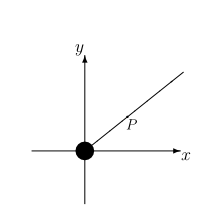
Jeśli promień [math]R[/math] przekracza wartość [math]\sqrt{x_P^2+y_P^2}[/math], koło jest sumą odcinka i zwykłego koła o środku w początku układu współrzędnych i promieniu [math]R-\sqrt{x_P^2+y_P^2}[/math]

Na koniec pozostaje rozpatrzeć przypadek, gdy środek okręgu [math]P[/math] pokrywa się z początkiem układu współrzędnych [math]O[/math]. W takim przypadku odległość w metryce “rzymskiej” sprowadza się do odległości euklidesowej

[math] d(A,O)=\sqrt{x_A^2+y_A^2} [/math]

i koło o promieniu [math]R[/math] jest zwykłym kołem o takim samym promieniu i środku w początku układu współrzędnych.

Zadanie

Warto zrobić proste zadanie, które pokazuje, że mówienie o różnych metrykach nie jest tylko “akademicką zabawą”. Można np. zadać pytanie: jaka jest odległość z Gdyni do Kapsztadu. Przyjmujemy następujące dane: oba miasta mają taką samą długość geograficzną (około [math]18^{\circ }30^{\prime }[/math]E), a szerokości geograficzne odpowiednio [math]54^{\circ }30^{\prime }[/math]N i [math]34^{\circ }[/math]S, natomiast promień Ziemi wynosi [math]R=6370[/math] km.

Odpowiedzi na pytanie od odległość między tymi dwoma miastami mogą być aż trzy:

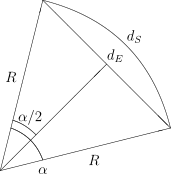
1. Oba miasta leżą na jednym południku, który jest (w przybliżeniu) okręgiem o promieniu [math]R[/math]. Kąt między promieniami tego okręgu przechodzącymi przez te miasta wynosi [math]\alpha =54,5^\circ +34^\circ =88,5^\circ [/math]. Odległość w trójwymiarowej przestrzeni euklidesowej wynosi więc

   [math] d_E=2R\sin \left(\frac{\alpha }{2}\right) [/math]

   Taka odległość odpowiada długości prostoliniowego tunelu łączącego oba miasta (gdyby taki tunel istniał).
2. Odległość mierzona wzdłuż okręgu, czyli po powierzchni Ziemi wynosi

   [math] d_S=R\alpha ,\, [/math]

   gdzie kąt [math]\alpha [/math] jest wyrażony w radianach

   [math] \alpha =\pi \frac{88,5}{180} [/math]

   Oczywiście odległość po okręgu (po powierzchni Ziemi) jest większa od odległości po cięciwie (wzdłuż tunelu)

   [math] \sin \left(\frac{\alpha }{2}\right)\lt \frac{\alpha }{2} \qquad \Rightarrow \qquad d_E\lt d_S [/math]

   
3. Odległość między dwoma portami można też zdefiniować, jako długość drogi, jaką musi przebyć statek. Jest ona większa od obu poprzednich odległości i na dodatek dość skomplikowana (zależy od kształtu i położenia kontynentów).

Odległości a) i b) można opisać dwiema metrykami na okręgu (wydaje się, że wprowadzanie metryki na sferze może być zbyt skomplikowane dla słuchaczy tych zajęć):

[math] d_E(\phi _1,\phi _2)=2R\sin \left(\frac{\phi _2-\phi _1}{2}\right),\, [/math]

[math] d_S(\phi _1,\phi _2)=R|\phi _1-\phi _2|,\, [/math]

gdzie [math]\phi _i[/math] są wartościami wspołrzędnej kątowej opisującej położenie danych punktów na okręgu.