WnioskowanieStatystyczne/Analiza wariancji
Wnioskowanie_Statystyczne_-_wykład
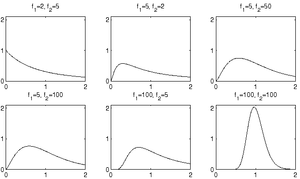
Rozkład F
Niech zmienne [math]x[/math] i [math]y[/math] mają rozkłady [math]\chi ^{2}[/math] o odpowiednio [math]f_{1}[/math] i [math]f_{2}[/math] stopniach swobody. Zmienna
[math] F=\frac{\frac{1}{f_{1}} x}{\frac{1}{f_{2}}y}=\frac{f_{2}x}{f_{1}y} [/math]
posiada rozkład [math]F[/math] z [math]f_{1}[/math] i [math]f_{2}[/math] stopniami swobody (wartość oczekiwana [math]E(f)=\frac{f_{2}}{(f_{2}-2)}[/math])
[math] f(F)=\left( \frac{f_{1}}{f_{2}}\right) ^{\frac{f_{1}}{2}}\frac{\Gamma \left( \frac{1}{2}\left( f_{1}+f_{2}\right) \right) }{\Gamma \left( \frac{f_{1}}{2} \right) \Gamma \left( \frac{f_{2}}{2}\right) }F^{\frac{f_{2}}{2}-1}\left( 1+ \frac{f_{1}}{f_{2}}F\right) ^{-\frac{f_{1}+f_{2}}{2}} [/math]
Dla próby z rozkładu normalnego wielkość
[math] \chi ^{2}=\underset{i=1}{\overset{N}{\sum }}\frac{(x_{i}-\overline{x})^{2}}{ \sigma ^{2}} [/math]
podlega rozkładowi [math]\chi ^{2}[/math] o [math]f=N-1[/math] stopniach swobody. Jeśli dwie takie próby zostały pobrane z jednej populacji, to iloraz
[math] F=\frac{\left( N_{y}-1\right) \underset{i=1}{\overset{N}{\sum (}}x_{i}- \overline{x})^{2}}{\left( N_{x}-1\right) \underset{i=1}{\overset{N}{\sum }} (y_{i}-\overline{y})^{2}} [/math]
podlega rozkładowi [math]F[/math] o [math]f_{y}[/math] i [math]f_{x}[/math] stopniach swobody.
Wielokrotne porównania
[math]N[/math] obserwacji podzielonych na 7 grup. Testujemy hipotezę, że średnie tych grup są równe -- czyli niejako przyporządkowanie do grup jest przypadkowe. Możemy wykonać [math]\binom{7}{2}=21[/math] testów różnic między grupami. Jeśli przyjmiemy poziom istotności 0.05 ...
Problem wielokrotnych porównań (ang. multiple comparisons) pojawia się w eksploracyjnej (w odróżnieniu od konfirmacyjnej) analizie danych, kiedy np. nie wiemy gdzie oczekiwać różnic.
Korekcja Bonferroniego polega na podzieleniu poziomu istotności przez liczbę porównań. Jest mocno konserwatywna.
por. http://en.wikipedia.org/wiki/Data_dredging zwane też [math]p[/math]-hacking.
Analiza wariancji (ANalysis of VAriance — ANOVA)
[math]N[/math] obserwacji [math]\{x_{i}\}_{i=1..N}[/math] podzielonych na [math]k[/math] grup wedle jakiegoś kryterium: [math]N=n_{1}+n_{2}+...+n_{k}[/math]. Średnie wewnątrz grup
[math] \overline{x}_{i}=\frac{1}{n_{i}}\underset{j=1}{\overset{n_{i}}{\sum }}x_{ij} [/math]
Rozważmy sumę kwadratów odchyleń wszystkich elementów próby od wartości średniej całej próby:
[math]\begin{matrix} \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{ \overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i}+\overline{x}_{i}-\overline{x} )^{2}=\\ =\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{\overset{k}{\sum }}\underset{j=1 }{\overset{n_{i}}{\sum }}(\overline{x}_{i}-\overline{x})^{2}+2\underset{i=1}{ \overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x} _{i})(\overline{x}_{i}-\overline{x}) \end{matrix}[/math]
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x}_{i})(\overline{x}_{i}-\overline{x})=\underset{i=1}{ \overset{k}{\sum }}(\overline{x}_{i}-\overline{x})\underset{j=1}{\overset{ n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})=0 [/math]
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }}( \overline{x}_{i}-\overline{x})^{2}=\underset{i=1}{\overset{k}{\sum }}n_{i}( \overline{x}_{i}-\overline{x})^2 [/math]
[math] \underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i}}{\sum }} (x_{ij}-\overline{x}_{i})^{2}=\underset{i=1}{\overset{k}{\sum }}\underset{j=1 }{\overset{n_{i}}{\sum }}(x_{ij}-\overline{x}_{i})^{2}+\underset{i=1}{ \overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x} )^{2}=s_{wew}^{2}+s_{pom}^{2} [/math]
Jeśli wszystkie pomiary pochodzą z tej samej populacji o wariancji [math] \sigma ^{2}[/math], to
[math] \frac{s^2_{wew}}{\sigma ^{2}}\ i\ \ \frac{s^2_{pom}}{\sigma ^{2}} [/math]
podlegają rozkładom [math]\chi ^{2}[/math] o odpowiednio [math]n-k[/math] i [math]k-1[/math] stopniach swobody. Iloraz
[math] \frac{\left( n-k\right) s^2_{pom}}{\left( k-1\right) s^2_{wew}} [/math]
podlega rozkładowi [math]F[/math] o [math]k-1[/math] i [math]n-k[/math] stopniach swobody. Wyrażenia
[math] \frac{1}{n-k}\underset{i=1}{\overset{k}{\sum }}\underset{j=1}{\overset{n_{i} }{\sum }}(x_{ij}-\overline{x}_{i})^{2}\ oraz\ \ \frac{1}{k-1}\underset{i=1}{ \overset{k}{\sum }}n_{i}(\overline{x}_{i}-\overline{x})^{2} [/math]
czyli
[math] \frac{s_{wew}^{2}}{n-k}\ \ oraz\ \ \frac{s_{pom}^{2}}{k-1} [/math]
są nieobciążonymi estymatami wariancji populacji.