WnioskowanieStatystyczne/Bonferroni

Wnioskowanie_Statystyczne_-_wykład

Wielokrotne porównania

Niebranie pod uwagę problemu wielokrotnych porównań (ang. multiple comparisons) ilustruje jakościowo przykład z Wikipedii: http://en.wikipedia.org/wiki/Data_dredging

Przykład ilościowy

[math]N[/math] obserwacji podzielonych na 7 grup. Testujemy hipotezę o różnicy między średnimi dowolnych par grup, wykonując [math]\binom{7}{2}=21[/math] testów hipotez o różnicach między dwoma grupami.

Załóżmy, że podziału na 7 grup dokonaliśmy zupełnie przypadkowo, czyli że nie powinna wystąpić istotna statystycznie różnica między średnimi żadnej pary. Jeśli test dla każdej pary wykonujemy na poziomie istoności p=5%, to przyjmujemy, że z prawdopodobieństwem 0,05 test może wykazać różnicę (FP). Prawdopodobieństwo, że test nie wykaże różnicy, wynosi 1 - 0,05 = 0,95. Prawdopodobieństwo, że test poprawnie nie wykaże różnicy we wszystkich 21 porównaniach, wynosi (0,95)²¹ czyli ok. 0,34. Tak więc prawdopodobieństwo, że przynajmniej w jednej parze grup test fałszywie wykaże różnicę, pomimo wykonywania każdego testu na poziomie istotności 0,05 wynosi aż 1 - 0,34 = 0,66!

FWER: family-wise error rate

Poziomy istotności zdefiniowane dla pojedynczych testów zastępujemy pojęciem FWER, czyli prawdopodobieństwem popełnienia przynajmniej jednego błędu I rodzaju w grupie (rodzinie) testów.

Niech rodzina składa się z [math]m[/math] hipotez [math]\{H_i\}_{i=1..m}[/math], z których [math]m_0[/math] jest prawdziwych, a każdej z hipotez [math]H_i[/math] odpowiada prawdopodobieństwo [math]p_i[/math].

Poprawka Bonferroniego

gwarantuje, że jeśli każdy z m testów wykonamy na poziomie istotności [math]\frac{\alpha}{m}[/math], to [math]\mathrm{FWER}=\alpha[/math].

Dowód

Powtórzmy założenia: rozważamy rodzinę [math]m[/math] hipotez [math]H_i[/math], przypisując każdemu z testów odpowiadających [math]H_i[/math] p-wartość (ang. p-value) p_i. Niech [math]m_0 \le m[/math] z tych hipotez będzie prawdziwych.

Jeśli wszystkie hipotezy z rodziny będziemy testować na tym samym poziomie istotności [math]\frac{\alpha}{m}[/math], to pojedynczą hipotezę [math]H_i[/math] odrzucimy, jeśli [math]p_i\leq\frac{\alpha}{m}[/math].

W tej sytuacji [math]\mathrm{FWER}[/math], czyli prawdopodobieństwo popełnienia przynajmniej jednego błędu I rodzaju w którymś z [math]m_0[/math] testów prawdziwych hipotez [math]H_i[/math], będzie logiczną sumą [math]m_0[/math] takich zdarzeń

[math] \text{FWER} = P\left\{ \bigcup_{i=1}^{m_0}\left(p_i\leq\frac \alpha m \right) \right\}[/math]

i zgodnie z nierównością Boole'a będzie nie większe niż suma prawdopodobieństw popełnienia błędu I rodzaju [math] \sum_{i=1}^{m_0} P\left(p_i\leq\frac \alpha m\right)[/math] w każdym testów z osobna:

[math] P\left\{ \bigcup_{i=1}^{m_0}\left(p_i\leq\frac \alpha m \right) \right\} \leq \sum_{i=1}^{m_0} P\left(p_i\leq\frac \alpha m\right) = m_0 \frac{\alpha}{m}[/math]

Ponieważ nie wiemy a priori, ile z hipotez [math]H_i[/math] jest prawdziwych, nie znamy wartości [math]m_0[/math]. Wiemy tylko, że [math]m_0 \le m[/math], więc

[math]\mathrm{FWER} \leq m_0 \frac{\alpha}{m} \le m \frac{\alpha}{m} = \alpha[/math]

Jest to poprawka bardzo konserwatywna, wymuszająca przeprowadzanie testów na potencjalnie zaniżonych poziomach istotności [math]\frac{\alpha}{m}[/math].

Przykład

Sprawdźmy, jak poprawka Bonferroniego zadziała w opisanym powyżej przykładzie 7 grup: mamy 21 porównań, jeśli chcemy utrzymać prawdopodobieństwo co najmniej jednego błędu I rodzaju na poziomie 5%, każdy test musimy wykonać na poziomie [math]\frac{0.05}{21} \approx 0.002381[/math] czyli mniej niż 0,0024%! Wtedy prawdopodobieństwo popełnienia jednego błędu I rodzaju wyniesie

[math] 1 - \left( 1 - \frac{0,05}{21} \right)^{21} \approx 0,0488 [/math]

czyli mniej niż 0,05.

Analogiczny wynik dostaniemy np. dla tysiąca testów

[math] 1 - \left( 1 - \frac{0,05}{1000} \right)^{1000} \approx 0,0488 [/math]

ale wtedy każdy z testów musielibyśmy wykonywać na poziomie istotności 0,00005.

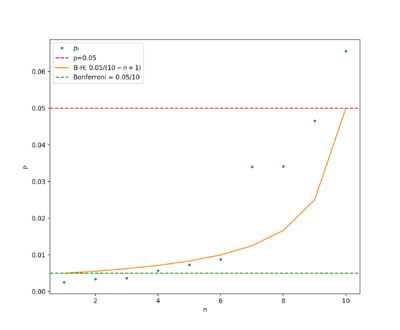
Poprawka Bonferroniego-Holma

gwarantuje, że jeśli każdy z [math]m[/math] testów wykonamy na poziomie [math] \frac{\alpha}{m+1-k}[/math], gdzie [math]k[/math] znajdujemy w opisanej poniżej procedurze, to [math]\mathrm{FWER} = \alpha[/math]

Znajdowanie [math]k[/math]

P-wartości p_i, odpowiadające hipotezom H_i, sortujemy w kolejności od najmniejszej do największej

p₍₁₎ < p₍₂₎ < ... < p_(m)

Dla [math]\textrm{FWER}=\alpha[/math] znajdujemy najmniejsze k, dla którego

[math]p_k \gt \frac{\alpha}{m+1-k}[/math]

i odrzucamy hipotezy H₁ ... H_k-1, przyjmując H_k ... H_m.

Dowód

Mamy dowieść, że prawdopodobieństwo popełnienia błędu I rodzaju w tej procedurze jest nie większe niż [math]\alpha[/math]. Ponownie zakładamy, że wśród [math]m[/math] testowanych [math]H_i[/math] jest [math]m_0[/math] hipotez prawdziwych. Jak w przepisie na znajdowanie [math]k[/math], hipotezy [math]H_i[/math] renumerujemy tak, żeby hipotezie [math]H_1[/math] odpowiadała najmniejsza wartość [math]p_i[/math].

Zacznijmy of [math]H_1[/math]. Jeśli odpowiadające jej [math]p_1 \lt \frac{\alpha}{m-1+1}[/math], odrzucamy [math]H_1[/math] i kontynuujemy do [math]H_2[/math].

Jeśli [math]p_2 \lt \frac{\alpha}{m-2+1}[/math], odrzucamy [math]H_2[/math] i kontynuujemy do [math]H_3[/math].

Niech pierwszą hipotezą, dla której [math]p_k \gt \frac{\alpha}{m-k+1}[/math] będzie [math]H_k[/math]. To znaczy, że odrzucamy hipotezy [math]H_1 \ldots H_{k-1}[/math], czyli wykazujemy [math](k-1)[/math] istotnych różnic, a [math]H_k[/math] jest pierwszą z przyjętych hipotez zerowych. Akceptujemy również [math](m-k+1)[/math] pozostałych hipotez [math]\{H_i\}_{i=k \ldots m}[/math].

[math]k - 1 \leq m - m_0 \\ m_0 \leq m - k + 1 \\ \dfrac{1}{m_0} \ge \dfrac{1}{m-k+1} [/math]

czyli również [math] \dfrac{\alpha}{m_0} \ge \dfrac{\alpha}{m-k+1} [/math]

Skoro [math]H_k[/math] została odrzucona, to z definicji procedury

[math] p_k \leq \frac{\alpha}{m - k +1} \leq \frac{\alpha}{m_0}[/math]

— odpowiada to poprawce Bonferroniego w zbiorze [math]m_0[/math] hipotez prawdziwych, czyli kontroluje [math]\mathrm{FWER}[/math] na poziomie [math]\alpha[/math].

False Discovery Rate FDR

...w podobnej procedurze kontroluje oczekiwany stosunek liczby hipotez błędnie odrzuconych do liczby hipotez odrzuconych.

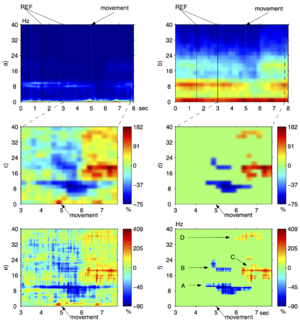
Poniżej przykład zastosowania z artykułu On the statistical significance of event-related EEG desynchronization and synchronization in the time-frequency plane. PDF.

Calculating the high-resolution ERD/ERS from the MP decomposition in statistically significant regions. (a) Average time-frequency energy density approximated from the MP decomposition. Reference epoch marked by black vertical lines, movement onset in the fifth second marked by white dashed line. (b) Energy from (a) integrated in resels 0.25 s x 2 Hz. (c) Average values of ERD/ERS calculated for the time from the end of the reference epoch to the end of the recorded epoch (black dashed vertical lines in (a) and (b)). (d) ERD/ERS from (c) indicated as statistically different from the reference epoch by the pseudo- bootstrap procedure (Section II-D3) corrected by a 5% FDR. (e) High-resolution map of ERD/ERS calculated from (a). (f) High-resolution ERD/ERS in statistically significant regions from (d). A— [math]\mu[/math] desynchronization, B—desynchonization of the [math]\mu[/math] harmonic, C—postmovement [math]\beta[/math] synchronization, D—harmonic of [math]\beta[/math]. Horizontal scales in seconds, vertical in Hz.

Evaluation of measurement data — Guide to the expression of uncertainty in measurement

JCGM 100:2008 GUM 1995 with minor corrections http://www.iso.org/sites/JCGM/GUM-JCGM100.htm

3.4.8 Although this Guide provides a framework for assessing uncertainty, it cannot substitute for critical thinking, intellectual honesty and professional skill. The evaluation of uncertainty is neither a routine task nor a purely mathematical one; it depends on detailed knowledge of the nature of the measurand and of the measurement. The quality and utility of the uncertainty quoted for the result of a measurement therefore ultimately depend on the understanding, critical analysis, and integrity of those who contribute to the assignment of its value.

Formalnym sposobem przeciwdziałania praktykom wybiórczego raportowania wyników jest prerejestracja badań.