FizykaI FMiN/Kinematyka
Kinematyka: opis ruchu
Pojęcia podstawowe
Punkt materialny
Ciało, którego rozmiary można w danym zagadnieniu zaniedbać.
Zazwyczaj przyjmujemy, że punkt materialny powinien być dostatecznie mały. Nie jest to jednak konieczne! Przykłady: wagon kolejowy na torach albo "wózek" na torze powietrznym. Ważne jest, żeby ciało nie miało dodatkowych "stopni swobody" (np. obroty, drgania własne, stany wzbudzone).
Położenie punktu materialnego całkowicie określa jego "stan".
[math]\Rightarrow[/math] pojęcie punktu materialnego umożliwia prosty opis wielu sytuacji fizycznych.
Naogół przyjmujemy, że punkt materialny obdarzony jest masą.
Ruch
Zmiana położenia ciała względem wybranego układu odniesienia.
Z punktu widzenia fizyki nie możemy nic powiedzieć o ruchu obserwowanego ciała póki nie odniesiemy go do jakiegoś innego obiektu. Oczywiście sami możemy uznać się za właściwy układ odniesienia, ale jest to wybór, który może istotnie wpłynąć na opisywany ruch…
Układ odniesienia
Musimy wybrać ciało, które potraktujemy jako "punkt odniesienia". Najczęściej jest nim Ziemia… Układ odniesienia można też zdefiniować określając jego położenie (lub ruch) względem wybranego ciała lub grupy ciał.
Przykład:
- układ środka masy zderzających się cząstek
- układ związany ze środkiem Galaktyki
Układ współrzędnych
Służy do określenia położenia ciała w danym układzie odniesienia.
Położenie możemy zapisać na wiele różnych sposobów:
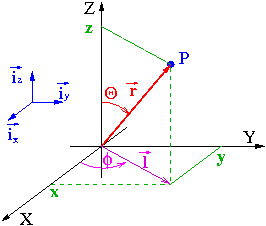
- układ współrzędnych kartezjańskich: [math]\begin{array}{rcl} \vec{r} & = & x\cdot \vec{i}_x + y\cdot \vec{i}_y + z\cdot \vec{i}_z \\ & \equiv & (x,y,z) \end{array}[/math]
- układ współrzędnych biegunowych: [math]\begin{array}{rcl} \vec{r} & = & (r,\Theta,\phi) \end{array}[/math]
- układ współrzędnych walcowych: [math]\begin{array}{rcl} \vec{r} & = & (l,\phi,z) \end{array}[/math]
Tor ruchu
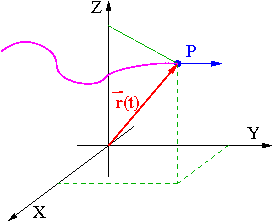
Opisuje zmianę położenia ciała w czasie. W ogólnym przypadku tor zapisujemy w tzw. postaci parametrycznej:
[math]\begin{array}{rcl} x \!\! & = & \!\! x(t) \;\;\;\; y = y(t) \;\;\;\; z = z(t) \\[5mm] \vec{r} & = & \left( x(t),y(t),z(t) \right) \; = \; \vec{r}(t) \end{array}[/math]
Wektor położenia ciała [math]\vec{r}[/math] (wszystkie jego współrzędne) wyrażamy jako funkcje czasu.
W szczególnych przypadkach możliwe jest odwrócenie jednej z zależności, na przykład:
[math]\begin{array}{rcl}t &=& F(x)\end{array}[/math]
Gdy czas wyrazimy jako funkcję współrzędnej możemy uzyskać postać uwikłaną toru:
[math]\begin{array}{rcl} y \!\! & = & \!\!y(F(x)) = y(x) \;\;\;\; z = z(x) \\[5mm] \vec{r} & = & \left( x,y(x),z(x) \right) \end{array}[/math]
Funkcje
W fizyce bardzo często staramy się opisać zależności pomiędzy różnymi wielkościami w postaci funkcyjnej. Na ogół do oznaczania funkcji używamy symbolu odpowiadającego danej wielkości fizycznej, np.:
- droga — s,
- wysokość — h,
- prędkość — v
Postać funkcyjna zależy jednak od wyboru argumentu funkcji! W przypadku opisu toru należy zauważyć, że [math]y(t)[/math] i [math]y(x)[/math] to dwie różne funkcje(!) choć opisują tą samą wielkość fizyczną.
Prędkość średnia
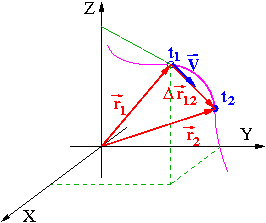
W odstępie czasu:
[math]\begin{array}{rcl}\Delta t_{12} & = & t_2 - t_1 \end{array}[/math]
punkt materialny przemieścił się o:
[math]\begin{array}{rcl}\Delta \vec{r}_{12} & = & \vec{r}_2 - \vec{r}_1 = \vec{r}(t_2) - \vec{r}(t_1) \end{array}[/math]
Prędkość średnią definiujemy jako
[math]\begin{array}{rcl} \vec{V}^{^\textrm{(śr)}}_{12} & = & \frac{\Delta \vec{r}_{12}}{\Delta t_{12}} \end{array}[/math]
Prędkość chwilowa
Praktycznie każdy pomiar prędkości musi trwać skończony okres czasu. Prawie zawsze mierzymy więc prędkość średnią.
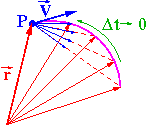
Pojęcie prędkości chwilowej wprowadzamy jako graniczną wartość prędkości średniej dla nieskończenie krótkiego czasu pomiaru, [math]\Delta t \rightarrow 0[/math]:
[math]\begin{array}{rcl} \vec{v} & = & \lim_{\Delta t \rightarrow 0}\; \frac{\Delta \vec{r}}{\Delta t} \end{array}[/math]
Matematycznie odpowiada to definicji pochodnej: [math]\begin{array}{rcl} \vec{v} & = & \frac{d \vec{r}}{d t} \;\; = \;\; \dot{\vec{r}} \;\; = \;\; \frac{d x}{d t}\cdot \vec{i}_x + \frac{d y}{d t}\cdot \vec{i}_y + \frac{d z}{d t}\cdot \vec{i}_z \;\; = \;\; v_x \cdot \vec{i}_x + v_y \cdot \vec{i}_y + v_z \cdot \vec{i}_z \end{array}[/math]
Pochodna wektora [math]\equiv[/math] wektor pochodnych składowych tego wektora
Wartość prędkości: [math]\begin{array}{rcl} v & = & | \vec{v} | \;\; = \;\; \sqrt{v_x^2 + v_y^2 + v_z^2 } \end{array}[/math]
Wektor prędkości chwilowej jest zawsze styczny do toru!
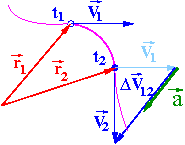
Przyspieszenie średnie
W odstępie czasu [math]\Delta t_{12} = t_2 - t_1 [/math] prędkość zmienia się o:
[math]\Delta \vec{V}_{12} = \vec{V}_2 - \vec{V}_1 = \vec{V}(t_2) - \vec{V}(t_1)[/math]
Przyspieszenie średnie definiujemy (podobnie jak prędkość średnią) jako stosunek przyrostu prędkości do odstępu czasu:
[math] \vec{a}^{^\textrm{(śr)}}_{12} = \frac{\Delta \vec{V}_{12}}{\Delta t_{12}}[/math]
Przyspieszenie chwilowe
Podobnie jak w przypadku prędkości, przyspieszenie chwilowe definiujemy jako graniczną wartość przyspieszenia średniego dla nieskończenie krótkiego przedziału czasu:
[math]\begin{array}{rcl} \vec{a} & = & \lim_{\Delta t \rightarrow 0}\; \frac{\Delta \vec{V}}{\Delta t} \;\; = \;\; \frac{d \vec{V}}{d t} \;\; = \;\; \dot{\vec{V}}\end{array}[/math]
Przyspieszenie chwilowe jest pochodną po czasie prędkości chwilowej:
[math]\begin{array}{rcl} \vec{a} = \frac{d \vec{V}}{d t} \!\! & = & \!\! \frac{d V_x}{d t}\cdot \vec{i}_x + \frac{d V_y}{d t}\cdot \vec{i}_y + \frac{d V_z}{d t}\cdot \vec{i}_z \\ & = & a_x \cdot \vec{i}_x + a_y \cdot \vec{i}_y + a_z \cdot \vec{i}_z \end{array}[/math]
Przyspieszenie opisuje "tempo" zmian prędkości…
Klasyfikacja ruchów
Ze względu na tor
Tor ruchu ciała może zakreślać dowolną krzywą w przestrzeni. W wielu zagadnieniach mamy jednak do czynienia z torem, który jest dodatkowo ograniczony przez symetrię zagadnienia lub warunki początkowe. Najchętniej zajmujemy się właśnie takimi przypadkami. W szczególności tor może być:
- prostoliniowy, odbywający się wzdłuż lini prostej
Zawsze możemy tak wybrać układ współrzędnych aby
- [math]\begin{array}{rcl} y(t) = z(t) = 0 & \Rightarrow & \vec{r}(t) = \vec{i}_x \cdot x(t) \end{array}[/math]
- płaski, odbywający się w ustalonej płaszczyźnie
Możemy tak wybrać układ współrzędnych aby
- [math]\begin{array}{rcl} z(t) = 0 & \Rightarrow & \vec{r}(t) = \vec{i}_x \cdot x(t) \; + \; \vec{i}_y \cdot y(t)\end{array}[/math]
- po okręgu
Ze względu na przyspieszenie
- jednostajny
- ⇒ wartość prędkości pozostaje stała: [math]| \vec{V} |[/math] = const
- jednostajnie przyspieszony
- ⇒ przyspieszenie jest stałe: [math] \vec{a} [/math] = const
Ruch jednostajny prostoliniowy
Najprostszy możliwy przypadek ruchu:
| * Jednostajny: [math]| \vec{V} |[/math] = const | [math]\left. ^{^{^{^{\;}}}} \right\} \;\; \Leftrightarrow \;\; \vec{a}\; = \;0 [/math] |
| * Prostoliniowy: [math]\frac{\vec{V}}{V}[/math] = const |
Wektor prędkości jest stały (nie zmienia wartości ani kierunku) czyli nie ma przyspieszenia.
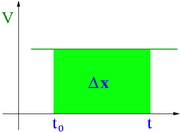
Przyjmując, że ruch odbywa się wzdłuż osi X:
[math]\begin{array}{rcl} V = \frac{dx}{dt} & = & const \\ & \Rightarrow & x = x_0 + V \cdot ( t - t_0 ) \;\;\;\;\;\;\;\; x_0 = x(t_0) \end{array}[/math]
Położenie (przebyta droga) jest liniową funkcją czasu.
Drogi przebyte w równych odcinkach czasu są sobie równe.
Ruch prostoliniowy
Zależność drogi od prędkości
Przypadek ogólny ruchu prostoliniowego:
- znamy prędkość [math]V(t)[/math]
- czy możemy wyznaczyć zależność położenia od czasu ?
Możemy sumować przesunięcia [math]dx[/math] po krótkich przedziałach czasu [math]dt[/math].
Przesunięcie ciała w czasie [math]\Delta t = t - t_0[/math]:
[math]\begin{array}{rcl} \Delta x & = & \sum_{dt} dx \; = \; \sum_{dt} V dt \end{array}[/math]
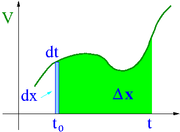
Przechodząc do granicy [math]dt \rightarrow 0[/math]:
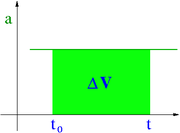
[math]\begin{array}{rcl} \Delta x & = & \int\limits_{t_0}^{t} V \; dt \end{array}[/math]
Zależność położenia od czasu wyraża się przez całkę oznaczoną. Pojęcie całki oznaczonej ma bardzo prostą interpretację graficzną: jest to pole pod krzywą zależności prędkości od czasu.
Ruch jednostajnie przyspieszony
Jednostajnie przyspieszony zdefiniowany jest poprzez warunek: [math] \vec{a} [/math] = const
Przyspieszenie opisuje zależność prędkości od czasu. Jeśli przyspieszenie jest stałe to prędkość musi rosnąć liniowo z czasem:
[math]\begin{array}{rcl} \vec{a} = \frac{d\vec{V}}{dt} & \Rightarrow & d\vec{V} = \vec{a} \; dt \\ & \Rightarrow & \vec{V} = \vec{V}_0 + \int\limits_{t_0}^{t} \vec{a}\; dt \\[3mm] & & \vec{V} = \vec{V}_0 + \vec{a} \cdot ( t - t_0 ) \;\;\;\;\;\;\;\;\;\;\;\; \vec{V}_0 = \vec{V}(t_0) \end{array}[/math]
Ruch jednostajnie przyspieszony prostoliniowy
Jaki warunek musi być spełniony, żeby ruch jednostajnie przyspieszony był prostoliniowy?
Ruch jest prostoliniowy wtedy gdy kierunek prędkości jest stały:
| [math]\frac{\vec{V}}{V}[/math] = const | [math]\Leftrightarrow[/math] | [math] \vec{V}\; || \;\vec{a}[/math] = const |
Aby ruch był prostoliniowy przyspieszenie musi mieć kierunek zgodny z kierunkiem prędkości.
Ruch prostoliniowy można opisać jako ruch jednowymiarowy wybierając oś układu odniesienia wzdłuż kierunku ruchu
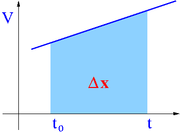
Prędkość jest liniową funkcją czasu:
[math]\begin{array}{rcl} V & = & V_0 + \int\limits_{t_0}^{t} a\; dt \;\; = \;\; V_0 + a \cdot ( t - t_0 ) \end{array}[/math]
Położenie jest kwadratową funkcją czasu:
[math]\begin{array}{rcl} x & = & x_0 + \int\limits_{t_0}^{t} V\; dt \;\; = \;\; x_0 + \int\limits_{t_0}^{t} \left[V_0 + a \cdot ( t - t_0 )\right] \; dt \\[5mm] & = & x_0 + V_0 \cdot ( t - t_0 ) + \frac{1}{2} \; a \cdot ( t - t_0 )^2 \\[3mm] & = & x_0 + \frac{1}{2}(V + V_0) \cdot ( t - t_0 ) \end{array}[/math]
Przyjmijmy, że w chwili [math]t_0=0[/math] ciało spoczywa:
- [math]V_0 = V(t_0) = 0[/math].
Mierzymy drogę jaką ciało przebywa w równych przedziałach czasu:
- [math]\begin{array}{rcl}\Delta t_n & = & t_n - t_{n-1} \;\; = \;\; \Delta t \\[3mm] & \Rightarrow & t_n \;\; = \;\; n \cdot \Delta t \end{array}[/math]
Przebyta droga:
- [math]\begin{array}{rcl} x(t) & = & \frac{1}{2} \; a \cdot t^2 \\[3mm] \Delta x_n & = & x(t_n) - x(t_{n-1}) \;\; = \;\; \frac{1}{2} \; a \cdot \left( t_n^2 - t_{n-1}^2 \right) \\[3mm] & = & \frac{1}{2} \; a \cdot \Delta t^2 \left( n^2 - (n-1)^2 \right) \;\; = \;\; \frac{1}{2} \; a \cdot \Delta t^2 \cdot (2n -1 )\end{array}[/math]
Uzyskujemy uniwersalną relację opisującą ruch jednostajnie przyspieszony prostoliniowy:
- Drogi w kolejnych odcinkach czasu mają się do siebie jak kolejne liczby nieparzyste:
- [math]\begin{array}{rcl}x_1 : x_2 : x_3 : \ldots & = & 1 : 3 : 5 : 7 : \ldots \end{array}[/math]
Przypadek ogólny
W ogólnym przypadku ruch jednostajnie przyspieszony nie jest prostoliniowy.
[math]\begin{array}{rcl} \vec{V} & = & \vec{V}_0 + \vec{a} \cdot ( t - t_0 ) \\ \vec{r} & = & \vec{r}_0 + \vec{V}_0 \cdot ( t - t_0 ) + \frac{1}{2} \; \vec{a} \cdot ( t - t_0 )^2 \end{array}[/math]
Ruch będzie się odbywał w płaszczyźnie przechodzącej przez [math]\vec{r}_0[/math] i wyznaczonej przez kierunki wektorów [math]\vec{V}_0[/math] i [math]\vec{a}[/math].
Możemy wybrać układ współrzędnych tak aby: [math]\begin{array}{rcl} \vec{i}_x \perp \vec{a} & \textrm{ ~~~oraz~~~} & \vec{i}_y \; || \; \vec{a} \end{array}[/math]
Ruch w przestrzeni można wtedy opisać jako złożenie:
- ruch jednostajnego (w kierunku osi X)
- ruchu jednostajnie przyspieszonego (Y)
- spoczynku (Z):
Formalnie możemy zapisać zależności współrzędnych przyspieszenia, prędkości i położenia od czasu jako:
| [math]\left\{\begin{array}{rcl} a_x & = & 0 \\ a_y & = & a \\ a_z & = & 0 \end{array}\right.[/math] | [math]\Leftrightarrow[/math] | [math]\left\{\begin{array}{rcl} V_x & = & V_{x,0} = const \\ V_y & = & V_{y,0} + a \; t \\ V_z & = & 0 \end{array}\right.[/math] | [math]\Leftrightarrow[/math] | [math]\left\{\begin{array}{rcl} x & = & x_0 + V_{x,0} \cdot (t-t_0) \\ y & = & y_0 + V_{y,0} \cdot (t-t_0) + \frac{1}{2} \; a\cdot ( t - t_0 )^2 \\ z & = & 0 \end{array}\right.[/math] |
Ruch w polu grawitacyjnym
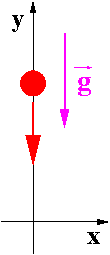
Ruch ciała poruszającego się swobodnie w jednorodnym polu grawitacyjnym odbywa się ze stałym przyspieszeniem:
[math]\begin{array}{rcl} \vec{a} & = & \vec{g} \;\; = \;\; (0, -g, 0) \end{array}[/math]
gdzie dokonaliśmy wyboru układu współrzędnych jak na rysunku (oś X poziomo, oś Y pionowo).
Pole grawitacyjne Ziemi możemy przyjąć za jednorodne, jeśli badamy ruch na odległościach [math]|\Delta \vec{r} | \ll R_Z[/math]
W zależności od warunków początkowych wyróżniamy następujące rodzaje ruchu:
- spadek swobodny: [math]V_0 = 0[/math] (ruch prostoliniowy)
- rzut pionowy: [math]\theta = \pm \pi/2[/math] (ruch prostoliniowy)
- rzut poziomy: [math]\theta = 0[/math]
- rzut ukośny: [math]\theta \ne 0, \pi/2, ...[/math]
Spadek swobodny
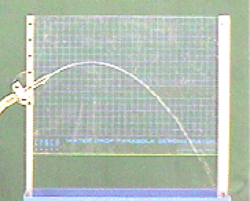
Zdjęcie złożone z kolejnych klatek filmu, pokazujące spadek swobodny małej piłki na tle miarki:
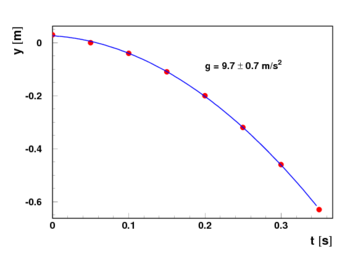
Wyniki "domowych" pomiarów (odczytane ze zdjęcia):
Położenie zależy kwadratowo od czasu:
[math]\begin{array}{rcl} y & = & h - \frac{g}{2} \cdot t^2 \end{array}[/math]
zakładając: [math]y(0)=h, \; V_{y}(0) = 0[/math]
Rzut ukośny
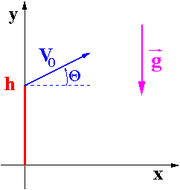
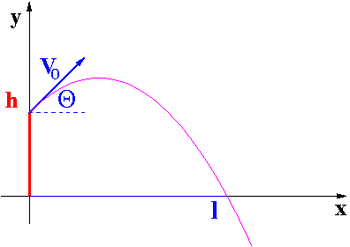
Zakładamy, ze w chwili [math]t_0 = 0[/math] ciało wyrzucono z punktu [math]x_0 = 0[/math], [math]y_0 = h[/math] z prędkością [math]V_0[/math] skierowaną pod kątem [math]\Theta[/math] do poziomu.
Niezależność ruchów:
- ruch w poziomie jest ruchem jednostajnym, zależy tylko od [math]V_{x,0}[/math]
- [math]\begin{array}{rcl} x & = & V_{x,0} \cdot t \;\; = \;\; V_0 \cos{\theta} \cdot t \end{array}[/math]
- ruch w pionie jest ruchem jednostajnie przyspieszonym, zależy tylko od [math]V_{y,0}[/math]
- [math]\begin{array}{rcl} y & = & h + V_{y,0} \cdot t - \frac{g}{2} \cdot t^2 \\ & = & h + V_0 \sin{\theta} \cdot t - \frac{g}{2} \cdot t^2\end{array}[/math]
Konsekwencje niezależności ruchów w X i Y:
- rzut poziomy [math]\theta = 0[/math] ⇒ [math]V_{y,0}[/math]
- ⇒ czas spadania nie zależy od [math]V_0[/math]: [math]t=\sqrt{\frac{2h}{g}}[/math]
- dwa ciała o tym samym [math]V^{(1)}_{x,0}=V^{(2)}_{x,0}[/math]
- ⇒ taki sam ruch w poziomie: [math]x^{^{(1)}}(t)=x^{^{(2)}}(t)[/math]
Tor w rzucie ukośnym:
- [math]\displaystyle y = h + x \cdot \tan{\theta} - x^2 \cdot \frac{g}{2 V_0^2 \cos^2 \theta } [/math]
- [math]\Rightarrow[/math] torem ruchu jest parabola
Zasięg dla h=0:
- [math] \displaystyle l = \frac{V_0^2}{g} \sin (2 \theta) [/math]
[math]\Rightarrow[/math] największy zasięg dla [math]\displaystyle \theta = \frac{\pi}{4}[/math] (czyli [math]45^\circ[/math])
Ruch harmoniczny
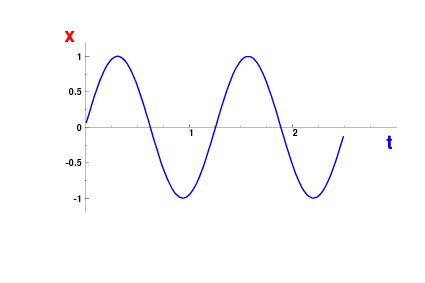
Szczególny przykład ruchu drgającego. W ruchu harmonicznym zależność położenia od czasu jest postaci:
- [math]\begin{array}{rcl} x & = & A \cdot \sin ( \omega t + \phi ) \end{array}[/math]
Parametry
- amplituda A
- częstość kołowa [math]\omega[/math]
- okres drgań [math]\displaystyle T=\frac{2 \pi}{\omega}[/math]
- faza początkowa [math]\phi[/math]
Prędkość:
- [math]\displaystyle V = \frac{dx}{dt} = \omega \; A \cdot \cos ( \omega t + \phi ) [/math]
Przyspieszenie:
- [math]\displaystyle a = \frac{dV}{dt} = -\omega^2 \; A \cdot \sin ( \omega t + \phi ) = -\omega^2 \cdot x [/math]
W ruchu harmonicznym spełniona jest zależność, którą nazywamy równaniem oscylatora harmonicznego
- ruch w jednym wymiarze
- [math] \frac{d^2 x}{dt^2} \; = \; - \omega^2 \; x [/math]
- postać ogólna
- [math] \frac{d^2 \vec{r}}{dt^2} \; = \; - \omega^2 \; \vec{r} [/math]
Równanie oscylatora dobrze opisuje zachowanie bardzo wielu układów fizycznych:
- ciężarek na sprężynie
- wahadło matematyczne (dla małych wychyleń)
- kamerton, struna, itp…
Równanie oscylatora harmonicznego jest przykładem równania różniczkowego.
Nasza wiedza nt. ruchu ciała przedstawiana jest często w postaci równan różniczkowych (równań ruchu). Aby znaleźć opis ruchu ciała trzeba te równania rozwiązać.
Najczęsciej są to równania typu: [math]\vec{a} = F(\vec{x},\vec{v},t)[/math]
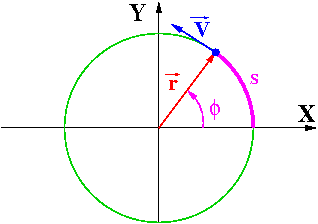
Ruch po okręgu
Położenie ciała może być opisane jedną zmienną:
- kąt w płaszczyźnie XY — [math]\phi[/math]
- długość łuku okręgu — s = [math]r \cdot \phi[/math]
Wartość prędkości:
- [math]\begin{array}{rcl} V & = & \frac{ds}{dt} \;\; = \;\; r \; \frac{d\phi}{dt} \;\; = \;\; r \; \omega \end{array}[/math]
gdzie prędkość kątowa jest zdefiniowana jako pochodna kąta [math]\phi[/math] po czasie:
- [math]\omega = \frac{d\phi}{dt}[/math]
Przyspieszenie kątowe definiujemy jako:
- [math]\displaystyle \alpha = \frac{d\omega}{dt} \;\; = \;\; \frac{d^2\phi}{dt^2}[/math]
Ruch jednostajny po okręgu to ruch w którym przyspieszenie kątowe znika:
| [math]\alpha = 0[/math] | [math]\Rightarrow[/math] | [math]\omega[/math] = const | [math]\Rightarrow[/math] | V = const |
| ale | [math]\vec{V} \ne [/math] const | |||
| [math]\vec{a} \ne[/math] 0 (!!!) |
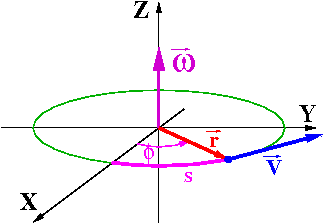
Prędkość w ruchu po okręgu w zapisie wektorowym:
- [math] \vec{V} = \vec{\omega} \times \vec{r}[/math]
Przyspieszenie liczymy jako pochodną (iloczynu):
- [math]\begin{array}{rcl} \vec{a} \;\; = \;\; \frac{d\vec{V}}{dt} & = & \frac{d\vec{\omega}}{dt}\times \vec{r} \; + \vec{\omega} \times \frac{d\vec{r}}{dt} \\[5mm] & = & \;\; \vec{\alpha}\times \vec{r} \; + \vec{\omega} \times \vec{V} \\[5mm] & = & \;\;\;\;\; \vec{a_t} \;\;\; + \;\;\; \vec{a_n} \end{array}[/math]
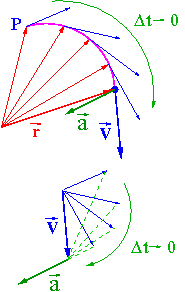
Oprócz przyspieszenia stycznego
[math]\vec{a_t} \uparrow \!\! \uparrow \vec{V}[/math],
opisującego zmianę [math]|\vec{V}|[/math],
jest też przyspieszenie normalne [math]\vec{a_n}[/math], odpowiedzialne za
zmianę kierunku [math]\vec{V}[/math] w czasie.
- przyspieszenie dośrodkowe
[math]\begin{array}{rcl} \vec{a_n} \;\; = \;\; \vec{\omega} \times \vec{V}
& = & \vec{\omega} \times ( \vec{\omega} \times \vec{r} )
\;\; = \;\; - \omega^2 \cdot \vec{r}
\end{array}[/math]
gdzie skorzystaliśmy z tożsamości:
- [math] A\times ( B \times C ) = (A\cdot C)\cdot B - (A\cdot B) \cdot C [/math]
Ruch jednostajny po okręgu
Ruch jednostajny po okręgu to ruch w którym przyspieszenie styczne znika: [math]\vec{a_t} = 0 [/math]
- [math]\begin{array}{rcl} \Rightarrow \qquad \vec{a} \; = \; \vec{a_n} & = & - \omega^2 \cdot \vec{r} \end{array}[/math]
Ruch jednostajny po okręgu jest złożeniem dwóch niezależnych ruchów harmionicznych:
- [math]\begin{array}{rcl} x & = & r \cdot \cos ( \omega \cdot t ) \;\; = \;\; r \cdot \sin ( \omega \cdot t + \frac{\pi}{2}) \\ y & = & r \cdot \sin ( \omega \cdot t ) \end{array}[/math]
| Ruch po okręgu | [math]\Longleftrightarrow[/math] | różnica faz [math]\Delta \phi = \pm \frac{\pi}{2}[/math] |
Ciekawostka:
Ruch harmoniczny można przedstawić jako złożenie dwóch ruchów po okręgu…
Efekt Dopplera
W przypadku fal dźwiękowych znamy z codziennego doświadczenia…
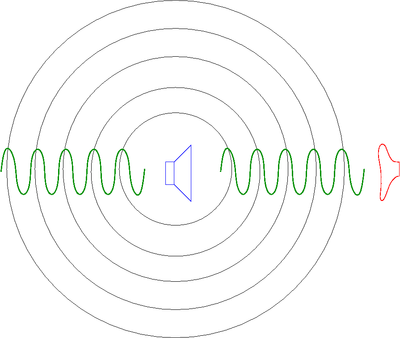
Jeśli źródło dźwięku jest nieruchome względem obserwatora, obserwator słyszy dźwięk o niezmienionej częstości.
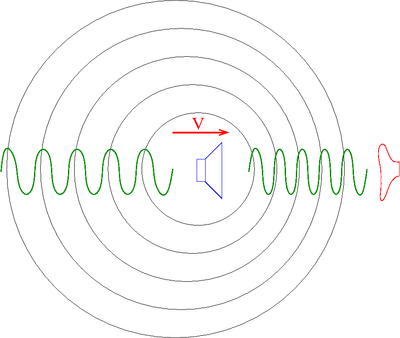
Jeśli źródło dźwięku porusza się względem obserwatora, obserwator słyszy dźwięk o wyższej lub niższej częstości
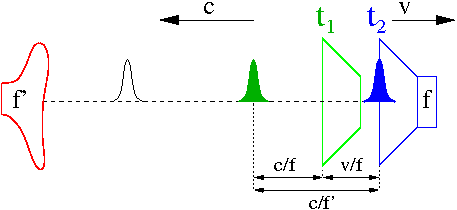
Ruchome źródło
Przyjmijmy, że źródło dżwięku o częstości [math]f[/math]
poruszające się z prędkością [math]v[/math]
względem ośrodka w którym prędkość dźwięku wynosi [math]c[/math].
Dla uproszczenia: krótkie impulsy wysyłane co [math]\Delta t = 1/f[/math]:
- [math]t_1[/math] — wysłanie pierwszego impulsu
- [math]t_2[/math] — wysłanie drugiego impulsu
odległość między impulsami mierzona przez obserwatora jest sumą wkładów wynikających z propagacji impulsu (z prędkością c) i ruchu źródła (z prędkością v):
- [math]\frac{c}{f'} = \lambda' = \frac{c}{f} + \frac{v}{f} [/math]
Częstość dźwięku i długość fali
mierzona przez obserwatora nieruchomego względem ośrodka:
| [math] f' = \frac{f}{1+\frac{v}{c}} [/math] | [math] \lambda ' = \lambda \; \left( 1+ \frac{v}{c}\right)[/math] |
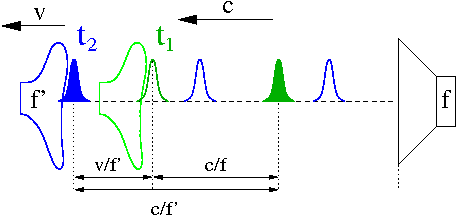
Ruchomy obserwator
Rozważmy teraz sytuacje, w której obserwator porusza się z prędkością [math]v[/math] względem ośrodka i źródła dżwięku
aby dogonić obserwatora kolejny impuls musi pokonać odległość równą sumie początkowej odległości między impulsami i drogi jaką w tym czasie pokona obserwator
- [math]\frac{c}{f'} = \frac{c}{f} + \frac{v}{f'} [/math]
Mierzona częstość:
- [math] f' = f \; \left(1-\frac{v}{c}\right) [/math]
W klasycznym efekcie Dopplera zmiana częstości zależy nie tylko
od względnej
prędkości źródła i obserwatora
ale i ruchu względem ośrodka.
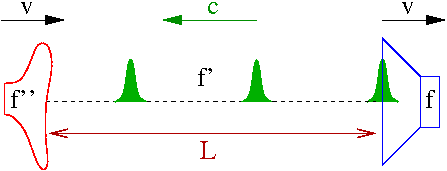
Ruch ośrodka
Przyjmijmy, że źródło dźwięku i obserwator są względem siebie w spoczynku. Niech ich prędkość względem ośrodka wynosi [math]v[/math]
Częstość mierzona przez obserwatora jest wynikiem złożenia dwóch efektów Dopplera:
[math]\begin{array}{rcl} f'' = f' \; \left(1+\frac{v}{c}\right) & = & \frac{f}{1+\frac{v}{c}} \cdot \left(1+\frac{v}{c}\right) = f \end{array}[/math]
Częstość się nie zmienia, ale zmienia się czas miedzy wysłaniem a rejestrają impulsu:
[math]\delta t = t''_i - t_i = \frac{L}{c+v} = \frac{L}{c} \cdot \frac{c}{c+v} = \frac{\delta t_0}{1+\frac{v}{c}} [/math]
Ruch ośrodka powoduje przesunięcie w fazie rejestrowanego dźwięku.
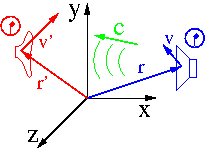
Przypadek ogólny
Zarówno źródło jak i obserwator poruszają się względem ośrodka.
Jeśli znamy ruch źródła i obserwatora w układzie związanym z ośrodkiem:
[math]\begin{array}{rcl} \vec{r}(t) & \;\;\; i \;\;\; & \vec{r}'(t) \end{array}[/math]
To możemy wyznaczyć czas [math]t'[/math] w jakim sygnał wyemitowany w chwili [math]t[/math] dotrze do obserwatora. Zadany jest on przez warunek:
[math]\begin{array}{rcl} \vec{r'}(t') - \vec{r}(t) = c \; ( t' - t ) \end{array}[/math]
Jeśli równanie to można jednoznacznie rozwiązać to efekt Dopplera daje się wyrazić bardzo prostą zależnością:
| [math]\frac{f'}{f} \; = \; \frac{~~\frac{1}{\Delta t'}~~}{\frac{1}{\Delta t}} \; = \; \frac{\Delta t}{\Delta t'}[/math] | [math]\Rightarrow[/math] | [math]f' \; = \; f \cdot \left( \frac{dt'}{dt} \right)^{-1}[/math] |
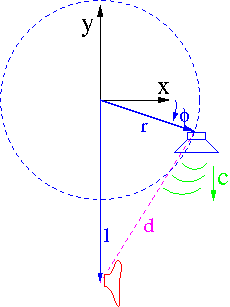
Przykład
- Głośnik wirujący po okręgu, w płaszczyźnie obserwatora
- [math]\begin{array}{rcl} \vec{x}(t) & = & r \cos \omega t \\ \vec{y}(t) & = & r \sin \omega t \\ x' & \equiv & 0 \\ y' & \equiv & -l \end{array}[/math]
Droga sygnału wyemitowanego w czasie [math]t[/math]:
- [math]\begin{array}{rcl} d = c \; ( t' - t ) & = & \sqrt{(l + r \sin \omega t)^2 \; + \; r^2 \cos^2 \omega t } \\[5mm] \Rightarrow \qquad t' & = & t + \frac{l}{c}\; \sqrt{1 + \frac{2r}{l} \sin \omega t \; + \; \frac{r^2}{l^2} } \end{array}[/math]
Dla [math]l \gg r[/math]:
[math]\begin{array}{rcl} t' \approx t + \frac{r}{c} \; \sin \omega t & \Rightarrow & f' \approx f \; ( 1 - \frac{r\omega}{c} \; \cos \omega t ) \end{array}[/math]
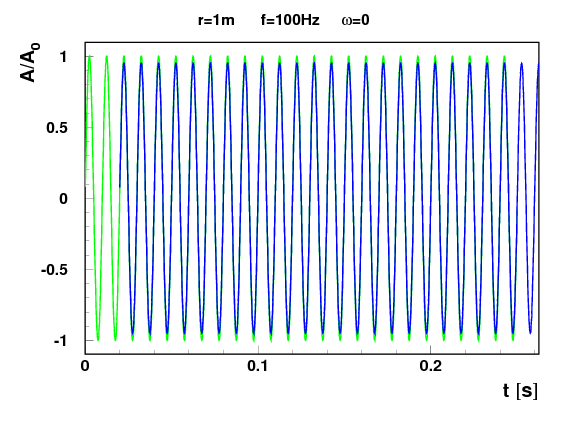
Oczekiwana zależność od czasu amplitudy dźwięku rejestrowanego przez źródło i obserwatora - Głośnik nieruchomy
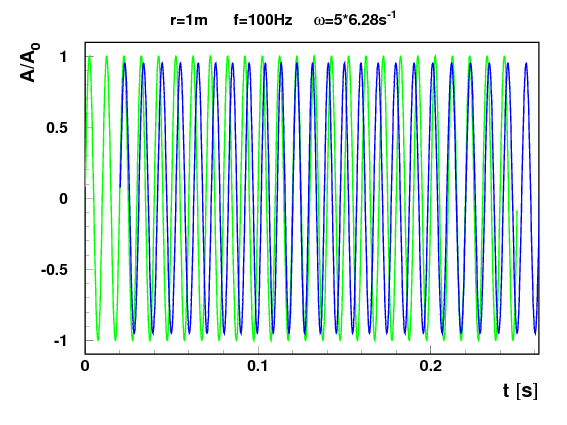
- Głośnik wirujący
- Choć średnia częstość mierzona przez obserwatora jest równa częstości źródła widoczna jest wyraźna modulacja częstości…