Elektrodynamika/Zadania domowe 1

1. Oblicz całkę krzywoliniową z funkcji

   [math]v=(r\cos^2\theta)\vec{e}_r-(r\cos\theta\sin\theta)\vec{e}_\theta +3r\vec{e}_\phi[/math]

   po zamkniętej krzywej składającej się kolejno z (współrzędne kartezjańskie):

   • prostej od punktu (0, 1, 0) do punktu (0, 1, 2);
   • prostej od punktu (0, 1, 2) do punktu (0, 0, 0);
   • prostej od punktu (0, 0 ,0) do punktu (1, 0, 0);
   • łuku okręgu o środku w (0, 0, 0) i promieniu 1 od punktu (1, 0, 0) do punktu (0, 1, 0).

   Zamienić tę całkę na całkę powierzchniową (zgodnie z odpowiednim twierdzeniem), obliczyć i porównać wyniki.

2. Oblicz całkę objętościową z funkcji

   [math]f(x,y,z)=y^2z[/math]

   po objętości stożka o czubku w punkcie (0, 0, 0) i podstawie w postaci koła o środku w punkcie (0, 0, 1) promieniu 1 (podstawa leży w płaszczyźnie z=1).

3. Znaleźć potencjał w całej przestrzeni pochodzący od dwóch równoległych cienkich nici naładowanych z gęstością liniową ładunku λ i −λ, odległych o a.
4. Oblicz pole elektryczne na osi cienkiego pręta o długości L (na zewnątrz pręta). Końce pręta są w punktach (0, 0, 0) i (0, 0, L), a pręt jest naładowany z gęstością liniową ładunku

   [math]\lambda(z)=z^2[/math].

5. Dany jest sześcian o boku a naładowany z gęstością objętościową ładunku

   [math]\rho(x,y,z)=\alpha x[/math].

   Układ współrzędnych jest umieszczony tak, że jeden z wierzchołków sześcianu jest w punkcie (0, 0, 0), a wychodzące z niego krawędzie pokrywają się z osiami układu w kierunku dodatnich współrzędnych. Znajdź moment dipolowy tego sześcianu. Czy konkretny wybór układu współrzędnych jest tutaj istotny?

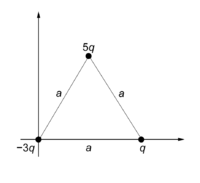
6. Oblicz elektryczne momenty multipolowe rzędu 0, 1 i 2 układu trzech ładunków umieszczonych w wierzchołkach trójkąta równobocznego o boku a, jak na rysunku.