
Elektroencefalografia/Biofizyczne podstawy generacji sygnałów EEG
W rozdziale tym poznamy mechanizmy neuronalne odpowiedzialne za powstawanie potencjałów na czaszce, mierzonych jako sygnały EEG. Rozdział ten jest opracowany w oparciu o Nunez (1981, 1995, 2006).
Spis treści
Własności tkanki nerwowej
Na początku zajmijmy się własnościami tkanki nerwowej, w której generowane są potencjały. Tkanka nerwowa składa się neuronów przekazujących impulsy nerwowe oraz komórek glejowych wspomagających działanie neuronów. W komórkach występuje płyn wewnątrzkomórkowy, a na zewnątrz, płyn zewnątrzkomórkowy. Płyn zewnątrz- i wewnątrzkomórkowy składa się z wody, białek oraz dodatnio i ujemnie naładowanych jonów. W płynie wewnątrzkomórkowym dominują jony K+, Mg2+, Na+, HCO3–, izetionianu. W płynie zewnątrzkomórkowym głównym kationem są jony Na+, a anionem jony Cl–. Ze względu na występowanie jonów swobodnych, w tkance nerwowej mogą płynąć prądy jonowe, w których biorą udział zarówno dodatnie, jak i ujemne jony. W odróżnieniu od obwodów elektrycznych, w których prąd jest rozłożony równomiernie w całym przekroju poprzecznym elementów obwodu i można operować pojęciem prądu całkowitego, w tkance nerwowej wygodnie operuje się uogólnionym pojęciem tzw. gęstością prądu J. Gęstość prądu pochodzącego do wielu różnych jonów, można wyrazić jako sumę poszczególnych przyczynków od jonów mających gęstość ładunku ρi i prędkość vi:
Gęstość ładunku jest równa wartości ładunku danego jonu pomnożonej przez liczbę wolnych jonów w elemencie objętości tkanki. Jednostką gęstości ładunku jest C/m3. vi są to średnie prędkości jonów wyrażone w metrach na sekundę. Gęstość prądu jest to ilość prądu przepływająca przez jednostkowy przekrój poprzeczny, a jego jednostką jest C/(m2s) lub A/m2. W skali makroskopowej (np. w próbce materii zawierającej 1020 lub więcej ładunków w ruchu), tkanka nerwowa spełnia prawo Ohma. Oznacza to liniową zależność pomiędzy gęstością prądu, a przyłożonym polem elektrycznym (E):
Stała proporcjonalności σ jest nazywana przewodnictwem elektrycznym ośrodka i wyraża się w jednostkach 1/(Ωm) lub równoważnie w Siemens/m (S/m). W tkance biologicznej często wygodniej jest stosować jednostki 1/(Ωcm) lub 1/(Ωmm) i (S/mm) Oporność jest odwrotnością przewodnictwa i jest mierzona w Ωm. Tkanka mózgowa jest słabym przewodnikiem. Np. makroskopowa oporność kory mózgowej jest ok. milion razy większa od oporności miedzi. Na poziomie mikroskopowym, błony komórkowe wykazują zachowanie nieliniowe, odbiegające od prawa Ohma. Gdy potencjał błonowy (pole elektryczne wewnątrz komórki) wzrasta powyżej pewnej wartości progowej, błona staje nieliniowym przewodnikiem, co umożliwia generacje i propagacje impulsów nerwowych.
Ładunki w przewodnikach
Wykonajmy myślowy eksperyment polegający na umieszczeniu ładunku próbnego w przewodniku np. tkance biologicznej. Gdy umieścimy dodatnio naładowany ładunek w przewodniku, występują dwa oddzielne efekty. Efekt polaryzacji spowodowany reorganizacją ładunków w błonach komórkowych (własności dielektryczne tkanki) oraz efekt przewodnictwa spowodowany ruchem ładunków swobodnych w płynie zewnątrzkomórkowym. Ten drugi efekt spowoduje, że dodatni ładunek próbny będzie wkrótce otoczony chmurą ujemnych ładunków, które będą w dużym stopniu ekranować pole pochodzące od ładunku próbnego. Potencjał w punkcie r, pochodzący od ładunku próbnego umieszczonego w elektrolicie w punkcie r1 był wyprowadzony w połowie XX wieku na bazie rozważań statystycznych i wynosi:
RD jest tzw. długością Debye'a, a κ odpowiada za efekty polaryzacyjne. R = |r – r1|. Dla κ = 1 i R ≪ RD, dostajemy potencjał ładunku punktowego w próżni. Jednakże RD jest rzędu kilku angstremów (10–10 m) w tkance biologicznej, co powoduje, ze eksponent we wzorze (Equation 3) wynosi ok. 10–4000000 w odległości R = 3 mm. Pokazuje to, że potencjał ładunku próbnego umieszczonego w tkance biologicznej jest zaniedbywalnie mały dla wszystkich makroskopowych odległości. Nie można więc powiedzieć, że potencjały w mózgu są spowodowane pewnym rozkładem określonym ładunku. Są one spowodowane nie tylko określonym rozkładem ładunku ale również wszystkimi ładunkami w ośrodku przewodzącym. W tkance biologicznej, źródła prądowe w błonach neuronalnych, a nie ładunki, są generatorami EEG.
Podstawowe równania
Wszystkie zjawiska elektryczne i magnetyczne w mózgu podlegają uniwersalnym prawom Maxwella:
gdzie D — indukcja elektryczna , E — natężenie pola elektrycznego, B — indukcja magnetyczna, H — natężenie pola magnetycznego, ρ — gęstość ładunku, J — gęstość prądu. W wielu materiałach, również w tkance nerwowej, pola D i B zależą liniowo od E i H:
Gdzie: ε — przenikalność elektryczna, a μ — przenikalność magnetyczna ośrodka.
Do opisu pól elektrycznych w tkance nerwowej stosuje się uproszczoną wersje równań Maxwella oraz równań opisujących liniowe własności ośrodka. Podstawowe równania liniowej elektrofizjologii można podsumować następująco:
Zasada zachowania ładunku (równanie %i 10) wynika bezpośrednio z 1 i 4 równania Maxwella (równania %i 4 i %i 7), oraz z tożsamości
Równanie potencjału skalarnego dla pola elektrycznego (równanie %i 14) jest spełnione w przybliżeniu wolnych oscylacji pól, co pozwala zaniedbać indukcję magnetyczną.
Warunki brzegowe w ośrodkach niejednorodnych
Różne obszary mózgu mają różne przewodnictwa, tak więc w praktycznych zagadnieniach występują granice między ośrodkami. W skali makroskopowej, najbardziej oczywiste granice między ośrodkami dotyczą granicy pomiędzy słabo przewodzącą czaszką i powietrzem otaczającym głowę. W skali mikroskopowej mamy do czynienia z granicami tworzonymi przez błonę komórkową z ośrodkiem zarówno zewnętrznym jak i wewnętrznym. Potencjał elektryczny Φ(r, t) będzie miał różne rozwiązania Φi(r, t) w obszarach i o przewodnictwie σi. Porównajmy najpierw efekty opornościowe i efekty pojemnościowe. Zastosujmy operator ∇ do czwartego równania Maxwella (równanie %i 7) oraz skorzystajmy z tożsamości (Equation 15). Dostajemy:
Rozważmy składową pola elektrycznego oscylującego z częstością f
i wyraźmy równanie (Equation 16) stosując prawo Ohma (Equation 12) i liniowe równanie dla dielektryka (Equation 13):
Dwa wyrażenia w nawiasie odpowiadają za efekty opornościowe i pojemnościowe w ośrodku materialnym, tzn. efekty związane z ładunkiem swobodnym i efekty związane z ładunkami związanymi w błonie komórkowej. Oznacza to, że efekty pojemnościowe możemy zaniedbać gdy
Gdy w obszarze i oraz j nie występują źródła, na mocy równania (Equation 16) i równania potencjału skalarnego (równanie Equation 14), podstawowe równania elektrofizjologii redukują się do:
równanie (Equation 20) odnosi się do sytuacji, w której można zaniedbać efekty pojemnościowe (np. błony komórkowej) i nosi nazwę równania Laplace’a. Czasem przybliżenie to nazywa się również przybliżeniem quasi-statycznym, gdyż stosuje się dla pól oscylujących z niskim częstościami. Równanie to stosuje się do wszystkich zagadnień w skali makroskopowej. Równanie (Equation 21) stosuje się do błon komórkowych i pól w skali mikro. Równania (Equation 20) i (Equation 21) mają nieskończenie wiele rozwiązań. Aby rozwiązanie w każdym obszarze było jednoznaczne należy zastosować warunki brzegowe na granicy ośrodków oznaczonych symbolami m i n:
Warunki brzegowe są wyrażone we współrzędnej u, mającej wszędzie kierunek normalny do granicy między ośrodkami i dwóch współrzędnych stycznych w1 i w2. Pierwszy z warunków określa fizyczne wymaganie by składowa normalna gęstości prądu była ciągła na granicy ośrodków. Warunek ten wynika z zasady zachowania ładunku. Drugi warunek brzegowy określa, że składowa styczna pola elektrycznego musi być ciągła na granicy ośrodków. Warunek ten wynika z drugiego prawa Maxwella. Stosując pierwszy z warunków brzegowych do granicy głowa (m)–powietrze (n) i przyjmując, że przewodnictwo powietrza wynosi zero, dostajemy:
Oznacza to, że pole magnetyczne, elektryczne oraz ich potencjały pochodzące od źródeł w mózgu, rozchodzą się w przestrzeni otaczającej głowę, lecz prąd jest ograniczony do jej wnętrza (składowa normalna prądu wynosi zero).
Źródła prądowe w mózgu
Tzw. problem wprost w EEG polega na obliczeniu potencjału na czaszce na podstawie źródeł prądowych. Równania (Equation 20, Equation 21) w pełni opisują szukany potencjał jednakże potrzebna jest modyfikacja. Wersja niezmodyfikowana wymaga znajomości potencjału i jego pochodnych normalnych na granicy ośrodków, co jest skomplikowane w skali komórkowej. Ponieważ jednak składowa normalna potencjału jest proporcjonalna do gęstości prądu w przewodniku, możemy zastąpić warunki brzegowe na granicy ośrodków poprzez odpowiednie źródła prądowe. Na początku rozważmy prąd błonowy pojawiający się w wyniku aktywacji pojedynczej synapsy.
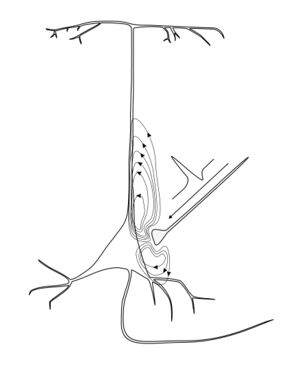
W stanie spoczynku, potencjał wewnątrz komórki wynosi ok. –65 mV względem potencjału na zewnątrz. Jeżeli synapsa jest pobudzająca, efektem jej aktywacji będzie zwiększenie przepuszczalności dla dodatnio naładowanych jonów, które zaczną napływać do komórki. Zmiana potencjału błonowego w wyniku akcji synaptycznej nazywana jest pobudzającym potencjałem postsynaptycznym lub EPSP (od ang. excitatory postsynaptic potential). EPSP zmniejsza wartość różnicy potencjału w komórce i podnosi jej wewnątrzkomórkowy potencjał w kierunku odpalenia jej własnego potencjału czynnościowego, przy różnicy potencjałów w poprzek błony ok. –40 mV. Błona w bezpośredniej okolicy synapsy zachowuje się jak zlew prądowy (źródło ujemne) gdyż dodatnio naładowane jony wpływają do wewnątrz. Prąd płynie w przestrzeni wewnątrzkomórkowej i wypływa z komórki w dalszych, rozproszonych obszarach, tak aby zamknąć linie prądu. Całkowity prąd dokomórkowy musi być równy całkowitemu prądowi wypływającemu z komórki, co wynika z zasady zachowania ładunku. Jeżeli synapsa jest hamująca, zmiana potencjału błonowego w wyniku akcji synaptycznej nazywana jest hamującym potencjałem postsynaptycznym lub IPSP (od ang. inhibitory postsynaptic potential). Ma on odwrotne działanie w stosunku do EPSP i zmniejsza prawdopodobieństwo generacji potencjału czynnościowego. IPSP generuje powstanie lokalnego źródła prądu, któremu musi towarzyszyć odpowiedni zlew prądowy rozproszony wzdłuż bardziej odległych obszarów błony (rys. 1). Potencjał zewnątrzkomórkowy powstający w wyniku akcji synaptycznej zależy od pełnego rozkładu źródeł i zlewów w błonie s(r, t), a nie tylko od lokalnego prądu płynącego w otoczeniu synapsy. W wyniku złożonej geometrii neuronów, geometria rozkładu prądów płynących przez błonę może być skomplikowana, a potencjał zewnątrzkomórkowy trudny do policzenia. Jednakże w zagadnieniach EEG, możemy obejść wiele problemów ze złożonością pojedynczych neuronów poprzez zmianę skali, w której rozpatrujemy generatory prądów. W tym celu zdefiniujmy efektywny prądowy moment dipolowy dla każdej objętości tkanki. Prądowy moment dipolowy na jednostkę objętości tkanki kory mózgowej może być uważany za korowe źródło generujące pole magnetyczne i elektryczne na powierzchni czaszki. Kluczem do zrozumienia tego upraszczającego założenia jest fakt, że pojedyncza komórka kory mózgowej dostaje ok. 104-105 wejść synaptycznych, a pod każdym milimetrem kwadratowym powierzchni kory znajduje się ok. 105 neuronów. Potencjał zewnątrzkomórkowy mierzony przez małą elektrodę z takiego obszaru będzie bardzo skomplikowany i będzie bardzo czuły na zmianę położenia elektrody. Jednakże w odległościach dużych w porównaniu z charakterystyczną odległością pomiędzy źródłami i zlewami, potencjał generowany przez źródła i zlewy w kolumnie będzie przypominał potencjał dipola. Dla wielu kolumn wykazujących aktywność synaptyczną, potencjał na czaszce będzie ważoną sumą dipolowych przyczynków od poszczególnych kolumn. W komórce piramidowej, charakterystyczna odległość pomiędzy źródłem a zlewem jest rzędu paru milimetrów, podczas gdy odległość do najbliższych obszarów na czaszce wynosi ok. 1-1,5 cm. Tak więc przybliżenie dipolowe dla źródeł w kolumnach korowych jest spełnione w zagadnieniach EEG.
Bezpośrednie zastosowanie makroskopowych źródeł prądu
We wszystkich następujących zagadnieniach będziemy zakładać, że ośrodek jest czysto przewodzący i nie wykazuje efektów pojemnościowych. W takim ośrodku, ładunek nie jest nigdzie gromadzony, gęstość ładunku jest stała, a równanie zachowania ładunku można zapisać:
Korzystne okazuje się wprowadzenie pojęcia makroskopowej gęstości prądu źródeł Js, która pozwala zapisać prawo Ohma następująco:
Oznacza to, że prąd całkowity w ośrodku przewodzącym składa się prądu omowego σE oraz prądu źródłowego wypływającego z granicy między ośrodkami np. prąd wypływający przez błonę komórkową. Wstawiając (Equation 26) do (Equation 25) i korzystając z definicji potencjału elektrycznego dostajemy:
gdzie objętościowy prąd źródłowy jest zdefiniowany jako
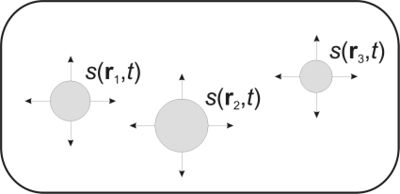
Przewodnictwo σ(r) (w S/mm lub S/cm) w ogólności zależy od położenia i dlatego znajduje się wewnątrz operatora ∇. Gęstość prądu źródłowego s(r, t) ma wymiar prądu na jednostkę objętości μA/mm2. Jest to prąd generowany w jednostce objętości. Może być również interpretowany jako objętościowe źródło potencjału generowanego w ośrodku makroskopowym. Rozumowanie stojące za wprowadzeniem prądu źródłowego jest następujące. Dowolny obszar tkanki możemy podzielić tak, że obszary generacji prądu znajdują się pewnych podobszarach oznaczonych kolorem szarym na rys. 2. W pozostałych obszarach (zaznaczonych kolorem białym) potencjał jest określony równaniem Laplace’a (Equation 20) w ośrodku jednorodnym i (Equation 27) w ośrodku niejednorodnym, kładąc s(r, t) równe zero. Jednakże jednoznaczne rozwiązanie wymaga by potencjał lub składowa normalna potencjału była określona na całej granicy ośrodków. W formalizmie równania Poissona (Equation 27) zastąpiliśmy warunki brzegowe poprzez prąd objętościowy s(r, t). Ujemny znak w równaniu (Equation 27) jest spójny z prądem dodatnim wpływającym do bezźródłowego (białego) obszaru. Inna zaletą tego podejścia jest fakt, że w ośrodku czysto przewodzącym czasowa zależność potencjału Φ(r, t) jest identyczna z czasową zależnością źródła. Pojedyncze oscylujące źródło s(r, t) ∼ sin(2πft) powoduje oscylacje potencjału z tą samą częstością. Jednakże w mózgu będzie zazwyczaj wiele źródeł oscylujących z różnymi częstościami i fazami. Potencjał na czaszce mierzony w EEG będzie liniową superpozycją przyczynków od pojedynczych obszarów źródeł z różnymi wagami zależnymi od własności przewodnictwa ośrodka i odległości pomiędzy źródłami i miejscami pomiaru potencjału na czaszce. Przeprowadzone tutaj operacje matematyczne mogą się wydawać nieco sztuczne, okazują się jednak bardzo wygodne w zrozumieniu problemów związanych z generacją potencjałów w tkance nerwowej. Porównajmy wzór na potencjał w przewodniku pochodzący od obszaru źródła prądowego s(r, t) (Equation 27) ze wzorem na potencjał w dielektryku pochodzący od obszaru źródła z pewną gęstością swobodnego ładunku ρ(r, t). Równanie na potencjał w dielektryku otrzymamy poprzez połączenie równań (Equation 4), (Equation 8) i (Equation 14). Prowadzi to do równania Poissona w dielektryku:
Oba równania (Equation 29) i (Equation 27) są równaniami Poissona lecz ze zmienionymi symbolami. Są one więc matematycznie równoważne lecz reprezentują inne fizycznie procesy. Swobodny ładunek makroskopowy w przewodniku w praktyce wynosi zero, tak więc równanie (Equation 29) nie ma praktycznego zastosowania w elektrofizjologii. Jednakże w fizyce znanych jest wiele rozwiązań równania (Equation 29) dla różnych rodzajów niejednorodności w dielektrykach. Aby zastosować znane z fizyki rozwiązania do przewodnika wystarczy w nich podstawić przewodnictwo σ(r, t) w miejsce przenikalności elektrycznej ε(r, t), a źródła ładunku ρ(r, t) zamienić na źródła prądowe s(r, t). Np. rozważmy specjalny przypadek N punktowych źródeł prądowych, co oznacza, że rozmiary (objętość) źródła jest dużo mniejsza niż odległość od elektrod pomiarowych. W nieskończonym, jednorodnym i czysto opornościowym przewodniku, potencjał na zewnątrz źródeł jest analogiczny do potencjału pochodzącego od N ładunków punktowych i wynosi:
W typowych jednostkach stosowanych w zagadnieniach EEG, In(t) są jednobiegunowymi źródłami prądowymi (μA) wypływającymi z n-tego rejonu źródła do przewodnika o przewodnictwie σ (1/(Ωcm)). Rn są odległościami pomiędzy miejscem pomiaru a położeniem źródła. Np. potencjał w odległości 1 cm generowany przez źródło prądowe o natężeniu 4π μA w wyidealizowanej korze mózgowej o oporności η = 1/σ = 300 Ωcm, wynosi 300 mV. W ośrodku czysto opornościowym, zależność czasowa potencjału jest dana przez sumę ważoną wszystkich źródeł. W ośrodku z własnościami pojemnościowymi wystąpią przesunięcia fazowe pomiędzy źródłami i potencjałem. Gdy zaniedbamy efekty pojemnościowe, otrzymamy ogólną metodę znajdowania potencjału na podstawie rozkładu źródeł prądowych w mózgu.
Źródła prądowe w ośrodku przewodzącym
Większość zjawisk obserwowanych w zapisie EEG może być zrozumiana na podstawie paru rodzajów źródeł. W szczególności jest to dipol prądowy, warstwa dipolowa i rozkład źródeł pochodzący od potencjału czynnościowego. Pole na czaszce, pochodzące od tych źródeł będzie oczywiście silnie zależeć od makroskopowych niejednorodności takich jak czaszka. My zajmiemy się uproszczoną sytuacją i rozważymy różne przykłady źródeł w nieskończonym, jednorodnym i izotropowym ośrodku przewodzącym. Przybliżenie to dostarczy nam ważnej intuicji na temat generatorów rzeczywistych sygnałów EEG.
Źródło jednobiegunowe
Potencjał pojedynczego źródła jednobiegunowego jest szczególnym przypadkiem rozwiązania (Equation 30) i wynosi
Równanie (Equation 31) można też otrzymać przeprowadzając proste rozumowanie. Otoczmy punktowe źródło sferą o promieniu r. Ponieważ prąd całkowity jest zachowany, gęstość prądu na powierzchni sfery wynosi
w kierunku radialnym. Z prawa Ohma:
Stosując równanie potencjału skalarnego (Equation 14), dla składowej radialnej dostajemy:
Po scałkowaniu (Equation 34) dostajemy równanie (Equation 31). Z równania (Equation 31) wynika, że potencjał w przewodniku staje się nieskończony jeśli odległość między źródłem a punktem pomiaru wynosi zero lub przewodnictwo ośrodka wynosi zero. Ta nie-fizyczna sytuacja wynika z dwóch założeń zrobionych przy wyprowadzaniu równania (Equation 31). Po pierwsze, założyliśmy, że pomiar dokonywany jest punktowo lecz prawdziwe elektrody pomiarowe mają niezerowe rozmiary więc r nie może być zero. Po drugie, założyliśmy, że jesteśmy w stanie zapewnić stałe natężenie prądu niezależnie od przewodnictwa ośrodka. Jednakże gdy przewodnictwa ośrodka będzie malało, coraz większe napięcie z generatora będzie wymagane, by utrzymać stały prąd w źródle. W rzeczywistości, gdy przewodnictwo ośrodka będzie dążyć do zera, natężenie prądu I będzie również dążyło do zera, co zapewni skończoną wartość potencjału.
Dipol prądowy
Dipol prądowy składa się z punktowego źródła I i zlewu –I, oddzielonych o d. Znaczenie dipola w elektrofizjologii jest większe niż jakakolwiek inna konfiguracja źródeł. Jest tak dlatego, że prawie każdy obszar zawierający źródło i zlew, oraz w którym całkowity prąd źródła i zlewu są równe (zasada zachowania prądu), będzie dawał przybliżone pole dipola w odległościach dużych w porównaniu z rozmiarami obszaru źródło-zlew. Np. pole dipola jest generowane w wyniku pobudzenia lub hamowania synaptycznego w neuronach, jak to zostało opisane w sekcji Źródła prądowe w mózgu. Ścisłe wyrażenie na potencjał dipola jest to suma dwóch jednobiegunowch przyczynków o przeciwnej polaryzacji i odległościach odpowiednio r1, r2 od punktu pomiaru:
Jednakże dużo wygodniej wyrazić potencjał dipola za pomocą jednej współrzędnej radialnej r, mierzonej od środka odcinka łączącego ładunki. W odległościach dużo większych od d, pole dipola można przybliżyć następująco:
dla r ≫ d. Θ jest kątem pomiędzy osią dipola i wektorem r wskazującym punkt pomiaru. Rozważmy lokalny przepływ prądu pomiędzy III i VI warstwą kory mózgowej. Odległość między biegunami prądu wynosi wtedy d ~ 1 mm. Załóżmy prądowe źródło o natężeniu I = 10 μA i nieskończony jednorodny ośrodek o oporności η = 1/σ = 300 Ωcm odpowiadającej korze mózgowej. Licząc potencjał (względem nieskończości) wzdłuż osi dipola (Θ = 0), możemy zastosować (Equation 36) również w pobliżu źródeł. Wstawiając dane dostajemy:
- Φ(r, 0) ≈ 464 μV dla r = 2,5 mm (na powierzchni kory)
- Φ(r, 0) ≈ 12 μV dla r = 1,5 cm (na czaszce)
Powyższe oszacowania nie biorą pod uwagę wpływu warstw płynu mózgowo-rdzeniowego, czaszki i skóry na głowie i powietrza nad głową. Szacuje się, że wpływ tych warstw o różnym przewodnictwie zmniejsza potencjał pochodzący od dipola znajdującego się w powierzchownych warstwach kory, a mierzonego na czaszce do ok. 1/4 wartości otrzymanej w jednorodnym modelu kory. Te zgrubne oszacowania pozwalają nam przewidzieć stosunek potencjału mierzonego na czaszce do potencjału mierzonego na powierzchni kory. Dla pojedynczego źródła korowego stosunek ten wynosi 464/(12/4), a więc:
- Potencjał na korze/potencjał na czaszce ~ 100 do 200
Średnie amplitudy spontanicznego EEG na korze są zazwyczaj 2 do 5 razy większe od potencjałów mierzonych na czaszce (Cooper et al., 1965). Brak zgodności naszego oszacowania z doświadczeniem sugeruje, że zdecydowana większość zjawisk w EEG jest generowana nie przez pojedyncze dipole lecz przez źródła o znacznie większych rozmiarach np. przez warstwy dipolowe. Z drugiej strony, niektóre iglice epileptyczne (ang. epileptic spikes) i potencjały wywołane (ang. evoked potentials) w pierwszorzędowej korze sensorycznej można z powodzeniem modelować jako pojedynczy dipol lub parę izolowanych dipoli.
Źródło kwadrupolowe
Rozróżniamy dwie konfiguracje prowadzące do źródła kwadrupolowego. Kwadrupol liniowy składa się z dwóch źródeł +I/2 i zlewu –I leżących wzdłuż jednej prostej, oddzielonych od siebie o d. Kwadrupol dwuwymiarowy składa się z dwóch identycznych dipoli, umieszczonych równolegle do siebie, o przeciwnej orientacji. Kwadrupol liniowy ma zastosowanie w elektrofizjologii gdyż wykazuje podobieństwo do trójfazowego rozkładu źródeł we włóknie nerwowym podczas potencjału czynnościowego. Potencjał kwadrupola w dowolnym miejscu ośrodka przewodzącego wynika bezpośrednio ze wzoru (Equation 31) na potencjał pojedynczego źródła jednobiegunowego
Trzy wartości r odpowiadają trzem odległościom pomiędzy źródłami i zlewami, a punktem pomiaru. W średnich lub dużych odległościach, potencjał może być wyrażony we współrzędnych sferycznych (r, θ, φ) jako
Potencjał nie zależy od współrzędnej φ.
Podczas generacji potencjału czynnościowego następuje wpływ dodatniego prądu jonów Na+ do wnętrza komórki. Prądowe źródło na pewnym obszarze błony komórkowej musi mieć odpowiadające mu zlewy prądowe, które znajdują się w obszarach po obu stronach źródła. W ten sposób powstaje konfiguracja źródło-zlew przypominająca kwadrupol liniowy. Ponieważ potencjał kwadrupola zanika jak 1/r3 czyli szybciej niż potencjał dipola (1/r2), potencjały czynnościowe mają znikomy wpływ na sygnał EEG. Synchronicznie występujące potencjały czynnościowe (ang. compound action potentials) mogą jednak być mierzalne. Istnieją podstawy by sądzić (Jewett, 1970), że potencjały czynnościowe biegnące we nerwie słuchowym są przynajmniej częściowo źródłem słuchowych potencjałów wywołanych z pnia mózgu (BAER od ang. brainstem auditory evoked response).
Warstwa dipolowa — najważniejsze źródło sygnału EEG
Około 65 do 75% neuronów korowych u wszystkich gatunków ssaków jest ustawionych prostopadle do powierzchni kory (Scholl, 1956; Bok, 1959). Neurony korowe mają dużą liczbę wzajemnych połączeń powodujących synchronizacje ich aktywności. Istnieją więc zarówno anatomiczne, jak i fizjologiczne podstawy by uznać warstwę dipolową tworzoną przez równoległe, synchronicznie działające komórki, za generator potencjałów korowych. Synchronizacja generatorów odgrywa tutaj kluczową rolę. Rozważmy na początku dwa dipole, których prądy fluktuują z częstościami [math]f_A[/math] i [math]f_B[/math]. Może to odpowiadać dwóm komórkom, dostającym zarówno wejścia pobudzające, jak i hamujące (rys. 3). Potencjał mierzony przez elektrodę w punkcie P, otrzymamy na podstawie (Equation 30):
IA oraz IB są maksymalnymi wartościami prądu w każdym z dipoli. Dodatkowo, zakładamy, że cały prąd wypływający ze źródła wpływa do zlewu w tym samym dipolu, co jest spełnione gdy odległość między dipolami Ljest znacznie większa niż odległość pomiędzy efektywnymi biegunami d. αA i [math]\alpha_B[/math] są kątami fazowymi. Dla większej ilości źródeł, w wyrażeniu (Equation 39) pojawią się analogiczne człony.
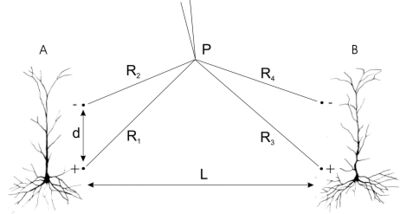
Rozważmy wpływ wielu dipoli o podobnej sile ([math]I_A = I_B = I_C[/math], itd) i podobnych częstościach ([math]f_A = f_B = f_C[/math], itd) na średni potencjał [math]|\bar{\Phi}|[/math]. Potencjał będzie oczywiście zależał od wszystkich odległości R1, R2, itd., możemy jednak sformułować pewne ogólne wnioski.
- a. Gdy generatory są ze sobą w fazie ([math]\alpha_A [/math] = [math]\alpha_B [/math] = [math]\alpha_C [/math] , itd), a dipole ustawione równolegle do siebie, wyrażenia we wzorze (Equation 39) dodają się i dla m dipoli, uśredniony po czasie potencjał będzie proporcjonalny do ilości wszystkich m generatorów w otoczeniu elektrody,
- [math] |\bar{\Phi}| \sim m[/math]
- Oczywiście, generatory znajdujące się najbliżej elektrody, będą miały największy wpływ na potencjał, lecz im więcej generatorów będzie aktywnych w losowych odległościach od punktu pomiaru, wzór (Equation 40) będzie stanowić tym lepsze przybliżenie.
- b. Jeśli generatory mają losową orientację, tak że prądy I w (Equation 39) będą miały losowe znaki lub jeśli losowe będą fazy generatorów, potencjał będzie dużo słabiej zależał od liczby generatorów. Będzie on wynikiem statycznej fluktuacji. Wg. Nunez (1981), można pokazać, że m członów w wyrażeniu (Equation 39) sumuje się dając średni potencjał, który dla dużych m można oszacować jako:
- [math] |\bar{\Phi}| \sim \sqrt{m}[/math]
Zastosujmy teraz powyższe rozważania do zapisu rejestrowanego elektrodą umieszczoną w pobliżu generatorów. Jeśli elektroda znajduje się wystarczająco blisko źródła prądowego, tak że jeden z Rs w (Equation 39) jest bardzo mały, mierzony potencjał będzie stosunkowo duży, bez względu na fazowe relacje pomiędzy źródłem lokalnym i innymi źródłami w otaczającej tkance. Źródła odległe również mogą dawać wkład do mierzonego potencjału. Ich wkład może być mniejszy lub większy od wkładu źródła lokalnego. Źródła odległe będą zachowywały się głównie jak dipole prądowe. Tak więc potencjał mierzony przez elektrodę może być wyrażony następującym przybliżonym wzorem.
Indeksy i, S, oraz A odnoszą się odpowiednio do źródeł lokalnych, źródeł odległych synchronicznych i źródeł odległych asynchronicznych. Is są prądami efektywnymi, które mogą być mniejsze niż prąd całkowity, w zależności od orientacji odległych synchronicznych źródeł względem elektrody. d jest odległością pomiędzy efektywnymi biegunami dipoli. l, m i n są liczbą źródeł lokalnych, odległych synchronicznych i odległych asynchronicznych, które znajdują się odpowiednio w średnich odległościach R[math]_{i}[/math], R[math]_S[/math], R[math]_A[/math]. Należy pamiętać, że (Equation 42) jest idealizacją, gdyż nie wszystkie generatory dają się zaklasyfikować do poszczególnych kategorii, jednakże wzór ten może dać ogólny pogląd na generacje potencjałów w mózgu, a w szczególności potencjałów mierzonych na czaszce czyli EEG. W tym przypadku (EEG) nie ma źródeł lokalnych. Jeśli generatory są podobne IS ≈ IA oraz generatory synchroniczne i asynchroniczne są w podobnej odległości RS ≈ RA, względny przyczynek od generatorów synchronicznych względem asynchronicznych wynosi:
Na podstawie zależności (Equation 43) możemy przeprowadzić następujące rozumowanie. Elektroda umieszczona na czaszce mierzy aktywność ok. 10[math]^8[/math] neuronów znajdujących się w paru cm[math]^2[/math] kory, Załóżmy, że prawie wszystkie neurony są aktywne lecz tylko 1% (10[math]^6[/math]) z nich jest ustawiony równolegle i działa synchronicznie. Przyczynek od synchronicznej frakcji neuronów do potencjału mierzonego na czaszce wynosi:
Jest on więc 100 razy większy niż przyczynek od pozostałych 99% neuronów (Elul, 1972). Pokazuje to, że powierzchniowe EEG pochodzi głównie od synchronicznej aktywności równolegle ustawionych neuronów, a zmiana amplitudy sygnału wraz ze stanem fizjologicznym, wiąże się ze zmianą liczby synchronicznie działających komórek. Wzór (Equation 42) sugeruje, że potencjał od źródeł odległych zanika z odległością jak 1/R[math]^2[/math]. Warto zauważyć, że dla warstw dipolowych bardzo dużych rozmiarów, zanik ten może być jeszcze wolniejszy. Np. dla nieskończonej warstwy dipolowej potencjał nad (lub pod warstwą) dipolową jest stały i nie zmienia się z odległością. Oznacza to, że dla małych odległości od warstwy, w porównaniu z jej rozmiarami, zanik potencjału będzie niewielki, a im większa warstwa tym zanik potencjału wolniejszy. W przypadku dużych warstw dipolowych zanik potencjału na czaszce względem potencjału na korze jest nieznaczny. Eksperymentalnie obserwowany stosunek potencjału na korze do potencjału na czaszce jest, w większości spontanicznych zapisów EEG, pomiędzy 2 i 5 (Cooper et al., 1965). Po uwzględnieniu niejednorodności takich jak czaszka, płyn mózgowo-rdzeniowy i powietrzne nad głową, oznacza to, że korowe źródła muszą tworzyć warstwy dipolowe o rozmiarach znacznie większych niż odległość pomiędzy czaszką a korą. Mają więc one rozmiary rzędu paru cm[math]^2[/math].
Podsumowanie
Potencjały w ośrodku jednorodnym pochodzące od źródeł i zlewów prądowych zostały otrzymane na podstawie ogólnego równania (Equation 30). Fizjologiczne źródła prądowe, są generowane w błonach komórkowych w wyniku transmisji synaptycznej lub generacji potencjału czynnościowego. Różne konfiguracje źródeł i zlewów mogą generować potencjały o bardzo różnych własnościach przestrzennych. Zanik potencjału wraz z odległością od źródeł-zlewów może być bardzo słaby (tzw. pola dalekie lub długozasięgowe), jak w przypadku warstwy dipolowej. Zanik ten może też być silny np. w przypadku koncentrycznie ustawionych neuronów, tak jak w przypadku kwadrupola (tzw. pola bliskie lub krótkozasięgowe). Znajomość potencjałów generowanych w wyidealizowanym, nieskończonym, jednorodnym ośrodku dostarcza przydatnych oszacowań na temat różnych fizjologicznych procesów np. generacji potencjałów czaszkowych EEG. Na koniec należy zauważyć, że wszystkie wyprowadzone tutaj wzory dotyczyły potencjału w pewnym punkcie. W rzeczywistości, mierzone potencjały są potencjałami uśrednionymi po całej objętości elektrody. Potencjał mierzony przez sferyczną elektrodę [math]\Phi_E[/math] o promieniu R jest związany z teoretycznym potencjałem punktowym [math]\Phi[/math] poprzez całkę objętościową:
Ze względu na skomplikowaną anatomię kory, zachowanie potencjału [math]\Phi_E[/math] wewnątrz mózgu (zapisy śródmózgowe) będzie bardzo silnie zależało od parametru skali R. W przeciwieństwie do tego, potencjały czaszkowe są już silnie uśrednione przestrzennie w wyniku przejścia przez płyn mózgowo-rdzeniowy, czaszkę i skórę. Powoduje to, że rozmiar elektrody nie ma prawie wpływu na zapis czynności EEG.
Literatura
Bok S.T., Histonomy of the Cerebral Cortex, Elsevier, New York, 1959.
Cooper R., Winter A.L., Crow H.J., Walter W.G. Comparison of subcortical, cortical and scalp activity using chronically indwelling electrodes in man. Electroencephalogr Clin Neurophysiol. 18:217-228, 1965.
Elul R. The genesis of the EEG. Int Rev Neurobiol 15: 227-272, 1972.
Jewett D.L. Volume-conducted potentials in response to auditory stimuli as detected by averaging in the cat. Electroencephalogr. Clin. Neurophysiol. 28(6):609-618, 1970.
Nunez P.L Electric Fields of the Brain. The Neurophysics of EEG. Oxford University Press, New York, NY, 1981 (First edition).
Nunez P.L. Neocortical Dynamics and Human EEG Rhythms. Oxford University Press, New York, 1995.
Scholl D.A. The organization of the Cerebral Cortex, Methuen, London, 1956.