FizykaII NI/Ćwiczenia I
Zadanie 1
Podaj infinitezymalny element przesunięcia w płaskim układzie kartezjańskim oraz układzie biegunowym. Oblicz masę okręgu o promieniu [math]R[/math], który wykonano z nieskończenie cienkiego drutu. Rozkład masy przypadającej na jednostkę długości okręgu opisuje wzór: [math]\lambda (\Phi) =\lambda_0 \Phi[/math], gdzie [math]\lambda[/math] — gęstość liniowa masy, [math]\Phi[/math] — kąt liczony od osi poziomej układu kartezjańskiego.
Zadanie 2
Podaj infinitezymalny element powierzchni w płaskim układzie kartezjańskim, układzie biegunowym, trójwymiarowym układzie kartezjańskim, układzie cylindrycznym oraz układzie sferycznym. Oblicz masę nieskończenie cienkiego krążka o promieniu R. Rozkład masy przypadającej na jednostkę powierzchni krążka opisuje wzór σ(r)=σ0r, gdzie σ — gęstość powierzchniowa masy, r — odległość od środka krążka.
Zadanie 3
Oblicz gradient następującego pola skalarnego: [math]\Phi_{x,y,z}=x^2+y^2+z^2[/math]
Zadanie 4
Wysokość pewnego wzgórza (patrz rysunek poniżej) wyraża się następującym wzorem:[math]h(x,y)=10(2xy-3x^2-4y^2-18x+28y+12)[/math]
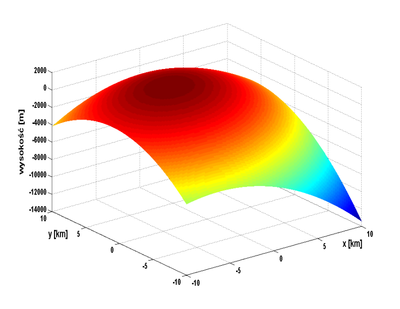 Oblicz:
Oblicz:
- Gdzie znajduje się szczyt wzniesienia?
- Jaka jest wysokość szczytu?
- Jaka jest szybkość zmian wysokości wzniesienia (wyrażona w metrach na kilometr) w punkcie o współrzędnych [math]x = 1 km[/math], [math]y = 1km[/math]. W którym kierunku, liczonym od tego punktu, wysokość rośnie najszybciej?
Zadanie 5
Oblicz dywergencję następujących pól wektorowych:
- [math] A_{x, y, z}=(x^2,y,2z)[/math]
- [math]A_{x, y, z}=(\sin(x),\sin(z),\sin(y)) [/math]
Zadanie 6
Oblicz rotację pola wektorowego o postaci: [math]A=\left[ x, 2z+y^2, y^2z-x^2\right][/math].
Zadanie 7
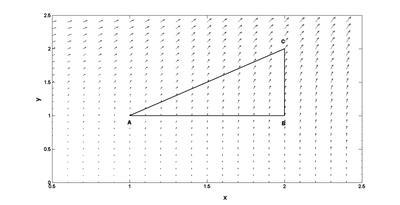
Oblicz całkę krzywoliniową pola wektorowego [math]A=y^2\hat{e}_x+(2xy+1)\hat{e}_y[/math] wzdłuż krzywych biegnących od punktu [math]a=(1,1)[/math], do punktu [math]b=(1,2)[/math]; od punktu [math]b=(1,2)[/math], do punktu [math]c=(2,2)[/math] i od punktu [math]c[/math] do punktu [math]a[/math] (krzywa [math]y = x[/math], patrz rysunek poniżej).