FizykaII NI/Ćwiczenia XII
Zadanie 1
Kondensator o pojemności [math]C=\unit{1}{\mu F}[/math], w którym początkowo zmagazynowano energię [math]\unit{0,5}{J}[/math], rozładowuje się przez opornik o oporze [math]\unit{1}{M\Omega}[/math].
- Ile wynosi początkowy ładunek na kondensatorze?
- Ile wynosi natężenie prądu płynącego przez opornik, gdy zaczyna się rozładowanie?
- Oblicz różnicę potencjałów UC na kondensatorze i UR na oporniku, w zależności od czasu.
- Wyznacz szybkość wytwarzania energii termicznej, w zależności od czasu.
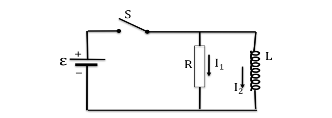
Zadanie 2
W obwodzie przedstawionym na rysunku klucz [math]S[/math] został zamknięty w chwili [math]t=0[/math]. Od tego czasu źródło prądu stałego utrzymuje stałe natężenie prądu [math]I[/math] przepływającego przez zamknięty klucz.
- Wyprowadź natężenie prądu w cewce jako funkcję czasu.
- Wykaż, że w chwili [math]t = \frac{L}{R}\ln 2[/math] natężenie prądu w oporniku jest równe natężeniu prądu w cewce.
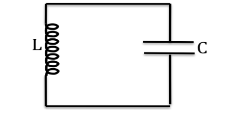
Zadanie 3
W obwodzie drgającym LC, składającym się z kondensatora o pojemności [math]\unit{1}{nF}[/math] i cewki o indukcyjności [math]\unit{3}{mH}[/math] maksymalne napięcie na okładkach kondensatora wynosi [math]\unit{3}{V}[/math].
- Ile wynosi maksymalny ładunek na okładkach kondensatora?
- Ile wynosi maksymalne natężenie prądu w obwodzie?
- Ile wynosi maksymalna energia, zmagazynowana w polu magnetycznym cewki?
- Naszkicuj zmiany w czasie obydwu energii, [math]E_E[/math] i [math]E_B[/math].
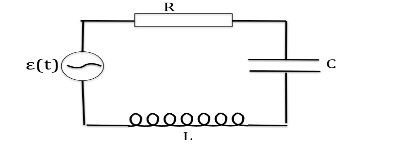
Zadanie 4
Do połączonych szeregowo oporu [math]R[/math], indukcyjności [math]L[/math] oraz pojemności [math]C[/math] przyłożone jest napięcie sinusoidalnie zmienne [math]\epsilon(t )[/math] o częstości [math]\omega[/math]. Podaj impedancję obwodu, jej moduł i przesunięcie fazowe.