FizykaII OO/Dyfrakcja światła
Pokazy
- Dyfrakcja światła laserowego na szczelinie.
- Dyfrakcja światła laserowego na otworze i włosie.
- Interferencyjno dyfrakcyjny obraz światła dyfrakcyjnego przechodzącego przez dwie szczeliny.
Dyfrakcja na pojedynczej szczelinie o szerokości [math]d[/math]
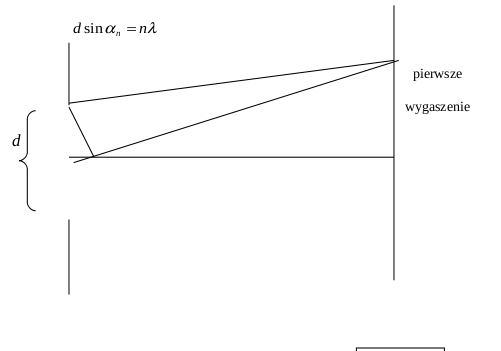
Zakładamy, że przez szczelinę przechodzi światło monochromatyczne o długości fali [math]\lambda[/math]. Dzielimy obszar szczeliny na pary źródeł odległe od siebie o d/2. Posługując się zasadą Huygensa, która mówi o tym, że każdy punkt do którego dotrze zaburzenie falowe staje się źródłem nowej fali kulistej przeprowadzamy rozumowanie dla jednej pary źródeł. Światło dociera do ekranu i pojawiają się na nim wzmocnienia i wygaszenia. Dokładnie naprzeciw środka szczeliny pojawi się prążek jasny, ponieważ od każdej pary źródeł docierają fale zgodne w fazie, bo różnica dróg optycznych pomiędzy nimi jest równa zeru. Pierwsze minimum na ekranie będzie w miejscu, gdzie od pary źródeł oddalonych o d/2 dotrą fale o przeciwnej fazie. Różnica dróg optycznych jest równa
[math] \frac{d}{2}\sin\alpha = \frac{\lambda}{2}[/math]
gdzie [math]\alpha[/math] jest kątem pod którym widać pierwsze minimum.
Dla kolejnych minimów mamy warunek:
[math]\frac{d}{2}\sin\alpha_n = n\frac{\lambda}{2}[/math],
czyli
[math]d \sin\alpha_n = n\lambda[/math]
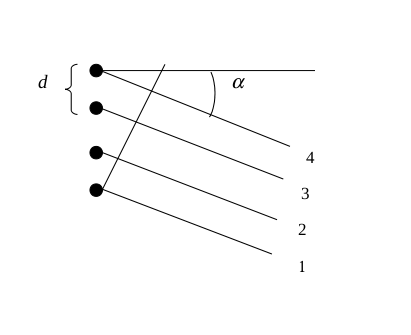
Dyfrakcja światła monochromatycznego wychodzącego z 4 punktowych źródeł odległych o d od siebie
Szukamy obrazu interferencyjnego, który powstaje z nałożenia się 4 fal kulistych znajdujących się w dużej odległości od źródeł. Źródła są punktowe odległe od siebie o d.
Obraz powstaje na odległym ekranie.
[math]r_2=r_1+d\sin\alpha[/math]
[math]r_3=r_1+2d\sin\alpha[/math]
[math]r_4=r_1+3d\sin\alpha[/math]
[math]r_i[/math] — odległość źródeł od ekranu
Cztery funkcje falowe mają postać:
[math]U_1=\frac{A}{r_1}\cos(kr_1-\omega t)[/math]
[math]U_2=\frac{A}{r_2}\cos(kr_1+kd\sin\alpha-\omega t)[/math]
[math]U_3=\frac{A}{r_3}\cos(kr_1+2kd\sin\alpha-\omega t)[/math]
[math]U_4=\frac{A}{r_4}\cos(kr_1+3kd\sin\alpha-\omega t)[/math]
[math]A(r) =\frac{A}{r_{sr}}[/math] — uśrednienie amplitudy
[math]U_1+U_4=2\frac{A}{r_{sr}}\cos(kr_1+\frac{3}{2}kd\sin\alpha-\omega t)\cos\left[ -\frac{3}{2}d\sin\alpha\right][/math]
[math]U_2+U_3=2\frac{A}{r_{sr}}\cos(kr_1+\frac{3}{2}kd\sin\alpha-\omega t)\cos\left[ -\frac{1}{2}d\sin\alpha\right][/math]
[math]\cos\left[ -\frac{3}{2}d\sin\alpha\right]+\cos\left[ -\frac{1}{2}d\sin\alpha\right]=2\cos(d\sin\alpha)\cos\frac{d\sin\alpha}{2}[/math]
[math] U_1+U_2+U_3+U_4 = \frac{A}{r_{sr}}\cos(kr_1+\frac{3}{2}kd\sin\alpha -\omega t)\frac{\sin(2kd\sin\alpha)}{\sin\frac{kd\sin\alpha}{2}}[/math]
Uogólnienie dla N szczelin, czyli dla siatki dyfrakcyjnej:
[math]\sum_{i=1}^N U_i = \frac{A}{r_{sr}}\cos\left( kr_1+k\frac{N-1}{2}d\sin\alpha-\omega t\right)\frac{\sin\frac{Nkd\sin\alpha}{2}}{\sin\frac{kd\sin\alpha}{2}}[/math]
[math]A_{TOTAL} = frac{A}{r_{sr}}\frac{\sin\frac{Nkd\sin\alpha}{2}}{\sin\frac{kd\sin\alpha}{2}}[/math] — amplituda fali będącej wynikiem interferencji.
Dyskusja wzoru dla N szczelin
Warunki na wzmocnienia i wygaszenia. Główne wzmocnienie pojawia się, gdy sinus w mianowniku dąży do zera.
[math] \frac{kd\sin\alpha}{2}=\pi n[/math]
[math] k = \frac{2\pi}{\lambda}[/math]
[math] d\sin\alpha = n\lambda[/math]
Warunek dla maksimów bocznych — licznik znika, a mianownik dąży do zera.
[math]\frac{Nkd\sin\alpha}{2}=M\pi[/math]
[math]kd\sin\alpha = \frac{2M\pi}{N}[/math]
[math]d\sin\alpha = \frac{M\lambda}{N}[/math]
W siatkach dyfrakcyjnych interesują nas maksyma główne nie boczne, ale należy zdawać sobie sprawę, że wynik jaki obserwujemy jest obrazem dyfrakcyjno-interferencyjnym.