FizykaII OO/Interferencja światła
Pokazy
- filtry interferencyjne,
- doświadczenie Younga,
- interferencja na cienkich warstwach.
Filtr interferencyjny
Filtr interferencyjny składa się z trzech warstw: dwóch zewnętrznych przepuszczających światło i cienkiej warstwy środkowej o grubości równej połowie długości fali, która odbija wszystkie długości fali z wyjątkiem jednej.
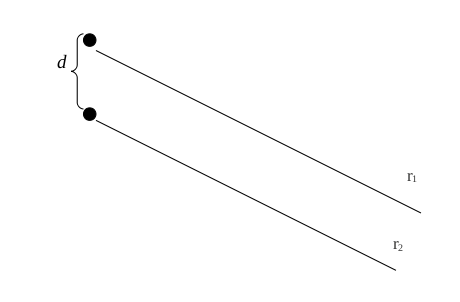
Interferencja światła monochromatycznego z dwóch źródeł
[math]U_1(r,t)=A(r_1)\cos(kr_1-\omega t)[/math]
[math]U_2(r,t)=A(r_2)\cos(kr_2-\omega t)[/math]
[math] U = U_1(r,t)+U_2(r,t)=A(r_1)\cos(kr_1-\omega t)+A(r_2)\cos(kr_2-\omega t)=[/math]
[math]2A_{sr}\cos\frac{kr_1-\omega t+kr_2-\omega t}{2}\cos\frac{kr_1-\omega t-kr_2+\omega t}{2} =2A_{sr}\cos\left[\frac{k}{2}(r_1-r_2)-\omega t\right]\cos\ \frac{k}{2}(r_1-r_2)[/math]
Obraz zależy od odległości [math]r_1[/math] i [math]r_2[/math].
Warunki na ekstremum
Wartość amplitudy jest maksymalna, gdy
[math]\cos\ \frac{k}{2}(r_1-r_2)=\pm 1[/math]
[math]k\frac{r_1-r_2}{2}=n\pi[/math]
[math]r_1-r_2=n\lambda[/math]
To jest warunek na maksimum interferencyjne
[math]\cos\frac{k}{2}(r_1-r_2) =0[/math]
[math]\frac{k}{2}(r_1-r_2) = \left(n+\nicefrac{1}{2}\right)\pi[/math]
[math]r_1-r_2=\left(n+\nicefrac{1}{2}\right)\lambda[/math]
Powyższe równanie przedstawia warunek na minimum interferencyjne.
[math]r_1-r_2 = r_{sr} +\frac{d}{2}\sin\alpha -r_{sr}+\frac{d}{2}\sin\alpha = d\sin\alpha[/math]
Jeśli źródła są odległe o d i obserwujemy obraz pod kątem to warunki przyjmują prostszą postać.
[math]d\sin\alpha = n\lambda[/math]
[math]d\sin\alpha = \left(n+\nicefrac{1}{2}\right)\lambda[/math]
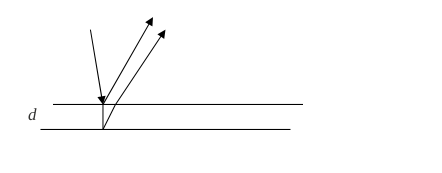
Interferencja na cienkich warstwach
Gdy światło pada na cienką warstwę, to następuje interferencja promienia odbitego od powierzchni i promienia, który wszedł do warstwy i odbił się od drugiej powierzchni granicznej.
Różnica dróg optycznych jest w przybliżeniu równa 2d, a warunek na wzmocnienie interferencyjne ma postać:
[math]2d\sin\alpha = \left(n+\nicefrac{1}{2}\right)\lambda[/math]
a na wygaszenie:
[math]2d=n\lambda[/math]
Warunki dlatego mają taką postać, że jeden promień odbija się od ośrodka o większej gęstości, a drugi od ośrodka o mniejszej gęstości. W tym pierwszym wypadku następuje zmiana fazy o .