FizykaII OO/Obrazy w soczewkach

Zjawisko załamania światła w szkle jest wykorzystane w soczewkach.

Soczewki mogą być: skupiające i rozpraszające światło. Szklana soczewka dwuwypukła lub płasko-wypukła umieszczona w powietrzu ma właściwości skupiające. Szklana soczewka dwuwklęsła lub płasko-wklęsła umieszczona w powietrzu ma właściwości rozpraszające. Soczewki są elementami układów przetwarzających światło. Wytwarzają — podobnie jak zwierciadła — obrazy powiększone lub zmniejszone, rzeczywiste lub pozorne. Przez soczewki światło przechodzi i załamuje się w nich.

Soczewka jest bryłą symetryczną i można wyróżnić prostą określającą tę symetrię. Prosta prostopadła do soczewki poprowadzona tak, że soczewkę można wokół niej obrócić o dowolny kąt i nie zmieni to właściwości soczewki, nazywa się osią optyczną. Jeśli mówimy o wiązce równoległej, to mamy na myśli wiązkę równoległą do osi optycznej. Po przejściu przez soczewkę skupiającą wiązka promieni równoległych leżących blisko osi przechodzi przez punkt zwanym ogniskiem. Soczewki, podobnie jak zwierciadła, wykazują aberrację sferyczną.

Równoległa wiązka światła — po przejściu przez soczewkę rozpraszającą — staje się rozbieżna, a więc promienie nie przecinają się. Soczewka ta ma ognisko pozorne, które jest punktem przecięcia się przedłużeń promieni załamanych w soczewce.

Odwrotność ogniskowej nazywa się zdolnością zbierającą soczewki [math]Z=\frac{1}{Z}[/math]. Jednostką tej wielkości jest dioptria (D) [math]\unit{1}{D}=\unit{1}{m^{-1}}[/math].

Jeśli złożymy ze sobą kilka soczewek, to zdolność zbierająca takiego układu [math]Z_u[/math] jest równa sumie zdolności zbierających poszczególnych soczewek:

[math]Z_u=Z_1+Z_2+\ldots+Z_n[/math]

Powiększenie

to stosunek wysokości obrazu H do wysokości przedmiotu h.

[math] p=\frac{H}{h}[/math]

Jest to wielkość, której używa się przy konstrukcji obrazów zarówno w soczewkach jak i zwierciadłach. [math]p\lt 1[/math] oznacza obraz zmniejszony, [math]p\gt 1[/math] — obraz powiększony, [math]p=1[/math] — obraz tej samej wielkości. Z analizy konstrukcji obrazów w zwierciadłach i soczewkach wynika, że [math]\frac{H}{h}=|\frac{x}{y}|[/math], by określić powiększenie, wystarczy porównać odległości obrazu i przedmiotu od soczewki (lub zwierciadła).

Konstrukcja obrazu rzeczywistego w soczewce skupiającej.

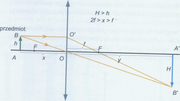
Rysunek pokazuje konstrukcję obrazu powiększonego, rzeczywistego i odwróconego w soczewce. Posłuży on nam również do wyprowadzenia równania soczewki. Na rysunku dają się zauważyć dwie pary trójkątów podobnych: Trójkąty ABO i A’B’O oraz OO’F i A’B’F. Z podobieństwa pierwszej pary trójkątów wynika proporcja: [math]\frac{x}{y}=\frac{AB}{A'B'}[/math], a z drugiej [math]\frac{OO'}{A'B'} = \frac{f}{y-f}[/math]. Poniaważ [math]OO'=AB[/math] na mocy konstrukcji, więc otrzymujemy równanie

[math]\frac{x}{y} =\frac{f}{y-f}[/math]

Stąd [math]xy-xf=yf[/math]. Po podzieleniu obu stron ostatniego równania przez iloczyn [math]xyf[/math], otrzymujemy:

[math]\frac 1 f = \frac 1 x +\frac 1 y[/math]

Równanie soczewki jest identyczne jak równanie zwierciadła.

• [math]f\gt 0[/math] — soczewka skupiająca,
• [math]f\lt 0[/math] — soczewka rozpraszająca.

Konwencja znaków x i y jest taka sama jak dla zwierciadeł.

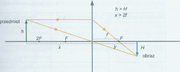
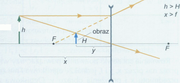
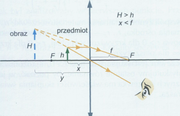
Rysunki poniżej przedstawiają konstrukcję obrazów w soczewkach skupiających i rozpraszających, a tabela zawiera podsumowanie informacji o obrazach.

Ustawienie przedmiotu	Ustawienie obrazu	Cechy obrazu
[math]x\lt f[/math]	Obraz po tej samej stronie co przedmiot [math]|y|\gt x[/math]	Pozorny, prosty, powiększony
[math]2f\gt x\gt f[/math]	[math]y\gt 2f[/math]	Rzeczywisty, powiększony, odwrócony
[math]x=2f[/math]	[math]y=2f[/math]	Rzeczywisty, odwrócony, o wielkości równej wielkości przedmiotu
[math]x\gt 2f[/math]	[math]f\lt y\lt 2f[/math]	Rzeczywisty, odwrócony, zmniejszony
wiązka promieni przyosiowych	promienie załamane w soczewce przechodzą przez ognisko [math]y=f[/math]	Brak obrazu
[math]x=f[/math]	Promienie załamane w soczewce tworzą wiązkę równoległą do osi

Figure 2: Cechy obrazów uzyskiwanych w soczewkach skupiających.

Konstrukcja obrazu rzeczywistego zmniejszonego w soczewce skupiającej.

Konstrukcja obrazu pozornego w soczewce rozpraszającej.

Konstrukcja obrazu pozornego w soczewce skupiającej.

Równanie soczewki pozwoliło powiązać trzy wielkości oznaczane przez nas przez x, y i f, jednakże ogniskowa f nie zależy od położenia przedmiotu x i położenia obrazu y. Ogniskowa zależy od kształtu soczewki i od współczynnika załamania materiału, z jakiego jest wykonana oraz współczynnika załamania ośrodka, w jakim ją umieszczono.

[math]\frac 1 f = \left(\frac{n_0}n-1\right)\left(\frac 1{r_1}+\frac 1 {r_2}\right)[/math]

n — współczynnik załamania materiału soczewki, [math]n_0[/math] — współczynnik załamania ośrodka, [math]r_1[/math], [math]r_2[/math] — promienie krzywizny soczewki, zgodnie z umową:

• [math]r\gt 0[/math] dla krzywizny wypukłej,
• [math]r\lt 0[/math] dla krzywizny wklęsłej,
• [math]r\rightarrow 0[/math] dla płaszczyzny.

Soczewka jest rozpraszająca, jeśli [math]f\gt 0[/math], a skupiająca, gdy [math]f\lt 0[/math]. Przedyskutujmy ostatnie równanie, by poznać w jakich warunkach fizycznych soczewka ma właściwości skupiania światła, a kiedy je rozprasza.

Soczewka skupiająca, [math]f\gt 0[/math]

Wzór Equation 1 jest dodatni w dwu przypadkach:

• oba wyrażenia są dodatnie:
  • [math]\frac{n_0}n-1\gt 0[/math], [math]n\gt n_0[/math]
  • [math]\frac 1{r_1}+\frac 1 {r_2}\gt 0[/math], wyrażenie to jest większe od zera w trzech wypadkach:
    • [math]r_1\gt 0[/math], [math]r_2\gt 0[/math] — soczewka dwuwypukła,
    • [math]r_1\gt 0[/math], [math]r_2\rightarrow\infty[/math] — soczewka płasko-wypukła

  Przykładem może być szklana soczewka dwuwypukła umieszczona w powietrzu lub w wodzie.

• oba wyrażenia są ujemne:
  • [math]\frac{n_0}n-1\lt 0[/math], [math]n\lt n_0[/math]
  • [math]\frac 1{r_1}+\frac 1 {r_2}\gt 0[/math], wyrażenie to jest ujemne w trzech przypadkach:
    • [math]r_1\lt 0[/math], [math]r_2\lt 0[/math] — soczewka dwuwklęsła,
    • [math]r_1\lt 0[/math], [math]r_2\rightarrow\infty[/math] — soczewka płasko-wklęsła,
    • [math] r_1\lt 0[/math], [math]r_2\gt 0[/math], [math]|r_1|\lt |r_2|[/math] — soczewka wklęsło-wypukła.

  Przykładem takiej soczewki skupiającej jest pęcherz powietrza w szkle o kształcie soczewki dwuwklęsłej.

Soczewka rozpraszająca, [math]f\lt 0[/math]

Wzór Equation 1 jest ujemny, gdy jeden człon jest ujemny, a drugi dodatni:

• [math]\frac{n_0}n-1\lt 0[/math], tzn. [math]n\lt n_0[/math], oraz [math]\frac 1{r_1}+\frac 1 {r_2}\gt 0[/math]. Ten warunek określający kształty soczewek był przeanalizowany w pierwszym punkcie poprzedniego rozdziału. Przykładem takiej soczewki rozpraszającej jest pęcherz powietrza w szkle, o kształcie soczewki dwuwypukłej.
• [math]\frac{n_0}n-1\gt 0[/math], tzn. [math]n\gt n_0[/math], oraz [math]\frac 1{r_1}+\frac 1 {r_2}\lt 0[/math]. Kształty soczewek zostały omówione w punkcie drugim poprzedniego rozdziału. Przykładem może być soczewka dwuwklęsła szklana w powietrzu.