FizykaI FMiN/Bryła sztywna 1
Bryła sztywna
Bryła sztywna
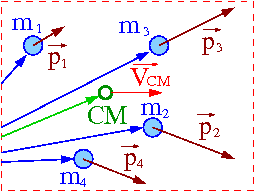
Układ wielu ciał
Rozważaliśmy już poprzenio zagadnienie ruchu układu wielu ciał (w inercjalnym układzie odniesienia).
Zdefiniowaliśmy
- masę układu
- [math] M \; = \; \sum_i m_i [/math]
- położenie środka masy:
- [math] \vec{R} \; = \; \frac{1}{M}\sum_i m_i \;\vec{r}_i [/math]
Do opisu ruchu układu jako całości możemy wprowadzić
- pęd układu
- [math] \vec{P} \; = \; M\; \vec{V}_{CM} [/math]
- energię kinetyczną układu jako całości
- [math]E_k \; = \; \frac{M \; {V}_{CM}^2}{2} \; + \; E_k^\star [/math]
gdzie [math]E_k^\star[/math] oznacza energię "wewnętrzna" (energię kinetyczną związaną z ruchem elementów układu względem siebie)
- moment pędu układu
- [math]\vec{L} \; = \; M \vec{R}_{CM} \times \vec{V}_{CM} \; + \; \vec{L}_{CM}^\star [/math]
gdzie [math]\vec{L}_{CM}^\star[/math] oznacza "wewnętrzny" moment pędu
W oparciu o te pojęcia możemy opisać ruch układu jako całości stosując równania ruchu punktu materialnego:
- [math]\frac{d \vec{P}}{dt} \; = \; \vec{F}^{zw} [/math]
- [math]\frac{d \vec{L}}{dt} \; = \; \vec{M}^{zw} [/math]
Natomiast ruch względny ciał układu może być (w ogólnym przypadku) bardzo skomplikowany...
Definicja
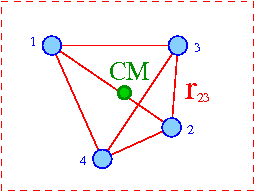
Szczególnym przypadkiem układu wielu ciał jest układ, w którym względne odległości między poszczególnymi elementami układu są stałe:
- [math] r_{ij} \; = \; \left| \vec{r}_i - \vec{r}_j \right| \; = \; const [/math]
Układ taki możemy nazywać bryłą sztywną.
Na ogół ciałem sztywnym nazywamy ciało makroskopowe, które nie podlega deformacjom (lub występujące deformacje są pomijalnie małe). Zakładamy, że wszystkie punkty mają względem siebie stałe odległości.
Położenie
Aby jednoznacznie określić położenie bryły sztywnej w przestrzeni nie wystarczy (w ogólnym przypadku) podać wektor położenia jej środka masy.
Spróbujmy określić ile parametrów potrzebnych jest do opisania jej położenia. Aby "unieruchomić" bryłę sztywną musimy podać:
- położenie wybranego punktu tego ciała np. środka masy
- opisują je 3 parametry (stopnie swobody), np. współrzędne x,y,z
- położenie drugiego wybranego punktu tego ciała
- ponieważ odległość między dwoma punktami jest ustalona wystarczą do tego 2 parametry (położenie na sferze)
- położenie trzeciego punktu, niewspółliniowego z poprzednimi
- przy ustalonej pozycji pierwszych dwóch punktów bryła może jedynie obracać się wokół przechodzącej przez nie osi - położenie określa 1 parametr (położenie na okręgu)
Po ustaleniu położenia trzech niewspółliniowych punktów bryły wszystkie kolejne będą już miały ustaloną pozycję (zadaną przez wzajemne odległości).
Położenie bryły sztywnej opisuje wiec 6 parametrów (mamy 6 stopni swobody): 3 współrzędne i 3 kąty.
Opis ruchu
Złóżenie ruchów
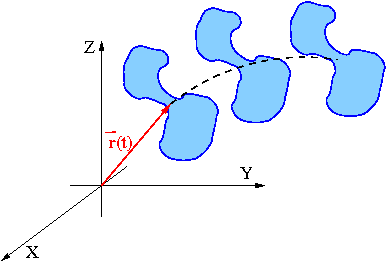
Ogólny ruch (zmianę położenia) można przedstawić jako złożenie ruchu postępowego oraz ruchu obrotowego.
W ruchu postępowym wektory prędkości są takie same dla wszystkich punktów ciała.
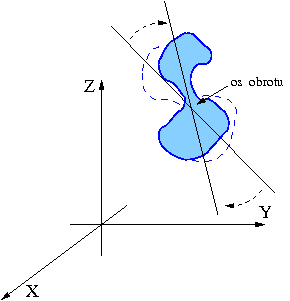
W ruchu obrotowym wszystkie punkty poruszają się po okręgach wokół wybranej osi obrotu (najczęściej jest nią środek masy ciała).
Prędkość każdego punktu bryły można zapisać w postaci
- [math] \vec{v}_i \; = \; \vec{V}_{CM} \; + \; \vec{\omega} \times \left( \vec{r}_i - \vec{R} \right) [/math]
- gdzie [math]\vec{V}_{CM}[/math] jest prędkością środka masy, a
[math]\vec{\omega}[/math] prędkościa kątową w ruchu obrotowym wokół środka masy.
Chwilowa oś obrotu
Czasami złożenie ruchu postepowego i obrotowego można przedstawić jako ruch obrotowy względem chwilowej osi obrotu.
Jeśli [math]\vec{V}_{CM} \perp \vec{\omega}[/math] wtedy możemy zapisać:
- [math] \vec{v}_i \; = \; \vec{\omega} \times \left( \vec{r}_i - \vec{R}' \right) [/math]
- gdzie [math]\vec{R}'[/math] określa położenie chwilowej osi obrotu (zmienne w czasie!)
Więzy
Ruch bryły sztywnej w ogólnycm przypadku także opisuje 6 parametrów (np. prędkość środka masy i prędkość kątowa w układzie środka masy)
W wielu zagadnieniach ruch bryły sztywnej jest jednak ogranicznony
przez więzy, które redukują liczbę
stopni swobody.
Przykładowo:
- koło obracające się na nieruchomej osi ⇒ jeden stopień swobody (kąt obrotu)
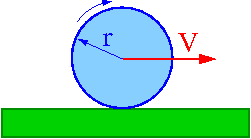
- walec toczący się bez poślizgu ⇒ jeden st. swobody (kąt obrotu lub przesunięcie)
- walec toczący się z poślizgiem ⇒ dwa stopnie swobody (kąt obrotu i przesunięcie)
- kulka toczące się bez poślizgu ⇒ trzy stopnie swobody (trzy składowe [math]\vec{\omega}[/math])
W rozwiązywaniu zagadnień kluczowe jest zrozumienie jakie są stopnie swobody Obecność więzów oznacza też obecność sił reakcji więzów...
Statyka
Warunek równowagi
Bryła sztywna pozostaje nieruchoma, wtedy i tylko wtedy, gdy działające na nią siły i momenty sił równoważą się:
- [math]\vec{F}^{zw} \; = \; \sum_i \vec{F}^{zw}_i \; = \; 0 \;\;\; \Longleftrightarrow \;\;\; \frac{d \vec{P}}{dt} \; = \; 0 [/math]
- [math] \vec{M}^{zw} \; = \; \sum_i \vec{M}^{zw}_i \; = \; 0 \;\;\; \Longleftrightarrow \;\;\; \frac{d \vec{L}}{dt} \; = \; 0 [/math]
Przy czym jeśli wypadkowa sił zewnętrznych znika,
[math]\vec{F}^{zw} = 0[/math],
to wypadkowy moment sił
względem każdej osi jest taki sam:
- [math] \vec{r}'_i \; = \; \vec{r}_i \; + \; \vec{R} [/math]
- [math] \vec{M}' \; = \; \sum_i \vec{r}'_i \times \vec{F}_i \; = \; \sum_i \vec{r}_i \times \vec{F}_i + \vec{R} \times \sum_i \vec{F}_i \; = \; \vec{M} [/math]
Wystarczy sprawdzić warunek równowagi względem jednej osi
Siłami z którymi naogół bedziemy mieli do czynienia w zagadnieniach równowagi bryły sztywnej są siła ciężkości i siły reakcji więzów.
Rodzaje równowagi
Nawet jeśli warunek [math]\vec{F}^{zw} = \vec{M}^{zw} = 0[/math] jest spełniony, równowaga może być:
Nieznaczne (infintezymalne) wychylenie bryły z położenia równowagi powoduje
w przypadku równowagi
- trwałej
- pojawienie się siły wypadkowej (momentu siły) przywracającej równowagę
- obojętnej
- zmianę położenia równowagi
- chwiejnej
- pojawienie się siły wypadkowej zwiększającej wychylenie
Przykład I
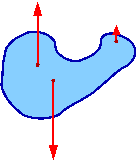
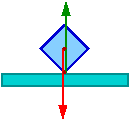
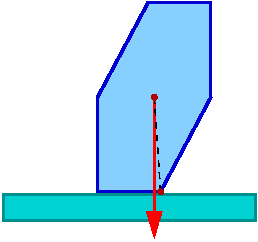
Warunkiem równowagi trwałej dla wielościanu (ustawionego na poziomej powierzchni, pod działaniem siły ciężkości) jest aby pion wypuszczony ze środka ciężkości przechodził przez podstawę.
Gdy pion przechodzi przez podstawę mamy równowagę trwałą
Moment siły ciężkości "dociska" bryłę do powierzchni.
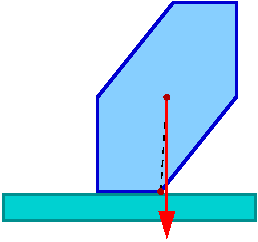
Gdy pion wychodzi poza obrys podstawy mamy do czynienia z brakiem równowagi
Moment siły ciężkości wywraca bryłę
Przykład II
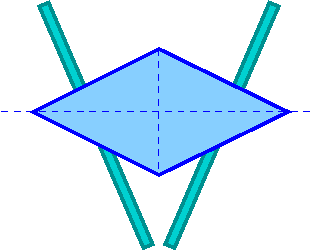
Dwu-stożek położony na nierównoległych szynach:
Gdy szyny są poziome, stożek będzie się poruszał w kierunku szerszego końca.
Szyny stykają się ze stożkiem wzdłuż łuku elipsy z osią stożka (środkiem masy) w jednym z ognisk. Siła ciężkości i reakcji szyn się równoważą, ale wypadkowy moment sił nie będzie zerowy.
Równowagę obojętną osiągniemy gdy szyny będą pochylone pod odpowiednim
kątem (szerszy koniec wyżej)
Oś stożka pozostaje cały czas na tej samej wysokości ([math]E_p = const[/math])
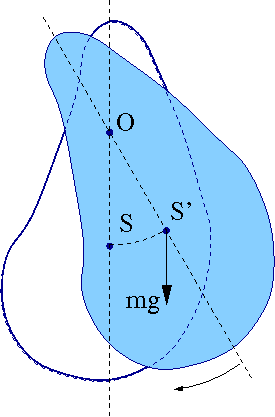
Rodzaje równowagi a energia
Równowagę bryły na którą działa siła ciężkości i siły reakcji można sklasyfikować obserwując położenie środka masy (czyli zmiany energi potencjalnej).
Nieznaczne (infintezymalne) wychylenie bryły z położenia równowagi powoduje:
- równowaga trwała
- podniesienie środka masy i wzrost energii potencjalnej
- równowaga obojętna
- brak zmian położenia środka masy
- równowaga chwiejna
- obniżenie środka masy i zmniejszenie energii potencjalnej
Zmiana położenia środka masy,
przy wychyleniu z położenia równowagi,
zależy od kształtu bryły,
ale także od charakteru więzów.
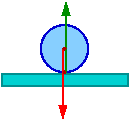
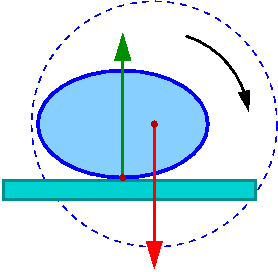
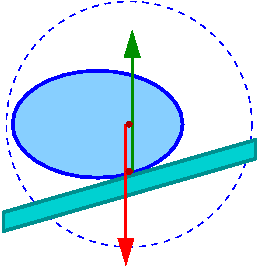
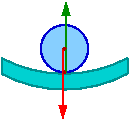
Np: równowaga kuli zależy od kształtu powierzchni na której leży
Typ równowagi zależy od zmiany położenia środka masy ([math]\vec{F} = -grad E_p[/math])
Kryterium zmiany położenia środka masy (zmiany energii potencjalnej) ma zastosowanie także w bardziej ogólnych przypadkach.
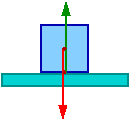
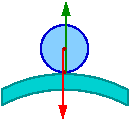
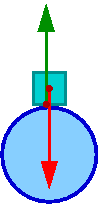
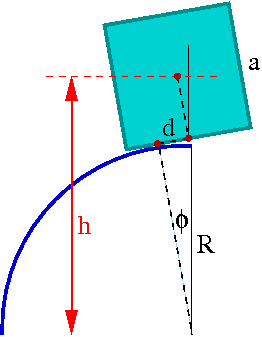
Przykład: sześcian ustawiony na kuli
Położenie środka masy sześcianu (nad środkiem kuli) wyraża się zależnością
- [math] h \; = \; R\; \cos \phi \; + \; d\; \sin \phi \; + \; \frac{1}{2} a \; \cos\phi [/math]
Przy wychyleniu punkt podparcia sześcianu przesunie się o
- [math] d \; = \; R \; \phi [/math]
Uzyskujemy więc
- [math] h \; = \; \left( R + \frac{a}{2} \right) \; \cos \phi \; + \; R \; \phi \; \sin \phi [/math]
W przybliżeniu małych kątów ([math]\sin\phi \approx \phi[/math], [math]\cos\phi \approx 1 - \frac{1}{2}\phi^2[/math])
- [math] h \; = \; \left( R + \frac{a}{2} \right) \; + \; \frac{1}{2} \left( R - \frac{a}{2} \right) \cdot \phi^2 [/math]
Równowaga będzie trwała jeśli człon kwadratowy w kącie wychylenia będzie dodatni (wzrost energii), czyli dla
- [math]R \gt \frac{a}{2}[/math]
Prawa ruchu
Obrót wokół ustalonej osi
Dla bryły sztywnej obracającej się wokół ustalonej osi mement pędu (skalarnie):
- [math] L \; = \; \omega \sum_i m_i \; r_{\perp \;i}^2 \; = \; \omega \; I[/math]
gdzie [math]\omega = \frac{d\phi}{dt} [/math] jest prędkością kątową, a [math] r_{\perp\;i}[/math] opisuje odległość masy [math]i[/math] od osi obrotu,
[math]I[/math] jest momentem bezwładności względem wybranej osi.
Ruch jednostajnie przyspieszony
Pod wpływem stałego momentu siły [math]M[/math]:
- [math] M \; = \; \frac{dL}{dt} \; = \; \frac{d\omega}{dt} \sum_i m_i \; r_{\perp \;i}^2 = \varepsilon \; I [/math]
Bryła obraca się ze stałym przyspieszeniem kątowym ([math]\varepsilon = \frac{d\omega}{dt} [/math])
- [math] \varepsilon \; = \; \frac{M}{I} = const [/math]
Przyjmując, że moment bezwładności jest stały ([math]I[/math]=const) bryła będzie się obracać ruchem jednostajnie przyspieszonym.
Podobnie jak w przypadku ruchu postępowego
- przyspieszenie kątowe jest proporcjonalne do przyłożonego momentu siły
- zwiększenie siły lub zwiększenie jej ramienia powoduje wzrost przyspieszenia
- przyspieszenie kątowe jest odwrotnie proporcjonalne do momentu bezwładności
- zwiekszenie masy lub zwiększenie jej odległości od osi obrotu powoduje zmniejszenie przyspieszenia
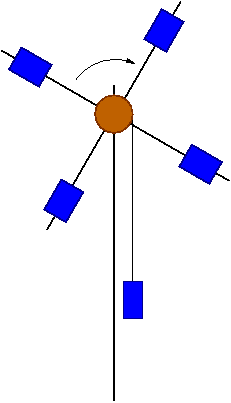
Ruch harmoniczny
Pokaz
Moment siły zależy od kąta skręcenia pręta [math]\phi[/math]:
- [math] M \; = \; - \xi \; \phi [/math]
gdzie [math]\xi[/math] - współczynnik "sprężystości"; moment siły ma znak przeciwny do skręcenia.
Moment siły możemy też wyrazić poprzez przyspieszenie kątowe:
- [math] M \; = \; \frac{dL}{dt} \; = \; \frac{d\omega}{dt} \; I = \frac{d^2\phi}{dt^2} \; I [/math]
Przyrównując otrzymujemy równanie oscylatora harmonicznego:
- [math] \frac{d^2\phi}{dt^2} \; = \; - \; \frac{\xi}{I} \; \phi [/math]
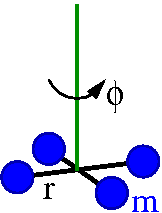
Częstość drgań:
- [math] \nu \; = \; \sqrt{\frac{\xi}{I}} \; = \; \frac{\sqrt{\xi}}{\sqrt{ \sum_i m_i \; r_{\perp \;i}^2}} \; \approx \; \frac{\sqrt{\xi}}{2 r \sqrt{ m} } [/math]
W ramach pokazu pokazano, że częstość maleje (okres rośnie) przy wzroście masy lub wzroście odległości od osi obrotu.
Moment bezwładności
Przyspieszenie kątowe w ruchu bryły sztywnej zależy nie tylko od masy całkowitej, ale także od jej rozłożenia względem osi obrotu.
Rozkład masy względem wybranej osi obrotu (najczęściej przechodzącej przez środek masy, ale nie koniecznie) opisuje moment bezwładności
- [math] I \; = \; \sum_i m_i \; r_{\perp \;i}^2 [/math]
W przypadku ciągłego rozkładu masy sumę zastępujemy całką po objętości:
- [math] I \; = \; \int dV \; \rho \; r_{\perp }^2 [/math]
Dla ciała jednorodnego ([math]\rho[/math] = const = [math]\frac{M}{V}[/math]) można to również zapisać w postaci:
- [math] I \; = \; \frac{M}{V} \int dV \; \; r_{\perp }^2 \; = \; M \; \frac{\int dV \; r_{\perp }^2 }{\int dV } \; = \; M \langle r_{\perp }^2 \rangle [/math]
gdzie [math]\langle r_{\perp }^2 \rangle[/math] jest średnim kwadratem odległości od osi obrotu.
Tymsamym stosunek momentu bezwładności do masy zależy tylko od kształtu i rozmiarów ciała:
- [math] \frac{I}{M} = \langle r_{\perp }^2 \rangle [/math]
Dla wielu brył stosunek ten możemy wyznaczyć z prostych rozważań geometryczntych.
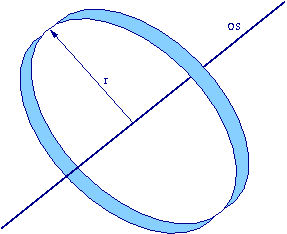
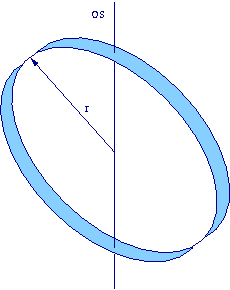
Obręcz (pusta w środku)
- obrót wokół osi symetrii
- Wszystkie punkty równoodległe od osi:
- [math] \langle r_{\perp }^2 \rangle \; = \; r^2 \; \Rightarrow \; I_\perp \; = \; M \; r^2 [/math]
- obrót wokół średnicy
Oznaczmy oś obrotu jako oś X, a średnicę prostopadłą do osi obrotu jako oś Y
Z definicji obręczy i symetrii mamy:
- [math] x^2 + y^2 \; = \; r^2[/math] i
- [math]\langle x^2\rangle \; = \; \langle y^2 \rangle [/math]
Możemy zatem wyznaczyć średni kwadrat odległości od osi
- [math] \langle r_{\perp }^2 \rangle \; = \; \langle y^2 \rangle \; = \; \frac{1}{2} \; r^2 \qquad \Rightarrow \qquad I_\parallel \; = \; \frac{1}{2} \;M \; r^2 [/math]
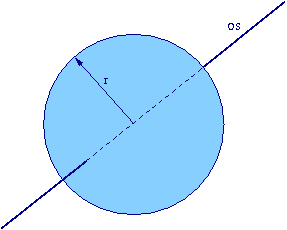
Sfera (powierzchnia kuli)
obrót wokół osi symetrii
- [math] x^2 + y^2 + z^2 \; = \; r^2[/math] i
- [math] \langle x^2\rangle \; = \; \langle y^2 \rangle \; = \; \langle z^2 \rangle [/math]
Uzyskujemy:
- [math] \langle r_{\perp }^2 \rangle \; = \; \langle x^2 + y^2 \rangle \; = \; \frac{2}{3} \; r^2 \qquad \Rightarrow \qquad I \; = \; \frac{2}{3} \;M \; r^2 [/math]
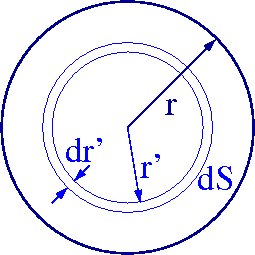
Koło (krążek)
obrót wokół osi symetrii
Koło można traktować jako sumę wielu obręczy ⇒ musimy wyznaczyć śrenią po powierzchni koła z [math]r^2[/math]:
- [math] \langle r_{\perp }^2 \rangle \; = \; \frac{\int r'^2 \cdot dS}{S} \; = \; \frac{1}{\pi r^2} \int r'^2 \cdot 2 \pi r' dr' \; = \; \frac{2 \pi}{\pi r^2} \; \frac{1}{4}r^4 \; = \; \frac{1}{2} \; r^2 [/math]
Ostatecznie uzyskujemy
- [math] I_\perp \; = \; \frac{1}{2} \;M \; r^2 [/math]
Podobnie można wyznaczyć [math]I[/math] dla innych brył:
Prostokąt
Obrót wokół osi prostopadłej, przechodzącej przez środek
- [math] I_\perp = \frac{1}{12} \;M \; (a^2 + b^2) [/math]
Pręt
Obrót wokół osi prostopadłej, przechodzącej przez środek
- [math]I = \frac{1}{12} \;M \; l^2[/math]
Kula (jednorodna)
- [math]I = \frac{2}{5} \;M \; r^2[/math]
Twierdzenie o osiach równoległych
Zazwyczaj liczymy moment bezwładności względem osi przechodzącej przez środek ciężkości S (wszystkie podane dotychczas przykłady)
Bryła może jednak wirować wokół dowolnej osi...
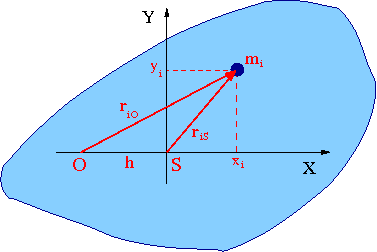
Niech układ wspórzędnych XY będzie układem środka masy.
Moment bezwładności względem osi równoległej 0,
odległej o [math]h[/math] od osi
S można wyznaczyć rozpisując odległości
elementów masy od osi O
- [math] r_{i O}^2 = (x_i+h)^2 + y_i^2 \; = \; h^2 + 2hx_i + r_{iS}^2 [/math]
Moment bezwładności wyraża się przez sumę:
- [math] I_O = \sum_i m_i r_{i O}^2 = h^2 \sum_i m_i \; + \; 2h \sum_i m_i x_i + \sum_i m_i r_{iS}^2 [/math]
Z definicji środka masy drugi człon znika
- [math]\sum_i m_i x_i =0[/math]
Otrzymujemy wzór nazywany twierdzeniem o osiach równoległych lub Twierdzeniem Steinera
- [math] I_O \; = \; I_S \; + \; M \; h^2 [/math]
Prawa ruchu
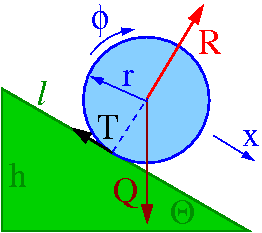
Równia pochyła
W przypadku staczania po równi pochyłej bez poślizgu symetrycznej bryły (obręczy, waleca, kuli...) mamy jeden stopień swobody. Przsunięcie związane jest z kątem obrotu:
- [math] x = r \; \phi [/math]
i podobna zależność wiąże przyspieszenie liniowe i kątowe
- [math] a = r \; \varepsilon [/math]
Wzdłuż równi działa siła tarcia i równoległa składowa siły ciężkości.
Równanie dla ruchu postępowego możemy zapisać w postaci
- [math] m a \; = \; Q \; \sin \theta \; - \; T [/math]
Natomiast dla ruchu obrotowego (jedynie siła tarcia daje moment siły względem środka masy):
- [math] I\; \varepsilon \; = \; T \;r [/math]
Eliminując siłę tarcia z pierwszego równania:
- [math] m a \; + \; \frac{I \varepsilon}{r} \; = \; m g \; \sin \theta [/math]
Z czego możemy wyznaczyć przyspieszenie liniowe: [math] a \; = \; \frac{ g \; \sin \theta }{1 + \frac{I}{m r^2} } [/math]
Im większy moment bezwładności, tym wolniej stacza się ciało...
Dla przykładu: pełny walec ([math] I = \frac{1}{2} M r^2[/math]) stacza się szybciej niż rura ([math] I = M r^2[/math]), a wolniej niż kula ([math] I = \frac{2}{5} M r^2[/math]).
Zagadnienie staczania ciała po równi można rozwiązać w równoważny sposób
korzystając z chwilowej osi obrotu i twierdzenia Steinera.
Względem chwilowej osi obrotu
(linia styku bryły z równią)
jedynie siła ciężkości daje niezerowy moment siły.
Zapiszmy równanie ruchu obrotowego względem tej osi:
- [math] I_o\; \varepsilon \; = \; Q \; \sin \theta \cdot r [/math]
Z twierdzenia Steinera:
- [math] I_o \; = \; I \; + \; m \; r^2 [/math]
Otrzymujemy:
- [math] a \; = \; r \; \varepsilon \; = \; \frac{m g \; \sin \theta\; r^2}{ I_o } [/math]
- [math] \; = \; \frac{ m r^2 \; g \; \sin \theta }{mr^2 + I} [/math]
Wahadło fizyczne
Równanie małych drgań bryły sztywnej,
wokół osi obrotu O
przechodzącej w odległości [math]l[/math]
od środka ciężkości S:
- [math] I_o \; \varepsilon \; = \; - m g \sin \phi \cdot l [/math]
- [math] \left( I + ml^2 \right) \; \frac{d^2 \phi}{dt^2} \; \approx \; - m g l \; \phi [/math]
gdzie skorzystalimy z przybliżenia małych drgań ([math]\sin \phi \approx \phi [/math])
Częstość drgań (z równania oscylatora harmonicznego) wynosi:
- [math] \nu \; = \; \sqrt{\frac{mgl}{I+ ml^2}} \; = \; \sqrt{\frac{g}{l (1 + \frac{I}{ml^2})}} [/math]
Częstość ta odpowiada częstości drgań wahadła matematycznego o długości:
- [math]l_z = l (1 + \frac{I}{ml^2})[/math]
gdzie [math]l_z[/math] nazywamy długością zredukowaną wahadła
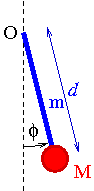
Rozważmy wahadło w postaci pręta o masie m i długości d, na którego końcu zamocowano punktową masę M.
Równanie małych drgańwokół osi obrotu O:
- [math] I_o \; \varepsilon \; = \; - M d g \sin \phi - m \frac{d}{2} g \sin \phi [/math]
W przybliżeniu małych drgań:
- [math] \left( M d^2 + \frac{1}{3}md^2 \right) \; \frac{d^2 \phi}{dt^2} \; \approx \; - (M + \frac{m}{2}) d g \; \phi [/math]
Częstość drgań wyraża się więc wzorem:
- [math] \nu \; = \; \sqrt{\frac{g}{l}} \cdot \sqrt{\frac{M+\frac{1}{2}m}{M+\frac{1}{3}m}} \;\; \approx \; \sqrt{\frac{g}{l}} \cdot \left(1 + \frac{1}{12} \cdot \frac{m}{M}\right)[/math]
gdzie przybliżenie jest słuszne w granicy [math]m \ll M[/math].
Długość zredukowana wahadła
- [math]l_z = d \; \frac{M+\frac{1}{3}m}{M+\frac{1}{2}m} \approx d \cdot \left(1 - \frac{1}{6} \cdot \frac{m}{M}\right)[/math]
Energia ruchu obrotowego
Energia kinetyczna układu ciał:
- [math]E_k \; = \; E_k^\star \; + \; \frac{M \; {V}_{CM}^2}{2} [/math]
Dla bryły sztywnej energia "wewnętrzna" jest energią kinetyczną ruchu obrotowego względem środka masy:
- [math] E_k^\star \; = \; \frac{1}{2}\; \sum_i m_i v_i^2 \; = \; \frac{1}{2}\; \sum_i m_i ( r_i \;\omega )^2 \; = \; \frac{1}{2}\; \omega^2 \; I \; = \; \frac{1}{2}\; \omega \; L [/math]
W przypadku ciała toczącego się bez poślizgu ([math]v = \omega \; r[/math]) otrzymujemy
- [math]E_k \; = \; \frac{m v^2}{2} \; + \; \frac{I \omega^2}{2} \; = \; \frac{m v^2}{2} \left(1 + \frac{I}{mr^2}\right) [/math]
Ruch (np. staczanie z równi pochyłej) odbywa się tak, jak dla punktu materialnego o efejtywnej masie bezwładnej
- [math]m \; \left(1 + \frac{I}{mr^2}\right)[/math]
i niezmienionej masie grawitacyjnej
Dla przykładu: prędkość jaką uzyska ciało staczające się bez poślizgu z równi o wysokości [math]h[/math] można wyznaczyć z zasady zachowania energii:
- [math] m g h \; = \; \frac{1}{2} m v^2 \left(1 + \frac{I}{mr^2}\right)[/math]
Otrzymujemy
- [math]v \; = \; \sqrt{\frac{2gh}{1 + \frac{I}{mr^2} }} [/math]
Przyspieszenie możemy wyznaczyć zauważając (ruch jednostajnie przyspieszony), że prędkość średnia jest równa połowie prędkości końcowej:
- [math] a = \frac{v}{t} = \frac{v^2}{2l} \; = \; \frac{2gh}{2l\left(1 + \frac{I}{mr^2}\right) } \; = \; \frac{g \; \sin \theta }{1 + \frac{I}{mr^2}} [/math]
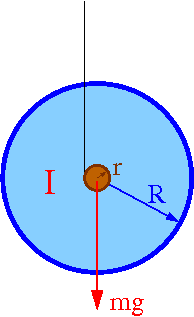
Koło Maxwella
Koło o promieniu R "toczy się" po osi o promieniu r.
Jak w przypadku równi pochyłej (tylko kładąc [math]\theta = \frac{\pi}{2}[/math])
- [math] a \; = \; \frac{g}{1 + \frac{I}{mr^2}} [/math]
Zakładając, że masa skupiona jest praktycznie w całości na obręczy
- [math] I \; = \; m R^2 [/math]
otrzymujemy wyrażenie na przyspieszenie liniowe
- [math] a \; = \; g \; \frac{r^2}{R^2 + r^2} \ll g [/math]
Przyspieszenie liniowe wielokrotnie mniejsze od przyspieszenia w spadku swobodnym...
Energia potencjalna zamienia się głównie na energię ruchu obrotowego.
Porównanie
Ruch postępowy punktu materialnego i ruch obrotowy bryły sztywnej (względem ustalonej osi, pokrywającej się z osią symetrii) opisane są bardzo podobnymi zależnościami. Poniższa tabela powinna pomóc w zrozumieniu tych analogii
| ruch postępowy | ruch obrotowy | ||
|---|---|---|---|
| wielkość | wyrażenie | wielkość | wyrażenie |
| przesunięcie | [math]\vec{x} [/math] | kąt obrotu | [math]\vec{\phi} [/math] |
| prędkość | [math]\displaystyle \vec{v} = \frac{d\vec{x}}{dt}[/math] | prędkość kątowa | [math]\displaystyle \vec{\omega} = \frac{d\vec{\phi}}{dt}[/math] |
| przyspieszenie | [math]\displaystyle \vec{a} = \frac{d\vec{v}}{dt}[/math] | przyspieszenie kątowe | [math]\displaystyle \vec{\varepsilon} = \frac{d\vec{\omega}}{dt}[/math] |
| masa | [math]m[/math] | moment bezwładności | [math]I[/math] |
| pęd | [math]\vec{p} = m \vec{v}[/math] | moment pędu | [math]\vec{L} = I \vec{\omega}[/math] |
| układ izolowany | [math] \vec{p} = const[/math] | układ izolowany | [math] \vec{L} = const[/math] |
| siła | [math]\vec{F}[/math] | moment siły | [math]\vec{M}[/math] |
| równania ruchu | [math]\displaystyle \vec{F} = m\vec{a}[/math] | równania ruchu | [math]\displaystyle \vec{M} = I \vec{\varepsilon}[/math] |
| [math]\displaystyle \frac{d\vec{p}}{dt} = \vec{F}[/math] | [math]\displaystyle \frac{d\vec{L}}{dt} = \vec{M}[/math] | ||
| praca | [math]\displaystyle W = \int \vec{F} \cdot d\vec{x} [/math] | praca | [math]\displaystyle W = \int \ \vec{M} \cdot d\vec{\phi} [/math] |
| energia kinetyczna | [math] E_k = \frac{1}{2} m v^2 [/math] | energia kinetyczna | [math] E_k = \frac{1}{2} I \omega^2 [/math] |