FizykaI FMiN/Dynamika laws
Prawa ruchu: dynamika
Spis treści
Bezwładność
- Bezwładność (inercja)
- właściwość układu fizycznego (ciała) charakteryzująca jego podatność na zmiany stanu (ruchu)
- (Encyklopedia PWN 1998)
Bezwładność przejawia się na dwa sposoby:
- dążenie układu do zachowania stanu, w którym się znajduje
- dążenie ciał do pozostawania w spoczynku lub w ruchu
- "opór" stawiany przez układ, gdy próbujemy zmienić jego stan
- np. gdy próbujemy wprawić w ruch lub zatrzymać ciało
I zasada dynamiki
Zasada bezwładności
I zasada dynamiki, inaczej zwana Zasadą bezwładności
została sformułowana przez Isaaca Newtona
w dziele: "Zasady matematyczne filozofii
naturalnej" (1687)
( Philosophiae Naturalis Principia Mathematica)
"Każde ciało trwa w swym stanie spoczynku lub ruchu prostoliniowego i jednostajnego, jeśli siły przyłożone nie zmuszają ciała do zmiany tego stanu."
Zasada bezwładności w ujęciu Newtona ma dwie "wady":
- przyjmuje, że można zdefiniować bezwzględny spoczynek i ruch
- zakłada, że na ciało mogą nie działać żadne siły
Układ odniesienia
Newton zakładał istnienie "przestrzeń absolutna", która "pozostaje zawsza taka sama i nieruchoma"
- [math]\Rightarrow[/math] "absolutnego" układu odniesienia
Dziś wiemy, że taki układ nie istnieje. Powstaje więc pytanie: względem jakiego układu spełniona jest I zasada dynamiki ?
Jeśli dwa układy poruszają się względem siebie z przyspieszeniem, I zasada dynamiki nie może być spełniona w obu z nich...
Ciało izolowane
Aby na ciało nie działały żadne siły musi być całkowicie odizolowane od wpływu innych ciał. Ale w realnym świecie bardzo trudno o taką "doskonałą" izolację.
Wszystkie znane nam siły makroskopowe maleją z odległością
- [math]\Rightarrow[/math] ciało uznamy za izolowane jeśli będzie dostatecznie daleko od innych ciał.
Jednak aby zweryfikować zasadę bezwładności musimy mieć dwa ciała izolowane:
- ciało obserwowane i
- układ odniesienia (obserwatora).
Z jednej strony ciała te muszą być od siebie dostatecznie daleko, żeby wyeliminować wszelki wpływ, a z drugiej strony dostatecznie blisko, żeby możliwa była obserwacja.
Zauważmy też, że każda obserwacja jest związana z jakimś oddziaływaniem!
W rzeczywistym doświadczeniu nigdy nie spełnimy idealnych warunków izolacji ciała.
Ale możemy stworzyć warunki, w których oczekiwane odstępstwa będą bardzo bardzo małe...
Układ inercjalny
Układ w którym obowiązuje I zasada dynamiki nazywamy układem inercjalnym.
Jeśli istnieje jeden układ inercjalny to istnieje nieskończenie wiele układów inercjalnych!
Inercjalny będzie także każdy inny układ poruszający się względem niego z prędkością [math]\vec{V} = const[/math]
Zasada bezwładności jest równoważna z postulatem:
| Istnieje układ inercjalny |
Jaki układ możemy uznać za inercjalny ?
Wszystko zależy od rozważanego zagadnienia i dokładności pomiaru.
Na ogół wystarcza układ laboratoryjny, czyli układ zwiazany z Ziemią.
Niemniej, w przypadku precyzyjnych pomiarów możemy zaobserwować efekty związane z ruchem obrotowym Ziemi. Powodują one, że układ związany z powierzchnią Ziemi nie jest ściśle inercjalny.
W takiej sytuacji, a także w przypadku rozpatrywania ruch Księżyca lub satelitów Ziemi, lepszym wyborem jest układ odniesienia związany ze środkiem Ziemi. Ale i on nie jest ściśle inercjalny, bo Ziemia porusza się z przyspieszeniem dookoła Słońca. Także układ związany ze Słońcem nie jest ściśle inercjalny na skutek rotacji Galaktyki...
| Układ odniesienia | Inercjalność ograniczona przez | Przyspieszenie |
|---|---|---|
| Powierzchnia Ziemi | Rotację Ziemi | [math]a_Z \approx 0.03 \; \frac{m}{s^2}[/math] |
| Środek Ziemi | Obieg wokół Słońca | [math]a_S \approx 0.006 \; \frac{m}{s^2}[/math] |
| Słońce | Rotację Galaktyki | [math]a_G \approx 0.000\; 000\; 000\; 3 \; \frac{m}{s^2}[/math] |
II zasada dynamiki
II prawo Newtona
"Zmiana ruchu jest proporcjonalna do przyłożonej siły poruszającej i odbywa się w kierunku prostej, wzdłuż której siła jest przyłożona"
Zmiana ruchu ciała (w układzie inercjalnym)
jest zawsze wynikiem oddziaływania otoczenia (innych ciał)!
Oddziaływanie to opisujemy ilościowo wprowadzając pojęcie siły
Siła jest wielkością wektorową (istotna jest nie tylko wartość, ale i kierunek zmiany ruchu).
Siły możemy porównywać ilościowo bez konieczności wprawiania ciał w ruch.
Naogół wykorzystujemy przy tym I zasadę dynamiki (równowaga sił).
Przykładem jest porównywanie ciężaru poprzez ważenie ciał,
pomiar siły dynamometrem...
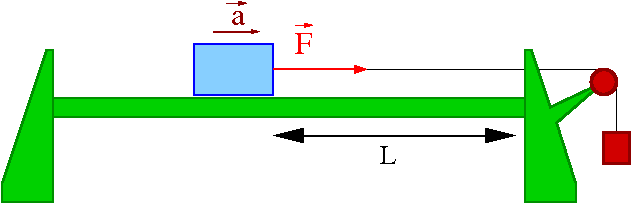
Ruch pod wpływem stałej siły
Rozważmy ciało P, na które działają kolejno różne siły [math]\vec{F}[/math] nadając mu różne przyspieszenia [math]\vec{a}[/math]
Dla uproszczenia wybierzmy układ odniesienia tak, że [math]\vec{r}(0) = \vec{v}(0) = 0[/math]. W takiej sytuacji ciało będzie się poruszać ruchem prostoliniowym, jednostajnie przyspieszonym
Zgodnie z II zasadą Newtona przyspieszenie jest proporcjonalne do działającej siły
- [math] a \; = \; \frac{d^2 x }{d t^2} \; \sim \; F [/math]
Czas na pokonanie zadanej odległości L:
- [math]L = \frac{a}{2} \; t_1^2 \; \Rightarrow \; t_1^2 = \frac{2L}{a} [/math]
Prędkość uzyskana przez ciało na końcu odcinka L:
- [math] v_1 = \frac{2L}{t_1} \; \Rightarrow \; a = \frac{v_1^2}{2L} [/math]
Porównując uzyskane przez ciało prędkości możemy porównywać przyspieszenia, a stąd wnioskować o wartości siły.
Możemy wybrać jakąś siłę, jako jednostkową i w ten sposób ilościowo określić wartości pozostałych sił.
Doświadczenie potwierdza (pokaz na wykładzie), że prędkość uzyskiwana przez ciało rośnie jak pierwiastek przyłożonej siły (cztery razy większa siła nadaje dwa razy większą prędkość).
Masa bezwładna
Rozważmy sytuację, w której ustalona siła [math]\vec{F}[/math] diałając na różne ciała P nadaje im różne przyspieszenia [math]\vec{a}[/math].
Możemy wprowadzić współczynniki m, które określają stosunki przyspieszeń różnych ciał
- [math] a_1 : a_2 : a_3 : \ldots \; = \; \frac{1}{m_1} : \frac{1}{m_2} : \frac{1}{m_3} : \ldots [/math]
Lub też:
- [math] m_1 \; a_1 \; = \; m_2 \; a_2 \; = \; m_3 \; a_3 \; = \; \ldots [/math]
Doświadczenie potwierdza (pokaz na wykładzie), że stosunki przyspieszeń
zależą od badanych ciał ale nie zależą
od przyłożonej siły.
Możemy wybrać jakieś ciało i uznać je za "jednostkowe". Tak wybrane współczynkiki nazywamy masą bezwładną ciała.
| m - masa bezwładna |
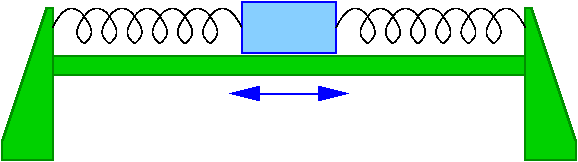
Ruch harmoniczny
Pokaz
Wózek na torze powietrznym przyczepiony do sprężyny
Siła z jaką działa sprężyna zależy wyłącznie od położenia wózka
| [math]F_x \; = \; - k \cdot x[/math] |
Przyjmijmy, że położeniem równowagi jest
[math]x=0[/math]
Jeśli w chwili początkowej ciało znajduje się w położeniu [math]x(0) = R [/math] i [math]v_x(0)=0[/math], wtedy jego ruch (run harmoniczny) opisany jest zależnością:
- [math] x(t) \; = \; R \cdot \cos (\omega t) [/math]
- [math] a(t) \; = \; - \omega^2 \cdot x(t) \qquad \omega = \frac{2 \pi}{T} [/math]
Mierząc okres drgań możemy więc wnioskować o przyspieszeniu ciała:
- [math] a \; \sim \; T^{-2} [/math]
Zgodnie z drugą zasada dynamiki oczekujemy, że:
- [math] a \; \sim \; \frac{1}{m} \; \Rightarrow \; T^2 \sim m[/math]
Wyniki pomiarów (pokaz na wykładzie; masa wózka zwiększana poprzez doczepianie odważników) potwierdzają, że kwadrat okresu drgań rośnie liniowo z masą.
Siła
Jednostką masy bezwładnej jest kilogram, 1 kg
Druga zasada dynamiki Newtona definiuje pojęcie siły
(klasyczna definicja siły):
| [math]\vec{F} \; = \; m \; \vec{a}[/math] |
Jednostka siły: 1 niuton
- [math]1 \; N\; = \; 1 \; kg \cdot 1 \; \frac{m}{s^2}[/math]
Druga zasada dynamiki jest:
- wnioskiem z doświadczeń
- definicją nowych wielkości: masy i siły
Zasada niezależności działania sił
Jeśli na ciało o masie [math]m[/math] działają dwie niezależne siły [math]F_1[/math] i [math]F_2[/math]:
- [math] \left.\begin{array}{l} \vec{F}_1 = m \vec{a}_1 \\[5mm] \vec{F}_2 = m \vec{a}_2 \end{array}\right\} \; \Rightarrow \; \vec{F}_1 + \vec{F}_2 = m ( \vec{a}_1 + \vec{a}_2 ) [/math]
- ⇒ przyspieszenie wywołane przez siłę wypadkową jest równe sumie przyspieszeń
Zasada addytywności masy
Jeśli dwie siły działając na dwie masy wywołują równe przyspieszenie:
- [math]\left. \begin{array}{l} \vec{F}_1 = m_1 \vec{a} \\[5mm] \vec{F}_2 = m_2 \vec{a} \end{array} \!\! \right\} \; \Rightarrow \; \vec{F}_1 + \vec{F}_2 = (m_1 + m_2) \vec{a} [/math]
- ⇒ siła wypadkowa w działani na całkowitą masę daje takie samo przyspieszenie
Masa jest wielkością addytywną: wypadkowa masa układu ciał równa jest sumie mas.
Uogólnienie
Druga zasada dynamiki Newtona w postaci "klasycznej"
| [math]\vec{F} \; = \; m \; \vec{a}[/math] |
ważna jest tylko dla ciał których masa jest stała [math]m \; = \; const[/math]
Możemy jednak uogólnić:
- [math] \vec{F} \; = \; m \; \frac{d\vec{v}}{dt} \; \begin{array}{c} _{m=const} \\ = \\ ~ \end{array} \; \frac{d(m \vec{v})}{dt} \; = \; \frac{d\vec{p}}{dt} [/math]
gdzie [math]\vec{p} = m \vec{v}[/math] - pęd cząstki
Uogólniona zasada dynamiki:
| [math]\vec{F} \; = \frac{d\vec{p}}{dt}[/math] |
jest słuszna także dla ciał o zmieniającej się masie (np. rakieta) oraz w przypadku relatywistycznym (choć zmieni się definicja pędu ciała!).
Z powyższej zależności wynika, że zmiana pędu ciała pod wpływem działającej siły równa jest tzw. popędowi siły:
- [math] \Delta \vec{p} \; = \; \int\limits_{\Delta t} \vec{F} \; dt [/math]
III zasada dynamiki
Zasada akcji i reakcji
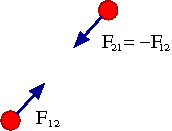
"Każdemu działaniu towarzyszy równe i przeciwnie skierowane przeciwdziałanie.
Wzajemne oddziaływania dwóch ciał są zawsze równe sobie i skierowane przeciwnie."
| [math] \vec{F}_{12} \; = \; - \vec{F}_{21} [/math] |
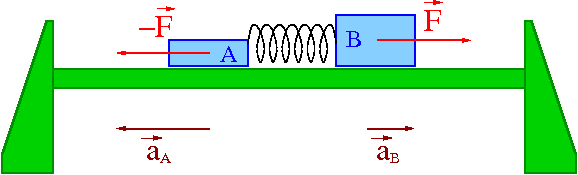
Pokaz
Dwa wózki na torze połączone sprężyną
Siły akcji i reakcji są równe co do wartości.
Przyspieszenia są odwrotnie proporcjonalne do mas:
- [math] \vec{F}_A \; = \; -\vec{F}_B [/math]
- [math] m_A \; \vec{a}_A \; = \; - m_B \; \vec{a}_B [/math]
- [math] a_A : a_B \; = \; \frac{1}{m_A} : \frac{1}{m_B} [/math]
Siły akcji i reakcji są przejawem oddziaływanie między dwoma ciałami
⇒ pary sił działające na różne ciała (!).
Przykład
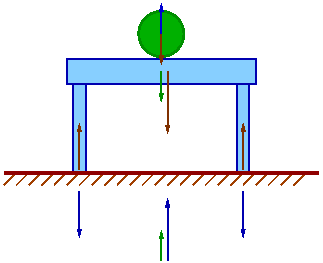
Kula leżąca na stole stojącym na ziemi
Pary sił akcji-reakcji:
- nacisk kuli na stół - siła reakcji stołu
- nacisk stołu na podłogę - siła reakcji podłogi
ale także
- ciężar kuli - siła przyciągania Ziemi przez kulę
- ciężar stołu - siła przyciągania Ziemi przez stół
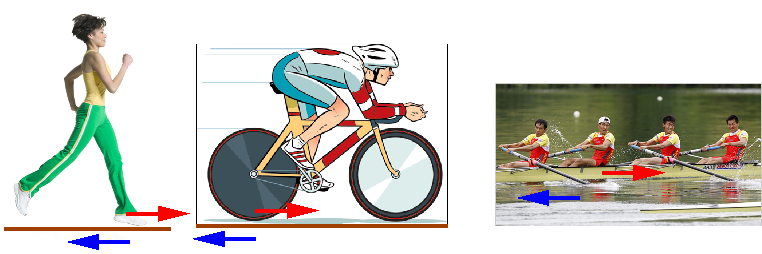
Poruszamy się także dzięki siłom reakcji...
Idąc, jadąc na rowerze czy wiosłując działamy siłą na ziemię (wodę) starając się ją odepchnąć. To siła reakcji powoduje nasz ruch!
Siła wyporu
Pokaz
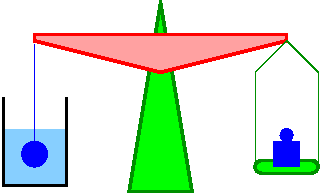
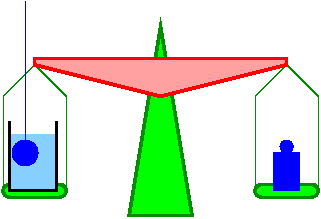
Ciało zanurzone w cieczy traci na wadze...
- [math]\Rightarrow[/math] Ciecz działa na ciało siłą wyporu
Ale ciecz w której ciało zanurzamy "przybiera" na wadze...
- [math]\Rightarrow[/math] ciało działa na ciecz...
III zasada dynamiki mówi nam, że łączny ciężar cieczy i ciała musi pozostać niezmieniony...
Statyka
Ciało spoczywa, jeśli działające na niego siły równoważą się (I zasada dynamiki).
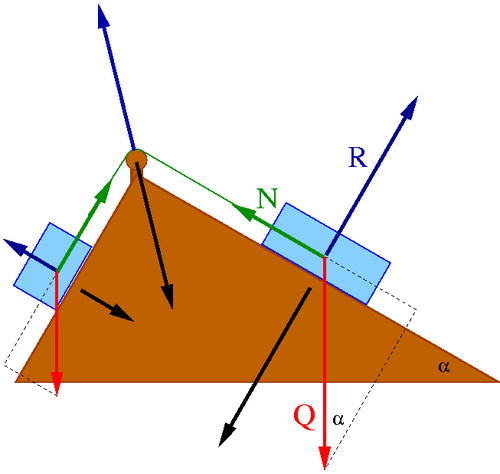
W przypadku ciała na równi, siła ciężkości równoważona jest przez siłę reakcji równi i napięcie sznurka:
- [math] R \; = \; Q \cdot \cos \alpha [/math]
- [math] N \; = \; Q \cdot \sin \alpha [/math]
Pomijamy tu siły tarcia, zakładamy też, że sznurek jest równoległy do równi.
Ciało spoczywa, jeśli działające na niego siły równoważą się.
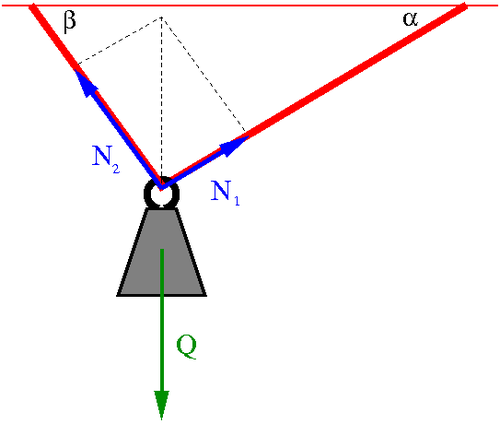
Równowaga w pionie:
- [math] Q \; = \; N_1 \sin \alpha \; + \; N_2 \sin \beta [/math]
Równowaga w poziomie:
- [math] N_1 \cos \alpha \; = \; N_2 \cos \beta [/math]
Otrzymujemy:
- [math] N_1 \; = \; \frac{Q \cos \beta }{\sin (\alpha + \beta)} [/math]
Dla [math]\beta = \alpha [/math]:
- [math] N_1 \; = N_2 \; = \; \frac{Q }{2 \sin (\alpha)} [/math]
Nie jest możliwe naciągnięcie liny tak, by była dokładnie poziomo
[math]\beta = \alpha = 0[/math]
Ruch
Jeśli ciało porusza się ruchem przyspieszonym to oznacza, że działające na niego siły NIE równoważą się!
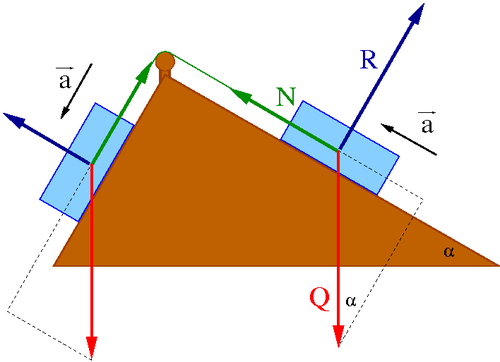
W przypadku ciała na równi:
- [math] R \; = \; Q \cdot \cos \alpha [/math]
- [math] N \; \ne \; Q \cdot \sin \alpha [/math]
Równowaga sił zachowana jedynie na kierunku prostopadłym do równi!
Równania ruchu
Podstawowym zagadnieniem dynamiki jest rozwiązywanie równań ruchu, czyli określanie ruchu ciała ze znajomości działających na nie sił.
Postać ogólna
Siła działająca na ciało może zależeć od położenia i prędkości ciała oraz czasu
- [math] \vec{F} \; = \; \vec{F}(\vec{r}, \vec{v}, t)[/math]
Podstawiając tą zależność do II zasady dynamiki otrzymujemy ogólną postać równania ruchu:
| [math]\displaystyle m \; \frac{d^2 \vec{r}(t)}{dt^2} \; = \; \vec{F}(\vec{r}, \vec{v}, t)[/math] |
Jest to w istocie układ trzech równań różniczkowych drugiego rzędu
- [math] m ( \frac{d^2 x}{dt^2} , \frac{d^2 y}{dt^2} , \frac{d^2 z}{dt^2}) \; = \; (F_x, F_y, F_z)[/math]
Ogólne rozwiązanie ma sześć stałych całkowania:
- [math] \vec{r} \; = \; \vec{r}\; (t,C_1, C_2, \ldots ,C_6)[/math]
Warunki początkowe
Aby ściśle określić ruch ciała musimy poza rozwiązaniem równań ruchu wyznaczyć wartości wolnych parametrów (w ogólnym przypadku sześciu)
Najczęściej dokonujemy tego określając warunki początkowe:
- [math] \vec{r}_0 \; = \; \vec{r}\; (t_0) [/math]
- [math] \vec{v}_0 \; = \; \vec{v}\; (t_0) [/math]
gdzie [math]t_0[/math] - wybrana "chwila początkowa"
W mechanice klasycznej obowiązuje
"zasada przyczynowości":
jeśli znamy równania ruchu oraz
dokładnie poznamy warunki
początkowe możemy jednoznacznie określić stan układu
w przeszłości i w
przyszłości.
Zachowanie obiektów mikroświata (np. cząstek elementarnych)
nie jest jednak deterministyczne.
Granice stosowalności mechaniki klasycznej określa wartość stałej Plancka [math] h=6.626\cdot 10^{-34}\; J \cdot s [/math]
Przykład
W ogólnym przypadku siła sprężysta może być przedstawiona w postaci:
- [math] \vec{F} \; = \; - k \; \vec{r}[/math]
Jest to więc siła centralna - działająca zawsze w kierunku środka układu (zawsze możemy tak wybrać), stara się przywrócić ciało do położenia równowagi.
Równanie ruchu sprowadza się do postaci:
- [math] \frac{d^2\vec{r}}{dt^2} \; = \; - \omega^2 \; \vec{r} \; , \qquad \qquad \omega = \sqrt{\frac{k}{m}} [/math]
⇒ oscylator harmoniczny.
Ogólne rozwiązanie równania ruchu:
- [math] \vec{r}(t) \; = \; \vec{A} \cdot \cos \omega t \; + \; \vec{B} \cdot \sin \omega t [/math]
Wartości [math]\vec{A}[/math] i [math]\vec{B}[/math] możemy wyznaczyć z warunków początkowych:
- [math]\vec{r}_0 = \vec{r}(0) \; = \; \vec{A} [/math]
- [math] \vec{v}_0 = \vec{v}(0) \; = \; \omega \vec{B} [/math]
- [math] \Rightarrow \; \vec{r}(t) \; = \; \vec{r}_0 \cdot \cos \omega t \; + \; \frac{\vec{v}_0}{\omega} \cdot \sin \omega t [/math]
Ruch jest płaski, odbywa się w płaszczyźnie wyznaczonej przez [math]\vec{r}_0[/math] i [math]\vec{v}_0[/math].
Torem ruchu w ogólnym przypadku jest elipsa.
W szczególnym przypadku torem ruchu może być:
- odcinek, jeśli [math]\vec{r}_0 || \vec{v}_0[/math] (albo [math]\vec{r}_0 = 0 [/math] albo [math]\vec{v}_0=0[/math])
- okrąg, jeśli [math]\vec{r}_0 \perp \vec{v}_0[/math] i [math]v_0 = \omega \cdot r_0[/math]
Więzy
Do tej pory rozważaliśmy ruch ciała, które może się
przemieszczać
bez ograniczeń w całej
trójwymiarowej przestrzeni - trzy stopnie swobody: [math]f[/math]=3.
W każdej chwili stan ciała opisuje sześć parametrów (dwa wektory: [math]\vec{r}[/math] i [math]\vec{v}[/math])
Powierzchnia więzów
W wielu przypadkach ruch ciała jest jednak ograniczony [math]\Rightarrow[/math] cząstka nieswobodna
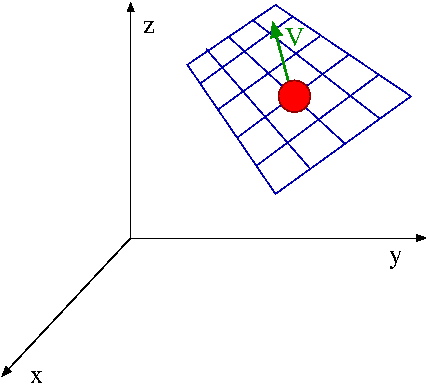
Ruch ciała może być na przykład ograniczony do zadanej powierzchni (np. powierzchnia stoku w przypadku narciarza, czy powierzchnia jeziora w przypadku łódki).
Ogólny warunek opisujący powierzchnie:
- [math] h(x,y,z,t) \; = \; 0 [/math]
Dodatkowy warunek powoduje, że zamiast trzech mamy dwa stopnie swobody [math]f[/math]=2
- ⇒ rozwiązanie równań ruchu ma cztery parametry początkowe
Krzywa więzów
Czasami ruch ciała jest ograniczony do zadanej krzywej w przestrzeni (np. wagon na torach, winda). Krzywą w przestrzeni możemy zawsze opisać porzez dwa warunki:
- [math] h_1(x,y,z,t) \; = \; 0 [/math]
- [math] h_2(x,y,z,t) \; = \; 0 [/math]
W zagadnieniu pozostaje więc jeden stopień swobody [math]f[/math]=1, a rozwiązanie równań ruchu ma dwa parametry początkowe.
Do równania ruchu musimy wprowadzić dodatkową siłę
reakcji więzów
| [math]\displaystyle m \; \frac{d^2 \vec{r}(t)}{dt^2} \; = \; \vec{F}(\vec{r}, \vec{v}, t) + \vec{F}_R[/math] |
gdzie:
- [math]\vec{F}(\vec{r}, \vec{v}, t)[/math] - siły zewnętrzne,
- [math]\vec{F}_R[/math] - reakcja więzów
Przy braku oporów ruchu (więzy idealne)
siła reakcji więzów jest zawsze prostopadła do powierzchni
lub krzywej więzów!
Więzy mogą być stacjonarne ( skleronomiczne), niezależne od czasu:
- [math] h(x,y,z) \; = \; 0 [/math]
lub zależne od czasu ( reonomiczne):
- [math]h(x,y,z,t)\;=\;0[/math]
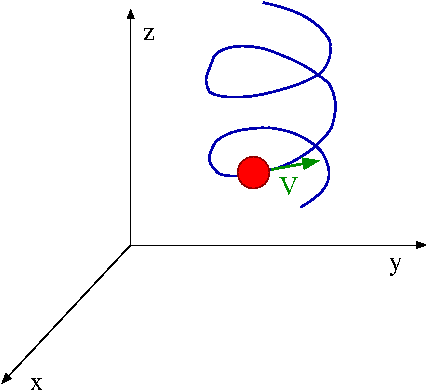
Przykład krzywej więzów: wahadło jednowymiarowe o długości l
Równania więzów:
- [math] l^2 - x^2 - y^2 - z^2 \; = \; 0[/math] - sfera
- [math] x \; = \; 0 [/math] - płaszczyzna
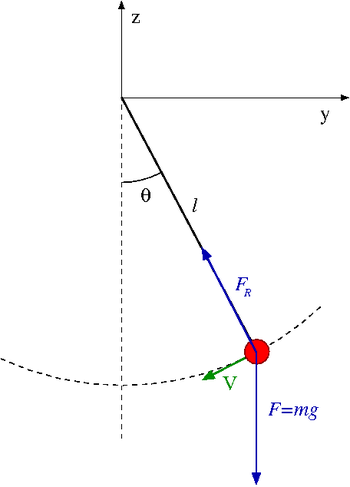
Wahadło
Warunki narzucone przez więzy najłatwiej uwzględnić opisując położenie kulki przez kąt [math]\Theta[/math]:
- [math] y = l \; \sin \Theta \; \; z = - l \; \cos \Theta [/math]
O sile reakcji [math]F_R(t)[/math] wiemy jedynie tyle, że działa wzdłuż nitki.
- [math] \frac{d^2y}{dt^2} = -\frac{F_R}{m} \sin \Theta \; \; \frac{d^2z}{dt^2} = -g + \frac{F_R}{m} \cos \Theta [/math]
Wynika z tego, że przyspieszenie styczne nie zależy od [math]F_R[/math]:
- [math] a_\Theta \equiv \cos \Theta \; \frac{d^2y}{dt^2} + \sin \Theta \; \frac{d^2z}{dt^2} \; = \; -g \cdot \sin \Theta [/math]
W przybliżeniu małych kątów ([math]\sin \theta \approx \theta[/math]) otrzymujemy więc:
- [math] l \; \frac{d^2\Theta}{dt^2} \; = \; -g \cdot \Theta [/math]
Jest to równanie oscylatora harmonicznego
- częstość wahań: [math]\omega = \sqrt{\frac{g}{l}}[/math],
- okres [math]T = 2 \pi \sqrt{\frac{l}{g}}[/math]
Rozwiązanie równania oscylatora harmonicznego:
- [math] \Theta(t) = \Theta_0 \cdot \cos (\omega t ) [/math]
Znając zależność wychylenia od czasu możemy wyznaczyć współrzędne:
- [math] y = l \; \sin \Theta \qquad z = - l \; \cos \Theta [/math]
Z kolei siłę reakcji możemy wyznaczyć z równania ruchu w [math]z[/math]:
- [math] \frac{dz}{dt} \; = \; l \sin \Theta \; \left[ - \Theta_0 \; \omega \sin ( \omega t) \right][/math]
- [math] \frac{d^2 z}{d t^2} \; = \; l \omega^2 \; \cos \Theta \; \left[ \Theta_0\; \sin (\omega t ) \right]^2 - l \omega^2 \sin \Theta \; \Theta_0\; \cos (\omega t )[/math]
Otrzymujemy:
- [math] F_R \; = \; \frac{m}{\cos \Theta} \left( \frac{d^2 z}{d t^2} + g \right) \; = \; mg \left[ \Theta_0^2 \; \sin^2 ( \omega t) - \tan \Theta \; \Theta_0\cos( \omega t) + \frac{1}{\cos\Theta} \right] [/math]
W przybliżeniu małych kątów: [math]\tan \Theta \approx \Theta[/math] i [math]\frac{1}{\cos\Theta} \approx 1 + \frac{1}{2}\Theta^2[/math]
- [math] F_R \; = \; mg \left[ \Theta_0^2 \; \sin^2 ( \omega t) - \frac{1}{2}\Theta_0^2 \; \cos^2 ( \omega t) + 1 \right] [/math]
Podstawiając zależność wychylenia [math]\Theta[/math] od czasu otrzymujemy ostatecznie:
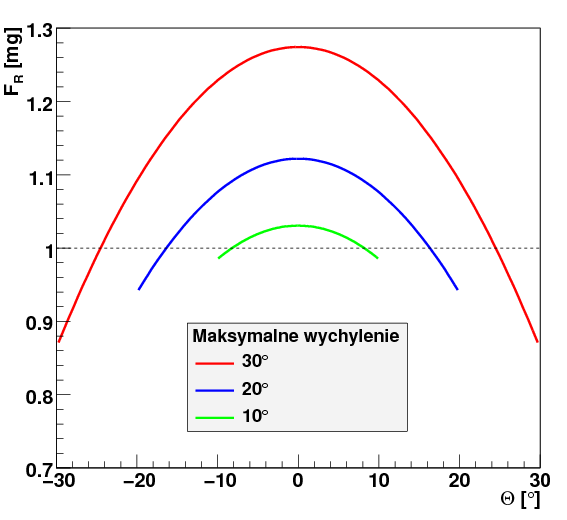
- [math] F_R(\Theta) \; = \; mg \left[ 1 + \Theta_0^2 - \frac{3}{2} \Theta^2(t) \right] [/math]
Uzyskana zależność przedstawiona jest poniżej dla kilku wybranych wartości wychylenia początkowego. Jak widać, naprężenie jest największe dla [math]\Theta=0[/math], w chwili przechodzenia wahadła przez położenie równowagi.