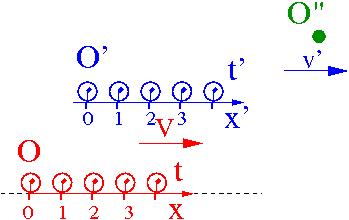FizykaI FMiN/Kinematyka relativity

Kinematyka relatywistyczna

Transformacja Lorentza

Ogólna postać transformacji

Transformacja Lorentza ma bardzo szczególne własności, nie jest "jednym z wielu" możliwych przekształceń. Korzystając tylko z:

• zasady bezwładności (definicji układu inercjalnego)
• zasady względności (równoprawności układów odniesienia)

można pokazać, że związek między współrzędnymi zdarzenia w dwóch układach odniesienia musi mieć postać:

[math] \left\{\begin{array}{lcl} t & = & \frac{t' \; + \; E\;V x'}{\sqrt{1 - E \; V^2}} \\[3mm] x & = & \frac{V t' \; + \; x'}{\sqrt{1 - E \; V^2}} \\[3mm] y & = & y' \\ z & =& z' \end{array}\right. [/math]

gdzie nieznana pozostaje jedynie stała [math]E[/math]

Transformacja Galileusza

Przyjęcie [math]E=0[/math] odpowiada transformacji Galileusza

[math] \left\{\begin{array}{ccl} t & = & t' \\ x & = & x' + V \; t' \\ y & = & y' \\ z & = & z' \end{array}\right. [/math]

albo (w zapisie macierzowym):

[math] \left(\begin{array}{r} c\;t \\ x \\ y \\ z \end{array}\right) \; = \; \left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ \beta & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} c\;t' \\ x' \\ y' \\ z'\end{array}\right) [/math]

gdzie [math]\beta = \frac{V}{c}[/math]

Konsekwencjami transformacji Galileusza jest:

• uniwersalność czasu
• względność prędkości [math]v = v' + V[/math]

W transformacji Galileusza czas jest wyróżniony! Nie ma symetrii między wymiarami przestrzennymi i czasem.

Transformacja Lorentza

Postulat Einsteina stałości prędkości światła oznacza przyjęcie [math]E = \frac{1}{c^2}[/math]. Wprowadzając tzw. czynnik Lorentza:

[math] \gamma = \frac{1}{\sqrt{1-E\; V^2}} \; = \; \frac{1}{\sqrt{1-\frac{V^2}{c^2}}} = \frac{1}{\sqrt{1-\beta^2}} [/math]

Otrzymujemy wzory na transformację Lorentza

[math] \left\{\begin{array}{rcc} ct & = & c \gamma t' \; + \; \gamma \beta x' \\ x & = & c \gamma \beta t' \; + \; \gamma x' \\ y & = & y' \\ z & = & z' \end{array}\right. [/math]

albo (w zapisie macierzowym):

[math] \left(\begin{array}{r} c \; t \\ x \\ y \\ z \end{array}\right) \; = \; \left(\begin{array}{cccc} \gamma & \gamma \; \beta & 0 & 0 \\ \gamma \; \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{r} c\; t' \\ x' \\ y' \\ z'\end{array}\right) [/math]

Pełna symetria między [math]ct[/math] (współrzędna czasową) i [math]x[/math] (współrzędną przestrzenną)!!!

Dla wygody często przyjmuje się konwencje [math]c\equiv 1 [/math] i pomija [math]c[/math] we wzorach.

Składanie prędkości

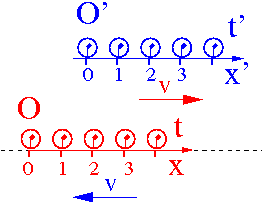
Rozważmy teraz ciało O", które w układzie O' porusza się z prędkością v' w kierunku osi x'.

[math]v' \; = \; \frac{x'}{t'}\;\;[/math] czyli [math]\;\; x' = v' \; t' [/math]

Jaką prędkość [math]v''[/math] ciała O" zmierzy obserwator O?

Dla ruchu jednostajnego możemy zapisać

[math] v'' \; = \; \frac{x}{t}[/math]

Podstawiając wyrażenia na [math]x[/math] i [math]t[/math] z transformacji Lorentza dostajemyL

[math] v'' \; = \; \frac{\gamma \; x'+ \gamma \beta \;ct'} {\gamma \;t'+ \frac{\gamma \beta}{c} \;x'} \; = \; \frac{\gamma \; v't'+ \gamma \beta \;c \; t'} {\gamma \; t'+ \frac{\gamma \beta}{c} v'\; t'} [/math]

Ostatecznie otrzymujemy:

[math] v'' \; = \; \frac{V + v'}{1 \; + \; \frac{V v'}{c^2}} [/math]

lub, dla prędkości wyrażonych w jednostkach prędkości światła

[math] \beta'' \; = \; \frac{\beta + \beta'}{1 \; + \; \beta \beta'} \qquad \; \ne \; \beta + \beta' [/math]

W podejściu Einsteina składanie prędkości nie polega na ich prostym dodawaniu.

W szczególności prędkość światła pozostaje stała ([math]\beta'=1 \; \Rightarrow \; \beta''=1[/math]) niezależnie od układu odniesienia.

Transformacja Lorentza przechodzi w transformację Galileusza w granicy [math]\frac{1}{c^2} \rightarrow 0[/math]

Uogólnienie

Wyrażenia na Transformację Lorentza uzyskaliśmy przy założeniu, że początki układów mijają się w chwili [math]t=t'=0[/math]. Zdarzenie to ma w obu układach współrzędne [math](0,0,0,0)[/math]. Jest to więc wspólne zdarzenie odniesienia

W ogólności Transformację Lorentza opisuje transformację różnicy współrzędnych dwóch wybranych zdarzeń A i B: [math]\Delta t = t_B - t_A, \;\; \Delta x = x_B - x_A \;...[/math]

Przyjmując [math]c \equiv 1[/math]:

[math] \left(\begin{array}{c} \Delta t \\ \Delta x \\ \Delta y \\ \Delta z \end{array}\right) \; = \; \left(\begin{array}{c} \gamma \; \Delta t' \; + \; \gamma \; \beta \; \Delta x' \\ \gamma \; \beta \; \Delta t' \; + \; \gamma \; \Delta x' \\ \Delta y' \\ \Delta z' \end{array}\right) \; = \; \left(\begin{array}{cccc} \gamma & \gamma \; \beta & 0 & 0 \\ \gamma \; \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} \Delta t' \\ \Delta x' \\ \Delta y' \\ \Delta z'\end{array}\right)[/math]

Jeśli przyjmiemy, że w obu układach [math]A = (0,0,0,0)[/math] to otrzymamy jak poprzenio transformację współrzędnych zdarzenia B.

Wykres Minkowskiego

Przedstawienie osi czasu

Niech zegar referencyjny w układzie O' błyska z upływem każdej jednostki czasu. Zdarzenia temają współrzędne:

[math] ct' \; = \; i \cdot \Delta c t' \; = \; i [/math]

[math] x' \; = \; 0 \qquad\qquad i=0, 1, \ldots [/math]

Z transformacji Lorentza uzyskujemy współrzędne tych zdarzeń w układzie O:

[math] ct \; = \; i \cdot \gamma \Delta ct' \; = \; i \cdot \gamma [/math]

[math] x \; = \; i \cdot \gamma \beta \Delta ct' \; = \; i \cdot \gamma \beta [/math]

Zdarzenia te leżą na lini świata ciała O', a jednocześnie pokazują nam upływ czasu w jego układzie odniesienia. Tym samym "tyknięcia" te obrazują nam oś ct'.

Przedstawienie współrzędnej przestrzennej

Niech zegary rozmieszczone wzdłuż osi x' układu O' wyślą w tej samej chwili t'=0 błysk światła. W O' zdarzenia te mają współrzędne:

[math] ct' \; = \; 0 [/math]

[math] x' \; = \; i \cdot \Delta x' \; = \; i [/math]

Z transformacji Lorentza uzyskujemy współrzędne tych zdarzeń w układzie O:

[math] ct \; = \; i \cdot\gamma \beta \Delta x' \; = \; i \cdot \gamma \beta [/math]

[math] x \; = \; i \cdot \gamma \Delta x' \; = \; i \cdot \gamma [/math]

Zdarzenia te pokazują nam jak w układzie O wyglądają zdarzenia równoczesne w O', odwzorowują nam też jednostkę długości. Możemy traktować to jako obraz ośi x'.

Konstrukcja wykresu Minkowskiego

Osie układu O' rysujemy jako nachylone do osi układu O pod kątem

[math] \tan \theta \; = \; \beta \; = \; \frac{V}{c} [/math]

Przy czym odkładane wzdłuż osi układu O' jednostki są wydłużone. Widziane w układzie O jednostki osi O' wynoszą:

[math] 1' \; = \; \gamma[/math]

Transformacja odwrotna

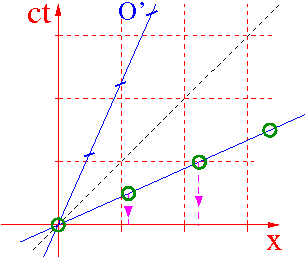
Wykres Minkowskiego możemy także narysować z punktu widzenia obserwatora O'. Odpowiada on wtedy odwrotnej transformacji Lorentza.

Sytuacja jest w pełni symetryczna, także obserwator O' widzi wydłużenie osi układu O!

Obaj obserwatorzy stwierdzą wydłużenie jednostek w poruszającym się układzie.

Wybierając zgodne zwroty osi układów naruszyliśmy symetrie: układ O porusza się w kierunku przeciwnym do zwrotu osi x', a O' zgodnie z x. Dlatego wykresy nie wyglądają identycznie.

Interpretacja

Transformacje Lorentza możemy też zapisać jako "hiper obrót" w czasoprzestrzeni:

[math] \left(\begin{array}{r} c \; t \\ x \\ y \\ z \end{array}\right) \; = \; \left(\begin{array}{cccc} \cosh \eta & \sinh \eta & 0 & 0 \\ \sinh \eta & \cosh \eta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot \left(\begin{array}{c} c\; t' \\ x' \\ y' \\ z' \end{array}\right) [/math]

gdzie [math]\eta[/math] jest parametrem transformacji, a [math]\cosh[/math] i [math]\sinh[/math] to tzw. funkcje hiperboliczne.

Parametr transformacji jest zdefiniowany zależnością

[math] \eta \; = \; \ln \left[ \gamma ( 1 + \beta ) \right] \; = \; \ln \left( \sqrt{\frac{1+\beta}{1-\beta}} \right) \; = \; \frac{1}{2} \ln \frac{1+\beta}{1-\beta}[/math]

Znając [math]\eta[/math] możemy wyznaczyć [math]\beta[/math] z zależności

[math] \beta \; = \; \tanh \eta \; = \; \frac{\sinh \eta}{\cosh \eta } [/math]

Okazuje się, że składanie transformacji Lorentza w tej formie sprowadza się do dodawanie (!) współczynników transformacji (tak jak w przypadku kątów obrotu). Dlatego też współczynnik [math]\eta[/math] nazywany jest kątem hiperbolicznym.

Funkcje hiperboliczne można zdefiniować wzorami:

[math] \sinh x \; = \; \frac{e^x - e^{-x}}{2} [/math]

[math] \cosh x \; = \; \frac{e^x + e^{-x}}{2} [/math]

przy czym obowiązuje tożsamość

[math] \cosh^2 x \; - \; \sinh^2 x \; = \; 1 [/math]

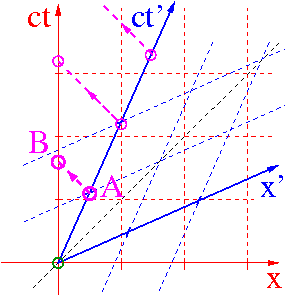
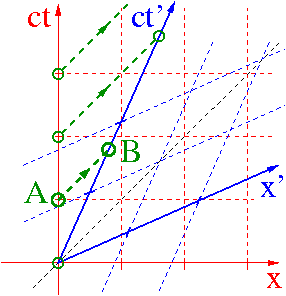
Dylatacja czasu

Prezentacja graficzne

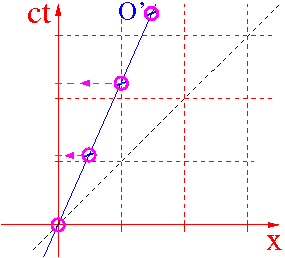
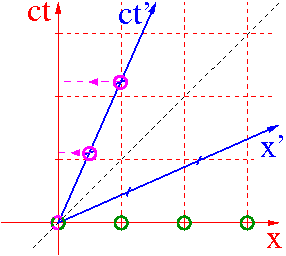
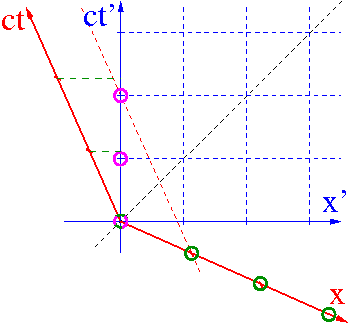
Zegar układu O' jest obserwowany z ukladu O. Rejestrowane są współrzędne czasowe i przestrzenne jego kolejnych "tyknięć".

Problem nie jest symetryczny: zegar spoczywa w O', obserwator O porównuje jego wskazania z różnymi zegarami swojej siatki

Obserwator O stwierdzi, że zegar w O' chodzi wolniej:

[math]\Delta t = \gamma \cdot \Delta t'[/math]

Obserwator O' stwierdzi, że pomiar obserwatora O był źle wykonany, bo zegary w O

• nie są zsynchronizowane,
• chodzą za wolno.

Pomiar

W roku 1972 przeprowadzono eksperyment z zegarami atomowymi, które wysłano w podróż samolotem dookoła świata (Hafele i Keating, 1972). Przy rozważanych prędkościach porównywalny jest wpływ oddziaływań grawitacyjnych (opisanych przez Ogólną Teorię Względności).

Przewidywane różnice czasu (w porównaniu z nieruchomym zegarem):

Przewidywania [ns]	Lot na wschód	Lot na zachód
efekt kinematyczny	-184 [math]\pm[/math] 18	96 [math]\pm[/math] 10
efekt grawitacyjny	144 [math]\pm[/math] 14	179 [math]\pm[/math] 18
suma	-40 [math]\pm[/math] 23	275 [math]\pm[/math] 21

Uzyskane wyniki doświadczalne

Pomiar [ns]	Lot na wschód	Lot na zachód
zegar 1	-57	277
zegar 2	-74	284
zegar 3	-55	266
zegar 4	-51	266
Średnia	-59 [math]\pm[/math] 10	273 [math]\pm[/math] 7

Czas życia cząstek

Z istotnym wpływem dylatacji czasu mamy w fizyce cząstek elementarnych. Cząstkami, które stanowią większość tzw. wtórnego promieniowania kosmicznego przy powierzchni Ziemi sa miony.

Średni czas życia mionu w spoczynku to

[math]\tau[/math] = 2.2 [math]\mu[/math]s

Gdyby nie było dylatacji czasu to nawet poruszając się z prędkością światła miony pokonywałyby średnio jedynie

[math]\langle l \rangle \; = \; \beta c \tau \; \le [/math] 659m

Miony produkowane w górnych warstwach atmosfery, na wysokości powyżej 10km. Gdyby nie było dylatacji czasu nie miałyby szans dotrzeć do Ziemi. Produkowane w oddziaływanich pierwotnego promieniowania kosmicznego miony mają jednak bardzo duże energie, [math]\langle E \rangle \sim[/math] 3 GeV, a w związku z tym poruszają się z prędkościami bardzo bliskimi prędkości światła

[math]\gamma \sim 30[/math].

Dla tego bez problemu docierają do powierzni Ziemi:

[math]\beta \gamma c \tau \sim[/math] 20km

Interwał czasoprzestrzenny

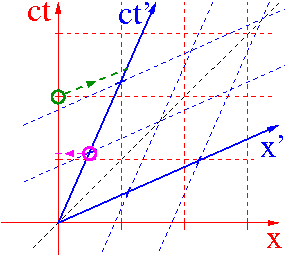
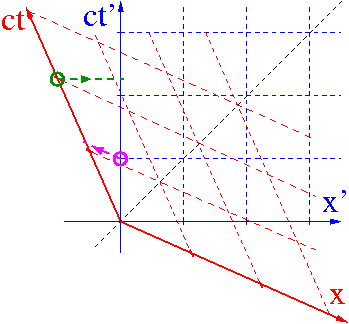
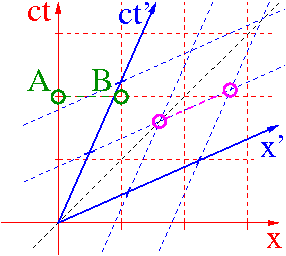
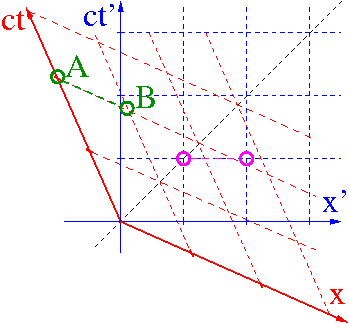
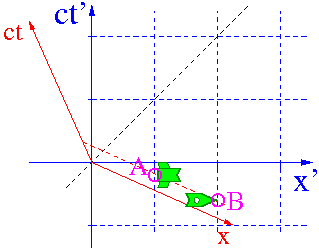
Względność równoczesności

Dwa zdarzenia równoczesne w układzie O nie są równoczesne w układzie O'.

Kolejność w jakiej zaobserwuje je obserwator O' zależy od położenia zdarzeń w stosunku do kierunku ruchu względnego.

Interwał

Interwał czasoprzestrzenny między dwoma zdarzeniami definiujemy jako:

[math] s_{AB} \; = \; (\Delta c t)^2 - (\Delta x)^2 - (\Delta y)^2 - (\Delta z)^2 [/math]

Interwał jest niezmiennikiem transformacji Lorentza ! Można go traktować jako "odległość" w czasoprzestrzeni. Nie zależy od układu odniesienia, w którym go mierzymy.

Przyczynowość

Jeśli interwał czasoprzestrzenny między dwoma zdarzeniami A i B [math]s_{AB} \gt 0[/math] to można znaleźć taki układ odniesienia, w którym zdarzenia A i B będą zachodzić w tym samym miejscu. O takim interwale mówimy, że jest czasopodobny (typu czasowego).

[math]\sqrt{s_{AB}}[/math] określa wtedy odstęp czasu między zdarzeniami w tym układzie.

Jeśli zdarzenia A i B związane są z ruchem jakiejś cząstki (należą do jej lini świata) mówimy, że jest to czas własny tej cząstki.

Jeśli interwał jest czasopodobny to zdarzenia A i B mogą być powiązane przyczynowo. Ich kolejność jest zawsze ta sama.

Jeśli [math]s_{AB} \lt 0[/math] to można znaleźć taki układ odniesienia, w którym zdarzenia A i B będą zachodzić w tej samej chwili. O takim interwale mówimy, że jest przestrzeniopodobny (typu przestrzennego).

[math]\sqrt{-s_{AB}}[/math] określa odległość przestrzenną między zdarzeniami w tym układzie.

Jeśli interwał jest przestrzeniopodobny, zdarzenia A i B NIE mogą być powiązane przyczynowo ! Kolejność zdarzeń zależy od układu odniesienia.

Jeśli interwał [math]s_{AB} = 0[/math] to w żadnym układzie odniesienia zdarzenia A i B nie będą zachodzić w tej samej chwili ani w tym samym miejscu

O takim interwale mówimy, że jest to interwał zerowy

Zdarzenia A i B może połączyć przyczynowo jedynie impuls świetlny

Podsumowując:

• [math]s_{AB} \gt 0[/math] - interwał czasopodobny
• [math]s_{AB} \lt 0[/math] - interwał przestrzeniopodobny
• [math]s_{AB} = 0[/math] - interwał zerowy

Jeśli przyjmiemy, że zdarzenie O ma miejsce "tu i teraz" i [math]t_0 = 0[/math], wtedy możemy każde inne zdarzenie A przyporządkować do jednej z 3 kategorii:

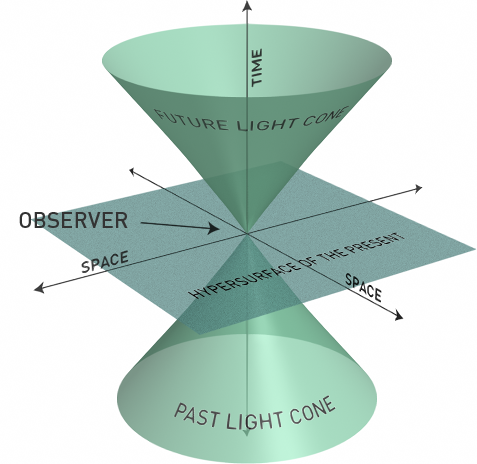
• bezwzględna przyszłość: zdarzenia na które możemy mieś wpływ, to zdarzenia dla których

[math]s_{OA} \gt 0[/math] i [math]t_A \gt 0[/math]

na rysunku poniżej zawarte wewnątrz górnego stożka

• bezwzględna przeszłość: zdarzenia które mogły mieś wpływ na nas

[math]s_{OA} \gt 0[/math] i [math]t_A \lt 0[/math]

na rysunku poniżej zawarte wewnątrz dolnego stożka

• zdarzenia bez związku przyczynowego

[math]s_{OA} \lt 0[/math]

obejmują obszar na zewnątrz obu stożków

Skrócenie Lorentza

Pomiar długości

Rozważmy rakietę o długości [math]L_0[/math] poruszającą się w dodatnim kierunku osi X układu O. Niech O' będzie układem związanym z rakietą.

Jaką długość rakiety zmierzy obserwator w układzie O?

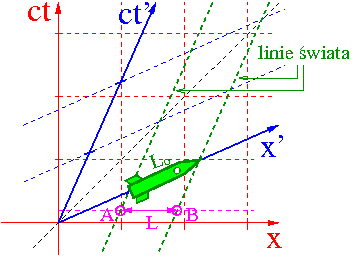
Pomiar długości to równoczesny pomiar położenia obu końców. Oznaczmy te pomiary jako zdarzenia A i B.

Pomiar odległości między zdarzeniami AB w układzie O:

[math] \Delta x_{AB} \; = \; L [/math]

[math] \Delta t_{AB} \; \equiv \; 0 [/math] (!)

W układzie O' odległość między zdarzeniami A i B jest z definicji równa długości rakiety (nawet jeśli zdarzenia nie są równoczesne - rakieta spoczywa w tym układzie)

[math] L_0 \; \equiv \; \Delta x_{AB}' \; = \; \gamma \; \Delta x_{AB} \; = \; \gamma \; L[/math]

Otrzymujemy:

[math] \Rightarrow \;\;\; L \; = \; \frac{1}{\gamma} \; L_0 [/math]

Obserwator w układzie O zmierzy mniejszą długość niż długość mierzona w układzie własnym rakiety - skrócenie Lorentza

Skrócenie Lorentza ma związek ze względnością równoczesności. Obserwator O uważa, że równocześnie zmierzył położenie obu końców rakiety (zdarzenia A i B).

Obserwator O' stwierdzi, że pomiary A i B nie były równoczesne, [math]\Delta t_{AB}' \ne 0 [/math]! Wcześniej zmierzono położenie przodu niż tyłu rakiety. W tym czasie rakieta przesunęła się i to tłumaczy zły pomiar.

Paradoks "tyczki w stodole"

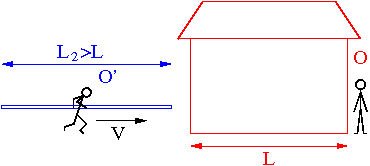
Rozważmy biegacza O', który wbiega do stodoły o długości [math]L[/math] z tyczką o długości [math]L_2[/math].

Obserwator O powie, że tyczka się skóciła i zmieściła w stodole. (zakładając, że [math]\frac{L_2}{\gamma} \lt L[/math]).

Natomiast biegacz O' stwierdzi, że to stodoła się skróciła. Tyczka nie mogła się w niej zmieścić.

Obaj mają rację !!!

Różni ich zdanie na temat kolejności zdarzeń: minięcia wrót stodoły przez końce tyczki. Zdarzenia te są rozdzielone przestrzennie ([math]s \lt 0[/math]) więc kolejność zależy od układu odniesienia.

Dla obserwatora O koniec tyczki najpierw minie pierwsze drzwi stodoły, a dopiero potem początek tyczki uderzy w drugie drzwi.

Dla obserwatora O' najpierw początek tyczki uderzy w drugie drzwi, a dopiero potem koniec tyczki minie pierwsze drzwi stodoły. Tyczka nie może wcześniej się zatrzymać - między tymi zdarzeniami nie ma związku przyczynowego.

Paradoks bliźniąt

Paradoks

Kosmonauta wyrusza w podróż na [math]\alpha \; Cen[/math], jego brat bliźniak zostaje na Ziemi. Obaj bracia - obserwatorzy mierzą czas pomiędzy dwoma zdarzeniami:

• wylotem rakiety
• powrotem na Ziemię

Poruszając się względem siebie z prędkością porównywalną z prędkością światła każdy z nich stwierdzi, że jego brat powinien być młodszy, zgodnie z formułą na dylatację czasu. Obaj nie mogą mieć racji...

Ale dla obu z nich oba zdarzenia zaszły też w tym samym miejscu. Może powinni być w tym samym wieku (z niezmienniczości interwału)?!

Jak rozstrzygnąc czy i który z braci będzie młodszy?

Przyjmijmy, że podróż odbywa się z prędkością [math]v = 0.745 \;c[/math] ([math]\gamma = 1.5[/math]). Według obserwatora na Ziemi podróż zajmie

[math]t_Z = \frac{2 \times 4.3}{0.745} \;\approx\; 11.5 ~lat[/math]

Dzięki dylatacji czasu, mierzony przez kosmonautę czas podróży skróci się do:

[math]t_K = \frac{11.5 lat}{1.5} \;\approx \;7.7 ~lat[/math]

Dla kosmonauty odległość, którą musi przebyć skróci się do [math]\displaystyle \frac{4.3}{1.5} \approx 2.9 [/math] lat świetlnych (skrócenie Lorentza). Podróż będzie jego zdaniem trwała

[math]t_K = \frac{2 \times 2.9}{0.745} \approx 7.7[/math] lat

to samo powiedział jego brat...

Ale dla kosmonauty bieg zegarów na Ziemi ulega spowolnieniu (dylatacja czasu). Jego zdaniem, w czasie jego lotu do układu [math]\alpha[/math]-Centaura na Ziemi mija tylko

[math]\frac{0.5 \times 7.7 lat}{1.5} \approx 2.6[/math] lat

Tyle samo czasu mija na Ziemi w czasie jego podróży powrotnej. Łącznie w trakcie całej podróży powinno minąć

[math]t'_Z = \frac{7.7 lat}{1.5} \approx 5.1[/math] lat

Ale brat na Ziemi stwierdzi, że minęło 11.5 lat

Gdzie znika ponad 6 lat !?

Układy odniesienia

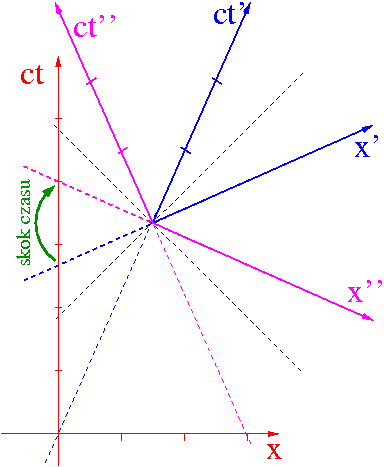
Istotne dla zrozumienia tego paradoksu jest zauważenie, że mamy tu do czynienia z trzema (a nie dwoma) układami odniesienia:

• układ O związany z Ziemią
• układ O' związany z rakietą w trakcie jej podróży do [math]\alpha \; Cen[/math]
• układ O" związany z rakietą w trakcie podróży powrotnej

Kosmonauta obserwuje wskazania zegara na Ziemi najpierw w układzie O', a po zawróceniu w układzie O". Na zegarze tym przybywa "skokowo" ponad 6 lat w momencie zmiany przez kosmonautę układu współrzędnych.

Zegar na Ziemi nie może być wprost porównywany z zegarem referencyjnym kosmonauty, zawsze porównywany jest z najbliższym zegarem układu współporuszającego się. Kluczowa jest synchronizacja zegarów, która zmienia się przy zmianie układu odniesienia.

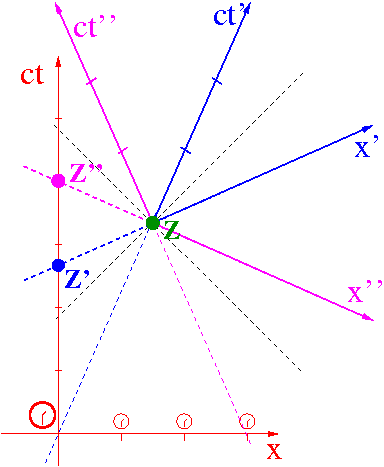
Kosmonauta obserwuje wskazania zegara na Ziemi porównując go zawsze z najbliższym zegarem jego układu:

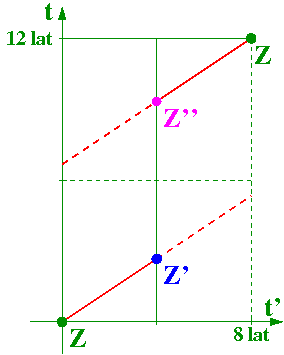
• w chwili startu ([math]t=t'=0[/math]) jest to jego własny zegar Z.
• tuż przed dotarciem do celu jest to zegar Z' z układu O'
• tuż po zawróceniu jest to zegar Z" z układu O".

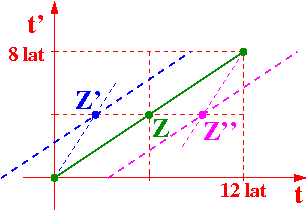
Także obserwator na Ziemi może obserwować wskazania zegarów kosmonauty ( Z, Z' i Z") porównując je ze swoją siatką zegarów.

Obserwacje kosmonauty

Czas na Ziemi według kosmonauty

Dolatując do celu, po [math]t' \sim 4[/math] latach (według swojego zegara Z), kosmonauta stwierdza, że na Ziemi mineło [math]t \lt 3[/math] lata.

Kosmonauta opiera się na wskazaniach zegara Z' zsynchronizowanego z Z.

Po zawróceniu informacja o wskazaniach zegara na Ziemi pochodzi od zegara Z", też zsynchronizowanego z Z ale w nowym układzie odniesienia.

Według zegara Z" w chwili zawracania zegar na Ziemi wskazywał [math]t \gt 9[/math] lat.

Obserwacje ziemianina

Wskazania zegarów kosmonauty rejestrowane przez obserwatora na Ziemi

Według obserwatora na Ziemi bieg zegara Z kosmonauty jest spowolniony na skutek dylatacji czasu.

Kosmonauta źle ocenił bieg czasu na Ziemi gdyż:

• najpierw użył zegara Z', który spieszył się względem Z
• potem użył zegara Z", który spóźniał się względem Z

Według obserwatora nia Ziemi, zawrócenie rakiety Z, oraz zdarzenia porównania czasu na Ziemi z przelatującymi zegarami Z' i Z" nie były równoczesne.

W chwili zawracania zegar Z' dawno minął Ziemię, a zegar Z" jeszcze do niej nie doleciał.

Dokonany przez kosmonautę pomiar czasu jaki upłynął na Ziemi jest nieprawidłowy, ze względu na zmianę układu odniesienia.

Na ziemi minęło 11.5 lat.

Obaj obserwatorzy zgadzają się, że dla kosmonauty minęło 7.7 lat.

Efekt Dopplera

Przypadek klasyczny

W klasycznym zagadnieniu efektu Doppleta dla dźwięku rozważaliśmy dwa przypadki:

Ruchome źródło

Częstość dźwięku i długość fali mierzone przez obserwatora nieruchomego względem ośrodka wynoszą

[math] f' = \frac{f}{1+\beta} [/math]

[math] \lambda ' = \lambda \; \left( 1+ \beta \right) [/math]

Ruchomy obserwator

Częstość i długość fali emitowanej przez nieruchome względem ośrodka źródło, mierzone przez ruchomego obserwatora wynoszą

[math] f' = f \; \left(1-\beta\right) [/math]

[math] \lambda ' = \frac{\lambda}{ 1- \beta } [/math]

W przypadku dźwięku efekt zależy nie tylko od względnego ruchu źródła i obserwatora, ale także od ruchu względem ośrodka.

Ale światło nie potrzebuje "ośrodka". Powinien się liczyć tylko ruch względny !...

Przypadek relatywistyczny

Jeśli źródło i/lub obserwator poruszają się z dużymi prędkościami należy uwzględnić dylatację czasu!

Jest ona dana przez współczynnik Lorentza

[math]\displaystyle \gamma = \frac{1}{\sqrt{1-\beta^2}} = \frac{1}{\sqrt{(1-\beta)(1+\beta)}}[/math]

Ruchome źródło

Poruszające się źródło drga (z punktu widzenia obserwatora) z częstością [math]\gamma[/math] razy mniejszą:

[math] f' \; = \; \frac{f / \gamma }{1+\beta} \; = \; f \; \sqrt{\frac{1-\beta}{1+\beta}} [/math]

Ruchomy obserwator

Zegar poruszającego się obserwatora chodzi wolniej, mierzona przez niego częstość jest więc [math]\gamma[/math] razy większa:

[math] f' \; = \; \gamma \; f \; \left(1-\beta \right) = \; f \; \sqrt{\frac{1-\beta}{1+\beta}} [/math]

Widzimy, że w przypadku relatywistycznym oczekiwana zmiana częstości nie zależy od wyboru układu odniesienia. Pełna symetria !

Przedstawienie graficzne

Ruch źródła

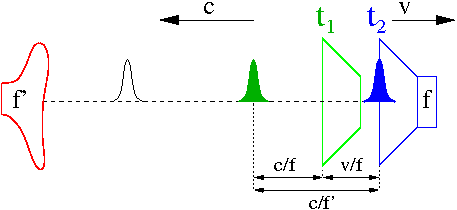
Wysłanie impulsu w układzie O':

[math]A \; : \; (T,0,0,0)[/math]

W układzie O ([math]c=1[/math])

[math]A \; : \; (\gamma \; T, \beta \gamma \; T ,0,0)[/math]

Na pokonianie odległości [math]\beta \gamma T[/math] światło potrzebuje [math]\beta \gamma \; T[/math] czasu. Dotarcie impulsu światła do obserwatora O:

[math]B \; : \; (\gamma \; T + \beta \gamma \; T ,0 ,0,0)[/math]

Mierzony przez O czas dotarcia impulsu to wyznaczony okres drgań

[math] T' \; = \; \gamma (1 + \beta) \; T = \sqrt{\frac{1+\beta}{1-\beta}} \; T [/math]

Ruch obserwatora

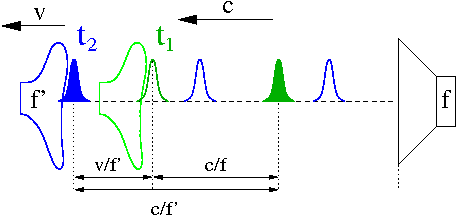
Wysłanie impulsu w układzie O:

[math]A \; : \; (T,0,0,0)[/math]

Dotarcie impulsu do obserwatora O':

[math]B \; : \; (T+\Delta T ,\Delta T ,0,0)[/math]

Opóźnienie w odebraniu impulsu możemy wyznaczyć zapisując prędkość O' względem O:

[math]\displaystyle \beta = \frac{\Delta T}{T + \Delta T}[/math]

i odwracając tą zależność:

[math]\displaystyle \Delta T = \frac{\beta}{1-\beta} \; T [/math]

Współrzędne dotarcia impulsu w O wynoszą więc:

[math] B \; : \; (\frac{T}{1 - \beta} ,\frac{\beta \; T}{1 - \beta} ,0,0)[/math]

Według O' (dylatacja czasu)

[math]B \; : \; (\frac{T}{\gamma ( 1 - \beta) } ,0,0,0) [/math]

Mierzony przez O' czas dotarcia impulsu to wyznaczony okres drgań [math] T' \; = \; \frac{ T }{\gamma ( 1 - \beta) } = \sqrt{\frac{1+\beta}{1-\beta}} \; T [/math]

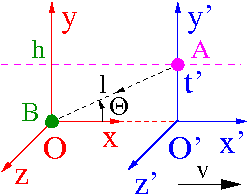
Przypadek ogólny

Niech źródło światła przelatuje w odległości h od obserwatora znajdującego się w początku układu O:

Przyjmijmy, że w chwili [math]t[/math], mierzonej w układzie O', wysłany zostaje impuls świetlny w kierunku obserwatora

[math]A \; : \; (t,0,h,0)[/math]

Współrzędne tego zdarzenia w układzie O (z transformacji Lorentza):

[math]A \; : \; (\gamma \; t,\gamma \beta \; t,h,0)[/math]

Możemy teraz policzyć czas dotarcia impulsu do obserwatora O (zdarzenie B):

[math] t' \; = \; \gamma t + l \; = \; \gamma t + \sqrt{ (\gamma \beta t )^2 + h^2}[/math]

Współczynnik przesunięcia dopplerowskiego możemy policzyć z różnicy [math]dt'[/math] między czasami dotarcia dwóch impulsów wysłanych w odstępie czasu [math]dt[/math]:

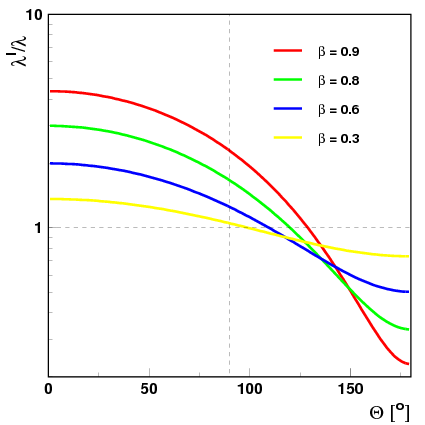
[math] \frac{\lambda ' }{\lambda} = \frac{dt'}{dt} \; = \; \gamma + \frac{\gamma^2 \beta^2 t}{ \sqrt{ (\gamma \beta t )^2 + h^2}} \; = \; \gamma \left( 1 + \beta \; \frac{x}{l} \right) \; = \; \gamma \left( 1 + \beta \; \cos\Theta \right) [/math]

gdzie: [math]\lambda[/math] - emitowana długość fali (w układzie źródła), [math]\lambda'[/math] - mierzona długość fali, a [math]\Theta[/math] to kąt obserwacji (kąt z jakiego według obserwatora O nadlatuje impuls światła).

Przesunięcie długości fali obserwujemy także dla [math]\Theta = 90^\circ[/math] !!!

Klasycznie nie ma w tym przypadku zmiany częstości...

Prawo Hubbla

Efekt Dopplera obserwowany w warunkach laboratoryjnych dla dla fal elektromagnetycznych jest na ogól bardzo niewielki (z wyjątkiem akceleratorów cząstek i ciężkich jonów).

Duże efekty widoczne są natomiast w obserwacjach astronomicznych

W widmie światla emitowanego przez wzbudzone atomy widoczne są charakterystyczne linie widmowe, są to tzw. Linie emisyjne. Częściej jednak obserwujemy tzw. linie absorpcyjne widoczne w świetle przechodzącym przez gaz pochłaniający fale odpowiadające jego charakterystycznym liniom widmowym.

W obu przypadkach pozycja linii jest ściśle określona (dla danego atomu)

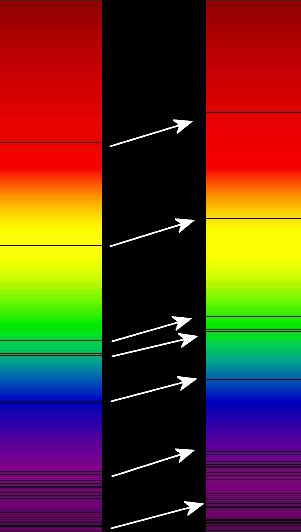
Mierząc linie absorpcyjne w widmie galaktyk możemy wnioskować o ich ruchu i wyznaczyć ich prędkość względem nas. Na rysunku poniżej linie absorpcyjne w widmie odległej supergromady galaktyk (BAS11) (po prawej stronie) porównane są z liniami w widmie słonecznym (po lewej stronie).

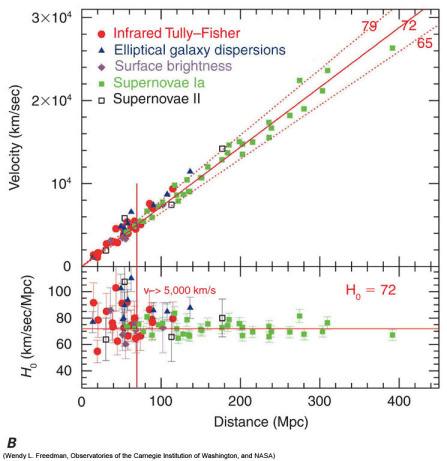
Dzięki efektowi Dopplera wiemy, że Wszechświat się rozszerza. W 1929 roku Edwin Hubble jako pierwszy powiązał obserwowane prędkości mgławic z ich odległością od Ziemi. Zauważył on, że prędkość 'ucieczki' rośnie z odległością od Ziemi:

[math] v \; = \; H \cdot r [/math]

gdzie [math]r[/math] - odległość obiektu od Ziemi, a [math]H[/math] - stała Hubbla.

Obecne pomiary dają wartość [math]H \sim 72 \; km/s/Mpc[/math] ( [math]1 Mpc \approx 3 \cdot 10^{22} m [/math]).