Fizyka III/Drgania układów o wielu stopniach swobody

Wstęp

W przypadku drgań układów o wielu stopniach swobody będziemy korzystać z zasady superpozycji, którą na nasze potrzeby możemy sformułować następująco:

1. Równania liniowe jednorodne. Suma dwóch dowolnych rozwiązań równania liniowego jednorodnego jest również rozwiązaniem tego równania.
2. Równania liniowe niejednorodne. Jeśli działanie siły [math]F_1[/math] wywołuje drgania [math]x_1[/math], a działanie siły [math]F_2[/math] wywołuje drganie [math]x_2[/math], to jednoczesne działanie sił [math]F_1 +F_2[/math] wywołuje drgania [math]x_1+x_2[/math].
3. Ruch układu o dwóch stopniach swobody, opisany równaniami liniowymi stanowi superpozycję dwóch niezależnych jednoczesnych ruchów harmonicznych. Ruchy te nazywamy ruchami (drganiami) normalnymi lub drganiami własnymi danego układu. Dobierając odpowiednio warunki początkowe możemy wzbudzić wybrane drgania własne. Jeśli układ wykonuje drgania własne, to każdy element układu drga z tą samą częstotliwością (własną) i z taką samą fazą.

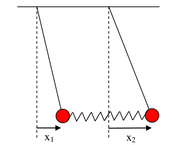
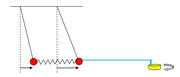
Taką “wiedzę” przekazuje nam matematyka. Teraz zastosujmy ją do fizyki. Jako przykład będziemy rozważać dwa wahadła proste o długości l i masie m sprzężone za pomocą sprężyny o stałej sprężystości k. Odległość zawieszenia obu wahadeł równa się długości swobodnej sprężyny (patrz rysunek Figure 1).

Dwa wahadła proste sprzężone za pomocą sprężyny.

Wychylenie z położenia równowagi pierwszego wahadła oznaczamy [math]x_1[/math] a drugiego [math]x_2[/math]. W przybliżeniu małych drgań otrzymujemy dwa równania opisujące rozpatrywany układ wahadeł:

[math]m\frac{\mathrm d x_1}{\mathrm dt^2}=-\frac{mg}lx_1+k(x_2-x_1)[/math]

[math]m\frac{\mathrm d x_2}{\mathrm dt^2}=-\frac{mg}lx_2-k(x_2-x_1)[/math]

Układ równań możemy przekształcić dodając je i odejmując stronami:

[math]m\left( \frac{\mathrm d x_1}{\mathrm dt^2}+\frac{\mathrm d x_2}{\mathrm dt^2}\right)=-\frac{mg}l(x_1+x_2)[/math]

[math]m\left( \frac{\mathrm d x_1}{\mathrm dt^2}-\frac{\mathrm d x_2}{\mathrm dt^2}\right)=-\frac{mg}l(x_1-x_2)-2k(x_1-x_2)[/math]

Jeśli wprowadzimy podstawienia: [math]z_1=x_1+x_2[/math] i [math]z_2=x_1-x_2[/math], to otrzymamy dwa równania oscylatora harmonicznego:

[math]m\frac{\mathrm d z_1}{\mathrm dt^2}+\frac{mg}lz_1=0[/math]

[math]m\frac{\mathrm d z_2}{\mathrm dt^2}+\left(\frac{mg}l+2k\right) z_2=0[/math]

których rozwiązania są nam dobrze znane:

[math]z_1=A_1\cos(\omega_1 t+\phi_1)[/math]

[math]z_2=A_2\cos(\omega_2 t+\phi_2)[/math]

gdzie:

[math]\omega_1^2=\frac g l[/math]

[math]\omega_1^2=\frac g l+\frac {2k} m[/math]

[math]z_1\;[/math] i [math]z_2\;[/math] opisują drgania normalne układu, natomiast [math]\omega_1[/math] i [math]\omega_2[/math] są częstościami własnymi. Po łatwych przekształceniach otrzymujemy rozwiązania na ruch obu wahadeł:

[math]x_1=\frac 1 2(A_1cos(\omega_1t+\phi_1)+A_2\cos(\omega_2t+\phi_2))[/math]

[math]x_2=\frac 1 2(A_1cos(\omega_1t+\phi_1)-A_2\cos(\omega_2t+\phi_2))[/math]

Widzimy więc, że ruch układu jest superpozycją dwóch drgań normalnych. Rozpatrywany przykład był dość prosty i metodą odejmowania i dodawania równań ruchu mogliśmy łatwo znaleźć dwa rozwiązania. W innych układach fizycznych nie zawsze taka prosta metoda pozwala znaleźć rozwiązania. Istnieje jednak pewna ogólna “recepta” postępowania w przypadku układu o wielu stopniach swobody. Załóżmy, że układ ruchu jest opisany następującym układem równań liniowych:

[math]m_1\frac{\mathrm d^2x_1}{\mathrm dt^2}+a_{11}x_1+a_{12}x_2+a_{13}x_3+\ldots=0[/math]

[math]m_2\frac{\mathrm d^2x_2}{\mathrm dt^2}+a_{21}x_1+a_{22}x_2+a_{23}x_3+\ldots=0[/math]

[math]m_3\frac{\mathrm d^2x_3}{\mathrm dt^2}+a_{31}x_1+a_{32}x_2+a_{33}x_3+\ldots=0[/math]

[math]\ldots\ldots\ldots[/math]

W pierwszym kroku szukamy drgań (modów) normalnych, a więc postulujemy rozwiązanie postaci: [math]x_i = A_i\cos(\omega t+\delta)[/math], a następnie przyrównujemy do zera wyznacznik otrzymanej macierzy [math]\mathrm{det}\left[ a'_{ij}\right][/math] dzięki czemu znajdujemy częstości własne a następnie postacie drgań normalnych.

Procedurę tę przećwiczmy na rozpatrywanym wyżej przykładzie dwóch sprzężonych wahadeł. Do układu równań:

[math]\frac{d^2x_1}{\mathrm dt^2}+\frac{g}{l}x_1-\frac k m(x_2-x_1)=0[/math]

[math]\frac{d^2x_2}{\mathrm dt^2}+\frac{g}{l}x_2+\frac k m(x_2-x_1)=0[/math]

podstawiamy postulowane rozwiązania:

[math]x_1=A\cos(\omega t+\delta)[/math]

[math]x_2=B\cos(\omega t +\delta)[/math]

Stąd otrzymujemy macierz:

[math]\left| \begin{array}{cc} \frac k m +\frac g l -\omega^2 & -\frac k m \\ -\frac k m & \frac k m +\frac g l -\omega^2 \end{array} \right|\left(\begin{array}{c}A\\B\\\end{array}\right) =0[/math]

Wyznacznik macierzy przyrównujemy do zera, co daje: [math]\left(\frac g l +\frac k m -\omega^2\right)-\left(\frac k m\right)^2=0[/math], a stąd znajdujemy dwie częstości własne (dla większej liczbie stopni swobody, wymiary macierzy są większe i otrzymujemy więcej częstości własnych): [math]\omega_1^2=\frac g l,\ \omega_2^2=\frac g l +\frac{2k}m[/math].

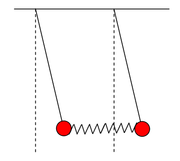
Mod 1 [math]\left(\omega_1=\sqrt{\frac g l}\right)[/math]

Postać drgań normalnych mod 1.

Dla tego modu normalnego oba wahadła drgają z częstością kołową taką jak dla wahadła swobodnego, a więc tak jakby nie było sprężyny. A więc odległość między wahadłami podczas ruchu jest taka sama (równa długości swobodnej sprężyny). Postać drgań pokazano na rysunku Figure 2.

Podstawiając częstość własną do macierzy znajdujemy, że:

[math]\left(\frac k m +\frac g l -\frac g l\right)A-\frac k m B =0 \Longrightarrow A=B[/math]

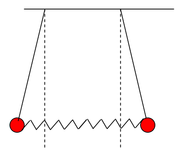
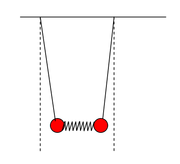
Mod 2 [math]\left(\omega_2^2=\frac g l +\frac{2k}m\right)[/math]

Podstawiając częstość własną do macierzy znajdujemy postać drgań:

[math]\left(\frac k m +\frac g l -\frac g l\right)A-\frac k m B =0\Longrightarrow B=-A[/math]

W tym przypadku amplitudy drgań obu wahadeł są takie same co do wartości ale różnią się znakiem, tzn. oba wahadła poruszają się w przeciwne strony, co ilustruje rysunek Figure 3 i Figure 4.

Mod 2 drgań wahadeł sprzężonych.

Mod 2 drgań wahadeł sprzężonych.

Ogólne rozwiązanie (czyli ogólny ruch układu dwóch sprzężonych wahadeł) jest kombinacją liniową obu modów normalnych, czyli:

[math]\left(\begin{array}{c}x_1\\x_2\end{array}\right) = A_1 \left(\begin{array}{c}1\\1\end{array}\right)\cos(\omega_1t+\delta_1)+A_2\left(\begin{array}{c}1\\-1\end{array}\right)\cos(\omega_2t+\delta_2)[/math]

Nasze rozważania dotyczące dwóch sprzężonych wahadeł rozszerzmy do siły wymuszającej działającej na wahadło pierwsze, tak jak na rysunku Figure 5.

Schemat układu dwóch sprzężonych wahadeł z siłą wymuszającą.

Przyjmijmy, że siła wymuszająca ma postać: [math]F_0\cos\Omega t[/math]. W tym przypadku równania ruchu mają postać:

[math]m\frac{\mathrm d x_1^2}{\mathrm d t^2} = -\frac{mg}l x_1 +k(x_2-x_1)+F_0\cos\Omega t[/math]

[math]m\frac{\mathrm d x_2^2}{\mathrm d t^2} = -\frac{mg}l x_2 -k(x_2-x_1)[/math]

Rozwiązania jednorodne znaleźliśmy wyżej. Rozwiązania szczególnego poszukujemy postaci: [math]x_i = A_i\cos\Omega t[/math]. Podstawiając postulowane rozwiązania do równań ruchu otrzymujemy układ równań liniowych, które rozwiązujemy z metodą wyznaczników:

[math]\left[\begin{array}{cc} \frac g l +\frac k m -\Omega^2 & -\frac k m\\-\frac k m & \frac g l +\frac k m -\Omega^2 \end{array}\right] \left[\begin{array}{c}A_1\\A_2\end{array}\right] = \left[\begin{array}{c}f_0\\0\end{array}\right][/math]

Wyliczamy wyznaczniki:

[math]W=\left( \frac g l +\frac k m -\Omega^2\right)^2-\left(\frac k m\right)^2 = (\omega_2^2-\Omega^2)(\omega_1^2-\Omega^2)[/math]

gdzie:

[math]\omega_1^2=\frac g l,\ \omega_2^2=\frac g l +\frac {2k} m[/math]

[math]W_1=\left|\begin{array}{cc}f_0&-\frac k m\\ 0 &\omega_1^2+\frac k m -\Omega^2\end{array}\right|=f_0\left(\omega_1^2+\frac k m -\Omega^2\right)[/math]

[math]W_2=\left|\begin{array}{cc}\omega_1^2+\frac k m -\Omega^2&f_0\\-\frac k m& 0 \end{array}\right|=f_0\frac k m [/math]

Następnie otrzymujemy wyrażenia na amplitudy:

[math]A_1=\frac {W_1}W=f_0\frac{\omega_1^2+\frac k m -\Omega^2}{(\omega_2^2-\Omega^2)(\omega_1^2-\Omega^2)}=\frac{f_0}{2}\left(\frac 1 {\omega_1^2-\Omega^2}+\frac 1 {\omega_2^2-\Omega^2}\right)[/math]

[math]A_2 = \frac{W_2}W=f_0\frac{\frac k m}{(\omega_2^2-\Omega^2)(\omega_1^2-\Omega^2)}=\frac{f_0}{2}\left(\frac 1 {\omega_1^2-\Omega^2}-\frac 1 {\omega_2^2-\Omega^2}\right)[/math]

A stąd rozwiązanie ruchu wahadeł:

[math]x_{1,2} =\frac{f_0}{2} \left(\frac 1 {\omega_1^2-\Omega^2}\pm\frac 1 {\omega_2^2-\Omega^2}\right)\cos\Omega t +\frac 1 2 (C_1\cos(\omega_1 t+\phi_1)\pm C_2\cos(\omega_2 t +\phi_2)) [/math]

Dwa ostatnie składniki są rozwiązaniami jednorodnymi. Zwykle jednak w każdym rzeczywistym układzie fizycznym występują siły oporu. W takim przypadku rozwiązanie jednorodne powinno zanikać z czasem i po dostatecznie długim czasie można je pominąć. Dla uproszczenia rozważań przyjmiemy, że w rozpatrywanym układzie siły oporu są bardzo małe, tzn. rozwiązanie szczególne przyjmujemy takie jakby nie było tłumienia, natomiast rozwiązanie jednorodne pomijamy, zakładając, ze zanikło do zera. Pozostaje wtedy rozwiązanie szczególne:

[math]x_{1,2} =\frac{f_0}{2} \left(\frac 1 {\omega_1^2-\Omega^2}\pm\frac 1 {\omega_2^2-\Omega^2}\right)\cos\Omega t[/math]

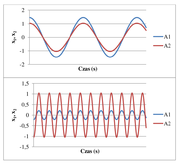
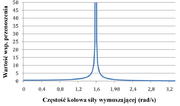
Zwróćmy uwagę, że dla [math]\Omega =\sqrt{\frac{\omega_1^2+\omega_2^2}{2}}[/math] amplituda [math]A_1=0[/math], natomiast amplituda [math]A_2[/math] dla żadnej częstości siły wymuszającej nie przyjmuje wartości zero. Na rysunku Figure 6 pokazano położenie obu wahadeł dla różnych wartości parametru [math]\Omega[/math].

Położenie wahadeł w funkcji czasu dla [math]\omega_1 = 3,\ \omega_2 = 7,\ \frac{f_0}2=10[/math] oraz [math]\Omega=1[/math] (górny rysunek) lub [math]\Omega=5[/math] (dolny rysunek).

Na rysunku Figure 7 pokazano zależność wartości obu amplitud od częstości kołowej siły wymuszającej. Widzimy, ze dla częstości siły wymuszającej odpowiadającej częstościom własnym układu amplitudy drgań wahadeł dążą do nieskończoności.

ależność amplitud drgań wahadeł od częstości siły wymuszającej. Przyjęto następujące częstości własne: [math]\omega_1=1,\ \omega_2=2[/math].

Dla układów, takich jak przez nas rozpatrywany wprowadza się współczynnik przenoszenia będący ilorazem amplitudy drgań drugiego wahadła do amplitudy drgań pierwszego wahadła, przy czym jako pierwsze wahadło rozumiemy to na które działa siła wymuszająca:

[math]\alpha = \frac{A_2}{A_1} = \frac{\omega_2^2-\omega_1^2}{\omega_2^2+\omega^2_1-2\Omega^2}[/math]

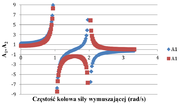
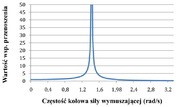
Na rysunku Figure 8 i Figure 9 pokazano wartość tego współczynnika i jego wartość bezwzględną.

Współczynnik przenoszenia. Obliczenia wykonano dla [math]\omega_1=1,\ \omega_2=2[/math].

Wartość bezwzględna współczynnika przenoszenia w funkcji częstości siły wymuszającej. Obliczenia wykonano dla [math]\omega_1=1,\ \omega_2=2[/math].

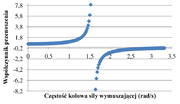
Widzimy, że dla częstości siły wymuszającej odpowiadającej częstościom własnym układu: [math]|\alpha|=1\rightarrow \Omega =\omega_1=\sqrt\frac g l\ \mathrm{lub}\ \Omega =\omega_2=\sqrt{\frac g l -\frac{2k}m}[/math], Natomiast Dla współczynnik przenoszenia wynosi: [math]\alpha = \frac{\omega_2^2}{\omega_2^2-2\Omega^2} = \frac{\frac k m}{\frac k m -\Omega^2}[/math]. Na rysunku Figure 10 pokazano tę zależność.

Współczynnik przenoszenia dla [math]\omega_1=0,\ \omega_2=2[/math]

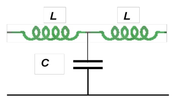
Przypadek ten nosi nazwę mechanicznego filtru dolnoprzepustowego i jest analogiem filtru elektrycznego pokazanego na rysunku Figure 11.

Elektryczny filtr dolnoprzepustowy.

W tym przypadku współczynnik przenoszenia wynosi:

[math]\alpha = \frac{U_{wyj}}{U_{wej}} = \frac{\omega_2^2}{\omega_2^2-2\Omega^2} = \frac{\frac{1}{LC}}{\frac{1}{LC}-\omega^2}[/math].

Na koniec naszych rozważań dotyczących drgań układów o wielu stopniach swobody zwróćmy uwagę, że dla układu o N stopniach swobody istnieje zawsze N postaci drgań normalnych o własnych charakterystycznych częstościach. Przechodząc z N do nieskończoności przechodzimy od układów dyskretnych do układów ciągłych. W zasadzie w układzie ciągłym powinniśmy mieć nieskończenie wiele postaci drgań normalnych. I tak jest w istocie; układ opisujemy w języku funkcji falowych:

[math]\overrightarrow{\Psi} = \hat e_x\Psi_x(x,y,z,t)+\hat e_y\Psi_y(x,y,z,t)+\hat e_z\Psi_z(x,y,z,t)[/math]

Funkcje te opisują wychylenie dowolnego punktu układu opisanego współrzędnymi [math](x, y, z)[/math] w funkcji czasu. Tym zagadnieniem będziemy się zajmować w następnym rozdziale.