Fizyka III/Fale elektromagnetyczne w kryształach dwójłomnych
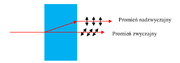
Istnieje pewien rodzaj kryształów, minerałów które wykazują zjawisko dwójłomności. Promień świetlny padający na taki materiał rozdziela się na dwa promienie tzw. promień zwyczajny i promień nadzwyczajny. Promień zwyczajny charakteryzuje się współczynnikiem załamania no różnym od współczynnika załamania dla promienia nadzwyczajnego (ne) oraz spełnia prawo załamania. Promień nadzwyczajny nie spełnia prawa załamania. Na rysunku Figure 1 pokazano przejście fali elektromagnetycznej przez kryształ dwójłomny. Poniżej zaś przedstawiono przykładowe kryształy dwójłomne wraz z wartościami współczynników załamania.
| Kryształ | [math]n_\mathrm o[/math] | [math]n_\mathrm e[/math] |
|---|---|---|
| Rutyl (TiO2) | 2,616 | 2,903 |
| Kwarc (SiO2) | 1,544 | 1,553 |
| Lód (H2O) | 1,309 | 1,310 |
| Saletra sodowa (NaNO3) | 1,585 | 1,337 |
| Szpat islandzki (CaCO3) | 1,658 | 1,486 |
| Korund (Al2O3) | 1,768 | 1,660 |
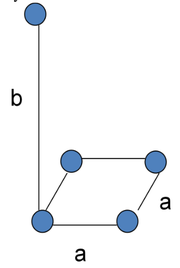
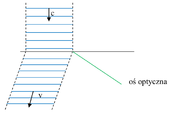
Jeśli współczynnik załamania [math]n_\mathrm e\gt n_\mathrm o[/math] to kryształ nazywamy optycznie dodatni, a jeśli [math]n_\mathrm o\gt n_\mathrm e[/math] to kryształ nazywamy optycznie ujemny. Wszystkie kryształy dwójłomne mają taka budowę mikroskopową, że istnieje wyróżniona oś, co schematycznie pokazano na rysunku Figure 2
W takich materiałach przenikalność elektryczna nie jest liczbą lecz tensorem. Dlatego zależność między natężeniem pola elektrycznego a indukcją wyraża się następująco:
- [math]\vec D=\hat\varepsilon\vec E[/math]
- [math]\hat\varepsilon =\left[\begin{array}{ccc}\varepsilon_\bot &0&0\\0& \varepsilon_\bot &0\\ 0 &0&\varepsilon_\| \end{array}\right][/math]
Promień zwyczajny ma polaryzację prostopadłą do płaszczyzny głównej utworzonej przez oś optyczną i promień padający, a jego prędkość wynosi:
- [math]v_\mathrm o = \frac c\sqrt{\varepsilon_\bot}=\frac c{n_\mathrm o}[/math].
Natomiast promień nadzwyczajny ma polaryzację prostopadłą do polaryzacji promienia zwyczajnego i rozchodzi się z prędkością:
- [math]v_\mathrm e = \frac c\sqrt{\varepsilon_\|}=\frac c{n_\mathrm e}[/math].
Czoło fali promienia zwyczajnego tworzy sferę, podczas gdy czoło fali promienia nadzwyczajnego tworzy elipsoidę obrotową o półosiach:
- [math]v_\mathrm e = \frac c\sqrt{\varepsilon_\|}=\frac c{n_\mathrm e},\ v_\mathrm o = \frac c\sqrt{\varepsilon_\bot}=\frac c{n_\mathrm o}[/math]
Zależność dyspersyjna dla promienia zwyczajnego jest bardzo prosta: [math]\omega = \frac c\sqrt{\varepsilon_\|}k[/math], natomiast dla promienia nadzwyczajnego:
- [math]\omega = c\sqrt{\frac{k_y^2}{\varepsilon_\|}+\frac{k_z^2}{\varepsilon_\bot}}[/math]
- [math]\frac{k_y^2}{\left(\frac{\sqrt{\varepsilon_\|}\omega}c\right)^2}+\frac{k_z^2}{\left(\frac{\sqrt{\varepsilon_\bot}\omega}c\right)^2}=1[/math]
W tym przypadku prędkość grupowa nie zawsze jest równoległa do wektora falowego.
Jeśli spolaryzowana liniowo fala pada na kryształ dwójłomny w ten sposób, że kierunek propagacji fali jest prostopadły do osi optycznej a wektor pola elektrycznego leży w płaszczyźnie tworzącej kąt 45° z osia optyczną to w zależności od grubości kryształu d i długości fali możemy uzyskać na wyjściu różne polaryzacje. Wektor pola elektryczne rozkładamy na składową równoległą i prostopadłą do osi optycznej. Obie składowe rozchodzą się z różnymi prędkościami.
Dlatego na wyjściu z kryształu pojawia się różnica faz między składowymi:
- [math]\Delta \phi =k(n_\mathrm o-n_\mathrm e)d = 2\pi\frac{d(n_\mathrm o-n_\mathrm e)}\lambda[/math].
Jeśli:
- [math]\Delta\phi =2m\pi [/math]
- [math]d (n_\mathrm o-n_\mathrm e)=(2m+1)\frac\lambda2[/math]
- [math]d=\frac{(m\lambda)}{2(n_\mathrm o-n_\mathrm e)}[/math],
to światło jest spolaryzowane liniowo, tak samo jak światło padające na płytkę.
Jeśli:
- [math]\Delta\phi =(2m+1)\pi[/math]
- [math]d(n_\mathrm o-n_\mathrm e)=(2m+1)\frac\lambda2[/math]
- [math]d=\frac{(2m+1)\lambda}{2(n_\mathrm o-n_\mathrm e)}[/math],
to światło jest spolaryzowane liniowo, ale kierunek pola [math]\vec E[/math] jest prostopadły do kierunku pola elektrycznego w świetle padającym.
Natomiast jeśli:
- [math]\Delta\phi =(2m+1)\frac\pi2[/math]
- [math]d(n_\mathrm o-n_\mathrm e)=(2m+1)\frac\lambda4[/math]
- [math]d=\frac{(2m+1)\lambda}{4(n_\mathrm o-n_\mathrm e)}[/math],
to światło jest spolaryzowane kołowo, koniec wektora pola elektrycznego zatacza okrąg. W tym przypadku kryształ dwójłomny nazywamy ćwierćfalówką.
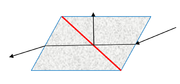
Kryształy dwójłomne są wykorzystywane do polaryzacji fali elektromagnetycznej (jako tzw. polaryzatory). Można je wykorzystywać „bezpośrednio”, np. kryształ turmalinu zielonego odpowiednio wycięty pochłania jeden z promieni lub budując pryzmaty. Przykład pryzmatu zbudowanego z dwóch kawałków szpatu islandzkiego sklejonych balsamem kanadyjskim pokazano na rysunku Figure 4.
Współczynniki załamania dla szpatu islandzkiego i balsamu kanadyjskiego wynoszą odpowiednio: [math]n_\mathrm o=1,658,\ n_\mathrm e=1,486,\ n_\mathrm{balsam kandayjski}=1,55[/math]. Kryształy są tak wycięte, że promień zwyczajny ulega całkowitemu wewnętrznemu odbiciu na granicy szpat islandzki – balsam kanadyjski, na wyjściu układu otrzymujemy spolaryzowany promień nadzwyczajny.
Jak wspominaliśmy wyżej zjawisko dwójłomności występuje w materiałach mających wyróżnioną oś. Dwójłomność można wymusić w materiałach nie wykazujących takich własności. Jedna z metod polega na ściskaniu lub rozciąganiu materiału (np. cienkiej foli celofanowej). Inna metoda polega na przyłożeniu dużego pola elektrycznego do niektórych substancji jak np. nitrobenzen. Cząsteczki nitrobenzenu mają kształt wydłużony. Ponadto posiadają moment dipolowy. Dla pojedyńczej cząsteczki indukowany przez falę elektromagnetyczną prąd zależy od kierunku (polaryzacji) pola elektrycznego. W ciekłym nitrobenzenie cząsteczki są ułożone chaotycznie. Zewnętrzne pole elektryczne powoduje uporządkowanie cząsteczek, a więc powstanie wyróżnionej osi. Efekt ten nosi nazwę zjawiska Kerra. Różnica współczynników załamania w tak wymuszonej dwójłomności jest proporcjonalna do kwadratu przyłożonego pola: [math]\Delta n =(n_\mathrm e-n_\mathrm o)=\kappa E^2\;[/math]. Przykładowe wartości współczynnika [math]\kappa[/math] dla wybranych cieczy są następujące:
| [math]\unit{\kappa}{\left[\frac{m^2}{V^2}\right]}[/math] | |
|---|---|
| Nitrobenzen | 2,44x10-12 |
| Nitrotoluen | 1,37x10-12 |
| Woda | 5,1x10-14 |