Fizyka III/Fale elektromagnetyczne w próżni
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
- [math]\mathrm{rot}\vec E = -\frac{\partial\vec B}{\partial t}[/math]
- [math]\mathrm{div}\vec B = 0[/math]
- [math]\mathrm{rot}\vec B =\mu_0\varepsilon_0 \frac{\partial\vec E}{\partial t}[/math]
- [math]\mathrm{div}\vec E = 0[/math],
gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a [math]\varepsilon_0[/math] i [math]\mu_0[/math] przenikalność elektryczną i magnetyczną.
Równanie pierwsze pokazuje, ze zmienne pole magnetyczne jest źródłem siły elektromotorycznej, natomiast równanie trzecie, że zmienne pole elektryczne jest źródłem pola magnetycznego. Dokonujemy następujących operacji matematycznych, liczymy:
- [math]\mathrm{rot}\ \mathrm{rot}\vec{E} =-\frac\partial{\partial t}\mathrm{rot}\vec B =- \frac\partial{\partial t} \mu_0\varepsilon_0 \frac{\partial \vec E}{\partial t}[/math].
Korzystając z tożsamości [math]\mathrm{rot}\ \mathrm{rot}\vec{E}=\nabla\mathrm{div}\vec E-\Delta\vec E[/math] oraz z faktu [math]\mathrm{div}\vec E=0[/math] otrzymujemy klasyczne równanie falowe na pole elektryczne:
- [math]\Delta\vec E = \frac 1{c^2}\frac{\partial^2\vec E}{\partial t^2}[/math].
Prędkość rozchodzenia się fali elektromagnetycznej c nazywamy prędkością światła. W próżni: [math]c=\frac 1\sqrt{\mu_0\varepsilon_0}=\unit{299792458}{\frac ms}[/math].
Zwróćmy uwagę, że pole elektryczne jest wielkością wektorową, a zatem każda ze składowych pola elektrycznego spełnia klasyczne równanie falowe. Analogiczne równania otrzymujemy na wektor indukcji pola magnetycznego. Mamy więc w sumie sześć równań na składowe pola elektrycznego i pola magnetycznego. Okazuje się, te sześć składowych obu pól nie są niezależne. Przyjmijmy, że rozwiązanie równania falowego jest w postaci harmonicznej biegnącej fali płaskiej: [math]\vec E =\vec E_0\cos(\vec k\vec r -\omega t)[/math]. Korzystając z równania: [math]\mathrm{div}\vec E = \frac{\partial E_x}{\partial x} +\frac{\partial E_y}{\partial y}+ \frac{\partial E_z}{\partial z}=0[/math], otrzymujemy: [math](E_{0x}k_x+E_{0y}k_y+E_{0z}k_z)(-\sin(\vec k\vec r-\omega t))=0[/math].
Równanie to jest spełnione dla każdej chwili czasu co oznacza, że: [math]\vec E\cdot\vec k=0[/math] czyli [math]\vec E\bot \vec k[/math]. Analogicznie dla wektora indukcji pola magnetycznego: [math]\vec B\cdot\vec k=0\Longrightarrow \vec B\bot \vec k[/math]. To oznacza, że fala elektromagnetyczna jest falą poprzeczną. Wektory pola elektrycznego i indukcji pola magnetycznego są prostopadłe do kierunku rozchodzenia się fali.
Okazuje się, że istnieje również związek łączący pole elektryczne i magnetyczne. Korzystając z równania Maxwella oraz przyjmując, że (daleko od źródła)
- [math]\vec E =\vec E_0\cos(\vec k\vec r -\omega t)\;[/math]
- [math]\vec B =\vec B_0\cos(\vec k\vec r -\omega t)\;[/math]
otrzymujemy następująca zależność:
- [math]\vec{B} = \frac 1\omega\left(\vec k\times\vec E\right)=\frac 1 c\left(\vec n\times\vec E\right)[/math]
- [math]\vec n=\frac{\vec k}k[/math]
czyli:
- [math]\vec B\bot \vec E[/math]
- [math]B=\frac Ec[/math].
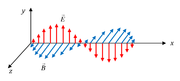
A zatem dla fali elektromagnetycznej w próżni wektory pola elektrycznego i indukcji pola magnetycznego są prostopadłe do siebie. Drgania wektorów obu pól odbywają się w fazie. Przykład biegnącej, harmonicznej fali elektromagnetycznej pokazano na rysunku Figure 1.
Fale elektromagnetyczne, jak każde fale przenoszą energię. Korzystając ze wzoru na gęstość energii pola elektromagnetycznego: [math]\rho_E=\frac{\varepsilon_0\vec E^2}2+\frac{\vec B^2}{2\mu_0}[/math], łatwo można otrzymać zasadę zachowania energii w następującej postaci: [math]\frac{\partial\rho_E}{\partial t}+\frac 1{\mu_0}\mathrm{div}\left(\vec E\times\vec B\right)=-\vec E\vec j[/math].
Widzimy, że suma zmiany energii elektromagnetycznej na jednostkę czasu w pewnej objętości i energii wypływającej w jednostce czasu przez powierzchnię ograniczającą tę objętość jest równa wziętej ze znakiem minus pracy wykonanej w jednostce czasu przez pola nad źródłami w tej objętości. Wielkość [math]\vec S=\frac 1{\mu_0}\left(\vec E\times\vec B\right)[/math] nazywamy wektorem Poyntinga. Wektor ten ma sens szybkości przepływu energii przez jednostkę powierzchni, a więc wartość średnia wektora Poyntinga jest natężeniem fali elektromagnetycznej: [math]I=\langle S\rangle[/math]. Dla fali harmonicznej natężenie wynosi:
- [math]I=\frac 1{mu_0}\langle EB\rangle=\frac 1{c\mu_0}\langle E^2\rangle = \frac 1{c\mu_0}\langle E^2_0\cos^2(\vec k\vec r -\omega t)\rangle = I= \frac 1{2c\mu_0} E_0^2[/math].
Dla punktowych źródeł emitujących fale izotropowo [math]I=\frac{P_\mathrm{zrodla}}{4\pi r^2}[/math]. Korzystając z wyprowadzonych wzorów policzmy jakie natężenie pola elektrycznego oraz indukcji pola magnetycznego zaobserwujemy na powierzchni Ziemi od satelity telekomunikacyjnego znajdującego się [math]r=\unit{100}{km}[/math] nad Ziemią i emitującego fale ze źródła o mocy [math]P_\mathrm{stacji} =\unit{50}{kW}[/math].
Natężenia promieniowania wynosi: [math]I=\frac{P_\mathrm{stacji}}{\frac 1 2 4\pi r^2}=\unit{7,96\times 10^{-7}}{\frac W{m^2}}[/math], stad otrzymujemy:
- [math]E_0=\sqrt{2\mu_0 c I}=\unit{2,45\cdot 10^{-2}}{\frac Vm}[/math]
- [math]B_0=\frac {E_0}c = \unit{8,17\cdot 10^{-11}}T[/math].
Wartość pola magnetycznego jest bardzo mała, dlatego w telekomunikacji wykorzystywana jest detekcja pola elektrycznego.
Fale elektromagnetyczne padając na obiekt wywierają ciśnienie. Wzór na ciśnienie promieniowania elektromagnetycznego [math]p_p[/math] (wzór wyprowadza się korzystając z faktu, że pęd „światła” jest równy energii podzielonej przez prędkość światła) jest następujący:
- Jeśli światło jest całkowicie pochłaniane [math]p_p=\frac I c[/math],
- Jeśli światło jest całkowicie odbijane: [math]p_p=\frac 2 c I[/math].
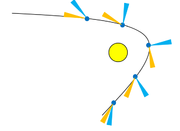
Ciśnienie promieniowania widoczne jest miedzy innymi w tworzeniu się dwóch warkoczy za kometa przechodzącą w pobliżu Słońca. Kiedy kometa przelatuje w pobliżu Słońca, z jej parującej lodowej powierzchni uwalniają się pył i naładowane cząstki. Wiatr słoneczny „ustawia” naładowane cząstki wzdłuż promienia od Słońca, natomiast drugi warkocz tworzy pył, który jest „odchylany” od orbity przez ciśnienie promieniowania (patrz rysunek Figure 2).
Podobnie jak dla fal dźwiękowych czy fal na strunie, również dla fal elektromagnetycznych z superpozycji dwóch fal biegnących w przeciwnych kierunkach otrzymujemy fale stojące, np.:
- [math]E_y(x,t)=E_0\left[\cos(kx+\omega t)-\cos(kx-\omega t)\right]=-2E_0\sin(kx)\sin(\omega t )[/math]
- [math]B_z(x,t)=B_0\left[-\cos(kx+\omega t)-\cos(kx-\omega t)\right]=-2B_0\cos(kx)\sin(\omega t )[/math]
Należy zwrócić uwagę, że dla fal stojących drgania wektora pola elektrycznego i wektora indukcji pola magnetycznego są przesunięte w fazie o 90°, podczas gdy dla fali biegnącej oba pola drgają z tą samą fazą. Elektromagnetyczne fale stojące o długości fali 12.2 cm wykorzystywane są w kuchenkach mikrofalowych.
Dla fal elektromagnetycznych musimy pamiętać, że pole elektryczne i magnetyczne są wielkościami wektorowymi. Jeśli drgania tych pól odbywają się w jednej płaszczyźnie to mówimy, że fala ma polaryzację liniową. Natomiast jeśli rzut wektora pola elektrycznego na płaszczyznę prostopadłą do kierunku rozchodzenia się fali zatacza okręgi, to mówimy o polaryzacji kołowej. W takim przypadku składowe pola opisane są następująco:
- [math]E_x=E_0\cos(kz-\omega t)[/math]
- [math]E_y=E_0\cos(kz-\omega t+\nicefrac \pi2)=E_0\sin(kz-\omega t)[/math]
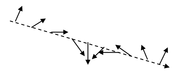
Na rysunku Figure 3 pokazano falę spolaryzowaną kołowo. Rzuty końca wektora pola elektrycznego i indukcji pola magnetycznego zataczają okręgi.
Dla fal elektromagnetycznych występuje podobnie jak dla fal mechanicznych efekt Dopplera, ale należy mocno podkreślić, że jest to efekt relatywistyczny, związany z transformacją z jednego układu odniesienia do drugiego. Dla efektu Dopplera fal elektromagnetycznych zgodnie z teorią względności nie ma znaczenia czy źródło, czy obserwator jest w ruchu, istotna jest tylko prędkość względna. Załóżmy, że w jednym układzie odniesienia falę opisujemy następująco: [math]E(z,t)=E_0\cos(2\pi f_0(t-\nicefrac zc))[/math].
W drugim układzie, poruszającym się względem pierwszego z prędkością v, falę tę opisujemy: [math]E(z,t)=E_0\cos(2\pi f(t-\nicefrac zc))[/math]. Korzystając z transformacji Lorentza otrzymujemy: [math]E(z,t)=E_0\cos\left(2\pi f_0\left(\frac{t+(\nicefrac v{c^2})z}{\sqrt{1-\nicefrac {v^2}{c^2}}}- \frac{z+vt}{\sqrt{1-\nicefrac {v^2}{c^2}}}\right)\right)=E_0\cos\left(2\pi f_0\frac{1-\nicefrac vc}{ \sqrt{1-\nicefrac {v^2}{c^2}}}(t-\nicefrac zc)\right)[/math].
Stąd częstotliwość fali w drugim układzie odniesienia wynosi: [math]f'=f_0\frac{1-\nicefrac vc}{\sqrt{1-\nicefrac {v^2}{c^2}}}[/math].
Wzór ten jest dla źródła lub obserwatora oddalających się od siebie; jeśli źródło lub obserwator zbliżają się do siebie we wzorze trzeba zmienić znak prędkości v. Dla małych prędkości v, wzór na zmianę częstotliwości można uprościć do postaci: [math]f=f_0(1-\nicefrac vc+\ldots)[/math], a stąd: [math]\frac c\lambda= \frac{c}{\lambda_0}(1-\nicefrac vc)[/math] i [math]v=\frac{\Delta \lambda}\lambda c[/math].
Znając zmianę częstotliwości lub długości fali można wyznaczyć względną prędkość układów odniesienia. Efekt ten jest wykorzystywany w radarach policyjnych do wyznaczanie prędkości pojazdów oraz w astronomii do wyznaczania prędkości gwiazd lub galaktyk. Efekt Dopplera uwzględniany jest również w nawigacji satelitarnej GPS.
Jeśli źródło (lub obserwator) porusza się pod kątem θ w kierunku obserwatora (źródła): to obserwowana częstotliwość wynosi: [math]f=f_0\frac{\sqrt{1-\nicefrac {v^2}{c^2}}}{1+v\cos\nicefrac\theta c}[/math].
Efekt zmiany częstotliwości ma więc miejsce nawet w przypadku gdy kąt [math]\theta =\frac \pi2[/math] (tzw. poprzeczny efekt Dopplera). Efekt taki nie występuje w przypadku fal mechanicznych rozchodzących się w ośrodkach sprężystych.