Fizyka III/Fale w ośrodkach o strukturze periodycznej

W dotychczasowych naszych rozważaniach ośrodek w którym rozchodzą się fale traktowaliśmy jako ośrodek ciągły, tzn. rozpatrywaliśmy przypadek gdy długość fali jest dużo większa niż nieciągłość ośrodka wynikająca z jego „ziarnistej” — atomowej budowy. Jeśli np. rozpatrujemy rozchodzenie się fal elastycznych o dużej częstotliwości w kryształach, to nieciągłości ośrodka nie można zaniedbać. Kryształy są zbudowane z atomów, które są rozmieszczone w przestrzeni w regularny, periodyczny sposób. Wiele własności drgań atomów w kryształach dobrze można opisać w sposób klasyczny traktując kryształ jako zbiór mas połączonych sprężynkami. Na początek poszukajmy związku dyspersyjnego dla jednowymiarowego nieskończonego łańcucha jednakowych mas m, odległych w stanie równowagi o a i połączonych jednakowymi sprężynkami o stałej sprężystości α (patrz rysunek Figure 1).

Schemat układu jednakowych mas.

Wychylenie n-tej masy z położenia równowagi oznaczamy [math]\Psi_n\;[/math]. Dla n-tej masy możemy napisać równanie ruchu uwzględniające siły harmoniczne działające na tę masę a pochodzące od mas sąsiednich:

[math]m\frac{\mathrm d^2\Psi_n}{\mathrm dt^2}=\alpha(\Psi_{n+1}-\Psi_n)-\alpha(\Psi_{n}-\Psi_{n-1})[/math].

Oczywiście analogiczne równania możemy wypisać dla każdej masy i otrzymamy nieskończony układ równań. Rozwiązań równań poszukujemy w postaci fal biegnących (w zapisie zespolonym): [math]\Psi_n(t)=Ae^{i(kna-\omega t)}[/math]. Po podstawieniu postulowanego rozwiązania do równania łatwo znajdujemy związek dyspersyjny:

[math]\omega =2\sqrt\frac \alpha m[/math].

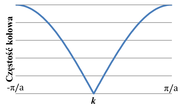
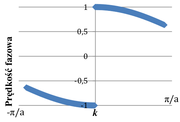
Otrzymaliśmy nieliniową zależność częstości kołowej od wartości wektora falowego (patrz rysunek II.6.2) oraz prędkość fazową zależną od długości fali:

[math]v_f =\frac\omega k=\frac 2 k\sqrt\frac \alpha m|\sin\frac{ka}2|[/math].

Zwróćmy uwagę, że dla małych wartości k, a więc dla dużych wartości długości fali, sinus możemy rozwinąć w szereg i wówczas otrzymamy liniowy związek dyspersyjny, tak jak dla fal dźwiękowych. Prędkość rozchodzenia się fali o dużych długościach (a więc gdy [math]\lambda \gg a[/math]) jest wówczas taka sama jak dla struny:

[math]v_f\rightarrow_{k\rightarrow 0}\sqrt\frac\alpha m a=\sqrt\frac{\alpha a}{\nicefrac m a}=\sqrt\frac{F_0}{\rho S}[/math].

Ze względu na to, ze rozpatrywany nieskończony układ mas jest periodyczny, wartości wektora falowego ograniczyliśmy do wartości [math]k_\max=\pm\frac\pi a[/math]. Wartości tej odpowiada najmniejsza możliwa długość fali biegnącej w układzie: [math]\lambda_\min=\frac{2\pi}{k_\max}=2a[/math]. Ta najmniejsza wartość jest zrozumiała, bo odpowiada sytuacji drgań, że najbliżsi sąsiedzi zbliżają się i oddalają od siebie.

Zależność dyspersyjna dla nieskończonego łańcucha identycznych mas.

Prędkość fazowa dla fali rozchodzącej się w nieskończonym łańcuchu mas.

W fizyce ciała stałego drgania elastyczne atomów sieci nazywane są fononami. Rodzaj drgań otrzymanych dla rozpatrywanego przypadku nazywany jest fononami akustycznymi.

Układ dwóch rodzajów mas.

Przejdźmy teraz do układu pokazanego na rysunku Figure 4, tj. układu dwóch rodzajów mas: m i M połączonych takimi samymi sprężynkami o stałej sprężystości α. W tym przypadku otrzymujemy układ równań:

[math]M\frac{\mathrm d^2\Psi_{2n}}{\mathrm dt^2}=\alpha(\Psi_{2n+1}\Psi_{2n-1}-2\Psi_{2n})[/math],

[math]m\frac{\mathrm d^2\Psi_{2n+1}}{\mathrm dt^2}=\alpha(\Psi_{2n+2}\Psi_{2n}-2\Psi_{2n+1})[/math].

Ponieważ mamy dwa rodzaje mas, to postulujemy następujące rozwiązania w postaci fal biegnących:

[math]\Psi_{2n}=Ae^{i(2nka-\omega t)}[/math],

[math]\Psi_{2n+1}=Be^{i((2n+1)ka-\omega t)}[/math].

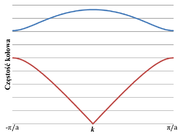
Po podstawieniu do równań łatwo otrzymujemy dwa rozwiązania (patrz rysunek: Figure 5)

[math]\omega_\pm^2=\alpha\left(\frac 1m \frac 1M\right)\pm\alpha\sqrt{\left(\frac 1m \frac 1M\right)^2-\frac4{mM}\sin^2ka}[/math]

Zależność dyspersyjna dla nieskończonego łańcucha dwóch rodzajów mas.

Fakt, że układ składa się z dwóch rodzajów mas spowodował, ze otrzymaliśmy dwie gałęzie zależności częstości od wartości wektora falowego. Dolna gałąź odpowiada drganiom, które w fizyce ciała stałego są nazywane fononami akustycznymi a górna gałąź fononami optycznymi. Dla „prawdziwego” kryształu tj. kryształu w trzech wymiarach oprócz rozważanych drgań podłużnych należy uwzględnić również drgania poprzeczne, które są nazywane fononami poprzecznymi. W przypadku kryształów zbudowanych z co najmniej dwóch różnych rodzajów atomów (tzw. baza jest co najmniej dwu atomowa) podczas drgań poprzecznych (fonony poprzeczne) opisanych górną gałęzią indukowany jest moment dipolowy, dzięki czemu ten rodzaj drgań może oddziaływać z falą elektromagnetyczną. Dlatego gałąź ta jest nazywana fononami optycznymi.