Fizyka III/Interferencja
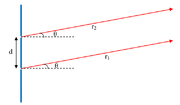
Zjawisko interferencji jest jednym z najbardziej charakterystycznych zjawisk dla fal. Występuje dla wszystkich rodzajów fal. Mimo że ta część dotyczy fal elektromagnetycznych, to będziemy się odnosić do wszystkich rodzajów fal. Dlatego zastosujemy opis skalarny, tzn. będziemy używać opisu funkcji falowej [math]\Psi[/math], która może opisywać fale w strunie, fale dźwiękowe lub fale elektromagnetyczne. Zjawisko interferencji czyli nakładania się (superpozycji) fal występuje tylko w przypadku gdy interferujące fale są spójne. Interferencja fal emitowanych przez dwa spójne źródła została pokazana w doświadczeniu Younga. Schemat doświadczenia pokazano na rysunku Figure 1.
Wiązka światła pochodząca z jednego źródła po przejściu przez jedną wąską szczelinę pada na dwie następne wąskie szczeliny odległe od siebie o d. Szczeliny te traktujemy jako dwa punktowe źródła spójnych fal kulistych. Na ekranie znajdującym się w dużej odległości od szczelin notowane są ciemne i jasne prążki. Fale pochodzące od obu szczelin opisujemy następującymi funkcjami falowymi:
- [math]\Psi_1(r_1,t)A(r_1)\cos(kr_1-\omega t)\;[/math]
- [math]\Psi_2(r_2,t)A(r_2)\cos(kr_2-\omega t)\;[/math]
gdzie zgodnie z wcześniej przeprowadzoną dyskusją [math]A(r)=\frac{A_0}r\;[/math] dla fali rozchodzącej się w 3 wymiarach lub [math]\frac{A_0}\sqrt{r}\;[/math], jeśli fala rozchodzi się w 2 wymiarach. Dla dużych odległości możemy przyjąć:
- [math]A(r_1)\approx A(r_2)\cong A\left(\frac{r_1+r_2}2\right)=A(r_\mathrm{sr})[/math]
Względny błąd wynikający z tego przybliżenia dla wynosi 10% dla przypadku trójwymiarowego i 5% dla przypadku dwuwymiarowego. Na ekranie obserwujemy wynik zsumowania obu fal:
- [math]\Psi_1(r_z,t)+\Psi_2(r_2,t)=2A(r_\mathrm{sr})\cos\left(k\frac{r_1-r_2}2\right)\cos(kr_\mathrm{sr}-\omega t)[/math].
Pierwszy czynnik (cosinus) opisuje przestrzenną modulację, natomiast drugi wraz z amplitudą falę kulistą. Na ekranie otrzymujemy maksima interferencyjne (jasne prążki) gdy spełniony jest warunek:
- [math]\cos\left(k\frac{r_1-r_2}2\right)=\pm 1[/math],
- [math]k\frac{r_1-r_2}2=m\pi[/math],
czyli gdy różnica dróg optycznych obu promieni jest równa wielokrotności długości fali: [math]r_1-r_2=m\lambda[/math] (m jest liczbą całkowitą).
Wygaszenie fal (ciemne prążki) występują natomiast gdy:
- [math]\cos\left(k\frac{r_1-r_2}2\right)=0[/math]
- [math]k\frac{r_1-r_2}2=\frac{2m+1}2\pi[/math].
A więc dla różnicy dróg optycznych obu promieni równej nieparzystej wielokrotności połowy długości fali: [math]r_1-r_2=\frac{2m+1}2\lambda[/math].
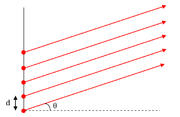
Często przy opisie interferencji, gdy ekran znajduje się w bardzo dużej odległości od szczelin (w porównaniu z odległością między szczelinami) stosujemy przybliżenie Fraunhofera. Przybliżenie to polega na tym, że przyjmujemy, że oba promienie są równoległe do siebie, tak jak to pokazano na rysunku Figure 2. W takim przypadku:[math]r_1-r_2=d\sin\theta[/math], a warunek na maksima interferencyjne jest następujący: [math]d\sin\theta =m\lambda[/math], a na minima: [math]d\sin\theta =\frac{2m+1}2\lambda[/math].
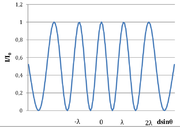
Kąt [math]\theta\;[/math] oznacza kąt jaki tworzą promienie do osi układu. Natężenie światła obserwowane na ekranie w przybliżeniu Fraunhofera ma postać (patrz rysunek Figure 3): [math]I=I_0\cos^2\left(\frac 12 kd\sin\theta\right)=I_0\cos^2\left(\frac{\pi d}\lambda \sin\theta\right)[/math].
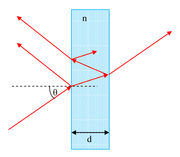
Zjawisko interferencji bardzo „ładnie” widać na cienkich warstwach lub błonach, np. na bańkach mydlanych lub na płytkiej kałuży rozlanej benzyny. Interferencja zachodzi między falami, które ulegają wielokrotnemu odbiciu od granicy ośrodków, co ilustruje rysunek Figure 4. Załóżmy, że cienka płytka jest ośrodkiem o współczynniku załamania n, natomiast współczynnik załamania powietrza przyjmijmy 1.
Interferencję obserwujemy zarówno w świetle odbitym jak i przechodzącym. Dla wiązki odbitej różnica faz między fala odbitą na pierwszej powierzchni granicznej i falą odbitą na drugiej powierzchni wynosi:
- [math]\Delta \phi_\mathrm o =k2dn\cos\theta-\pi[/math].
Pierwszy składnik pochodzi z różnicy dróg optycznych, natomiast zmiana fazy o [math]\pi\;[/math] jest związana z odbiciem fali od ośrodka optycznie gęstszego (wzory Fresnela). Dla fali przechodzącej różnica faz wynosi:[math]\Delta \phi_\mathrm o =k2dn\cos\theta[/math] . Dla “matematycznego” uproszczenia problemu załóżmy, że kąt padania jest bardzo mały ([math]\theta\approx 0[/math]), wówczas dla fali odbitej i fali przechodzącej różnica faz wynosi odpowiednio: [math]\Delta\phi_\mathrm o = 2kdn-\pi\Delta\pi_\mathrm p=k2dn[/math]. W takim przypadku dla fali odbitej zachodzi (m — liczba całkowita):
- Interferencja konstruktywna gdy: [math]2d=(2m+1)\frac\lambda{2n}[/math].
- Interferencja destruktywana gdy: [math]2d=m\frac\lambda n[/math].
Dla fali przechodzącej otrzymujemy:
- Interferencję konstruktywną gdy: [math]2d=m\frac\lambda n[/math].
- Interferencję destruktywną gdy: [math]2d=(2m+1)\frac\lambda{2n}[/math].
Jeśli będziemy obserwować interferencję na cienkich warstwach w świetle białym to zobaczymy kolorowe prążki, przy czym w świetle przechodzącym będziemy obserwować barwy uzupełniające do barw widzianych w świetle odbitym. Poniżej zebrano obserwowane barwy dla różnych grubości warstw.
| Grubość warstwy (nm) | światło odbite | światło przechodzące |
|---|---|---|
| 0 | czarna | biała |
| 97 | szara | żółtawobiała |
| 218 | jasnoszara | żółtobrunatna |
| 257 | żółtawobiała | karminowa |
| 281 | słomkowożółta | ciemnofiołkowa |
| 382 | jaskrawożółta | niebieska |
| 430 | żółtobrunatna | szaroniebieska |
| 558 | czerwona | bladozielona |
| 565 | purpurowa | jasnozielona |
| 580 | indygo | złotożółta |
| 664 | lazurowa | pomarańczowa |
| 747 | zielona | jasnokarminowa |
| 826 | jasnozielona | purpurowa |
| 843 | żółtawozielona | fioletowopurpurowa |
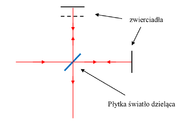
Ze zjawiskiem interferencji wiąże się bardzo ważny eksperyment, tzw. doświadczenie Michelsona-Morleya. Doświadczenie to miało pokazać istnienie „eteru” — ośrodka w którym poruszają się fale elektromagnetyczne. Wynik eksperymentu okazał się negatywny. Ale jest to jeden z nielicznych przypadków, że negatywny wynik przyczynił się istotnie do rozwoju fizyki. Doświadczenie wykonano za pomocą interferometru noszącego obecnie nazwę interferometru Michelsona. Przyrząd ten stał się jednym z najważniejszych narzędzi badawczych w fizyce doświadczalnej. Schemat interferometru pokazany jest na rysunku Figure 5. Interferometr składa się z płytki światło dzielącej i dwóch zwierciadeł umieszczonych w dwóch ramionach interferometru tworzących kąt prosty. Płytka część światła odbija pod katem 45°, a część przepuszcza wzdłuż kierunku biegu promienia pierwotnego. Oba rozdzielone promienie odbijają się od zwierciadeł i wracają do płytki, która tym razem łączy oba promienie. Detektor rejestruje sygnał pochodzący od obu interferujących fal. Jedno z luster jest ruchome. Ruch zwierciadła wprowadza różnicę faz między dwiema wiązkami. Pomiar polega zatem na zarejestrowaniu sygnału w funkcji położenia ruchomego lustra, czyli na otrzymaniu tzw. interferogramu. Za pomocą transformaty Fouriera sygnał jest przeliczany na widmo natężenia światła w funkcji długości fali. Położenie ruchomego lustra jest wyznaczane z niezwykła precyzją za pomocą pomiaru interferencji monochromatycznej wiązki światła laserowego o znanej długości. Dzięki temu za pomocą interferometru Michelsona uzyskuje się znakomitą zdolność rozdzielczą mierzonych widm optycznych. Wracając do doświadczenia Michelsona –Morleya, jeśli interferometr porusza się (wraz z Ziemią) w ośrodku zwanym „eterem”, to drogi jakie muszą pokonać oba promienie nie się równoważne. Jeśli interferometr obrócimy o 90° to prążki interferencyjne powinny się przesunąć o [math]\Delta N =\frac{2d}\lambda\left(\frac uc\right)^2[/math] gdzie d jest długością ramienia interferometru, a u prędkością interferometru (Ziemi) względem „eteru” [math]\left(\nicefrac uc=10^{-4}\right)[/math]. W oryginalnym doświadczeniu d = 11 m, [math]\lambda=\unit{5,9\cdot10^{-7}} m[/math], co daje spodziewane przesunięcie [math]\Delta N=0,4\pm0,01\;[/math]. Jak wspominaliśmy wyżej, wynik eksperymentu był negatywny.
Na rysunku Figure 6 pokazano inny rodzaj interferometru zwany interferometrem Fabry-Perota. W tym przypadku interferują fale ulegające wielokrotnemu odbiciu od dwóch „ścianek” (luster) — cienkich warstw.
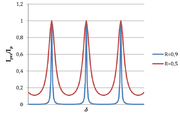
Przesunięcie fazowe między „sąsiednimi” falami przechodzącymi wynosi: [math]\delta =2\pi\frac{2d\cos\theta}\lambda[/math]. Natężenie światła przechodzącego wyraża się wzorem:
- [math]I_\mathrm{prz}=I_\mathrm p\frac 1{1+\frac{4R\sin^2\nicefrac\delta 2}{(1-R)^2}}[/math],
gdzie [math]I_\mathrm p\;[/math] jest natężeniem fali padającej, a R współczynnikiem odbicia luster. Rysunek III.5.7. pokazuje natężenie fali przechodzącej w funkcji [math]\delta\;[/math] dla różnych wartości R. Im R bliższe wartości 1, tym linie interferencyjne są węższe.
Na koniec naszych rozważań poszukajmy obrazu interferencyjnego pochodzącego od N identycznych punktowych źródeł światła spójnego, tak jak pokazano na rysunku Figure 8.
Rachunek wykonamy w zapisie liczb zespolonych (bo tak jest wygodniej i łatwiej) w przybliżeniu Fraunhofera. Każde ze źródeł jest źródłem fali:
- [math]E_1=A^{i(kr-\omega t)}[/math]
- [math]E_2=A^{i(kr-\omega t-ka\sin\theta)}[/math]
- [math]\ldots[/math]
- [math]E_m=A^{i(kr-\omega t-(m-1)ka\sin\theta)}[/math]
- [math]ldots[/math]
- [math]E_N=A^{i(kr-\omega t-(N-1)ka\sin\theta)}[/math]
Suma wszystkich fal wynosi: [math]E=\Sigma_{m=1}^N E_m=Ae^{i(kr-\omega t)}\frac{1-e^{-iNka\sin\theta}}{1-e^{-ika\sin\theta}}[/math]. stąd natężenie światła obserwowane na ekranie wyraża się wzorem:
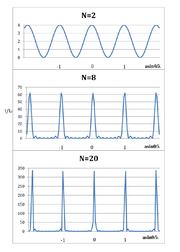
- [math]I=I_0\frac{\sin^2\left(\frac{Nka\sin\theta}2\right)}{\sin^2\left(\frac{ka\sin\theta}2\right)}[/math].
Tę zależność pokazano na rysunku Figure 9 dla różnej wartości N. W otrzymanym widmie występują maksima główne dla katów spełniających warunek: [math]ks\sin\theta =2\pi m[/math] (m jest liczbą całkowitą) oraz [math](N-2)[/math] maksimów wtórnych o znacznie mniejszym natężeniu.