Fizyka III/Matematyczny opis fali

W jaki sposób możemy matematycznie opisać falę?

Jak wspominaliśmy na koniec poprzedniego rozdziału układy ciągłe powinniśmy opisywać za pomocą funkcji falowej. Na początek ograniczmy nasze rozważania do układu jednowymiarowego, czyli fali rozchodzącej się strunie elastycznej. Spoczywająca struna rozciąga się wzdłuż osi OZ. W takim przypadku funkcja falowa ma postać:

[math]\overrightarrow{\Psi}(z,t) = \hat e_x\Psi_x(z,t)\Longrightarrow \Psi(z,t)[/math]

Funkcja ta opisuje wychylenie struny z położenia równowagi w punkcie z w chwili czasu t. Załóżmy, że koniec struny jest wprawiany w ruch harmoniczny: [math]\Psi(z=0,t)=A\cos\omega t[/math]. Zaburzenie to rozchodzi się w strunie z pewną prędkością [math]v[/math] i do punktu z dojdzie po czasie [math]t' = \nicefrac z v[/math] . Jeśli powiniemy siły oporu to wychylenie struny z położenia równowagi w punkcie z będzie takie samo jak końca struny ale przesunięte w czasie o [math]t'[/math], a zatem:

[math]\Psi(z,t)=A\cos\left[\omega\left( t-\frac z v\right)\right][/math]

Wyrażenie to opisuje falę harmoniczną biegnącą w prawo (zgodnie ze zwrotem osi OZ) w strunie. Często stosowane są inne zapisy:

[math]\Psi(z,t)=A\cos\left(\frac{\omega z}v-\omega t\right) =A\cos\left(\frac{2\pi f}vz-\omega t\right)=A\cos\left(\frac{2\pi}\lambda z -\omega t \right) =A\cos(kz-\omega t)[/math]

We wzorze występują następujące wielkości opisujące ruch falowy:

• [math]\lambda[/math] — odległość między punktami ośrodka o tej samej fazie — długość fali,
• [math]T[/math] — czas po którym wybrany punkt ośrodka będzie w tej samej fazie — okres drgań,
• [math]v[/math] — prędkość przemieszczania się zaburzeń o tej samej fazie — prędkość fazowa,
• [math]k[/math] — liczba falowa.

Następujące relacje zachodzą miedzy tymi wielkościami: [math]v=\frac \lambda T[/math], [math]\omega = 2\pi f =\frac{2\pi}T[/math], [math]k = \frac{2\pi}\lambda[/math].

Powyżej podaliśmy wzór opisujący falę harmoniczną rozchodzącą się w strunie wzdłuż osi OZ w prawo. Oczywiście analogiczna fala może się rozchodzić w przeciwnym kierunku, tj. w lewo, którą opisujemy:

[math]\Psi_-(z,t)=A\cos(kz+\omega t ) =A\cos\left[k(z+v t)\right][/math]

Fale harmoniczne powstają jeśli koniec struny wprawiany jest w ruch harmoniczny, ale zaburzenie końca może być dowolne. W związku z tym ogólna postać funkcji falowej ma postać:

[math]\Psi_-(z,t)=\Psi_1(z-vt)+\Psi_2(z+vt)\;[/math]

Możemy oczekiwać, że prędkość rozchodzenia się fali zależy od własności fizycznych ośrodka. Spróbujmy zbadać ten problem.

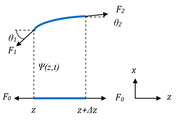
Załóżmy, że struna jest naciągnięta siłą [math]F_0[/math]. Wydzielmy kawałek struny o bardzo małej długości [math]\Delta z[/math] (patrz rysunek Figure 1).

Siły działające na element struny.

Wychylenie struny z położenia równowagi opisane jest funkcją falową: [math]\Psi(z,t)[/math]. Wypadkowa siła działająca na element odkształconej struny wynosi:

[math]F_x(t) = F_2\sin\theta_2-F_z\sin\theta_1[/math]

Uwzględniając siłę naciągu nici: [math]F_{1,2}\cos\theta_{1,2}\approx F_0[/math] oraz [math]\tg\theta = \frac{\partial \Psi}{\partial z}[/math] otrzymujemy:

[math]F_x(t) = F_0\left(\frac{\partial \Psi}{\partial z}\right) |_{z+\Delta z}-F_0\left(\frac{\partial \Psi}{\partial z}\right)|_{z} [/math][math]= F_0\frac{\left(\frac{\partial \Psi}{\partial z}\right)|_{z+\Delta z}-\left(\frac{\partial \Psi}{\partial z}\right) |_{z}}{\Delta z} \Delta z[/math]

Zbiegając z [math]\Delta z[/math] do zera ostateczna postać wypadkowej siły działającej na element struny wynosi:

[math]F_x(t) = F_0\Delta z \frac{\partial^2\Psi(z,t)}{\partial z^2}[/math]

Masa elementu struny wynosi z kolei: [math]\rho_0s\Delta z[/math], gdzie [math]\rho_0[/math] jest gęstością, a [math]s[/math] przekrojem poprzecznym struny. Ponadto pamiętając, że [math]\Psi(z,t)[/math] jest wychyleniem struny w punkcie [math]z[/math] z położenia równowagi, [math]\frac{\partial \Psi(z,t)}{\partial t}[/math] jest prędkością (poprzeczną) struny w punkcie [math]z[/math], [math]\frac{\partial^2 \Psi(z,t)}{\partial t^2}[/math] a [math]\frac{\partial^2 \Psi(z,t)}{\partial t^2}[/math] jej przyśpieszeniem w tym punkcie, otrzymujemy równanie:

[math]\rho_0s\Delta z \frac{\partial^2 \Psi(z,t)}{\partial t^2}=F_0\Delta z \frac{\partial^2 \Psi(z,t)}{\partial z^2}[/math]

A stąd po przekształceniach:

[math] \frac{\partial^2 \Psi(z,t)}{\partial t^2}=\frac{F_0}{\rho_0s}\frac{\partial^2 \Psi(z,t)}{\partial z^2}[/math].

Jest to tzw. klasyczne równanie falowe.

Sprawdźmy, czy postulowana wyżej ogólna postać funkcji falowe spełnia to równanie?

[math]\Psi(\xi)=\Psi(z-vt)\;[/math]

[math]\frac{\partial \Psi}{\partial t} =\frac{\partial \Psi}{\partial \xi} \frac{\partial \xi}{\partial t} =-v\frac{\partial \Psi}{\partial \xi} [/math]

[math]\frac{\partial^2 \Psi}{\partial t^2} =-v\frac{\partial^2 \Psi}{\partial \xi^2} \frac{\partial \xi}{\partial t} =v^2\frac{\partial^2 \Psi}{\partial \xi^2}[/math]

oraz

[math]\frac{\partial \Psi}{\partial z}=\frac{\partial \Psi}{\partial \xi} \frac{\partial \xi}{\partial z}=\frac{\partial \Psi}{\partial \xi}[/math]

[math]\frac{\partial^2 \Psi}{\partial z^2}=\frac{\partial^2 \Psi}{\partial^2 \xi} \frac{\partial \xi}{\partial z}=\frac{\partial^2 \Psi}{\partial \xi^2}[/math]

Stąd wynika, że postulowana postać funkcji falowej spełnia klasyczne równanie falowe pod warunkiem, że poszukiwana prędkość rozchodzenia sie fali wynosi:

[math]v=\sqrt{\frac{F_0}{\rho_0 s}}=\sqrt{\frac{F_0L}m}[/math]

Widzimy, że prędkość rozchodzenia się fali zależy od siły naciągu struny, jej przekroju i gęstości. Możemy też powiedzieć, że kwadrat tej prędkość jest proporcjonalny do siły przywracającej strunę (ośrodek) do równowagi, a odwrotnie proporcjonalny do „inercji” ośrodka „opierającej” się powrotowi ośrodka do równowagi.

Na początku tego rozdziału mówiliśmy, że z falą wiąże się transport energii. Policzmy transport mocy przez falę biegnącą w strunie. Moc ta wynosi:

[math]P(z,t)=F_{\bot}v_\bot = -F_0\tg\theta \frac{\partial \Psi}{\partial t} = -F_0 \frac{\partial \Psi}{\partial z}\frac{\partial \Psi}{\partial t}[/math]

Dla fali harmonicznej: [math]\Psi(z,t)=A\cos(kz-\omega t)\;[/math] otrzymujemy:

[math]P(z,t)=\rho_0 v s \omega^2 A^2\sin^2(kz-\omega t) = Zs\omega^2A^2\sin^2(kz-\omega t)\;[/math],

gdzie: wielkość [math]Z=\rho_0v\;[/math] nosi nazwę oporu falowego ośrodka (impedancji).

Wyrażenie na moc średnią jest następujące:

[math]\langle P(z,t)\rangle = \frac 1 2 Z\omega^2A^2[/math]

Używane jest też pojęcie natężenia fali [math]I=\frac{P_{\mathrm{sr}}}{s}[/math]. Dla struny natężenie to wynosi zatem: [math]I=\frac 1 2 Z\omega^2A^2[/math].

Rozpatrywana wyżej postać fali harmonicznej nosi nazwę fali biegnącej, fala rozchodzi sie w określonym kierunku. Na strunie może się rozchodzić wiele różnych fal. Wychylenie struny z położenia równowagi będzie efektem superpozycji wszystkich fal. Jeśli w strunie będą rozchodzić się dwie fale o tej samej częstości i o takich samych amplitudach, ale w przeciwnych kierunkach to w wyniku superpozycji otrzymamy:

[math]\Psi(z,t)=C(\cos(kz-\omega t)+\cos(kz+\omega t +\delta))=A\cos(kz+\alpha)\cos(\omega t +\phi)\;[/math].

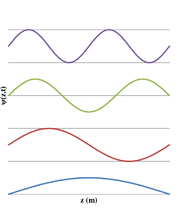
Otrzymaliśmy postać fali, która nosi nazwę fali stojącej. Część zależna od położenia jest rozseparowana od części zależnej od czasu. Możemy więc zapisać drgania struny następująco: [math]\Psi(z,t)=A(z)\cos(\omega t +\phi)[/math]. Dla pewnych punktów struny amplituda drgań wynosi zero. Takie punkty nazywamy węzłami fali stojącej. Natomiast punkty, których amplituda drgań jest największa nazywamy strzałkami. Fale stojące powstają np. na skończonej strunie. Jeśli końce struny są sztywno zamocowane w punkcie [math]z=0\ \mathrm{i}\ z=L[/math], to w tych punktach wychylenie struny z położenia równowagi wynosi oczywiście zero. Korzystając z tych warunków możemy łatwo znaleźć postacie fal stojących w strunie o długości [math]L[/math]. Postacie fal o czterech najniższych częstościach pokazano na rysunku Figure 2.

Przykład fal stojących na strunie o zamocowanych obu końcach.

Funkcja falowa ma postać:

[math]\Psi(z,t)=A\sin\left(2\pi\frac z{\lambda_n}\right)\cos(\omega t+\phi)[/math],

gdzie: [math]\lambda_n=\frac{2L}n[/math], [math]\omega^2=(2\pi f)^2[/math], [math]n=1, 2, 3, \ldots[/math]. Funkcje falową możemy też zapisać następująco:

[math]\Psi(z,t)=A\sin\left(\pi n \frac z L\right)\cos\left(\frac{n\pi}L\sqrt{\frac{T_0}{\rho_0s}}t+\phi\right)[/math].