Fizyka III/Ośrodki dyspersyjne
Dla fal rozchodzących się w strunie lub fal dźwiękowych rozchodzących się w ośrodkach ciągłych funkcja falowa spełnia klasyczne równanie falowe. W tych przypadkach, a więc dla ośrodków w których spełnione jest klasyczne równanie falowe, prędkość rozchodzenia się fali jest stała, nie zależy od częstotliwości (długości fali) [math]v=\frac\omega k=\mathrm{const}[/math]. Takie ośrodki nazywamy ośrodkami bezdyspersyjnymi.
Z kolei dla fal na wodzie czy fal elastycznych w kryształach związki dyspersyjne nie są liniowe:
- Fale w ośrodkach o strukturze periodycznej; [math]\omega=2\sqrt{\frac\alpha m}|\sin\frac{ka}2|[/math].
- Fale na wodzie; [math]\omega^2=\left(gk+\frac{\sigma k^2}{h\rho}\right)\mathrm{tgh}(kh)[/math].
Przykładów nieliniowych związków dyspersyjnych jest więcej. W tych przypadkach prędkość fazowa fali zdefiniowana jako [math]v_s=\frac \omega k[/math] nie jest stała i zależy od częstotliwości fali (długości fali). Ośrodek w którym prędkość fazowa zależy od długości fali nazywamy ośrodkiem dyspersyjnym.
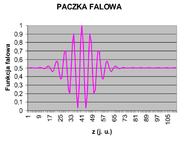
Do tej pory zajmowaliśmy się falami harmonicznymi, ale jak wspominaliśmy na początku rozważań o falach, fale mogą się rozchodzić również w postaci impulsów (paczek falowych), jak np. pokazany na rysunku Figure 1.
Matematycznie impuls możemy przedstawić jako złożenie fal harmonicznych o ciągłym widmie, czyli w postaci:
- [math]\Psi(z,t)=\int_{-\infty}^{+\infty} c(k)e^{i(kz-\omega(k)t)}\mathrm dk[/math],
gdzie widmo [math]c(k)[/math] możemy wyznaczyć ze znajomości kształtu impulsu w chwili początkowej: [math]c(k)=\frac 1{2\pi}\int_{-\infty}^{+\infty}\Psi(z,0)e^{-kz}\mathrm dz[/math].
Paczka falowa jest superpozycją wielu fal harmonicznych z zakresu tym większego, im paczka jest węższa.
Jeśli impuls rozchodzi się w ośrodku bezdyspersyjnym, to nie zmienia kształtu, ponieważ wszystkie fale z których jest zbudowany rozchodzą się z taką samą prędkością. Natomiast w ośrodku dyspersyjnym fale harmoniczne tworzące impuls rozchodzą z różnymi prędkościami i dlatego kształt impulsu ulega zmianie. Ten efekt prześledźmy na przykładzie ewolucji impulsu „gaussowskiego”, pokazanego na rysunku Figure 1 rozchodzącego się w ośrodku o zależności dyspersyjnej: [math]\omega=\omega_0+\alpha k^2\;[/math].
Przyjmijmy następujące warunki początkowe:
- [math]\Psi(z,0)=e^{-\frac{z^2}{2L^2}}\cos k_0z[/math],
- [math]\frac{\partial\Psi}{\partial t}(z,0)=0[/math].
Uwzględniając warunki początkowe znajdujemy:
- [math]c(k)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\Psi(z,0)e^{-ikz}\mathrm dz=\sqrt{2\pi}Le^{-\frac{L^2}{2}(k-k_0)^2}[/math],
a następnie postać biegnącego impulsu:
- [math]\Psi(z,t)=\int_{-\infty}^{+\infty}c(k)e^{i(kz-\omega(k)t)}\mathrm dk[/math]
- [math]A(z,t)=\frac L\sqrt\sigma e^{-\frac{(z-2\alpha k_0t)^2}{2\sigma^2}}[/math],
gdzie:
- [math]\sigma=\sqrt{L^2+\frac{2\sigma^2t^2}{L^2}}[/math].
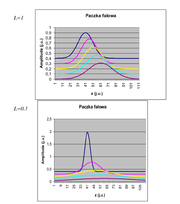
Na rysunku Figure 2 pokazano ewolucję impulsu dla dwóch wartości parametru L (czyli szerokości impulsu). Widać, że kształt impulsu ulega zmianie, przy czym wąski impuls szybko się „rozmywa”. Jest to związane z tym, ze wąski impuls zbudowany jest z bardzo szerokiego widma fal harmonicznych. Fale te rozchodzą się z prędkościami z szerokiego zakresu, dlatego kształt impulsu szybko się zmienia.
Dla paczek falowych rozchodzących się w ośrodkach dyspersyjnych wprowadza się dwa rodzaje prędkości:
- Prędkość fazową: [math]v_f=\frac \omega k[/math]. Wielkość ta opisuje prędkość rozchodzenia się punktów stałej fazy.
- Prędkość grupową zdefiniowaną: [math]v_g=\frac{\mathrm d\omega}{\mathrm dk}[/math]. Wielkość ta opisuje prędkość punktów stałej amplitudy (a więc prędkość środka ciężkości paczki falowej).
W ogólnym przypadku prędkość grupowa może być większa, równa lub mniejsza w stosunku do prędkości fazowej. W ośrodku bezdyspersyjnym: [math]v_f=v_g\;[/math].