Fizyka III/Współczynnik załamania dielektryka i przewodnika

W obszarze widmowym długich fal współczynnik załamania silnie zależy od częstości, np. dla wody n zmienia się od około 1,33 (światło sodowe [math]\lambda=\unit{589}{nm}[/math]) aż do około 9 dla [math]\lambda=\unit{3}{m}[/math] . Tak dużą zmianę współczynnika załamania z częstością można wyjaśnić następującym bardzo prostym modelem oscylatora. Model ten opiera się na następujących założeniach:

• ośrodek wypełniony jest jednorodnie atomami, N atomów w jednostce objętości,
• jądra atomowe są nieruchome,
• chmura elektronowa opisana jest przez ładunek q i masę m,
• na ładunek działa siła harmoniczna: [math]\vec F_\mathrm h = -m\omega_0^2\vec r[/math] oraz bardzo mała siła tłumiąca (powoduje, że rozpatrujemy tylko rozwiązanie stacjonarne oscylatora tłumionego), na tyle mała, że w rozwiązaniu stacjonarnym pomijamy tłumienie,
• w ośrodku rozchodzi się fala elektromagnetyczna o długości dużo większej od rozmiarów atomów. Pole elektryczne fali powoduje ruch chmury elektronowej. Falę tę traktujemy jako siłę wymuszającą: [math]\vec F_\mathrm{wym} = q\vec E_0\cos\omega t[/math].

Chmura elektronowa wykonuje drgania opisane znanym nam równaniem oscylatora wymuszonego:

[math]\ddot \vec r +\omega_0^2\vec r =\frac{q\vec E_0}m\cos\omega t[/math],

którego rozwiązanie stacjonarne jest postaci:

[math]\vec r =\frac{q\vec E_0}{m(\omega_0^2-\omega^2)}\cos\omega t[/math].

Stąd otrzymujemy gęstość wyidukowanego prądu:

[math]\vec j =Nq\vec v =\frac{q^2N}{m(\omega_0^2-\omega^2)}\frac{\partial\vec E}{\partial t}[/math].

Tę gęstość prądu wstawiamy do równań Maxwella:

[math]\mathrm{rot}\ \mathrm{rot}\vec E = \mathrm{grad}\ \mathrm{div}\vec E-\Delta \vec E = -\varepsilon_0\mu_0 \frac{\partial^2\vec E}{\partial t^2}-\mu_0 \frac{\partial\vec j}{\partial t}[/math]

i otrzymujemy następujące równanie falowe:

[math]\Delta \vec E = \varepsilon_0\mu_0 \left(1+\frac{q^2N}{m \varepsilon_0(\omega_0^2-\omega^2)} \right)\frac{\partial^2\vec E}{\partial t^2}[/math].

Jest to klasyczne równanie falowe z przenikalnością elektryczną (a więc i współczynnikiem załamania) zależną od częstości:

[math]\varepsilon(\omega)= 1+\frac{q^2N}{m \varepsilon_0(\omega_0^2-\omega^2)}[/math]

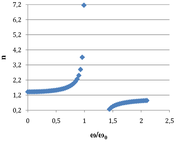
[math]n(\omega)=\sqrt{1+\frac{q^2N}{m \varepsilon_0(\omega_0^2-\omega^2)}}[/math].

W tym prostym modelu otrzymaliśmy zależność współczynnika załamania od częstości. Zależność ta jest bardzo silna w pobliżu częstości własnej oscylatora swobodnego (częstości własnej ośrodka). Na rysunku Figure 1 pokazano tę zależność, która mimo prostoty dość dobrze opisuje rzeczywiste zależności.

Przykładowa zależność współczynnika załamania od częstości w pobliżu częstości własnej oscylatora.

W prosty sposób rozpatrywany model możemy zastosować do przewodnika. W przewodniku mamy dużą liczbę swobodnych ładunków. Przejście do przewodnika polega na [math]\omega_0\rightarrow 0,\ 1\rightarrow\varepsilon_\infty[/math] (uwzględniamy w ten sposób ładunki swobodne oraz ładunki związane w zamkniętych powłokach). Otrzymujemy wówczas wzór na przenikalność elektryczną:

[math]\varepsilon(\omega)= \varepsilon_\infty-\frac{q^2N}{m \varepsilon_0\omega^2}=\varepsilon_\infty\left(1-\frac{\omega_p^2}{\omega^2}\right)[/math],

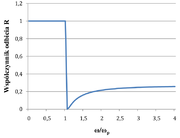
gdzie wprowadziliśmy oznaczenie: [math]\omega_p=\sqrt{\frac{q^2N}{m\varepsilon_0\varepsilon_\infty}}[/math]. Wielkość tę nazywamy częstością plazmową. Dla częstości mniejszych od częstości plazmowej [math]\varepsilon(\omega)\lt 0[/math], co oznacza, że współczynnik załamania jest urojony, a to z kolei oznacza, że współczynnik odbicia dla tego zakresu wynosi 1, a więc fale elektromagnetyczne o częstościach mniejszych są całkowicie odbijane od przewodnika. Dlatego metale odbijają światło, np. dla srebra odbijane są fale z całego zakresu światła widzialnego, natomiast dla złota częstość plazmowa wypada przy kolorze zielonym, stąd złoto „świeci” się na żółto.

Na rysunku Figure 2 pokazano współczynnik odbicia dla przewodnika.

Kształt współczynnik odbicia dla przewodnika (według wzorów omawianych w tekście).